5.2 対応ありt検定

今度は対応ありt検定について見ていきましょう。対応ありt検定は，2種類の測定値の間に明確なペアが存在する場合に，その母集団の平均値に統計的な差があるといえるかどうかを確かめるのに使用されます（図5.19）。

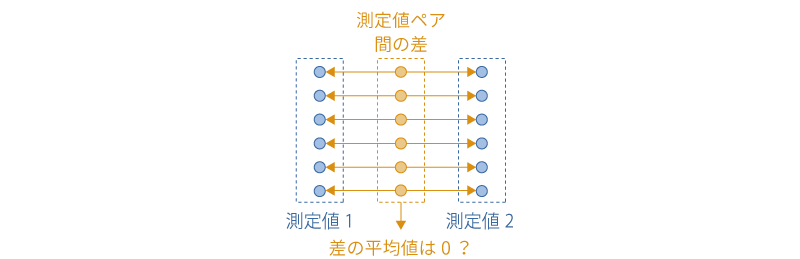
図5.19: 対応ありt検定

この検定が用いられる典型的な場面は，ある処置を行う前後で平均値に差があるかどうかを確かめるというものです。この場合，それぞれの対象者について処置前と処置後の2回の測定を行いますので，同じ対象者の測定値同士で前後の比較を行うことができます。このように，2つのグループ（処置前と処置後）の測定値の間で特定のペアが成立するデータを一般に「対応ありデータ」と呼びます。

5.2.1 考え方

対応なしのt検定の場合と異なり，対応ありのt検定では対象者ごとに2つの条件における測定値の差を求め，その「測定値の差の平均値」を用いて検定を行います。2つの条件（処置前と処置後など）に違いがなければ，どちらの条件の測定値も同じような値になるはずで，その場合，2条件の測定値の差の平均値は0に近い値になります。このような考えから，対応ありt検定では，2条件の測定値の差の平均値が0であるといえるかどうかを確かめます。

5.2.2 分析手順

ここでは次のサンプルデータ（ttests_data02.omv）を用いて対応ありt検定の実施方法を見ていきましょう。このデータは，20名の参加者を対象に，効率的な記憶法の訓練前と訓練後における記憶課題の成績を測定したものです。このデータファイルには，次の3つの変数値が格納されています（図5.20）。

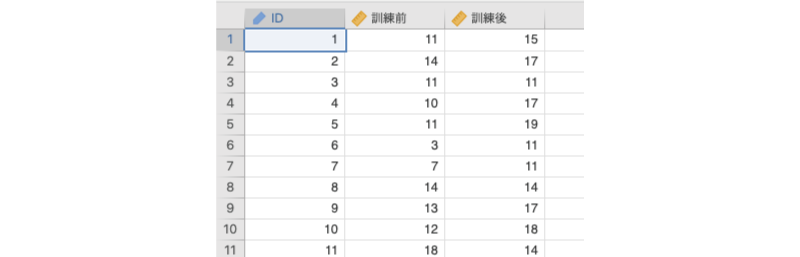
図5.20: サンプルデータ

ID　対象者のID
訓練前　訓練前の記憶課題成績
訓練後　訓練後の記憶課題成績

それでは，訓練前と訓練後で，記憶課題成績の平均値に差があるといえるかどうかを検定してみましょう。対応ありt検定を行うには，分析タブの「 inline t検定」から「対応ありt検定」を選択します（図5.21）。

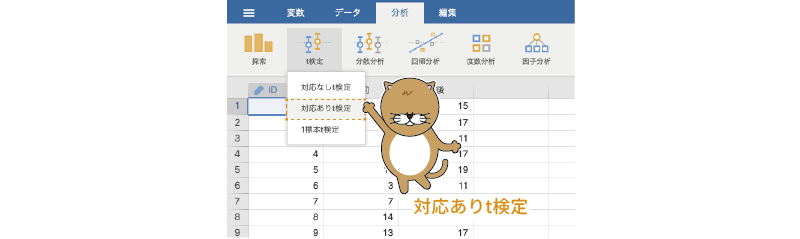
図5.21: 対応ありt検定の実行

すると，図5.22のような画面が表示されます。設定項目がたくさんありますが，そのほとんどは対応なしt検定の場合と同じです。

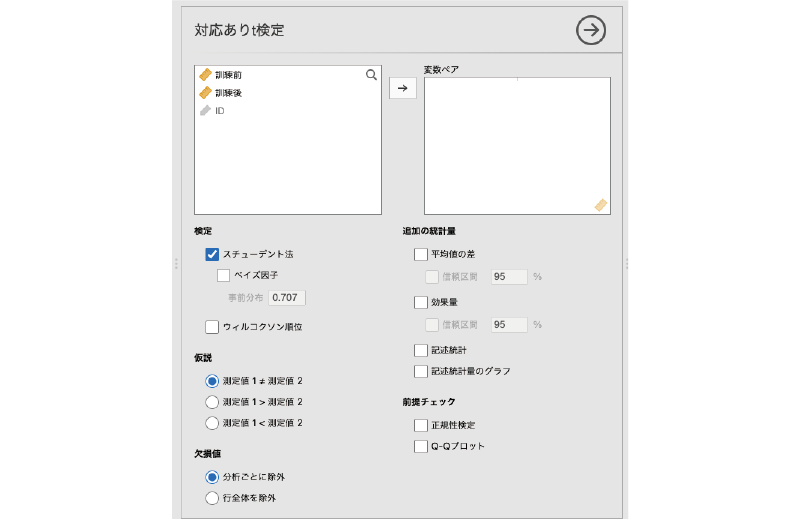
図5.22: 対応ありt検定の分析設定画面

変数ペア　分析対象の変数ペアを指定します
検定　分析に用いる検定を指定します
仮説　検定に用いる仮説を選択します
欠損値　データに欠損値が含まれている場合の対処方法を指定します
追加の統計量　一般的な分析結果に加えて算出したい統計量を指定します
前提チェック　検定に必要な前提条件が満たされているかどうかの確認を行います

この分析で必ず設定する必要がある項目は「変数ペア」のみです。変数ペアには，分析対象となる変数のペアを指定します。サンプルデータの場合，「訓練前」と「訓練後」の差について検定したいので，この2つを「変数ペア」欄に移動します。

このとき，「訓練前」と「訓練後」を1つずつ「変数ペア」欄に移動することもできますが，2つまとめて移動させる方がわかりやすいでしょう。まずどちらか一方の変数名をクリックして選択した後，「SHIFT(⇧)」キーを押しながらもう一方の変数名をクリックすると2つの変数を同時に選択することができますので，その状態で「 inline 」をクリックして変数ペアの設定を行います（図5.23）。

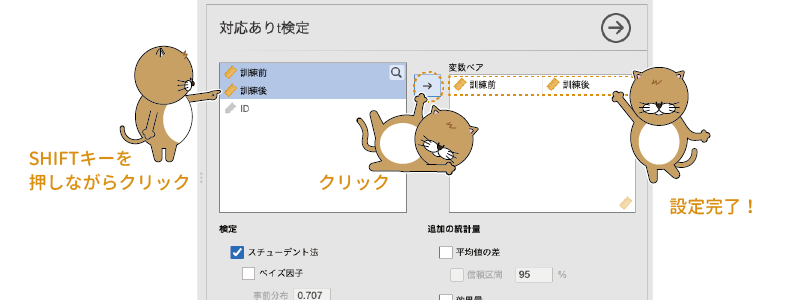
図5.23: 変数ペアの設定

対応なしt検定の場合と同様に，この設定だけで基本的な分析結果が得られます（図5.24）。

図5.24: 対応ありt検定の分析結果

変数名の代わりに変数ペアが表示されること以外は，分析結果の表も対応なしt検定の場合と同じです。この分析結果では，有意確率pの値が「<.001（0.001未満）」となっていますので，検定結果は有意，つまり記憶法の訓練前後で平均値に有意な差があるということになります。

なお，検定統計量は変数ペアの左側の変数から右側の変数の値を引いて算出されています（サンプルデータの場合は「訓練前 − 訓練後」）。両側検定の場合，検定結果が有意かどうかは統計量の絶対値で判断しますので問題ありませんが，片側検定の場合，この統計量がどちらからどちらを引いた値に基づくものであるのかに注意が必要になります。

この分析の設定項目は，「検定」の部分を除いて対応なしt検定の場合と同じです。重複する部分については説明を省略します。

検定

対応ありt検定の「検定」には，次の項目が含まれています（図5.25）。

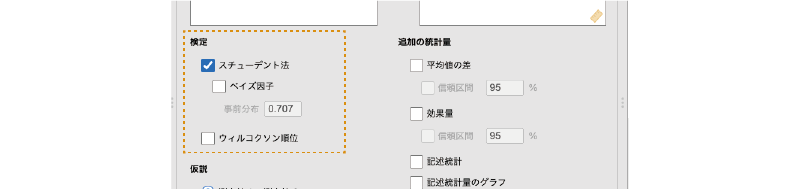
図5.25: Test（検定）の設定項目

スチューデント法　スチューデントの検定による検定結果を表示します。
- ベイズ因子　帰無仮説と対立仮説の間でベイズ因子を算出します。
ウィルコクソン符号順位検定　ウィルコクソン符号順位検定（Wilcoxon符号順位検定）の結果を表示します。

「検定」の項目もほとんどは対応なしのt検定と同じですが，対応ありt検定の場合，t検定の計算方法はスチューデントの検定のみになります。また，この場合のノンパラメトリック検定には，ウィルコクソン符号順位検定と呼ばれる検定手法が用いられます。

それ以外の項目は，すべて対応ありt検定の場合と同じですので，詳細については対応なしt検定のところを参照してください。

なお，スチューデントの検定について「追加の統計量」で効果量を算出した場合は，対応なしt検定の場合と同様にコーエンのdが，ウィルコクソン符号順位検定について効果量を算出した場合，マン=ホイットニーの検定の場合と同様に順位双列相関係数が表示されます。