6.4 共分散分析

たとえば記憶課題を用いた実験を行う場合，その記憶課題の成績は，実験で操作される条件以外に各参加者の記憶力の違いによっても影響を受けるかもしれません。あるいは，食行動に関する研究では，観察対象である食行動がそれぞれの参加者の体格によって異なるかもしれません。一般に，このような場合には，実験の各条件で参加者の特性に偏りが生じないように，あらかじめ測定した記憶力や，体格指標などにもとづいて参加者を各条件に振り分けるといった方法が用いられます。

ただ，たとえばもともと記憶力のいい人ほど課題成績がよく，そうでない人ほど課題成績が低いというような関係があった場合，それぞれの条件に参加者を均等に振り分けるというような方法では，参加者個人の記憶力の差や体格の差を十分にコントロールすることはできません。そのままでは，参加者個人の記憶力の違いによって，各実験条件における課題成績のばらつきが大きくなり，実際には実験条件の効果があるにもかかわらず，それを検出できないということが起こり得ます。

共分散分析（ANCOVA）は，この各参加者の記憶力の違いのように，本来測定したい値に対して系統的に影響を与えるような変数がある場合に，その変数の影響を取り除いたうえで，実験要因の影響について検討したい場合に用いられる分析手法です。

6.4.1 考え方

ここでは次の実験データについて考えてみましょう。勉強中のBGMが勉強効率にどのように影響するのかを調べるため，参加者75名をBGMなし，音楽のみのBGM，歌詞ありのBGMの3つの条件に25名ずつに振り分けて記憶課題を実施しました。記憶課題は，無意味つづり30個が記載されたリストを記憶し，その後，それらの無意味つづりを再生するというものです。なお，参加者を3つの条件に振り分ける際には，作業記憶容量の測定課題を実施し，各条件でその点数ができるだけ均等になるようにしました。次のサンプルデータ（anova_data04.omv）には，この実験の結果が入力されています（図6.66）⁷。

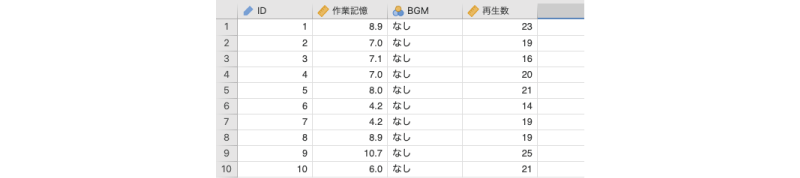
図6.66: サンプルデータ

• ID　実験参加者のID
• 作業記憶　実験参加者の作業記憶の容量
• BGM　学習時のBGM（なし，音楽のみ，歌詞あり）
• 再生数　無意味つづりの再生数

まず，3つの条件で参加者の作業記憶の容量に偏りがないかどうかを確認してみましょう。分析タブの「 探索」から「記述統計」を選択し，「作業記憶」のBGM条件ごとの平均値と標準偏差を算出します。このとき，結果の表示方法を「行に変数を配置」に設定しておくと結果が見やすくなります。

図6.67: 作業記憶容量の記述統計

実行結果は，図6.68のようになりました。

図6.68: 作業記憶容量の平均値と標準偏差

どの条件も作業記憶容量の平均値は約7.0，標準偏差は1.7から1.8で，だいたい同じような値になっています。各条件への参加者の振り分けは，狙いどおりに均等になっているようです。

次に，作業記憶の容量と記憶課題における再生数の間に相関関係があるかどうかを見てみましょう。ここで両者に相関がないようであれば，共分散分析を用いても意味がありません。

「 回帰」から「相関行列」を選択し，「作業記憶」と「再生数」の2つを指定してこの2つの間の相関係数を算出します（図6.69）。「 回帰」ツールや相関係数の算出方法についての詳細は，第7章の「回帰分析」を参照してください。

図6.69: 相関係数の算出

結果を見てみると，「作業記憶」と「再生数」の間の相関係数は0.62で，やや強めの正の相関があります（図6.70）。つまりこれは，作業記憶の容量が多い人ほど，再生数が多いという関係があるということです。このように，分析における従属変数（再生数）に対して系統的な影響を与える変数（作業記憶の容量）のことを共変量と呼びます。

図6.70: 「作業記憶」と「再生数」の相関係数

さて，作業記憶の容量が無意味つづりの再生数に影響するということは，各条件における無意味つづりの再生数には作業記憶容量の個人差によるばらつきが生じるということになります。参加者個人の特性の違いによって測定値にばらつきが生じるのはどんな実験の場合でも同じでしょうが，今回の実験ではそのばらつきの主な原因である作業記憶の容量についての測定値がありますので，これを利用しない手はありません。

このとき，共分散分析では，まず「線形回帰（第7章）」を用いて，共変量（作業記憶容量）から従属変数（再生数）のばらつきを説明するモデルを作成します。そして，このモデルによる予測値とのずれ（残差）を用いて分散分析を行うのです。このようにすると，「作業記憶」と「再生数」の相関関係による影響を取り除いた形で分析を行うことができます。

この考え方を図で示すと図6.71のようになります。

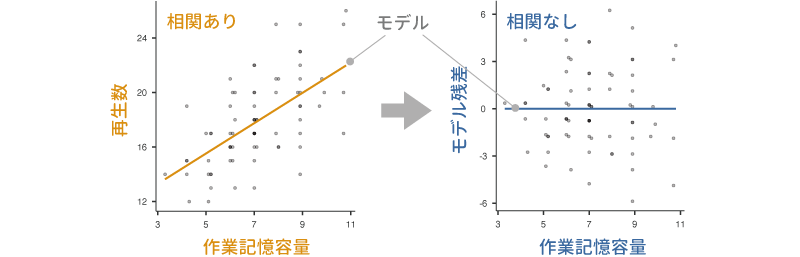
図6.71: 「作業記憶」による「再生数」への影響の除去

図6.71の左側の図は，作業記憶の容量を横軸に，再生数を縦軸にとって作成した散布図です。この散布図では，全体が右肩上がりになっており，正の相関があるということが視覚的にもよくわかります。そして，この散布図の中央にある斜めの線が，作業記憶の容量と再生数の関係を表したモデルです。

これに対し，右側の図は横軸に作業記憶の容量を，縦軸には左の図に直線で示したモデルからのずれ（残差）をとって作成した散布図です。こちらの図では，モデルで示される関係が水平な直線になっていることからもわかるように，作業記憶の容量と残差の間に相関関係は見られません。

このように，実験条件以外で従属変数に影響を与えていると考えられる共変量がある場合，その共変量で従属変数を説明するモデルを作成し，そこからのずれを求めるという方法をとると，その共変量による従属変数への影響を取り去ることができるのです。共分散分析では，このようにして従属変数の値から共変量による影響を取り除き，そのうえで実験条件の主効果や交互作用があるといえるかどうかについて検定を行います。

6.4.2 分析手順

共分散分析は，分析タブの「 分散分析」から「共分散分析」を選択して実施します（図6.72）。

図6.72: 共分散分析の実行

すると，次のように「分散分析」と非常によく似た設定画面が表示されます（図6.73）。

図6.73: 共分散分析の設定画面

実際，「分散分析」の設定画面との違いは，「固定因子」の下に「共変量」の指定欄があるかどうかだけです。

そして，分析手順もほぼ「分散分析」と同じです。「従属変数」に「再生数」を，「固定因子」に「BGM」を入れます。ここまでは「分散分析」の場合と同じです。違うのは，「共変量」に「作業記憶」を指定することだけです（図6.74）。

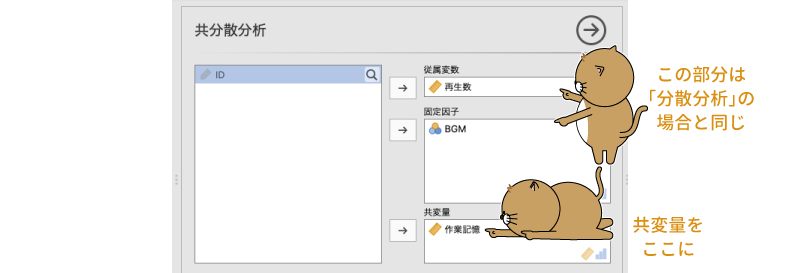
図6.74: 共分散分析の分析設定

これで基本の分析設定はおしまいです。

6.4.3 分析結果

共分散分析の結果は，図6.75のような形で表示されます。

図6.75: 共分散分析の結果

分析方法だけでなく，結果の表示も「分散分析」の場合とほとんど同じです。この結果の表の「BGM」の行がBGMの主効果についての検定結果です。この分析結果ではp=0.017ですので，5%水準の検定であればBGMの主効果は有意ということになります。

結果の表の2行目にある「作業記憶」の部分は，作業記憶の容量という共変量による再生数への影響についての検定結果です。この検定結果では，作業記憶の容量による影響も有意になっています。では，もし今回のデータで共変量を用いずに分析した場合，結果はどのようになるのでしょうか。

それを確かめるために，設定画面で「共変量」から「作業記憶」を外してみてください。すると，結果は図6.76のようになります。

図6.76: 共変量を用いない場合の分析結果

「BGM」の有意確率がp=0.088となり，主効果が有意でなくなりました。なお，この結果は，共変量を用いない共分散分析，つまり分散分析の結果と同じです。実際，この結果は，「分散分析」で「再生数」を従属変数，「BGM」を固定因子に設定して分析した場合と同一です。

つまり，今回の実験の場合，もし参加者の作業記憶の容量が測定されておらず，BGMの違いだけを用いて分析していたとしたら，BGMの違いによる記憶再生量への影響は見過ごされてしまっていた可能性があるのです。

さて，先ほどから何度も繰り返しているように，この「共分散分析」の設定項目は，共変量の設定欄がある以外は「分散分析」のものと同一です。そのため，| モデルや| 前提チェックなどの設定についての個別の説明はここでは省略します。それらについては「分散分析」の該当箇所を参照してください。

なお，「反復測定分散分析」の分析設定画面にも「共変量」という設定欄があったのを覚えているでしょうか。じつは，「反復測定分散分析」では共変量を用いた分析も可能で，その際の共変量についての考え方は，この共分散分析の場合と同じです。つまり，「反復測定分散分析」のメニューでは，反復測定分散分析と反復測定共分散分析の両方が可能ということです。

最後に，せっかくですのでBGMの主効果について多重比較と推定周辺平均の算出を行っておきましょう。さきほど「作業記憶」を共変量から外した人は，この変数を共変量に設定しなおしたことを確認してから，多重比較を行なってください。図6.77は，| 事後検定で「BGM」の各水準間の差について「テューキー」法による多重比較を行った結果です。

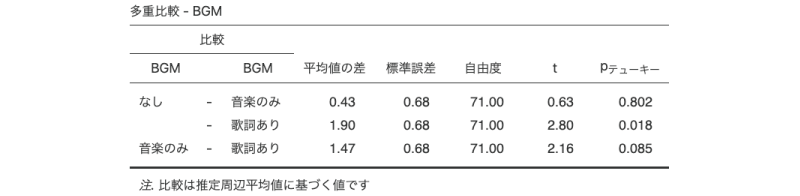
図6.77: BGMの主効果についての多重比較

多重比較の結果では，「なし」と「歌詞あり」の水準間に有意な差がみられました。共変量（作業記憶）の影響を取り除いたあとの「なし」と「歌詞あり」の平均値の差は1.90で，「なし」のほうが「歌詞あり」よりも平均値が大きいですので，「なし」のほうが「歌詞あり」に比べて有意に記憶成績が高いということになります。また，BGM要因の各水準における推定周辺平均値をグラフに示したものが図6.78です。この図を作成するには，| 推定周辺平均で「項」に「BGM」を設定してください。

多重比較のところで見たように，「なし」は「歌詞あり」より平均再生数が多くなっています。また，多重比較では統計的に有意な差は見られませんでしたが，この図を見る限りでは，「歌詞あり」の条件は「音楽のみ」の条件に比べても記憶成績が悪くなっています。これらの結果をまとめると，どうやら勉強中のBGMとして歌詞つきの音楽を使うのは，記憶成績が悪くなる（勉強効率が落ちる）ため，避けた方がよさそうだということになります。

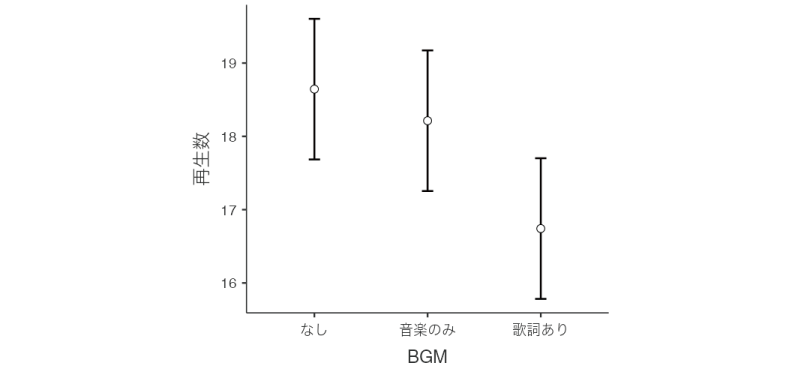
図6.78: BGMの各水準における推定周辺平均値と95％信頼区間

---

7. Windows版のjamoviでは，変数名に日本語が含まれている際に正しく分析できません。以下の内容は，サンプルデータの変数名を英数字に変更したうえで実行してください。↩︎