6.7 反復測定分散分析[フリードマン]
繰り返しなし(対応なし)の場合の1要因分散分析に対応するノンパラメトリック検定としてはクラスカル=ウォリス検定がありますが,1要因の反復測定分散分析に対応するノンパラメトリック検定にはフリードマン検定があります。
6.7.1 考え方
ここでは,次のサンプルデータ(anova_data06.omv)を用いて,フリードマン検定の基本的な考え方を見ておきましょう。このデータには,空間についての記憶実験の成績が記録されています。この実験では,模型の観察(模型条件),VRによるインタラクティブな空間体験(VR条件),あらかじめ録画された動画視聴による空間体験(動画条件)の3つの条件それぞれで架空の都市空間を体験してもらい,その後,その空間にあった建物の位置や形などについての記憶テストを行いました(図6.107)。記憶課題の成績は,数値が大きいほど好成績であることを意味します。
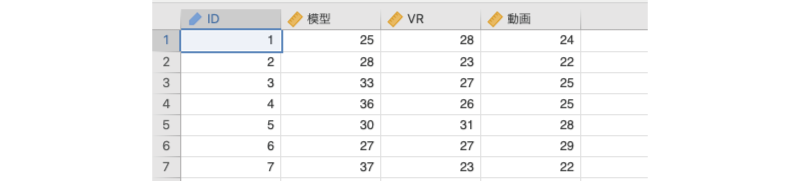
図6.107: サンプルデータ
ID実験参加者のID模型模型観察条件の課題成績VRVR条件の課題成績動画動画条件の課題成績
フリードマン検定では,クラスカル=ウォリス検定の場合と同様に,測定値の順位を利用して条件間に差があるかどうかを検定します。ただし,クラスカル=ウォリス検定では各測定値にデータ全体での順位をつけ,それを各条件で平均するという方法を取りましたが,フリードマン検定の場合には,参加者ごとに各条件の測定値の順位づけを行います。
たとえば,今回のデータでは,1人目の参加者の課題成績は,「模型」条件が「25」,「VR」条件が「28」,「動画」条件が「24」ですので,この3つで順位をつけると,「模型:2,VR:3,動画:1」となります。このような形での順位づけをすべての参加者に対して行ったとき,3つの条件の間に明確な差がある(明確な順序がある)のであれば,この順位づけの値はどの参加者でも同じになるはずです。そしてもし,そのように参加者間で順位が一致しているのであれば,3つの条件それぞれで全参加者の順位づけの値を合計したとき,その合計値は3つの条件で大きく異なる値になるでしょう。
しかし,この3つの条件に差がなく,順序がはっきりしなければ,それぞれの参加者における順位づけの値は,参加者ごとにまちまちになります。すると,3つの条件それぞれで全参加者の順位づけの値を合計したとき,3つの条件の順位の合計値に違いは見られなくなります。
このような考え方から,フリードマン検定では,各参加者における測定値の順位を測定条件ごとに集計することで,各参加者の測定値の順位が一致している程度を調べ,その情報をもとに,条件間に差があるかどうかの判断を行います。
6.7.2 分析手順
フリードマン検定の実行には,分析タブの「 分散分析」で,「ノンパラメトリック」の部分にある「反復測定分散分析[フリードマン]」を選択します(図6.108)。分析メニューに「反復測定分散分析」とあるのは,この分析が反復測定分散分析のノンパラメトリック版に相当するものだからです。
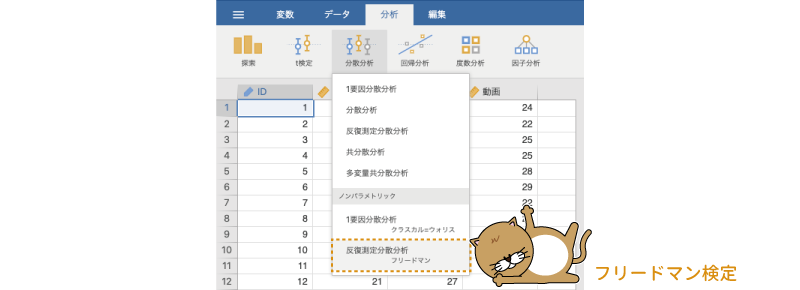
図6.108: フリードマン検定の実行
このメニューを選択して実行すると,図6.109のような設定画面が表示されます。こちらも非常にシンプルなものです。
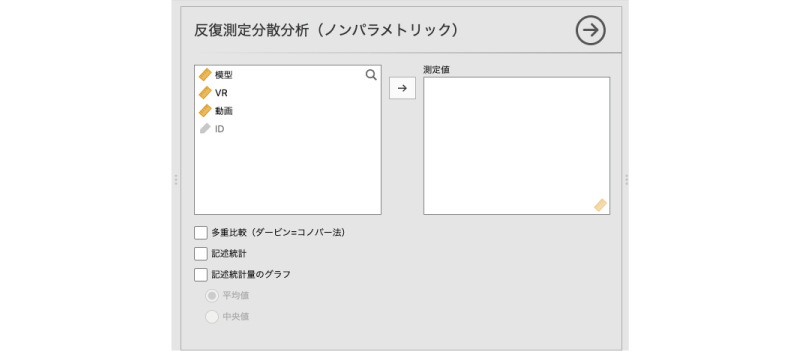
図6.109: フリードマン検定の設定画面
フリードマン検定の基本設定は,この設定画面で分析対象の変数すべてを「測定値」のところへ移動するだけで完了です(図6.110)。
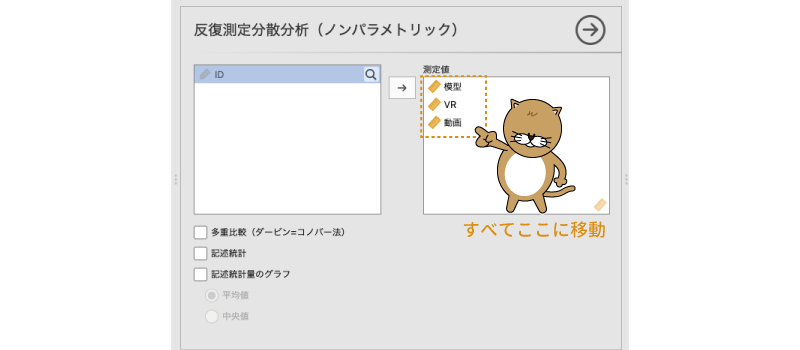
図6.110: フリードマン検定の分析設定
6.7.3 分析結果
それでは結果を見てみましょう。フリードマン検定の結果は図6.111のような形で表示されます。

図6.111: フリードマン検定の結果
結果の表に表示される項目はクラスカル=ウォリス検定の場合と同じで,\(\chi^2\)統計量と自由度,そしてp値です。この検定でも\(\chi^2\)の値を用いて検定を行います。この検定の帰無仮説は「すべての条件で分布が同じ」なので,この検定結果の有意確率が有意水準を下回る場合に「すべての条件で分布が同じでない(分布に差がある)」ということになります。今回の分析結果ではp=0.001なので,条件間の差は有意です。
6.7.4 多重比較と記述統計量
フリードマン検定では,基本設定以外の設定項目は多重比較と記述統計量の算出に関するものだけです。
多重比較(ダービン=コノバー法)
jamoviのフリードマン検定には,多重比較の方法としてダービン=コノバー法と呼ばれる手法が用意されています。設定画面の「多重比較(ダービン=コノバー法)」にチェックを入れると,図6.112のような形で多重比較の結果が表示されます。

図6.112: フリードマン検定後の多重比較
結果の表には「統計量」としか書かれていませんが,この値はスチューデントのtの推定値で,その隣の「p」の欄はこのtの有意確率です。なお,DSCF法の場合とは異なり,このp値には多重比較の際の調整が加えられていませんので,実際の検定場面では,このp値をボンフェロニ法やホルム法で修正してから判断したほうがよいでしょう。
この結果のp値をボンフェロニ法で修正する場合,今回は多重比較を全部で3回行っていますので,p値をすべて3倍して判断することになります。すると,「模型」条件と「動画」条件(p<.001 × 3 <0.003),「VR」条件と「動画」条件(p=0.004 × 3 =0.012)の間の差が有意ということになります。
記述統計
2つ目の「記述統計」の項目は,その名のとおり各条件における記述統計量を算出するための設定項目です。ここにチェックを入れると,各条件における測定値の平均値と中央値が表示されます(図6.113)。

図6.113: 各条件の平均値と中央値
記述統計量のグラフ
3つ目の「記述統計量のグラフ」にチェックを入れると,各条件の記述統計量をグラフに示すことができます。その際,下のラジオボタンで「平均値」を選択すると平均値のグラフが,「中央値」を選択すると中央値のグラフが作成されます(図6.114)。
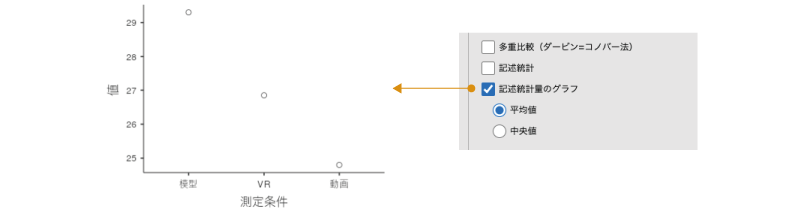
図6.114: 記述統計量のグラフ