7.4 2値従属変数[2項]
ある症状の有無に喫煙や飲酒といった生活習慣がどの程度影響を与えているのか,ある課題の成功・失敗に対象児の月齢や発達指数がどのように影響しているか,災害に対して備えをする・しないを規定する要因にはどのようなものがあるのか,など,何らかの出来事の「成功・失敗」や「あり・なし」と,その影響要因について検討したいということもあるでしょう。
その場合,関心対象となる出来事の有無(成功・失敗)を「1・0」などとダミーコード化して従属変数とし,原因として考えうる要因を予測変数とした回帰分析を行えばよさそうに思えます。しかし,一般的な線形回帰分析では,「1・0」のような2値変数を従属変数として用いることはできません。線形回帰分析では,回帰モデルの残差が正規分布であることが前提となっていますが,従属変数の値が1と0の2種類しかない場合,残差が正規分布であるということがまず考えられないからです。
そこでこのような場合には,ロジスティック回帰分析と呼ばれる手法がよく用いられます。この手法は,従属変数が名義型や順序型の変数である場合にも適切な結果が得られるように,線形回帰分析の考え方を拡張したものです。ロジスティック回帰分析には,従属変数が2値変数の場合に用いられる2項ロジスティック回帰分析,従属変数が複数のカテゴリーをもつ名義型変数である場合に用いられる多項ロジスティック回帰分析,従属変数が順序型変数である場合に用いられる順序ロジスティック回帰分析など,いくつかの種類が存在します。
ここではまず,次のサンプルデータ(regression_data03.omv)を用いて,2項ロジスティック回帰分析についての基本的な考え方と分析方法を見ていくことにしましょう。
このデータファイルには,ある災害を体験した成人100名について,PTSD(心的外傷後ストレス障害)の有無とその人の性別と年齢,神経症傾向の強さ,そして体験した出来事の主観的強度が記録されています(図7.67)。
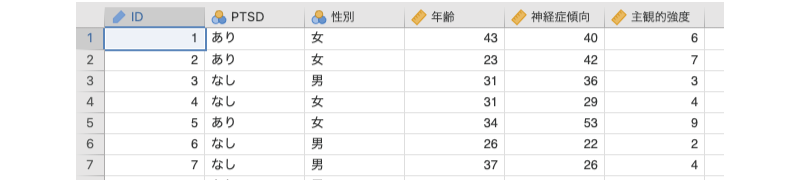
図7.67: サンプルデータ
ID対象者のIDPTSDPTSDの有無(あり,なし)性別対象者の性別(男,女)年齢対象者の年齢神経症傾向対象者の神経症傾向の強さ(5〜65点)主観的強度体験の主観的強度(1〜10点)
このデータを用いて,PTSDの有無にどの要因がどのような影響を与えているのかを分析することにしましょう。
7.4.1 考え方
PTSDの有無に性別や年齢などがどのように影響を与えているかを見たい場合,その分析モデルを回帰式の形で表すと次のようになります。なお,分析においてはPTSDの有無は「あり」を「1」,「なし」を「0」としてダミーコード化するものとします。また,予測変数に含まれる性別についてもダミーコード化されているものとします。
\[ \text{PTSDの有無} = b_0 + b_1 \times \text{性別} + b_2 \times \text{年齢}+ b_3 \times \text{神経症傾向}+ b_4 \times \text{体験強度} \]
通常の回帰分析では,従属変数は連続型変数である必要がありますが,このモデルでは従属変数に相当する「PTSD」には「1(あり)」か「0(なし)」かのいずれかの値しかありません。そのため,適切な分析結果を得るには,従属変数である「PTSDの有無」を何らかの形で連続的な数値に変換する必要があります。
ではたとえば,従属変数にPTSDの有無そのものではなく,PTSDが「あり」である確率を用いたらどうでしょうか。これならば,従属変数の値は0から1までの連続的な値をとり得ますし,そして算出された確率値が0.5以上なら「あり」,そうでなければ「なし」のように判断すれば,従属変数が2値データであってもうまく扱えそうです(図7.68)。
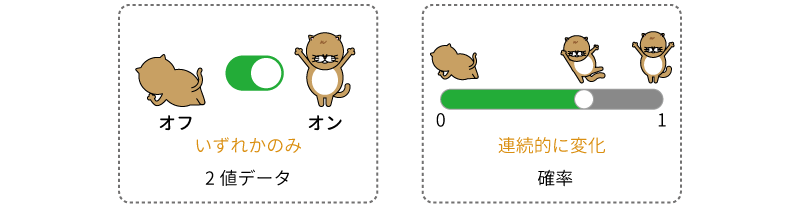
図7.68: 2値データと確率
一見するとこれで問題が解決したかのように見えるのですが,残念ながらこれでもまだ不十分です。というのも,確率の値がとるのは0から1までの範囲に限られていて,回帰式ではそのような範囲を限定した予測はできないからです。そのため,回帰式による予測値がマイナスの値になったり1を超えるような値になったりした場合には,その結果を解釈することができなくなってしまいます。
そこでその対策として,まず従属変数の値を確率からオッズへと変換します。オッズというのは,ある出来事が起きる場合と起きない場合のそれぞれの確率の比のことで,たとえば「PTSDあり」の場合のオッズは次のようにして求められます。
\[ \text{PTSDありのオッズ} = \frac{\text{PTSDありの確率}}{\text{PTSDなしの確率}} = \frac{\text{PTSDありの確率}}{1-\text{PTSDありの確率}} \]
もし「PTSDあり」が20人に1人の割合だったとすると,無作為に選ばれたある個人が「PTSDあり」である確率は「1/20 = 0.05」ですから,この場合の「PTSDあり」のオッズは次のようになります。
\[ \text{PTSDありのオッズ} = \frac{0.05}{1-0.05} = 0.0526\dots \]
また,「PTSDなし」であるオッズを算出したいなら次のようになります。
\[\begin{eqnarray*} \textsf{PTSDなしのオッズ} & = & \frac{\text{PTSDなしの確率}}{\text{PTSDありの確率}} = \frac{\text{PTSDなしの確率}}{1-\text{PTSDなしの確率}}\\ & = & \frac{0.95}{1-0.95} = 19 \end{eqnarray*}\]
このようにして確率をオッズに変換することにより,従属変数の値は0から無限大の範囲をとることができるようになります。
ただし,PTSDありの確率がPTSDなしの確率よりも低い場合,PTSDありのオッズは0〜1の値しかとらないのに対し,PTSDなしのオッズは1から無限大となって,PTSDありの場合となしの場合で数値のとりうる幅が大きく異なってしまいます。また,もし回帰分析の予測値がマイナスの値になってしまう場合には,確率を用いる場合と同様に,結果を解釈できなくなってしまいます。
そこで,このオッズの値をさらに対数変換します。この「オッズの対数」のことを対数オッズあるいはロジットといい,「PTSDあり」の確率をpとしたときに,この確率pを次のようにして対数変換する式のことをロジット関数と呼びます。
\[ \text{PTSDあり(}p\text{)のロジット} = \log \left( \frac{p}{1-p}\right) \]
先ほどのPTSDありとなしの場合のそれぞれのオッズを対数変換すると,次のようになります。なお,この場合の対数には,一般にネイピア数e6を底とする自然対数が用いられます。
\[\begin{eqnarray*} \text{PTSDありのロジット} & = & \log \left( \frac{0.05}{1-0.05}\right) = -2.944\dots\\ \text{PTSDなしのロジット} & = & \log \left( \frac{0.95}{1-0.95}\right) = 2.944\dots \end{eqnarray*}\]
対数変換前のオッズの値では,同じ1/20の確率の現象について「あり」のほうに注目した場合と「なし」のほうに注目した場合とでまったく異なる値になりましたが,ロジットに変換すると,このように「あり」の場合と「なし」の場合で数値の符号が逆になるだけで絶対値は同じ,つまり,どちらの場合も値の幅は同じになるのです。
確率をオッズに,そしてオッズをロジットに変換することで,これでようやくPTSDの有無という2値変数を回帰分析の従属変数として用いることができるようになりました。ここから先は,通常の回帰分析の場合と同様です。予測変数から従属変数をできるだけうまく説明できるようにして,切片や回帰係数の値を算出します。
このように,2項ロジスティック回帰では,関心とする事象が生起する確率についてのロジットを従属変数に使用します。このことは結果の解釈においても重要な意味を持ちますが,それについては分析結果の見方のところで説明します。
7.4.2 分析手順
それではサンプルデータをロジスティック回帰で分析してみましょう。2項ロジスティック回帰を実行するには,分析タブの「 回帰分析」から「ロジスティック回帰」の下にある「2値従属変数[2項]」を選択します(図7.69)。
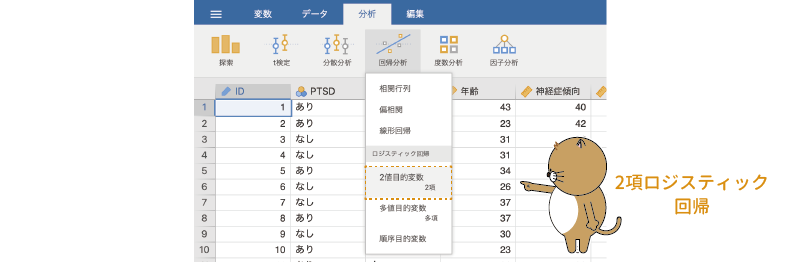
図7.69: 2項ロジスティック回帰の実行
すると,線形回帰分析の場合とよく似た設定画面が表示されます。最後から2つ目にという項目がある以外は線形回帰分析の設定画面と同じです(図7.70)。
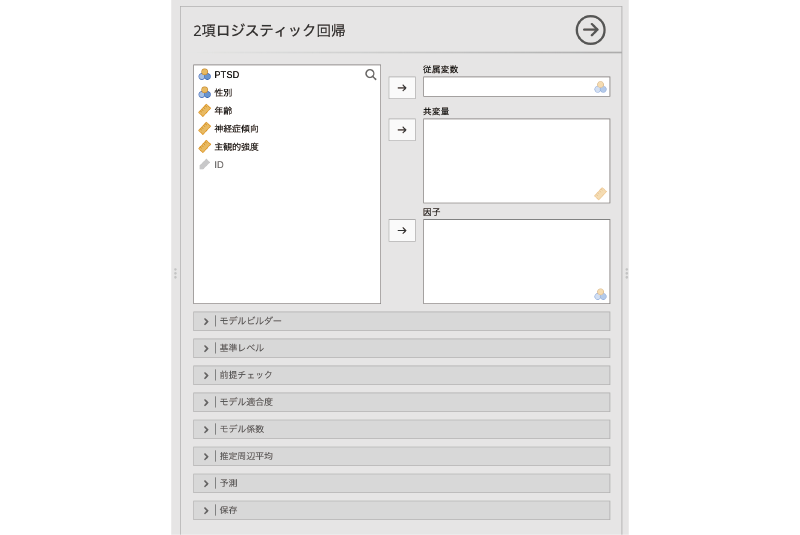
図7.70: 2項ロジスティック回帰の設定画面
表示された設定画面の「従属変数」に「PTSD」を,「共変量」に「年齢」,「神経症傾向」,「主観的強度」を,「因子」に「性別」を指定します(図7.71)。予測変数のうち連続型のものを「共変量」に,名義型のものを「因子」に設定するなど,変数の指定方法も線形回帰分析の場合と基本的に同じです。違うのは,従属変数(従属変数)に名義型変数()しか指定できないという点だけです。
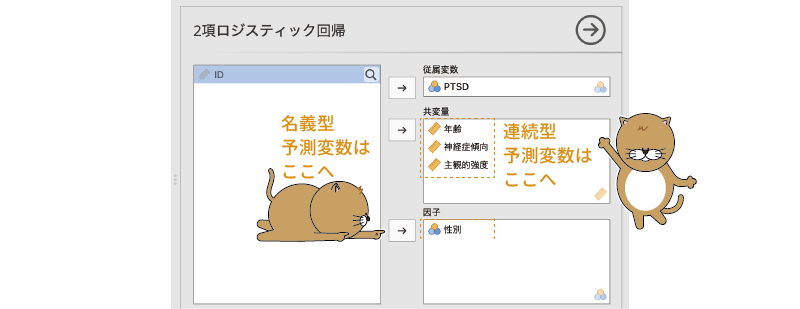
図7.71: 従属変数と予測変数の設定
これで基本的な設定は終わりですが,結果を見る前に1つだけ確認しておいたほうがよい部分があります。それは`の部分です(図7.72)。2項ロジスティック回帰では従属変数は「あり・なし」や「はい・いいえ」などの2値変数ですので,分析ではそれらのうちいずれか一方の値を基準とした結果が算出されます。2つの値のうちどちらが基準になっているのかによって結果の意味が逆になりますので,ここは必ず確認しておくようにしましょう。
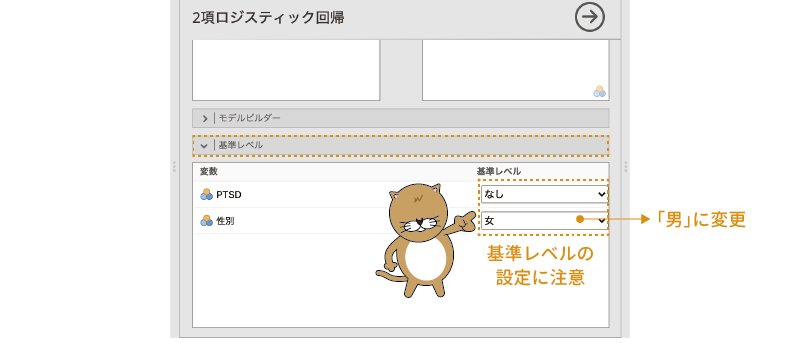
図7.72: 基準レベルの設定
またこのとき,2つの値のうちのどちらを基準として設定するかによって,結果のわかりやすさが大きく変わってきますので,その点にも注意してください。もし,分析によって各予測変数がPTSDの「なりやすさ」にどのような影響を与えているかを見たいのであれば,基準レベルには「なし」の値を設定するようにします。基準レベルが「あり」になっていると,分析結果にはPTSDの「なりにくさ」についての値が表示されてしまい,解釈が困難になってしまいます。
これは,予測変数に含まれる名義型変数についても同様です。線形回帰分析の場合,2つの値のどちらを基準にするかは,回帰係数の符号が逆になる程度でそれほど大きな違いはありません。しかし2項ロジスティック回帰では,従属変数の値は実際の測定値ではなく「はい」または「いいえ」が生じる確率の「ロジット」ですので,回帰係数の符号が逆になると解釈が非常に困難になってしまうのです。ですので,たとえば「『男性に比べて』女性のほうがどの程度PTSDになりやすいか」を見たいのであれば,性別の予測変数については「男性」を基準に,「『女性に比べて』男性がどの程度PTSDになりやすいか」を見たいのであれば,性別の予測変数は「女性」に設定しておいたほうがよいのです。ここでは,従属変数(PTSD)については「なし」を基準に,性別については「男性」を基準とした結果を算出することにします。
ここまでの設定が終わったら,分析結果を見てみましょう。図7.73のような結果が表示されているはずです。
7.4.3 分析結果
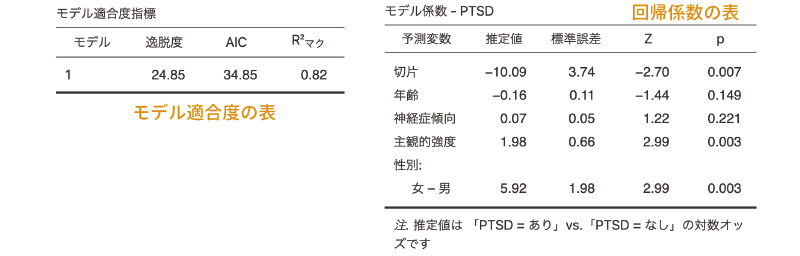
図7.73: 分析結果
1つ目(図7.73の左側)の表は,この回帰モデルの適合度指標に関する情報です。2項ロジスティック回帰では,初期設定では適合度の指標として逸脱度,AIC,\(\textsf{R}^{\textsf{2}}_{\textsf{マク}}\)(マクファデンのR²)の3つの値が表示されます。逸脱度およびAICは小さい値であるほど,R²の値は1に近い値ほど分析モデルのあてはまりがよいことを意味します。これらの適合度指標については,この後のの部分で説明します。
2つ目(図7.73の右側)の表は回帰係数に関する結果です。この部分は線形回帰分析の結果と基本的に同じで,「推定値」の部分が回帰係数,「標準誤差」が回帰係数の標準誤差です。ただし,2項ロジスティック回帰では,回帰係数の有意性についての検定にはtではなく「Z」が用いられます。そして,Zの隣の「p」の値が有意水準を下回っている場合に,回帰係数が有意である(0でない)と判断します。
この分析結果では,体験の主観的強度と対象者の性別の影響が有意で,それぞれの回帰係数は主観的強度が1.98,性別が5.92といずれもプラスの値です。つまり,体験の主観的強度が大きな値の人のほうが,また,男性よりも女性のほうが「PTSDあり」になりやすいということです。
このように,2項ロジスティック回帰の結果は線形回帰分析の場合と非常によく似ているのですが,注意すべき点が1つあります。それは,2項ロジスティック回帰の回帰式は,従属変数そのものについてではなく,従属変数の「ロジット」について説明する形になっているという点です。つまり,ここに示されている回帰係数は,予測変数の値が1変化した場合の,従属変数のロジットの変化量を表しているのです。
たとえば,この結果では性別(基準レベル = 男性)の回帰係数が5.92ですが,これは女性のほうが男性に比べて5.92倍PTSDになりやすい,あるいは5.92倍オッズが高いという意味ではなく,女性のほうが男性に比べて「PTSDあり」のロジットが5.92だけ増加するという意味になります。
ロジットはオッズを対数変換した値ですので,ロジットに対して対数変換の逆変換,つまり指数変換を行うことで,次のようにしてこの変化量をオッズに変換することができます。
\[ e^{5.92} = 372.4117\dots \]
この372.41という値は,男性を基準とした場合の女性のオッズの高さ,つまり男性のオッズと女性のオッズの比を表しており,女性の場合,男性に比べて「PTSDあり」であるオッズが372倍になるということを意味します7。この「女性のオッズ/男性のオッズ」のような,2つのオッズの比のことをオッズ比と呼びます。
先ほどは係数の値を指数変換することでオッズ比を求めましたが,実際にはこのような計算を自分でやる必要はありません。の設定画面で「オッズ比」の部分にチェックを入れれば,各回帰係数のオッズ比とその信頼区間を算出することができます。
なお,予測変数が連続型変数の場合,たとえばここでの分析結果では「主観的強度」は回帰係数が1.98で,これをオッズ比にすると7.21になります。これは,体験の主観的強度の値が1増えるとPTSDありのオッズが7.21場合になるということですが,ではもし,この体験の強度の値が2増えた場合,オッズ比はどうなるでしょうか。7.21 × 2 = 14.42倍でしょうか。そうではなく,この場合には\(7.21^2\) = 51.9841倍になります。
なぜそうなるのでしょうか。他の予測変数の値がすべて同じで,体験強度の値だけ異なる対象者が複数いたとしましょう。そのうちの1人(対象者A)は,体験の主観的強度の値が5で,もう1人(対象者B)は6だったとします。この場合,対象者AとBの体験強度の差は1ですから,先ほど見たように,対象者Bの「PTSDあり」のオッズは対象者Aの7.21倍になります。
さらに,体験強度が7の対象者(対象者C)がいたとしましょう。この対象者Cと先ほどの対象者Bの体験強度の差も1ですから,やはり対象者Cの「PTSDあり」のオッズは対象者Bの7.21倍になります。
するとこの場合,対象者Aと対象者Cの間には,体験の主観的強度の差が2だけあるわけですが,対象者Cは対象者Bの7.21倍のオッズで,そして対象者Bは対象者Aの7.21倍のオッズですから,対象者Cは対象者Aの7.21倍×7.21倍で51.9841倍になるのです。
実際の分析場面では,このようにして予測変数の値がいくつ増えたからオッズ比がどう,という形で結果を見ていくことはほとんどないかもしれませんが,結果の見方が線形回帰分析とまったく同じだと考えていると結果の解釈を誤ってしまう可能性もありますので,その点は注意しておきましょう。
少し長くなりましたが,これで結果の見方についての説明はおしまいです。ここからは,ロジスティック回帰分析の設定項目について見ていきましょう。なお,2項ロジスティック回帰の設定は大部分が線形回帰の場合と同じですので,ここでは2項ロジスティック回帰に特有の部分を中心に見ていくことにします。それ以外の部分については,線形回帰についての説明を参照してください。
7.4.4 前提チェック
2項ロジスティック回帰では,前提チェックの項目は「共線性統計量」の1つだけしかありません(図7.74)。線形回帰分析の場合にはいろいろあったのと対照的です。

図7.74: 前提チェック
ただし,では2項ロジスティック回帰は線形回帰よりも手軽に実行できるのかというと,そういうわけでもありません。今回のサンプルデータではそうではありませんが,実際のデータでは,「PTSDあり」の比率が「PTSDなし」に比べて非常に低いという場合もあるでしょう。そのような場合,「PTSDあり」の行がデータに十分に含まれていないと回帰係数をうまく推定できないのです。そのため,2項ロジスティック回帰には,一般に線形回帰分析よりも大きなサイズの標本が必要になります。
7.4.5 モデル適合度
分析結果のモデル適合度(Model Fit Measures)の表にどのような値を表示させるかは,分析設定画面ので設定できます(図7.75)。

図7.75: 適合度指標の設定
- 適合度指標
- 逸脱度 モデルの残差逸脱度を算出します。
- AIC 赤池情報量規準を算出します。
- BIC ベイズ情報量規準を算出します。
- モデル全体の検定 \(\chi^{2}\)を用いてモデル全体の有意性検定を行います。
- 擬似R² モデルのあてはまりの程度を標準化した値を算出します。
- マクファデンのR² マクファデン(McFadden)の擬似決定係数を算出します。
- コックス=スネルのR² コックス=スネル(Cox-Snell)の擬似決定係数を算出します。
- ナゲルケルケのR² ナゲルケルケ(Nagelkerke)の擬似決定係数を算出します。
適合度の指標に関する設定は,大きく「適合度指標」と「擬似R²」の2つに分かれています。ここでは,これらについて簡単に見ておきましょう。
適合度指標
「適合度指標」はその名のとおり,モデルの適合度(あてはまり)についての指標です。jamoviの2項ロジスティック回帰では,次の適合度指標を算出することができます。
逸脱度
1つ目の「逸脱度」にチェックを入れると,残差逸脱度が算出されます。残差逸脱度はモデルの尤度に基づいて算出される指標で,これは線形回帰分析における残差の2乗和に相当します。なお,線形回帰分析の係数は残差2乗和が最小になるようにして算出されますが,2項ロジスティック回帰ではこの逸脱度が最小になるようにして係数が算出されます。
なお,「尤度」とは,この分析モデルから手元のデータが得られる確率がどの程度あるか(モデルの尤もらしさ)を示した値です。残差逸脱度は,次のように分析モデルの尤度と完全モデル(実際のデータを完全に説明したモデル)の尤度の比を対数変換する形で求められます。
\[ \text{逸脱度} = -2\times\log \left(\frac{\text{分析モデルの尤度}}{\text{完全モデルの尤度}}\right) \]
この残差逸脱度の値が小さいほど,モデルと分析データのずれが小さい(モデルのあてはまりがよい)ことを意味します。ただし,逸脱度の大きさは分析に使用するデータによって異なるため,この値がいくつ以下であればよいというような一般的な基準はありません。
AIC, BIC
線形回帰分析における(調整されていない)決定係数が複雑なモデルほど大きくなるのと同様に,逸脱度の値は予測変数の数が多くなればなるほど小さくなる性質を持ちます。そこで,残差逸脱度に対し,モデルに含まれる予測変数の個数(交互作用を含むならその個数も含む)による調整を行った値がAICとBICです。このAICとBICは,線形回帰におけるモデル適合度指標のAIC,BICと同じものです。
AICとBICについても値が小さいほどあてはまりがよいことを示しますが,残差逸脱度と同様に,これらがいくつ以下であればよいという一般的な基準はありません。
モデル全体の検定
ここまで見てきたように,逸脱度やAIC,BICといった指標には,モデルがデータに十分あてはまっているといえるのかどうかの明確な基準がありません。そこで,モデルがデータにあてはまっているかどうかについての検定を行うのが「モデル全体の検定」です。
この「モデル全体の検定」にチェックを入れると,\(\chi^{2}\)(カイ2乗)を用いたモデル適合度の検定を行うことができます(図7.76)。
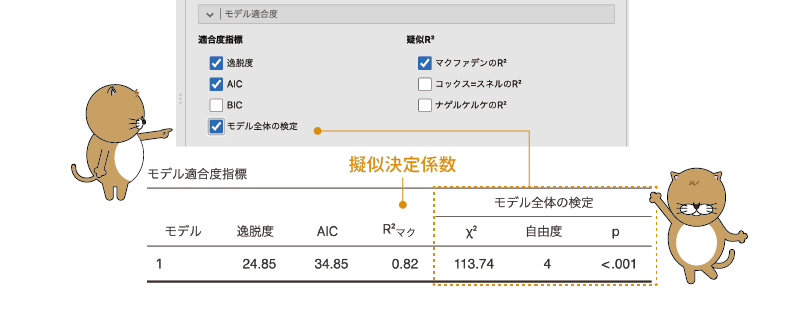
図7.76: 適合度指標とモデル適合度の検定
線形回帰モデルの場合,モデル全体の適合度の検定にはFが用いられますが,2項ロジスティック回帰ではモデルの逸脱度に基づいて算出された\(\chi^{2}\)を用いた検定が行われます。この\(\chi^{2}\)は,切片のみのモデルの残差逸脱度から分析モデルの残差逸脱度を引いた値で,この値が有意である場合(pが有意水準を下回っている場合)は,分析モデルが切片のみのモデルよりもデータをうまく説明できている(残差逸脱度が有意に小さい)ということを意味します。
今回の分析結果ではp<.001で有意ですので,この分析モデルがデータをまったく説明できていないということはなさそうです。ただし,線形回帰モデルのF検定の場合と同様に,この検定が有意であっても,それは説明力0のモデルよりはましであるという意味でしかありませんので,その点には注意が必要です。
擬似R²
逸脱度やAICは,モデルの適合度を相対的に評価するには便利な指標ですが,これらの値だけでは分析モデルがどの程度データをうまく説明できているのかの判断は困難です。そこで,モデルのあてはまりのよさを0から1の範囲の値として示すようにしたものが擬似決定係数です。この擬似決定係数の値は,線形回帰分析における決定係数R²に相当するもので,値が1に近いほどデータをうまく説明できていることを意味します。
マクファデンのR²
jamoviでは,擬似決定係数として,マクファデン,コックス=スネル,ナゲルケルケの3種類の値を算出することができます。この3つのうち,一般にもっともよく知られているのはマクファデンの擬似決定係数で,これは分析モデルの尤度の対数(対数尤度)を切片のみのモデル(帰無モデル)の対数尤度で割り,その値を1から引くことによって求められます。
対数尤度はつねに負の値になり,かつモデルとデータのあてはまりがよいほど0に近い値になるため,このように計算することで,分析モデルのあてはまりがよいほど対数尤度の割り算の部分が0に近い値になり,マクファデンの擬似決定係数は1に近づきます。
7.4.6 モデル係数
ここでは,各予測変数の係数に関する次の項目の設定を行います(図7.77)。
図7.77: 回帰係数の信頼区間
- オムニバス検定 各予測変数についてオムニバス検定を行います。
- 尤度比検定 各予測変数の説明力が0でないかどうかを検定します。
- 推定値(対数オッズ比) 回帰係数の推定に関する設定を行います。
- 信頼区間 回帰係数の信頼区間を算出します。
- オッズ比 各予測変数のオッズ比に関する設定を行います。
- オッズ比 オッズ比を算出します。
- 信頼区間 オッズ比の信頼区間を算出します。
オムニバス検定
各予測変数が従属変数の説明において貢献しているといえるかどうかを確かめたい場合には,「オムニバス検定」の「尤度比検定」にチェックを入れてください。すると,各説明線変数の有効性についての検定結果が表示されます(図7.77)。

図7.78: 予測変数についての尤度比検定
2項ロジスティック回帰の場合には,各予測変数についての検定はANOVA(分散分析)ではなく尤度比検定と呼ばれる手法が用いられます。これは,分析に使用したモデルと,そこからその予測変数を除いたモデルの尤度の比率(尤度比)に基づく検定で,検定統計量には\(\chi^{2}\)が用いられます。そして,その隣のp値が有意水準を下回る場合に,「その予測変数の説明力が0でない」とみなされます。
推定値(対数オッズ比)
線形回帰分析の場合と同様に,2項ロジスティック回帰でも各予測変数の回帰係数について信頼区間を算出することができます。回帰係数の信頼区間を算出するには,「推定値(対数オッズ比)」の「信頼区間」にチェックを入れてください(図7.79)。
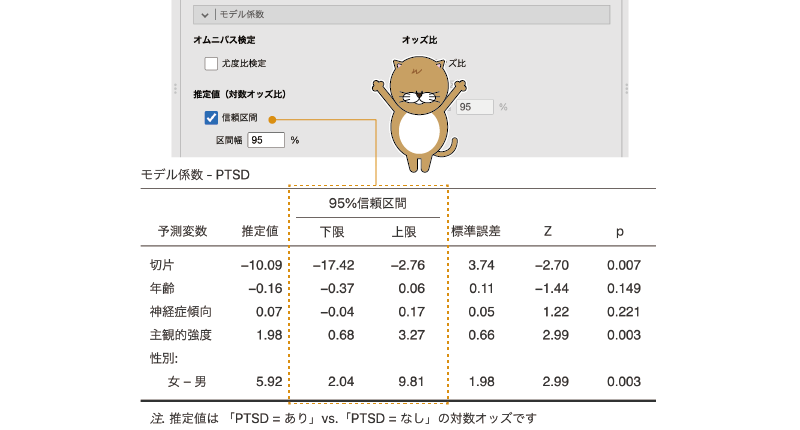
図7.79: 回帰係数の信頼区間
なお,この設定項目の名前には「対数オッズ比」とありますが,これは分析結果のところでも説明したように,2項ロジスティック回帰の回帰係数はロジットの変化量を表しており,そしてそれはオッズ比を対数変換したのと同じ値だからです。
オッズ比
繰り返しになりますが,2項ロジスティック回帰の回帰係数は,予測変数の値が1変化した場合における従属変数のロジットの変化量を表しています。そしてロジットというのはオッズを対数変換したものなので,2項ロジスティック回帰の回帰係数から予測変数の影響の強さを解釈するのは困難です。そこで多くの場合,回帰係数を指数変換してオッズに戻したうえで解釈が行われます。このとき,回帰係数を指数変換した値は,予測変数の値が1増えるとオッズが何倍に変化するかを表す値(オッズ比)になります。
ほとんどの統計ソフトでは,2項ロジスティック回帰の回帰係数をオッズ比に変換してくれる機能があります。そして,それはjamoviでも同じです。jamoviでは,「オッズ比」の1つ目の項目である「オッズ比」にチェックを入れることで,回帰係数をオッズ比に変換した値が表示されます(図7.80)。
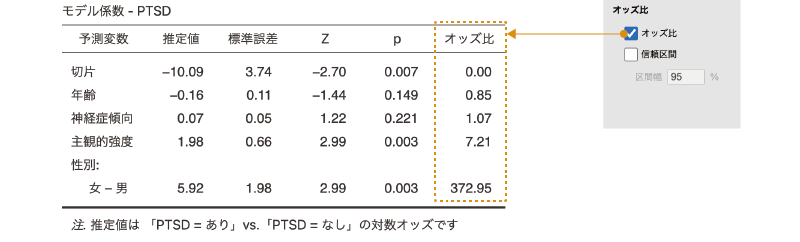
図7.80: オッズ比
また,このオッズ比に対しても信頼区間を算出することができます。オッズ比の信頼区間を算出するには,「オッズ比」の2つ目の項目である「信頼区間」にチェックを入れてください。
7.4.7 予測
2項ロジスティック回帰では,モデルの適合度として逸脱度や擬似決定係数などの値が算出されますが,そうした複雑な数値を使わなくても,もっと単純にモデルの精度を判断する方法があります。それは,このモデルを使って従属変数の値(PTSDあり・なし)を正しく判別できるかどうかを見るという方法です。
2項ロジスティック回帰の場合,従属変数の本来の値は「はい・いいえ」や「あり・なし」のように2種類の値のうちのいずれかしかありません。そのため,モデルよる予測値に基づく判定結果が各対象者の従属変数の値と一致しているかどうかの判断は,線形回帰分析の場合よりもずっと単純だからです。
なお,その際,モデルによる判定結果と実際の従属変数の値の組み合わせのパターンには,表7.2に示した4とおりが考えられます。
| PTSD Y | PTSD N | |
|---|---|---|
| 実際の値 | ||
| PTSD Y | 正解(真陽性) | 誤り(偽陰性) |
| PTSD N | 誤り(偽陽性) | 正解(真陰性) |
このとき,実際のデータにおける「PTSD」の値(「あり」または「なし」)と回帰モデルの判定結果が一致する場合を真陽性,真陰性といい,実際のデータでは「PTSD」の値が「あり」なのに回帰モデルに基づく判定結果が「なし」となってしまうことを偽陰性,その逆に,データでは「PTSD」の値が「なし」なのにモデルの判定結果が「あり」になってしまうことを偽陽性といいます。
また,「PTSD」の実際の値が「あり」であるデータのうち,回帰モデルによって正しく「あり」と判定された割合を感度,PTSDの実際の値が「なし」であるデータのうち,回帰モデルによって正しく「なし」と判定された割合を特異度と呼びます。また,データ全体のうちで正しく判断できた割合,つまり全体に占める真陽性と真陰性の合計の割合のことを精度と呼びます(図7.81)。
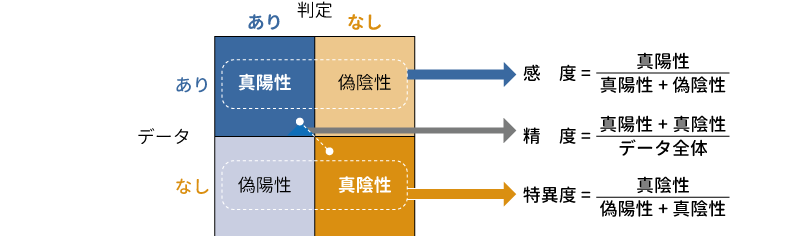
図7.81: 感度,特異度と精度
この感度,特異度,精度はすべてで高いことが望ましいわけですが,実際はなかなかそううまくはいきません。多くの場合,感度を高くしようとすると特異度が下がり,特異度を高くしようとすると感度が下がることになるのです。この関係は,感染症の検査を例に考えてみるとわかりやすいでしょう。絶対に感染者を見逃さないようにしようとして検査の感度を上げる(わずかな兆候でも検査が陽性になるようにする)と,実際には感染していない人に対しても検査結果が陽性になってしまう(偽陽性になる)可能性が高くなります。すると,その検査では「病気に感染していない人」を正しく見分けられないということになり,特異度は低くなります。
この逆に,感染していない人に対して検査が陽性になるのを極力避けようと,よほどはっきりした兆候がない限り結果が陽性にならないようにする(特異度を高くする)と,今度は感染しているのに検査が陽性にならない(偽陰性になる)人が出てきてしまいます。このような性質から,実際の検査では,感染の可能性が少しでもありそうな人を選別するスクリーニング検査(感度を高く設定)と,確実に診断を行うための確定診断検査(特異度を高く設定)を用途に応じて使い分けるといったことが行われているのです。
さて,2項ロジスティック回帰での設定に話を戻しましょう。こうした感度,特異度,精度といった視点からモデルの適合度を評価したい場合には,設定画面のにある設定項目を使用します。ここには,次の項目が含まれています(図7.82)。

図7.82: 予測の設定項目
- カットオフ
- カットオフ・プロット カットオフ値を変化させた場合の感度と特異値の関係を図示します
- カットオフ値 カットオフ値を指定します
- 予測指標(予測指標)
- 分類表 回帰モデルによる分類結果をクロス表に示します
- 精度 モデルの精度を算出します
- 特異度 モデルの特異度を算出します
- 感度 モデルの感度を算出します
- ROC
- ROC曲線 ROC曲線を図示します
- AUC ROC曲線の下の面積(AUC)を算出します
カットオフ
まず,左側にある「カットオフ」の部分では,回帰モデルのカットオフ値と,感度,特異値の関係を見ることができます。ここにある「カットオフ・プロット」にチェックを入れると,その回帰モデルのカットオフ値と感度,特異度が図に示されます。なお,カットオフ値というのは,「あり」・「なし」の判定基準となる境目の値のことです。
このカットオフ値は初期設定では0.5(つまりPTSDが「あり」の確率が0.5(50%)以上であれば「あり」と判定)に設定されています。この分析結果では,カットオフ値が0.5の場合,感度に比べて特異度がやや低いことがわかります。もし特異度を上げたければ,このカットオフ値を0.5より大きな値に設定すればよいわけですが,そうすると感度はカットオフ値が0.5の場合よりもやや下がってしまいます(図7.83)。
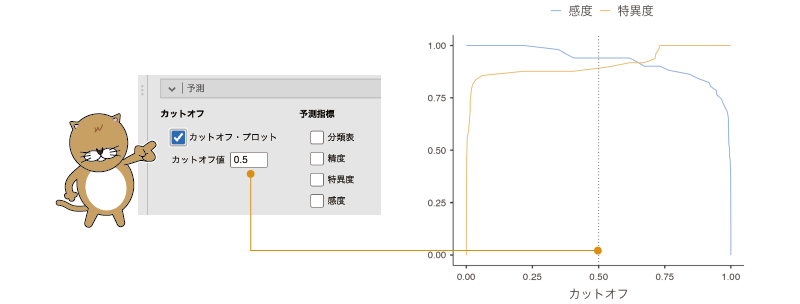
図7.83: カットオフ値と感度・特異度の変化
このカットオフ値をいくつに設定するかは,最終的には感度と特異度のバランスを見ながら分析者が判断することになります。
予測指標
その分析モデルにおける実際の判定結果や感度や特異度について詳しく知りたい場合には,予測指標の項目を使用します(図7.84)。
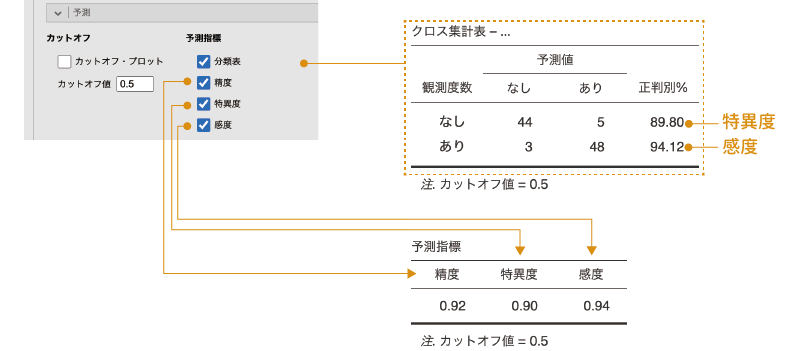
図7.84: 判定結果と予測精度の指標
分類表
1番上の「分類表」にチェックを入れると,分析データに含まれる各対象者がどのように判定されたのかがクロス表の形で表示されます(図7.84)。この表の数値は,設定したカットオフ値を用いて判定した結果です。なお,この表の「観測度数」の「N」の行にある「正判別%」の値は,PTSDの値が「なし」の人が「なし」と判定された割合(つまり特異度),「Y」の行にある「正判別%」の値はPTSD「あり」の人が「あり」と判定された割合(つまり感度)を示しています。
ROC
この設定画面の右側にある「ROC」では,ROC曲線(受信者操作特性曲線)と呼ばれる曲線とその関連指標を用いてモデルの適合度を見ることができます。
ROC曲線
ROC曲線は,回帰モデルのカットオフ値をさまざまに変化させた場合の感度と偽陽性率(\(\mathsf 1 -\)特異度)を図示したものです。設定画面の「ROC曲線」にチェックを入れると,この図が表示されます(図7.85)。
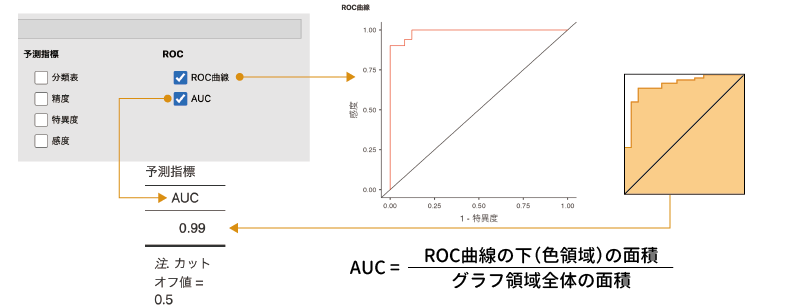
図7.85: ROC曲線とAUC
このグラフが図の中央にある斜め線より上側にある場合には,そのモデルによってPTSDのあり・なしをある程度うまく判定できることを,斜め線と完全に一致する場合には,そのモデルではPTSDのあり・なしをでたらめにしか判定できないことを意味します。
AUC
また,その下にある「AUC」の項目は,このROC曲線の下側の面積(Area Under Curve)がグラフ全体にしめる割合を表したものです。この値は,判定精度の高い回帰モデルほど1に近くなり,まったくでたらめなモデルの場合には0.5になります。このAUC値の解釈については,一般に表7.3のような目安が用いられます。
| AUCの値 | 判定精度 |
|---|---|
| 0.9 〜 1.0 | 高 |
| 0.7 〜 0.9 | 中 |
| 0.5 〜 0.7 | 低 |
サンプルデータの分析結果ではAUCは0.99ですので,作成した回帰モデルはPTSDの有無を高精度で判定できていることがわかります。