9.3 探索的因子分析
ここまで見てきた主成分分析は,複数の変数を総合した得点を作成することによってそこに情報を集約し,変数の数を減らすという手法でした。これに対し,因子分析では,複数の変数の背後にある少数の共通因子を探し出すことによって,データの構造を単純化し,理解しやすくする方法です。
なお,因子分析は大きく探索的因子分析と確認的因子分析と呼ばれるものとに分けられますが,「因子分析」とだけいった場合には,一般に探索的因子分析のことを意味します。そこで,まずはこの探索的因子分析について見ていくことにしましょう。
9.3.1 考え方
ここに,ある高校における学力テスト10教科(国語,英語,日本史,世界史,公民,地理,数学,物理,生物,化学)の成績データがあるとします。このデータを用いて各生徒の学力について分析したいとしましょう。この場合,成績データは10科目分もありますので,なんらかの形でデータの縮約(削減)を行わないと,生徒の学力についての全体像を把握することは困難でしょう。この場合,先ほど説明した主成分分析を用いて,これらの成績を総合した得点を算出するというのも1つの方法ですが,ここでは別の方法を考えてみます。
学校の教科は一般に「文系科目」,「理系科目」などと分類されますが,もしこれらの科目の成績の背後に「文系学力」や「理系学力」のようなものがあり,それらの能力の高さが個別の成績に影響を与えているのだとしたら,そしてそれらの能力の高さをなんらかの形で推定することができるとしたらどうでしょうか。この生徒は文系学力は高いが理系学力がいまいちだ,この生徒は文系学力も理系学力も高い,などのように,よりシンプルな形でそれぞれの学生の学力について検討できるようになるはずです。
たとえば,これら10教科の成績の相関係数が図9.39のようなものになっていたとしましょう。
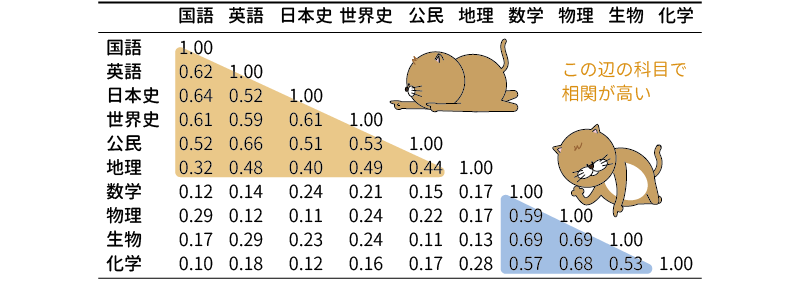
図9.39: 10教科の相関係数の例
この相関行列を見ると,国語から公民まではお互いにだいたい0.4から0.6程度の正の相関があり,数学から化学までの間にも互いに0.5から0.7近い正の相関があります。対照的に,国語や英語と数学や物理の間の相関は0.1や0.2と低いものになっています。これらのことから,国語から公民まで,数学から化学までには成績の点から見た場合にある程度の類似性があり,そして国語や英語などの科目と数学や物理などの科目との間にはそうして類似性が見られないということになります。
因子分析では,このような科目成績間の類似性には,その背後になんらかの共通因子の存在があると考えます。ある共通因子が,程度の差こそあれそれぞれの科目に対して影響を与えているのために,これらの点数が似通ってくると考えるわけです。このようにして考えると,国語から公民までの科目の背後,そして数学から化学までの科目の背後に共通する因子が隠れているといえそうです。
なお,このデータはあくまでも「たとえば」の話として示したもので,かなり誇張した値になっています。ですから,科目間の類似性は相関係数を見ただけでもおおよそわかるのでしょう。しかし,実際のデータではここまでわかりやすい形になっていないことがほとんどです。そこで探索的因子分析では,このような複数の変数の背後にある因子を,数学的な手法を用いて見つけ出そうとするのです。
その際,因子分析では各変数(この例の場合は各教科の成績)と各因子の間の関係を式で表すと次のような形になります。
\[\begin{eqnarray*} \text{国語の成績} &=& a_1 \times \text{因子}_1 + b_1 \times \text{因子}_2 +\text{独自因子}_\text{国語}\\ \text{英語語の成績} &=& a_2 \times \text{因子}_1 + b_2 \times \text{因子}_2 +\text{独自因子}_\text{英語}\\ \text{日本史の成績} &=& a_3 \times \text{因子}_1 +\cdots \end{eqnarray*}\]
主成分分析の場合とよく似ていますが,式の左側は主成分分析の場合のように合成得点ではなく,各教科の成績得点になっています。つまり,共通因子の影響力を合計したものが実際のテスト成績になるという考え方をとるのです。このとき,各因子の前にある\(a_1\)や\(b_1\)はその教科の成績における各因子の影響力の強さを表しており,これは因子負荷量と呼ばれます。このような式は,分析に使用する変数(この例では教科)の個数と同じだけ作成されます。
また,式の最後には「\(\text{独自因子}_\text{国語}\)」というような項目があります。これは,共通因子では説明しきれない,その教科独自の部分を表しており,独自性と呼ばれます。これに対し,その教科の得点のばらつきのうち,共通因子によって説明される部分は共通性と呼ばれます。
このような考え方に基づいて,因子分析では先ほどの関係式でデータをうまく説明できるような因子負荷量を計算していくのですが,先ほどの関係式で分析前に明らかな値は式の左辺にある各教科の成績(これを観測変数と呼びます)のみで,それ以外の共通因子や因子負荷量,独自性(独自因子)の大きさはすべて計算によって求める必要があります。さらに,共通因子がいくつあるのかさえ,分析前にはわからないのです。さすがにこのままではなんでもありな状態になってしまい,最適な値を求めようにも求めようがありません。そこで,因子分析では計算になんらかの条件を設けたうえで,その中で最適と考えられる値を算出するという方法がとられます。
そして,その際にどのような計算上の条件を設けたかによって,因子分析の結果は異なってきます。そのため,因子分析の実施にあたっては,分析をソフトウェア任せにするのではなく,分析者自身が分析データや分析目的に合わせて適切な設定を行うことが非常に重要となります。
9.3.2 基本手順
ここからは,次のサンプルデータ(factor_data03.omv)を用いて探索的因子分析の分析手順についてみていくことにしましょう(図9.40)。
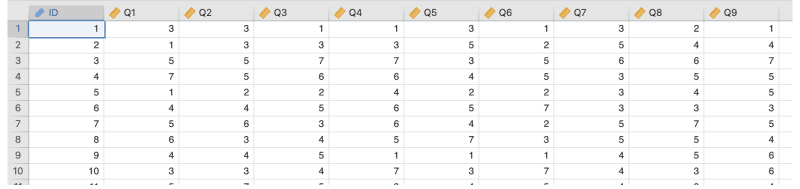
図9.40: サンプルデータ
このデータには,「オタク傾向」の強さを測定ために作成した9個の質問項目に対する回答データ(いずれも「1:まったくあてはまらない」〜「7:とてもよくあてはまる」の7段階評定)が300人分含まれています。これらの質問への回答から,「オタク傾向」の背後にどのような共通因子がありそうかを探ってみます。
ID回答者のIDQ1関心がある対象については徹底して調べ尽くすほうだQ2好きなものを手に入れるためなら手間やお金は惜しまないQ3趣味に関連するアイテムやグッズなどは全部集めたくなるQ4現実の人間よりフィクションのキャラクターのほうがよいと思うことがあるQ5人といるより趣味の時間のほうが楽しいQ6人とは直接話すよりオンラインでやりとりするほうがいいQ7熱くなりすぎて周りに引かれることがあるQ8趣味について話し出すととまらないQ9熱中しすぎて我を忘れることがある
探索的因子分析の実施には,分析タブの「 因子分析」から「探索的因子分析」を選択します(図9.41)。
図9.41: 探索的因子分析の実行
すると,次の設定画面が表示されます。画面の構成は,主成分分析のものと非常によく似ています(図9.42)。
図9.42: 探索的因子分析の設定画面
ここで,分析に使用する観測変数(質問)を右側の「変数」欄に移動したら基本的な分析設定は終了です(図9.43)。
図9.43: 分析する変数を設定
ただし,主成分分析の場合と同様,あるいはそれ以上に,因子分析の結果は分析の設定によって異なります。そのため,分析結果を見る前に,因子分析の各設定項目について説明していきたいと思います。
また,因子分析においても,それぞれの回答者について因子得点を算出することができます。
方法
データの中から共通因子をとり出すことを因子の抽出といいますが,この因子抽出の方法にはさまざまなものがあり,そしてどれを用いるかによって結果が少しずつ変わってきます。また,因子分析の場合,その抽出した因子に対してまず例外なく回転と呼ばれる操作が行われます。そして,その回転の方法によっても,分析結果が大きく変わります。
そこで,ここではこれら因子分析の結果に大きく影響するこれらの設定項目について見ていくことにします。
抽出法
方法の「抽出法」の項目では,因子の抽出方法について設定を行います。今回のサンプルデータの分析では,因子の抽出は初期設定どおり「最小残差法」で行うことにしますが,jamoviで使用可能な因子抽出法には次の3つの選択肢がありますので,ここではそれらについて簡単に説明しておくことにします(図9.44)。

図9.44: 因子抽出法
- 最小残差法 最小2乗法を用いて残差が最小となるように因子を抽出します。
- 最尤法 データの分布に多変量正規分布を仮定し,分析データを説明するモデルとしてもっともあり得そうな(最尤な)因子を抽出します。
- 主因子法 主成分分析と同様の計算を繰り返し行い,計算結果を収束させていくことによって因子を抽出します。
最小残差法
jamoviで用意されている因子抽出法のうち,「最小残差法」は「重みづけなし最小2乗法(Ordinary least squares: OLS)」とも呼ばれる手法で,因子分析モデルとデータの間の残差が最小になるような形で因子の抽出を行います。この方法は,標本サイズが小さめのデータなど,比較的どのようなデータに対しても因子をうまく抽出することができるとされている方法です。
最尤法
2つ目の「最尤法」は,データの分布に多変量正規分布と呼ばれる分布を仮定することによって,その分析データの説明モデルとしてもっともあり得そうな因子を抽出するという方法をとります。近年,多くの研究で用いられるようになった手法であり,数学的にも洗練された方法であるとされますが,計算途中で計算不能になってしまうケースが最小残差法などに比べて多く発生します。また,適切な結果を得るためには十分な標本サイズが必要とされます。
主因子法
3つ目の「主因子法」は,主成分分析と同様に相関係数の固有ベクトルと固有値の計算を行うことによって因子を抽出する方法です。ただし,主成分分析ではこの計算は1度しか行われませんが,主因子法では最初の計算で得られた結果をもとに各変数に対する共通性を算出し,その共通性の値を相関行列の対角(同じ変数同士の相関で値がつねに1.0になる部分)をその共通性の値で置き換えたうえで,再度固有ベクトルと固有値の計算を行う,という手順を複数回繰り返します。最終的に,共通性の値の変化があらかじめ設定した基準値より小さくなった(固有値の値が安定した)ところで計算をストップし,その結果を因子として抽出します。
この主因子法は,最小残差法と同様に,比較的どのようなデータであっても因子を抽出できることが知られています。また,計算が単純であるということから,コンピューターの計算能力がそれほど発達していなかった頃によく用いられてきた方法です。
なお,この主因子法で反復計算を行わず,共通性の初期値を1.0にして(つまり相関行列そのままで)固有値の計算を行って因子を抽出する方法は「主成分法6」と呼ばれ,その結果はjamoviの「主成分分析」を用いた場合の分析結果と同じになります。
回転法
因子分析の目的は,たくさんの変数の背後にある共通因子を見つけ出し,それらがどのような因子であるかを解釈することにあります。しかし,因子分析の結果は,そのままでは解釈困難なことがほとんどです。そこで,この因子の解釈を容易にするために行われるのが因子の「回転」と呼ばれる操作です。
次の例は,10教科の学力テストデータから因子抽出した場合の結果を図示したものだと考えてください。この図では,各教科に対する因子1の因子負荷量を横軸に,因子2の負荷量を縦軸にとって示したものです。因子分析直後の結果では,この図のようにそれぞれの教科が因子1と2の両方から影響(負荷)を受けていて,この因子1や因子2が何を表す因子なのかがよくわかりません(図9.45)。
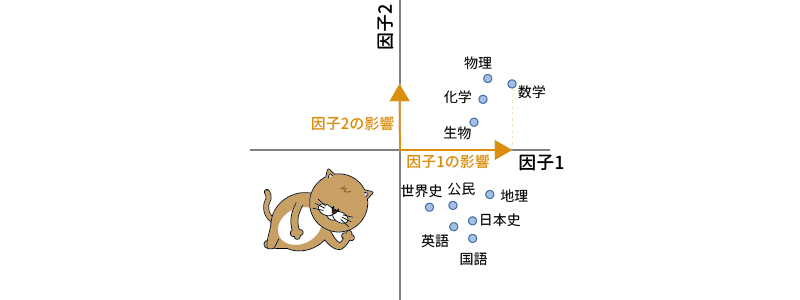
図9.45: 因子抽出直後の状態の例
しかし,たとえば次の図のように,各教科の相対的な位置関係は保ったままでグラフの軸を回転させると,国語や英語などの教科は横軸の近くに,数学や物理などの教科は他の教科は縦軸の近くに集まるようになります(図9.46)。
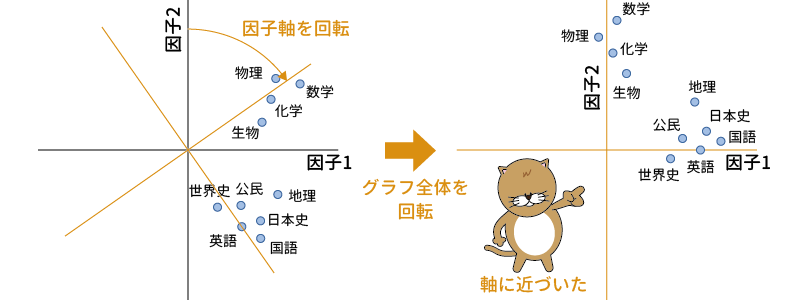
図9.46: 因子の回転
これであれば,横軸(因子1)は国語や英語,日本史などのいわゆる文系科目に強く関連する因子(文系学力因子)であり,縦軸(因子2)は数学や物理,化学などのいわゆる理系科目に強く関連する因子(理系学力因子)である,というように,容易に解釈することができるようになります。このようにして,分析結果を理解可能な形にすることが因子回転の役目です。
その際,因子分析では,分析結果ができるだけ「単純構造」に近くなるようにして因子の回転を行います。単純構造とは,それぞれの変数が複数の共通因子のうちのいずれか1つからのみ影響を強く受けている状態,つまり,先ほどの図でそれぞれの変数がいずれかの軸にできるだけ近くなるような状態のことです。
また,因子の軸を回転させる際,それぞれの軸が直角に交わった状態を維持したままで回転させる方法はとくに直交回転と呼ばれます。この直交回転では,それぞれの因子の間の相関は0になります。これに対し,因子の軸が互いに直角であるという条件をおかずに回転させる方法は斜交回転と呼ばれます。一般的には,直交回転よりも斜交回転のほうが,単純構造に近い結果が得られやすくなります。
なお,かつては直交回転が一般的でしたが,それは当時のコンピューターの計算能力では計算が複雑になりがちな斜交回転は難しかっかたらというのが大きな理由の1つでした。現在のコンピューターではそのようなことはありませんので,近年は因子が互いに独立であるという強い仮説でもない限り,斜交回転を用いることが一般的になりつつあります。
因子の回転方法にはじつにさまざまなものがありますが,jamoviではそのうち次の6つが利用できるようになっています。今回のサンプルデータの分析では,因子の回転法についても初期設定どおり「オブリミン法」で行うことにしますが,次に各回転方法について簡単に説明を加えておきます(図9.47)。
図9.47: 因子の回転方法
- なし
- バリマックス
- クォーティマックス
- プロマックス
- オブリミン
- シンプリマックス
なし
これは因子回転を行わないという設定です。何らかの理由で途中の計算結果を参照したい場合などを除いて,因子分析において回転を「なし」にすることはおそらくほとんどないでしょう。
バリマックス
バリマックス(Varimax)法は直交回転におけるもっとも一般的な手法です。この回転方法では,因子ごとに因子負荷量(の2乗)の分散が最大になるように,つまり,ある因子について,特定の変数に対しては負荷量の絶対値が大きく,他の因子に対しては小さくなるようにして因子軸を回転させます。
クォーティマックス
クォーティマックス(Quatimax)法も直交回転における手法の1つです。この方法では,それぞれの変数に対する各因子の負荷量にメリハリがつくようにして因子の軸を回転させます。この方法は,どの変数に対しても1つ目の因子の負荷量が高くなりがちで,すべての変数に対して影響を与える全般因子的なものが抽出されやすいことが知られています。
プロマックス
プロマックス(Promax)法は斜交回転における代表的な手法の1つです。この回転方法では,まずバリマックス回転によって得られた因子負荷を4乗7して因子負荷量のメリハリを強調した状態を作成し,最終的な結果をそれに近づけるようにして因子の回転を行います。
「斜交回転といえばプロマックス法」といえるほどによく使用される回転方法ですが,この方法はあくまでも簡便法であり,適切な結果を得るには別の回転法が望ましいとする考えもあります。
オブリミン
オブリミン(Oblimin)法は斜交回転における手法の1つです。この方法では,各因子間で因子負荷(の2乗)の共分散が最小になるような形で因子の回転を行います。なお,オブリミン法はいくつかの斜交回転法をひとまとめにした総称で,jamoviの「オブリミン法」の結果は,そのうちのクォーティミン法(Quartimin)による回転結果と一致します。
シンプリマックス
シンプリマックス(Simplimax)法も斜交回転における手法の1つです。この方法では,因子負荷行列(各変数に対する因子負荷量をまとめた表)において「因子負荷が0」である箇所が特定の個数になるように回転させます。「因子負荷が0」である箇所の個数を指定して分析できる統計ソフトもありますが,jamoviで「シンプリマックス」による回転を行った場合,「因子負荷量が0」の箇所が分析に使用した変数と同じ個数になるような形で回転が行われます。
因子数
主成分分析の場合と同様に,因子分析においても計算上は分析に使用する変数と同じ個数だけ因子を抽出することができます。実際の分析では,その中からとくに重要な因子だけをとり出して解釈することになります。因子の個数の決め方はすでに主成分分析のところで説明したのとまったく同じですので,ここでは説明は省略します。
なお,サンプルデータの分析では,因子の個数は平行分析によって決める(平行分析に基づく)ことにします。その結果,3つの因子が抽出されたはずです。
前提チェック
因子分析の前提についても,設定に含まれている項目やその使用方法,解釈の方法は主成分分析のところで説明したのと同一です。詳細は主成分分析における前提チェックの項目を参照してください。
因子負荷量
因子負荷量の項目についても,設定項目やその使用方法は主成分分析のところで説明したのと同じです。ここでは,結果の解釈をしやすくするために「負荷量順に並び替え」にチェックを入れておくことにします。
追加の出力
「追加の出力」には,次の項目が含まれています(図9.48)。

図9.48: 追加の出力
- 因子の要約量
- 因子の相関
- モデル適合度指標
- 回転前の固有値
- スクリープロット
因子の要約量
最初の「因子の要約量」の項目にチェックを入れると,因子に関する要約情報として図9.49のような結果が表示されます。

図9.49: 因子の要約量
このうち,「負荷量2乗和」は各因子の因子負荷量の2乗値の合計で,これはその因子で説明できる情報の量を表します。その隣の「分散説明率(%)」は,データ全体の分散のうち,その因子によって説明される情報量の割合(因子寄与率),一番右端の「累積%(累積寄与率)」はその因子までの寄与率の合計です。
この表は,因子抽出法を「最小残差法」,因子の回転法を「オブリミン法」にして分析した結果についての因子の要約ですが,この結果からは,3つの因子がそれぞれ比較的均等な割合でデータを説明できていることがわかります。また,3つの因子による累積寄与率は57.65%で,これら3つの因子でデータ全体の6割近くを説明できていることから十分といえるでしょう。
因子の相関
「因子の相関」にチェックを入れると,各因子間の相関係数が図9.50のように相関行列の形で表示されます。

図9.50: 因子の相関
この相関行列から,3つの因子の間には互いに中程度からやや弱めの正の相関があることがわかります。
モデル適合度指標
「モデル適合度指標」の項目にチェックを入れると,図9.51のような表が追加で作成されます。

図9.51: モデル適合度指標
この表には,左から順にRMSEA,RMSEAの90%信頼区間,TLI,BIC,モデルに対する\(\chi^2\)適合度検定の結果が表示されています。
一番左のRMSEA(近似誤差2乗平均平方根)は,回帰分析のところで出てきたRMSE(誤差2乗平均平方根,第7章のモデル適合度を参照)の近似値で,この値が小さいほど,分析によって得られた因子モデルとデータのずれ(残差)が小さいことを意味します。一般には,このRMSEAの値が0.05未満の場合にモデルの適合度が良好であるとみなされます。また,RMSEAについては90%(95%ではない点に注意)の信頼区間と合わせて報告されるのが一般的です。
その隣のTLIはタッカー=ルイス指数と呼ばれる値で,これは独立モデル(因子と各変数の間の関係をまったく考えないモデル)に対して分析モデルのあてはまりがどれだけ改善されているかを示します。一般には,この値が0.95以上である場合にあてはまりがよいとみなされます。
TLIの隣のBIC(ベイズ情報量規準)は,回帰分析のモデル適合度のところで説明した値と同じものです。この値はモデルのあてはまりのよさを相対的に示す数値で,この値1つだけでは,モデルが十分に適合しているかどうかの判断はできません。
表の一番右端の「モデルの検定」の部分には,モデルとデータのずれの大きさについての\(\chi^2\)適合度検定の結果が示されています。この検定は「モデルとデータのずれは0である」という帰無仮説に対するものなので,この検定結果が「有意でない」ことが望ましいといえます。ただし,この\(\chi^2\)の値は標本サイズが大きいほど,また分析に使用する変数の個数が多いほど有意になりやすい傾向にあるため,この検定結果が有意だったからといって,必ずしもモデルがデータに適合していないというわけではありません。
今回のサンプルデータの分析結果では,RMSEAは0.01と非常に小さく,TLIは1.00,\(\chi^2\)検定の結果も有意ではありませんので,モデルの適合度は十分なと考えてよいでしょう。
回転前の固有値
この設定項目にチェックを入れると,因子回転前の固有値に関する情報が表示されます。この設定項目で表示される内容は主成分分析の場合と同じですので,説明は省略します。
スクリープロット
スクリープロットについても主成分分析の場合と同じですので説明は省略します。
9.3.3 保存
因子分析でも,各対象者について各因子の因子得点を算出し,それを別の分析に使用することが可能です。設定画面の一番下にあるを展開すると「因子得点」の設定項目がありますので,ここにチェックを入れると因子得点が新たな変数として作成されます(図9.52)。

図9.52: 因子得点の推定法
ただし,主成分得点と違って因子得点は答えが1つに決まらないため,これをどのように算出するかについては複数とおりの考え方があり,それぞれの方法で算出される因子得点の性質が少しずつ異なります。jamoviに用意されている因子得点の算出方法は,次の5つです。
- サーストン サーストン(Thurstone)法による因子得点の算出を行います。
- バートレット バートレット(Bartlett)法による因子得点の算出を行います。
- テン・ベルヘ テン・ベルヘ(ten Berge)法による因子得点の算出を行います。
- アンダーソン=ルビン アンダーソン=ルビン(Anderson-Rubin)法による因子得点の算出を行います。
- ハーマン ハーマン(Harman)法による因子得点の算出を行います。
なお,ここで作成される因子得点は,いわゆる「洗練された(refined)」因子得点です。因子得点として因子の負荷が大きい項目の合計点や平均点を用いる方法もよく用いられますが8,それらの得点は新たな「計算変数」として作成するか,信頼性分析の機能を用いて合成変数を作成するなどの方法を用いてください。
サーストン
サーストン法は回帰法とも呼ばれる方法で,回帰モデルを用いて因子の得点を推定しようとする方法です。より具体的には,変数間の相関行列の逆行列と因子負荷行列を使って因子得点算出のための係数を作成し,この係数を(標準化済みの)各測定値に掛けて因子得点を算出します。
なお,探索的因子分析で抽出される因子は平均値が0,分散が1になるように標準化されていますが,この因子得点の平均は0,分散は回帰モデルの重相関係数の2乗に等しくなり,1にはなりません。また,この方法は,対応する因子と因子得点の間の相関が最大になるように因子得点を算出しますが,他の因子との関係については正確さがやや欠けるため,直交回転された因子についての因子得点であっても,因子得点間の相関が0にならない場合があります。
サーストン法(回帰法)は因子得点算出の方法としてはおそらくもっとも一般的な手法で,他の多くの統計ソフトでも採用されています。
バートレット
バートレット法は,サーストン法に改良を加えたもので,共通因子による影響のみを考慮して因子得点を算出します。この方法で算出された因子得点は,「真の」因子得点の不偏推定値9になりますが,直交因子の因子得点間の相関が完全に0になるわけではありません。また,この方法による因子得点も,因子ごとの平均値は0になりますが,分散は1にはなりません。
テン・ベルヘ
テン・ベルヘ法は,斜交回転された因子の相関をできるだけ正確に反映させるような形で算出される因子得点で,アンダーソン=ルビンの因子得点を斜交回転に拡張したような性質を持ちます。アンダーソン=ルビンの因子得点と同様に,この因子得点の平均値は0,分散は1になりますが,バートレット法の因子得点のような不偏推定値にはなっていません。
アンダーソン=ルビン
アンダーソン=ルビン法は,直交する因子の因子得点間の相関が0になるようにして算出される因子得点です。また,この因子得点の平均値は0,分散は1になりますが,バートレット法の因子得点のような不偏推定値にはなっていません。
ハーマン
ハーマン法は,測定値そのものではなく,因子分析結果から再構築された「理想化された」測定値を用いて因子得点を算出します。この方法は回帰法の修正版で,因子得点の平均値は0になりますが,分散は1にはなりません。
9.3.4 分析結果
サンプルデータについて,「最小残差法」で3因子(因子数は平行分析で決定)を抽出し,「オブリミン法」で回転した結果は図9.53のとおりです。なお,結果の表示については因子負荷の設定項目で「負荷量順に並び替え」にチェックを入れて変数の表示順序を因子負荷量の大きさ順に並び替えてあります。
また,因子間の相関係数についても,追加の出力で「因子の相関」にチェックを入れて算出してあります。

図9.53: 探索的因子分析の結果
この結果の表には,それぞれの質問項目に対する各因子の負荷量と,各質問項目の独自性の値が示されています。このようにして各変数に対する因子負荷をまとめたものは因子パターン行列と呼ばれます。因子の回転を行わない場合や直交回転を用いた場合には,これらの値は因子と各変数の間の相関係数と同じになりますが,斜交回転の場合にはそうではありませんので,その点には注意が必要です。
では,分析結果を見てみましょう。まず,どの質問項目においても独自性が極端に高いことはありませんので,これらの質問への回答は抽出した共通因子で説明できていると考えてよさそうです。もし,分析の結果において独自性が0.8を上回るような質問項目(観測変数)があった場合には,それらは分析から除外したほうがよいでしょう。
また,この表では因子負荷量の絶対値が0.3未満のものは非表示になっています。このようにしてみると,Q7からQ9は因子1のみから強い負荷を,Q4からQ6は因子2のみから強い負荷を受けているというように,この分析結果が単純構造に近いものになっていることがよくわかります。
今回の分析ではそのような質問項目(観測変数)はありませんでしたが,もし,単純構造を乱すような観測変数,つまり複数の因子の負荷が高い変数が含まれている場合には,それらを分析から除外して再分析することもありますし,分析の目的によっては,そのような変数をそのままにしておく場合もあります。ただし,そのように複数の因子にまたがる変数が多数あるような場合には,分析結果の解釈には注意が必要です。
なお,分析結果を解釈する際には,このように絶対値の小さい負荷量は非表示にしたほうが単純構造になっているかどうかの確認がしやすいのですが,論文やレポートに結果を報告する際には,設定画面の因子負荷の「これ未満の負荷量を隠す」に0を入力し,すべての負荷量を表示されるようにしたほうがよいでしょう。
因子の解釈
因子分析では,分析によって抽出された因子をどのように解釈できるかということも,分析における重要な関心の1つです。因子の解釈とは,それぞれの共通因子が一体何を意味するものなのかがわかるように,因子にわかりやすく簡潔な名前をつけることをいいます。
たとえば,この分析結果では,因子1は「Q8」,「Q9」,「Q7」の3つの質問に高い負荷を持っていますが,これらの質問は次のとおりの内容でした。
- Q7 熱くなりすぎて周りに引かれることがある
- Q8 趣味について話し出すととまらない
- Q9 熱中しすぎて我を忘れることがある
これらの質問内容を見ると,いずれも「熱くなる」部分で共通しているようです。ですので,この因子を「熱中傾向」と名づけることにしましょう。
このように,各因子が高い負荷をもつ観測変数にどのような共通点があるのかを見ながら,因子に名前をつけていくのが因子の解釈です。
同様にして因子2,因子3についても解釈してみましょう。因子2は「Q4」から「Q6」に高い負荷を持っています。
- Q4 現実の人間よりフィクションのキャラクターのほうがよいと思うことがある
- Q5 人といるより趣味の時間のほうが楽しい
- Q6 人とは直接話すよりオンラインでやりとりするほうがいい
これらの質問内容は,いずれも人と接することを好まない傾向を示していますので,「非社交性」などと解釈するのが適当でしょう。
また,因子3は「Q1」から「Q3」に高い負荷を持っています。
- Q1 関心がある対象については徹底して調べ尽くすほうだ
- Q2 好きなものを手に入れるためなら手間やお金は惜しまない
- Q3 趣味に関連するアイテムやグッズなどは全部集めたくなる
これらの質問内容は,いずれもモノや情報を徹底して集めたいという部分で共通点が見られますので,ここではこれを「収集欲求」と名づけることにしましょう。
このようにして因子を解釈すると,「オタク傾向」には大きく「熱中傾向」,「非社交性」,「収集欲求」が関連しているということがわかります。また,これらの3因子の間には3.35から0.48の中程度の正の相関がありますので,熱中傾向が強い人ほど非社交的で収集欲求も強い傾向にあるということがわかります。このように,因子分析によってたくさんの変数を共通因子に還元することによって,データ全体を非常に簡潔に説明できるようになるのです。