8.1 2値目的変数[2項検定]
とりうる値が「はい・いいえ」のように2種類しか存在しない2値変数について,その値の「はい・いいえ」の比率が基準の比率,または想定される比率と同じかどうかを確かめたい場合には,2項検定と呼ばれる検定方法が用いられます。
jamoviでは,従来型の一般的な方法による2項検定の他に,ベイズ統計の考え方を用いた検定を実施することも可能です。
8.1.1 考え方
次の例について考えてみましょう。同月齢の80人の幼児を対象としてある認知課題を実施しました。この課題は,この月齢の幼児では通過率70%といわれてきたのですが,今回の実施で課題を通過したのは80人中46人(通過率57.5%)でした(表8.1)。この課題の通過率は,本当に70%なのでしょうか。
| 人数 | % | |
|---|---|---|
| 結果 | ||
| 通過 | 46 | 57.5% |
| 非通過 | 34 | 42.5% |
| 計 | 80 | 100% |
この例のように,測定値のとりうる値が「通過」または「非通過」の2とおりしかない場合,そのデータにおける「通過」または「非通過」の比率がどのように分布するかは,2項分布と呼ばれる確率分布を用いて確率的に求めることができます。
たとえば,この課題の通過率が実際に70%だったとしたとき,無作為に選んだ80人を対象とした調査で80人のうちの70%,つまり56人が課題に通過する確率は,2項分布を用いて計算すると0.0969…で,約9.7%の確率です1。これは一見すると低いようにも感じられますが,全体(母集団)における比率が70%だからといって,そこから抽出した標本で毎回70%ちょうどになるわけではありません。それより1人少ない55人の場合や1人多い57人の場合を含めて考えてみると,80人中55人が通過する確率は0.093(9.3%),80人中57人なら0.095(9.5%)ですので,課題の通過者が80人中55〜57人になる場合であれば28%程度の確率で生じうるわけです。
先ほどは説明のために70%ちょうどの56人から前後1人の幅で考えましたが,実際の場面ではこれよりもっとばらつくことは普通にあるでしょう。極端な話,80人全員が課題に通過する場合や,その逆に全員が通過できない場合というのも,非常にまれなことには違いないですが,確率的には0ではありません。
そこで,母集団における通過率が70%である場合に,80人の標本で通過者が0人である場合から80人である場合までのすべての場合について確率を算出し,それを図示したのが図8.2です。
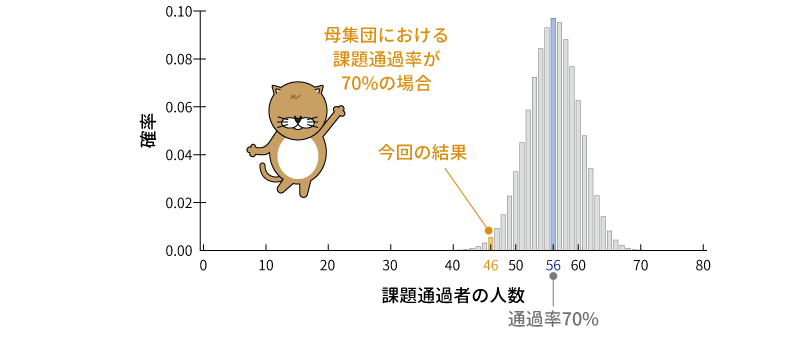
図8.2: 母集団における通過率が70%の場合の確率の分布
さすがに通過者が0人の場合や80人の場合というのは確率的には数値が小さすぎてグラフ上では0になってしまいますが,こうしてみると,母集団における通過率が70%の場合に,今回の結果のように通過者が46人になるというケースはそれなりにありうることだというのがわかります。とはいえ,今回の結果と同じか,あるいはそれよりも極端な結果になる確率というのはかなり小さく,確率的に見てまれな出来事であることには違いありません。
このように,2項検定では想定される比率をもつ母集団から標本データで得られた比率(およびそれより極端な比率)が得られる確率がどの程度であるかを算出します。そして,その確率が有意水準よりも小さい場合に,想定される母集団における比率と標本データの母集団の比率が有意に異なると判断します。
8.1.2 分析手順
分析に入る前に,先ほどの調査結果を次のようにスプレッドシートに入力しましょう(図8.3)。なお,人数は実際には連続変数ですが,分析の都合上,ここでは「名義型()」として設定してください。

図8.3: サンプルデータ
結果課題の結果(通過,非通過)人数通過・非通過の人数(通過:46人,非通過:34人)
それでは分析です。2項検定は,分析タブの「 度数分析」で「1標本比率検定」のところにある「2値目的変数[2項検定]」を選択して実行します(図8.4)。
図8.4: 2項検定の実行
すると,図8.5のような画面が表示されます。
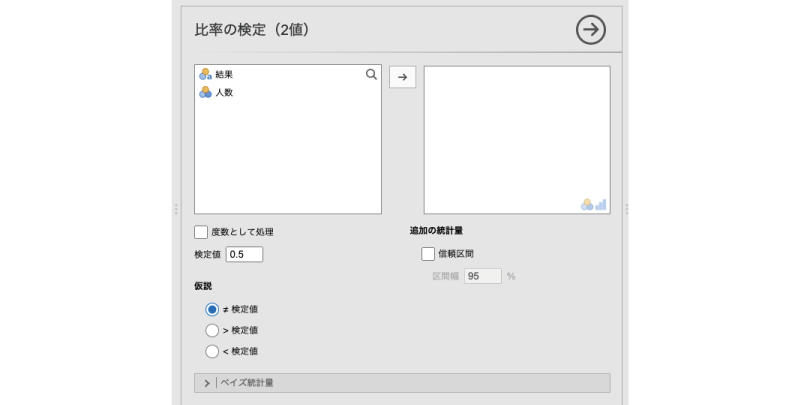
図8.5: 2項検定の設定画面
- 度数として処理 度数が入力されている変数で分析を行う場合に使用します。
- 検定値 比較対象に使用する比率を指定します。
- 仮説 検定の対立仮説に関する設定を行います。
- ≠ 検定値 比率が検定値と異なるかどうかを検定します(両側検定)
- > 検定値 比率が検定値より大きいかどうかを検定します(片側検定)
- < 検定値 比率が検定値より小さいかどうかを検定します(片側検定)
- 追加の統計量 追加の統計量に関する設定を行います。
- 信頼区間 比率の信頼区間を算出します。
- ベイズ統計の手法を用いて検定する場合の設定項目です。
ここで,図8.6のように設定を行います。まず,「人数」を選択して右側に移動してください。下のアイコンを見てもらえばわかるように,この欄には,名義型()か順序型(
)の変数でなければ移動することができません。先ほど「人数」を名義型に設定したのはこのためです。
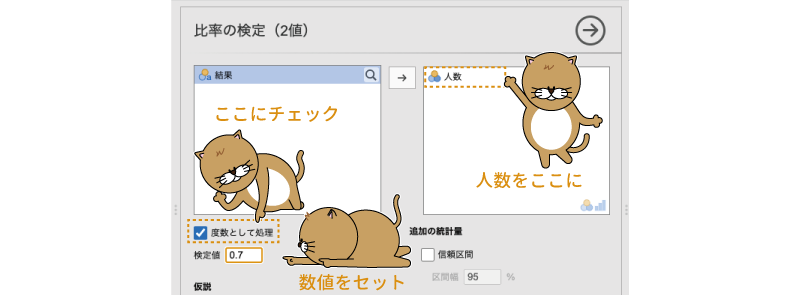
図8.6: 2項検定の分析設定
また,今回の分析データでは,課題通過者,非通過者の人数(度数)をデータとして入力してありますので,「度数として処理」にチェックを入れます。各対象者の「通過・非通過」の結果が1行ずつ入力されている場合には,このチェックは必要ありません。
それから,今回の仮説では,「この課題の通過率は70%(0.7)である」というのが正しいといえるかどうかを確かめたいので,「検定値」の値は「0.7」に設定します。
基本の設定はこれで終了ですが,それ以外の設定項目についてもここで見ておきましょう。
仮説
「仮説」では,検定に使用する対立仮説の設定を行います。
- ≠ 検定値 比率が検定値と異なるかどうかを検定します(両側検定)
- > 検定値 比率が検定値より大きいかどうかを検定します(片側検定)
- < 検定値 比率が検定値より小さいかどうかを検定します(片側検定)
今回のデータでは,想定される母集団の比率どおりであれば80 × 0.7 = 56,課題通過者は46人なので,仮説は「< 検定値」にすべきではないかと思う人もいるかもしれません。ですが,統計的仮説検定の仮説はデータを見る前に設定するものなので,その場合,観測データで通過率が0.7より高いか低いかは見当がつきません。そこで,ここでの検定における対立仮説は「≠ 検定値」で両側検定とします。
8.1.3 分析結果
それでは結果を見てみましょう。分析結果は,図8.7のような形で示されます。

図8.7: 2項検定の分析結果
課題通過者の人数,非通過者の人数という集計結果をデータとして分析を行った場合,結果にはどちらが「通過」でどちらが「非通過」なのかは示されませんので,結果を見る際には注意してください。結果には,スプレッドシートに入力した順に「水準」欄に「1」,「2」として表示されます。分析に使用したデータでは1行目に通過者の人数,2行目に非通過者の人数を入力しましたので,この結果では水準が「1」の方が通過者です。
分析結果には,通過者の比率と非通過者の比率のそれぞれについての分析結果が示されますが,ここで見る必要があるのは通過者の比率(水準が1の行)の結果のみです。
この分析結果ではp = 0.020ですので,80人中46人が通過(通過率57.5%)という比率は,想定される通過率70%とは有意に異なるということがいえます。
8.1.4 ベイズ統計量
すでに分析結果は得られましたが,jamoviの2項検定ではベイズ統計の考え方を用いた検定も可能ですので,その方法についても見ておくことにしましょう。
まず,先ほどの分析結果をクリックして,2項検定の分析設定画面を開いてください。設定画面のを展開すると,次の設定項目が表示されます(図8.8)。
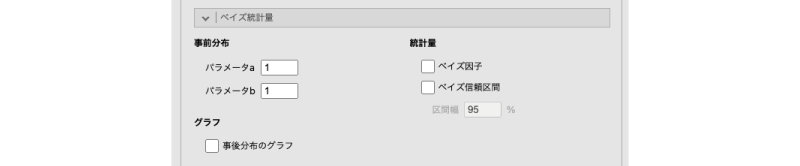
図8.8: ベイズ統計量の設定画面
- 事前分布
- パラメータa ベータ分布のaを設定します。
- パラメータb ベータ分布のbを設定します。
- グラフ
- 事後分布のグラフ 事後分布を図示します。
- 統計量
- ベイズ因子 ベイズ因子を算出します。
- ベイズ信頼区間 ベイズ信頼区間(確信区間)を算出します。
事前分布
ベイズ統計の詳細についてはベイズ統計の教科書を参照して欲しいと思いますが,ベイズ統計では,分析対象についての確率分布をあらかじめ設定し,その分布に対して観測データを与えて分析結果を得るという手順で分析を実施します。この際,分析対象についてあらかじめ設定する分布のことを事前分布と呼びます。の「事前分布」の部分は,この事前分布についての設定です。
jamoviの2項検定では,分析の事前分布としてベータ分布と呼ばれる確率分布を使用することができます。このベータ分布は,aとb(またはαとβ)という2つのパラメータ2をもち,この2つの値の設定の仕方によって,じつにさまざまな形状の分布を表現することが可能です。そして,このベータ分布のパラメータaの値を「パラメータa」の入力欄に,パラメータbの値を「パラメータb」の入力欄に入力します。
しかし,パラメータの値を2つ入力してください,といわれても,どんな値を入力したらよいのか検討もつきませんね。すでに先行研究や予備調査などで分析対象のおおよその分布がわかっている場合には,事前分布がその形状になるようにaとbを設定することになりますが,そうでない場合,一般には特別な情報をもたない分布を事前分布として使用するという方法が用いられます。そしてその場合,もっとも一般に用いられる分布が一様分布と呼ばれる分布です。
この一様分布は,「サイコロの1から6の目が出る確率はすべて1/6で等しい」というように,どのような結果になる確率もすべて同率で等しいとする分布です。ベータ分布では,「a = b = 1」の場合にこの一様分布が得られます。jamoviの分析画面では,「パラメータa」も「パラメータb」も初期設定値は「1」になっていますが,それはこのような理由からです。ここでは「実際の課題通過率」に関して特別な仮説は持ち合わせていませんので,初期設定値どおり,aもbも「1」のままにしておきましょう。
統計量
次に設定するのは「統計量」の部分です。ここの「ベイズ因子」の部分にチェックを入れない限り,ベイズ統計による分析結果は表示されません。ですので,ベイズ統計量が必要な場合には,「ベイズ因子」にチェックを入れておきましょう。
その下の「ベイズ信頼区間」は,ベイズ信頼区間あるいは確信区間などと呼ばれる,ベイズ統計の考え方にそった区間推定値を算出するための設定です。名前はよく似ていますが,従来型の推測統計における「信頼区間」とは別物ですので注意してください。ここでは,この設定はオフのままにしておきます。
ここまでの設定が終わったところで分析結果を見てみると,先ほどの結果の表の右端に,「ベイズ因子\(_{10}\)」という欄が追加されているはずです(図8.9)。

図8.9: ベイズ因子の計算結果
ベイズ統計の場合も,分析結果の表で見る必要があるのは課題通過者についての行(水準が1の行)だけです。この行のベイズ因子の値は2.24で,これは対立仮説が正しい場合の確率が,帰無仮説が正しい場合の確率に比べて2.24倍大きいということを意味しています。
このベイズ因子の大きさの解釈については,複数の研究者によってさまざまな目安が提供されていますが,そのうちの1つ,Kass & Raftery (1995)3では,表8.2のように示されています。一般には,この値(ベイズ因子\(_{10}\))が3を超える場合に,対立仮説を支持する証拠があるとみなされることが多いようです。
| ベイズ因子 | 根拠としての強さ |
|---|---|
| 150〜 | 非常に強い |
| 20〜150 | 強い |
| 3〜20 | 肯定的 |
| 1〜3 | 取るに足りない |
今回の分析結果ではベイズ因子は2.24でしたので,対立仮説を支持する証拠としては弱いものです。つまり,この分析結果からは,「課題の通過率は70%ではない」とはまではいえないことになります。
グラフ
最後に,「グラフ」の設定についても見ておきましょう。この「事後分布のグラフ」にチェックを入れると,課題通過と非通過のそれぞれについて,事前分布,尤度,事後分布を示したグラフが表示されます(図8.10)。ここでは,課題通過の場合についてのプロットを見てみましょう。
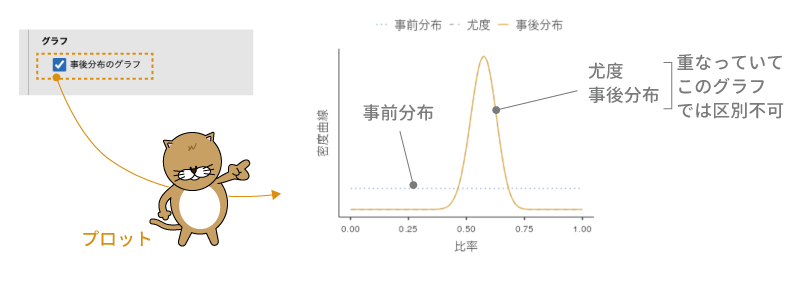
図8.10: 課題通過率についての事前・事後分布のグラフ
このグラフの横軸には通過率,縦軸には確率密度が示されています。確率密度というのは確率とはまた別物なのですが,ここでは大まかに確率の高さを表していると考えてもらって構いません。少し見づらいですが,グラフ中の青の点線が事前分布(一様分布)で,黄色の曲線が事後分布です。
このグラフを見ると,0.575周辺での確率がもっとも高く,そこから離れるにつれて確率が低くなっていくのがわかります。これは,80人中46人が課題通過というデータが得られた場合に,その母集団における通過率(母比率)は0.575周辺である可能性がもっとも高く,それより離れた値である可能性は低いということを示しています。
この事後分布のグラフでは,母集団における通過率が0.7である可能性というのは実際にはかなり低いことがわかります。ただし,先ほど分析結果でみたベイズ因子の値が示す限りでは,この程度であっても「この標本の母集団における通過率は70%ではない」というには証拠としてまだ弱いのです。
2項分布の計算式やその具体的な計算方法については本書では省略します。統計法の教科書などを参照してください。↩︎
分布の形状を決める値のことです。2項分布では試行数nと確率pが,正規分布では平均値と分散(または標準偏差)がパラメータとなります。↩︎
Kass, R. E. & Raftery, A. E. (1995). Bayes Factors. Journal of the American Statistical Association, 90, 773–795. doi:10.1080/01621459.1995.10476572↩︎