7.3 線形回帰

相関係数というのは，ペアになる2つの変数のうち，一方の値が大きくなればもう一方の値も大きくなるといった，変数間の関係についての指標です。変数間にこうした関係が見られるのであれば，一方の値からもう一方の値の大きさについて，ある程度の推測ができるはずです。このような考え方に基づいて，関心のある変数を他の変数からどの程度推測（説明）できるかを見るのが回帰分析です。

7.3.1 考え方

まず，回帰分析の基本的な考え方を見ておきましょう。

次の例について考えてみてください。

Ａさんは，健康上の理由からダイエットを始めました。ダイエットのためにＡさんがしていることは運動（ウォーキング）です。ダイエット開始前のＡさんの体重は80kgでした。

この場合，運動量と体重の間には「運動量が増えるほど体重が減る」という関係があることでしょう。これは負の相関です。このような関係がある場合，次のようにして1日あたりの運動量からAさんの1か月後の体重を大まかに予想することが可能になります。

まず，ウォーキングによる消費カロリーは1時間で「250kcal」程度になるそうです。ここで，今後1か月間に毎日1時間のウォーキングを行ったとしましょう。その場合，1か月間のウォーキングによる「250 × 30 = 7500kcal」を追加で消費することになります。また，人間の脂肪「1kg」のエネルギー量はだいたい「7200kcal」に相当するのだそうで，ということは，毎日1時間のウォーキングを1か月間続けた場合の消費カロリーは，「7500 ÷ 7200 = 1.04…」でおおよそ脂肪1.04kg分ということになります。

もちろん，実際には食事量などの影響もありますのでここまで単純ではありませんが，上記のような関係があるのであれば，毎日1時間のウォーキングを1か月続けると1か月後には体重が1.04kg減，毎日2時間のウォーキングなら体重が2.08kg減になると予測できます。

このことをごく単純な関係式の形で表すと，次のような形になります。

\[\begin{align*} \text{1か月後の体重} & = \text{現在の体重} - \text{運動で消費される脂肪の量} \\ & = 80\text{kg} - 1.04 \times \text{毎日のウォーキング時間} \end{align*}\]

この式が「毎日のウォーキング時間」から「1か月後の体重」を予測（説明）する形になっているのがわかるでしょうか。つまり，「現在の体重」に加えて「毎日のウォーキング時間」さえわかれば，1か月後の体重をおおよそ知ることができるようになるわけです。このような，ある変数（1か月後の体重）の値を別の変数から予測（説明）する式のことを回帰式や回帰モデルと呼びます。

この式において，式の左辺にある変数（1か月後の体重）は従属変数や目的変数この従属変数を予測，説明するために用いられる変数（毎日のウォーキング時間）は予測変数や説明変数などと呼ばれます。回帰分析においては，説明される側の変数（従属変数）は1つ，説明する側の変数（予測変数）は1つまたは複数です。予測変数が1つの場合を単回帰分析，複数ある場合を重回帰分析と呼んで区別することもあります。

なお，先ほどの回帰モデルは，一見すると予測変数が2つあって重回帰分析のモデルのように見えるかもしれません。しかし，この式で毎日のウォーキング時間を長くしたり短くしたりしてその影響を見た場合，ウォーキング時間はそのつど値が変化しますが，現在（ダイエット開始時）の体重はすでに決まっていて変わることがありません（定数）。そのため，このモデルの予測変数は「毎日のウォーキング時間」のみであり，これは単回帰分析のモデルということになるのです。

この回帰式を，もう少し一般化した形で書くと次のようになります。

\[ 従属変数 = b_0 + b_1 \times 予測変数 \]

この\(b_0\)の部分は切片，\(b_1\)の部分は回帰係数と呼ばれます。先ほどの式の「現在の体重」は，この切片に相当する部分です。回帰分析でとくに重要なのは「回帰係数」で，これが従属変数に対する予測変数の影響力の強さや向きを表します。

また，予測変数が複数ある重回帰分析の場合には，回帰式は次のような形になります。

\[ 従属変数 = b_0 + b_1 \times 予測変数_{1} + b_2 \times 予測変数_{2}+ \cdots + b_n \times 予測変数_{n} \]

この式の場合，\(b_1\)から\(b_n\)の部分はとくに偏回帰係数と呼ばれます。これらの値は偏相関係数と同様に他の変数の影響を除外して算出されており，それぞれの予測変数が単独で持っている影響力の強さや向きを示しています。

なお，回帰分析にはいくつかの手法があり，従属変数と予測変数の間にピアソンの相関係数で捉えることができるような直線的な関係（線形関係）があることを想定したものをとくに線形回帰と呼びます。

7.3.2 基本手順

それでは回帰分析の手順を見ておきましょう。ここでも，サンプルデータは相関行列のところで用いたのと同じデータ（regression_data01.omv）を用います。（線形）回帰分析を実行するには，分析タブの「 inline 回帰分析」から「線形回帰」を選択してください（図7.23）¹。

図7.23: 線形回帰

すると，図7.23のような画面が表示されます。非常にたくさんの項目がありますので，まずは大まかな項目について見ておきましょう。

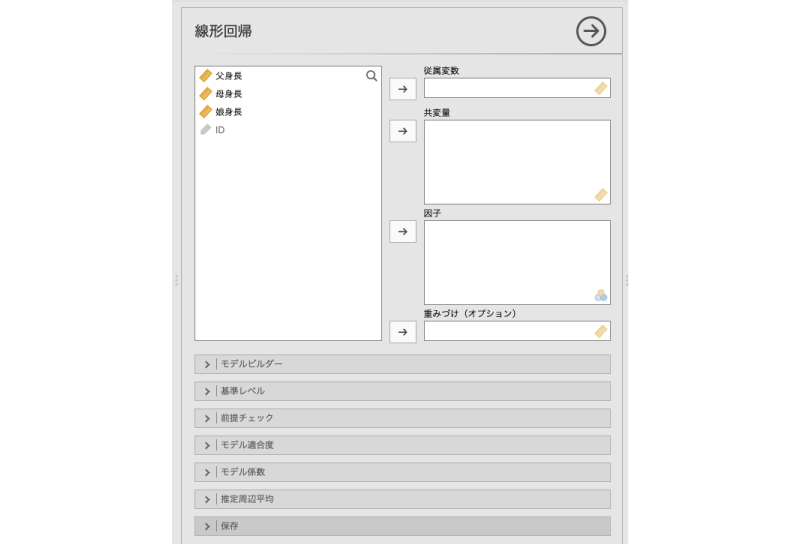
図7.24: 線形回帰の設定画面

従属変数　回帰分析に使用する従属変数を指定します。
共変量　回帰分析に使用する予測変数のうち，連続型のものを指定します。
因子　回帰分析に使用する予測変数のうち，名義型のものを指定します。
重みづけ（オプション）　線形回帰で重みづけを行う場合に使用します。
| モデルビルダー　交互作用を含むモデルの作成や複数モデルの比較を行います。
| 基準レベル　比較基準として用いる水準値を指定します。
| 前提チェック　正規性の検定など，分析の前提条件をチェックします。
| モデル適合度　モデル適合度に関する設定を行います。
| モデル係数　モデル係数に関する設定を行います。
| 推定周辺平均　各主効果の周辺平均値（回帰モデルによる推定値）に関する設定を行います。
| 保存　モデル予測値や残差などを新たな変数として保存します。

単回帰

ここでは，「父身長」から「娘身長」をどの程度説明できるのかについて分析してみます。その場合，分析の「従属変数」は「娘身長」，「予測変数」は「父身長」です。線形回帰分析では，分析の従属変数にあたる変数を「従属変数」に，そして予測変数として用いる変数は「共変量」または「因子」に設定します。

「共変量」と「因子」の違いは，その予測変数が「連続型（ inline ）」の変数であるか，「名義型（ inline ）」の変数であるかです。そのことは，変数指定欄の右下のアイコンからもわかります。回帰分析に用いる予測変数は連続型（比率尺度や間隔尺度）である場合が一般的ですが，性別などの名義変数を予測変数として用いることもできるのです。

今回の分析では予測変数は父親の身長で，これは連続型変数ですから，「父身長」は「共変量」の欄に移動します（図7.25）。

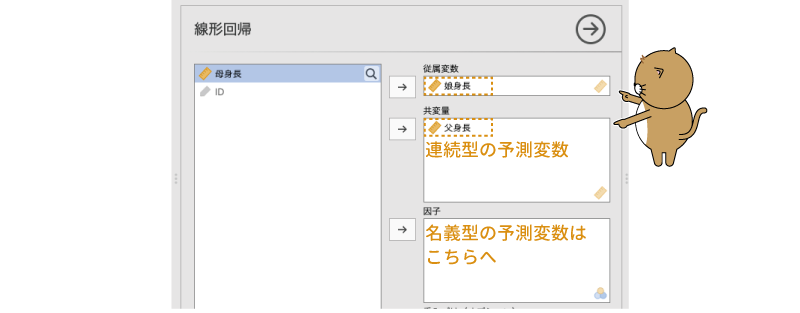
図7.25: 線形回帰の分析設定

なお，その下にある「重みづけ（オプション）」の欄は，重みつき回帰や重みつき最小2乗法と呼ばれる方法で回帰分析を実施する場合に使用します。重みつき回帰については本書では扱いませんが，これは回帰モデルの残差が予測値にかかわらず一定であるという回帰分析の前提（「前提チェック」を参照）が満たされない場合などに，残差に適切な重みづけを行って線形回帰を行う手法です。重みづけの値が入力された変数がある場合には，その変数をこの「重みづけ（オプション）」の欄に指定しますが，「オプション」とあるように，ここは通常は空欄のままで構いません。

これで基本的な分析は終了です。出力ウィンドウの結果は図7.26のようになっているはずです。

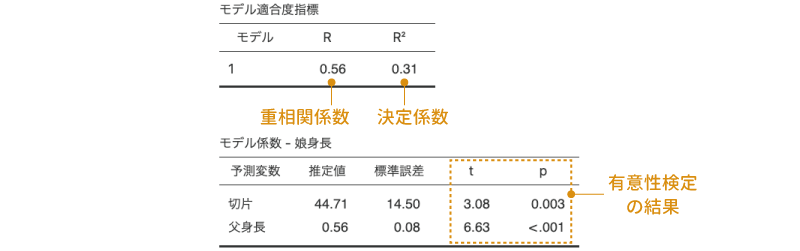
図7.26: 線形回帰の分析結果

結果の表のうち，最初の「モデル適合度指標」の部分には，分析に使用した回帰モデルが従属変数をどの程度うまく説明できているかについての情報が示されています。「モデル」の部分の数値（「1」）はモデルの番号です。複数のモデルを作成して比較する場合にはそれぞれのモデルを区別するために番号が用いられますが，ここではモデルを1つしか用いませんので，この数字は無視して構いません。

この表の「R」の部分は，このモデルによる予測値と実際の測定値（「娘身長」）の間の相関係数で，これは重相関係数と呼ばれています。今回の分析モデルのように，予測変数が1つしかない場合には，この重相関係数は「娘身長」と「父身長」の相関係数に一致します。その右の「R²」は決定係数と呼ばれ，これは0から1までの値をとります。この値は，「娘身長」の分散のうち，この回帰モデルで説明可能なものの割合，つまりこのモデルの「娘身長」に対する説明率を示しており，R²が0.31であるということは，このモデルで「娘身長」の分散の31%を説明できるということを意味しています。当然ながら，この値はできるだけ大きいことが望まれます。

この決定係数（R²）の値は，一般には次の式によって算出されます。

\[ R^2 = \displaystyle\frac{\text{予測値の平方和}}{\text{従属変数の平方和}} \]

このようにして算出する場合，決定係数の値は重回帰係数を2乗した値に一致します。

2つ目の表には，切片や予測変数に関する情報が示されています。この表の「推定値」の列が切片の値と予測変数の回帰係数の値です。この分析結果から，切片の値は44.71，「父身長」の回帰係数は0.56であることがわかります。これを回帰式の形にすると，次のようになります。

\[ \text{娘身長} = 44.71 + 0.56 \times \text{父身長} \]

この回帰係数の値は，父親の身長が1cm変化した場合に娘の身長がどの程度変化するかを意味します。つまり，この分析結果から，父親の身長が1cm高くなれば，娘の身長は0.56cm高くなるということがいえます。

その右隣の「標準誤差」の列には，これらの推定値の標準誤差が示されています。先ほどの切片の値や回帰係数はあくまでも推定値ですから，そこにはある程度の誤差のあることが考えられます。そしてその誤差の大きさについての指標がこの標準誤差です。さらに，この標準誤差に基づいて，それぞれの値が実際には0である可能性がないかどうかを検定した結果が「t」および「p」の部分です。この表の「t」の部分には，「母集団における実際の値は0である」という帰無仮説に対する検定統計量tの値が示されています。そして，このtの値に対する有意確率pがその隣の「p」の欄です。このpの値が有意水準を下回る場合に，回帰係数が有意である（0でない）と判断します。

なお，この場合の回帰モデルにおいては，切片の値は帳尻合わせのような役目しかありませんので，この値が0であるかどうかは分析の関心とはなりません。この場合，重要なのは父親の身長による影響力の部分です。この分析結果では，「父身長」の回帰係数についての検定結果は「p<.001」ですので，娘の身長に対する父親の身長の影響力は有意であるといえます。ただし，この検定はあくまでも回帰係数が「0でない」かどうかについてのものですので，この検定結果が有意であったからといって，「影響力が大きい」というわけではないという点には注意してください。影響力の大きさは，回帰係数の推定値で判断する必要があります。

重回帰

今度は父親の身長だけでなく，父親と母親の両方の身長による影響について見てみましょう。分析手順は，基本的に先ほどの場合と同じです。分析タブの「 inline 回帰分析」から「線形回帰」を選択し，表示された設定画面の「従属変数」に「娘身長」，「共変量」に「父身長」と「母身長」を指定します（図7.27）。

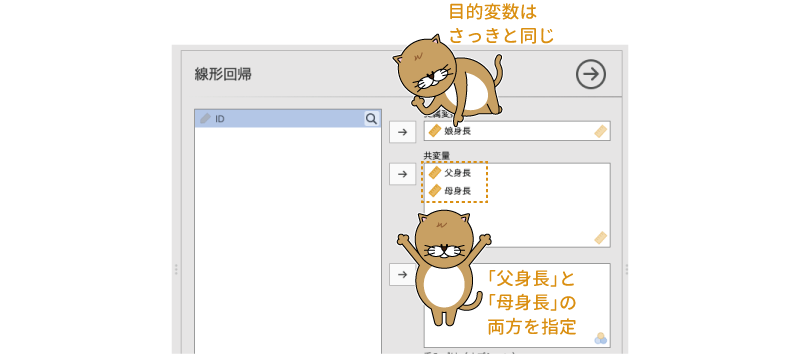
図7.27: 複数の予測変数を用いた分析

すると，「父身長」と「母身長」のそれぞれについて回帰係数が算出されます（図7.28）。

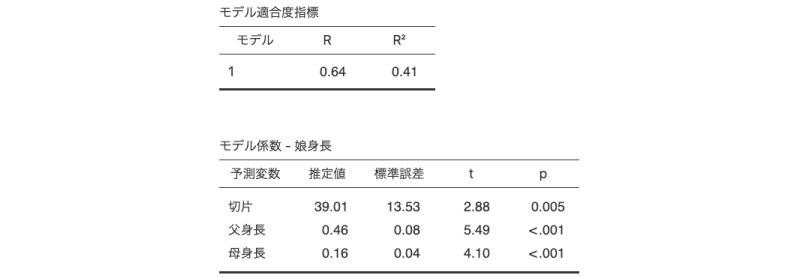
図7.28: 重回帰分析の分析結果

先ほどの「父身長」のみを予測変数とする単回帰分析の結果に比べ，決定係数（R²）は0.41と若干ですが大きくなっています。複数の予測変数を用いたことでモデルの複雑性が増し，「娘身長」の分散をより多く説明できるようになったのです。

重回帰分析における各予測変数の回帰係数は，とくに偏回帰係数と呼ばれます。この分析結果では，「父身長」の回帰係数は0.46で，単回帰の場合の回帰係数の0.56よりも少し小さくなっています。この場合の「父身長」の回帰係数は偏回帰係数で，これは「父身長」以外（ここでは「母身長」）の値を固定した場合の「父身長」の影響力を表しています。つまり，母親の身長が同じ家族の中では，父親の身長が1cm高くなると娘の身長が0.46cm高くなるということです。「母身長」の回帰係数についても同じで，父親の身長が同じ家族だけをみた場合に，母親の身長が1cm高くなれば，娘の身長は0.16cmだけ高くなるということになります。

7.3.3 モデルビルダー

一般に，予測変数が複数ある重回帰モデルは，予測変数が1つしかない単回帰モデルに比べ，従属変数の分散についてより多くを説明することができます。しかし，それなら予測変数を増やせるだけ増やしたほうがいいかというと，そうではありません。予測変数が多くなればなるほどモデルは複雑化し，変数間の影響関係を理解することが困難になってしまうからです。つまり，重回帰分析を行う場合には，できるだけ予測変数が少なくシンプルで，かつ従属変数の分散をできるだけ多く説明できるモデルが好ましいのです。

先ほどの分析では，「母身長」の回帰係数は「父身長」の回帰係数に比べて小さな値でした。ということは，もしかしたら娘の身長を説明するには父親の身長がわかっていれば十分で，母親の身長を予測変数として用いる必要はなかったかもしれません。だとすると，父親と母親の両方の身長を予測変数として用いた回帰モデルは不必要に複雑なものだということになってしまいます。

ではこの場合，父親の身長のみを用いたモデルと，父親と母親の身長の両方を用いたモデルのどちらを採用するのがよいのでしょうか。jamoviに搭載されている「モデルビルダー」は，そうした判断を行う場合に便利な機能です。モデルビルダーでは，複数のモデルの間で比較を行い，モデルに使用する予測変数の選択を行うことができます。

それでは，モデルビルダーを用い，父親の身長のみの回帰モデルと父親と母親の身長を用いた回帰モデルの間で比較を行ってみましょう。先ほどの「父身長」と「母身長」を予測変数として用いた回帰分析の結果をクリックし，分析設定画面を再度開いてください。そして，その設定画面の| モデルビルダーの部分を展開すると，次のような画面が現れます（図7.29）。

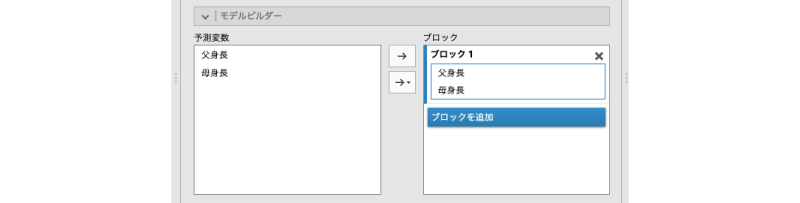
図7.29: モデルビルダー

画面左側の「予測変数」には，この回帰分析で用いられている予測変数の一覧が表示されています。そして右側の「ブロック」の部分にも，先ほど分析に使用した予測変数が表示されています。

ここでまず，「ブロック1」のところにある「母身長」を選択し，「 inline 」をクリックして「ブロック1」の部分から「母身長」を削除します（図7.30）。

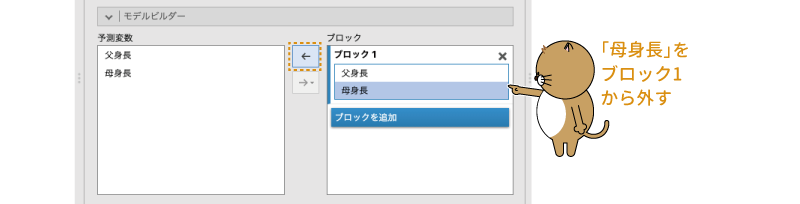
図7.30: 「母身長」をブロック1から削除

次に，ブロックを追加をクリックして，新たなブロックを作成します（図7.31）。

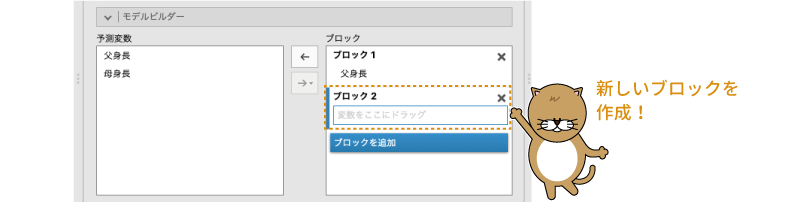
図7.31: 新たなブロックを作成

そして，先ほどブロック1から削除した「母身長」を，新しく作成した「ブロック2」にマウスでドラッグして移動します（図7.32）。

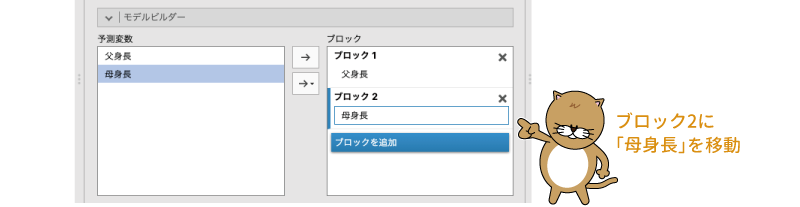
図7.32: 「母身長」をブロック2に追加

ここまでの設定を行ったら，分析結果を見てみましょう。分析結果は図7.33のようになっているはずです。

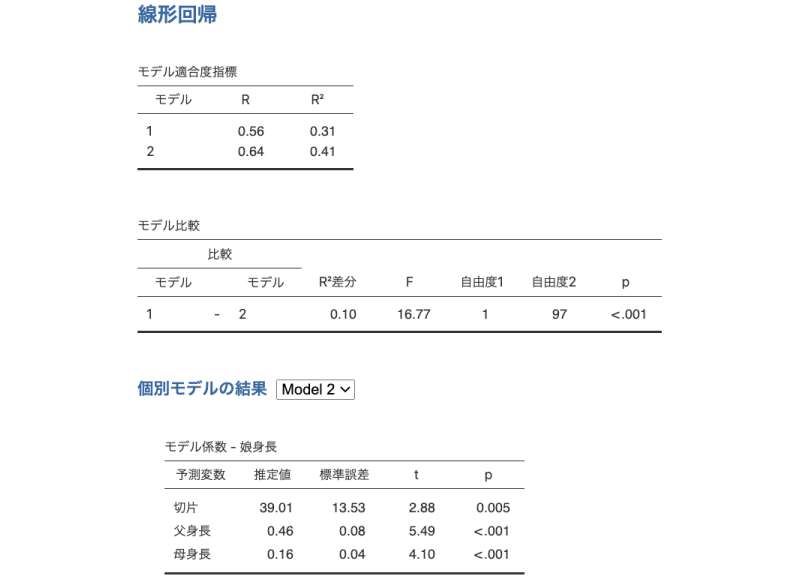
図7.33: モデルビルダーの出力結果

1つ目の「モデル適合度指標」の表には，モデルビルダーの「ブロック1」に指定した予測変数のみを用いたモデル（モデル1）の適合度（重相関係数Rおよび決定係数R²）と，そこに「ブロック2」に指定した予測変数を加えた場合（モデル2）の適合度が示されています。つまり，このモデル1は「父身長」のみを予測変数とする回帰モデル，モデル2は「父身長」と「母身長」を予測変数とする回帰モデルの分析結果です。

ですから，これらの数値はそれぞれ，「父身長」のみを予測変数として行った単回帰分析の結果（単回帰参照）や，「父身長」と「母身長」を予測変数として行った重回帰分析の結果（重回帰参照）と同じ値です。

2つ目の「モデル比較」の表は，この2つの回帰モデルの精度を比較した結果です。この表の「比較」の部分には，比較対象となっているモデル（ここではモデル1とモデル2）が，「R²差分」の部分には2つのモデルで決定係数がどれだけ異なるかが示されています。そしてこの結果から，予測変数が「父身長」のみのモデル1に比べ，予測変数として「父身長」と「父身長」の2つを用いたモデルのほうが，決定係数が0.10だけ大きいということがわかります。

その横の「F」から「p」までの部分は，この決定係数の増加分が「0でない」かどうかについての検定結果です。表の中のFの値は，モデル1では説明しきれずモデル2によって新たに説明される部分の分散を，モデル2の残差の分散で割って求められます。「自由度1」はモデル2とモデル1の予測変数の個数の差，「自由度2」はモデル2の残差自由度です。

そして，表の一番右端の有意確率pの値が有意水準を下回っている場合には，モデル1とモデル2の説明率の差が0ではない（「母身長」を予測変数に追加することが無駄ではない）ということになります。この分析結果では有意確率はp<.001ですので，「母身長」を予測変数に加えることによって回帰モデルの説明率が有意に向上したということができます。

この表の下の「個別モデルの結果」の部分にある表は，比較したモデルのうちの1つについての分析結果です。このタイトル部分の横にあるプルダウンメニューで，どのモデルの結果を表示させるかを選択することができます。この画面では「モデル2」の結果，つまり「父身長」と「母身長」の両方を予測変数とする重回帰分析の結果が表示されています。

交互作用を用いた回帰分析

重回帰分析では，それぞれの変数を個別に予測変数として用いるだけでなく，分散分析の場合と同様に，いくつかの予測変数間の交互作用を予測変数として用いることもできます。複数の予測変数による交互作用を回帰モデルに含める場合には，モデルビルダーで設定を行います。

先ほどの回帰モデルに，さらに「父身長」と「母身長」の交互作用を追加してみましょう。分析結果をクリックし，| モデルビルダーの「ブロック」に3つ目のブロックを追加してください（図7.34）。

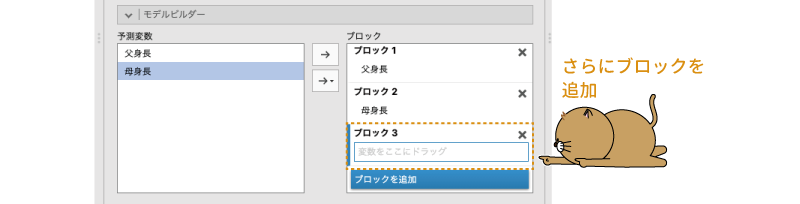
図7.34: モデルビルダーで3つ目のブロックを作成

そして，画面左側の「予測変数」の部分で「父身長」と「母身長」の2つを選択します²。そして「予測変数」と「ブロック」の間にある2つの「 inline 」ボタンのうち，下にあるほうをクリックすると，図7.35のように選択メニューが表示されますので，そこから「交互作用」を選択してください。

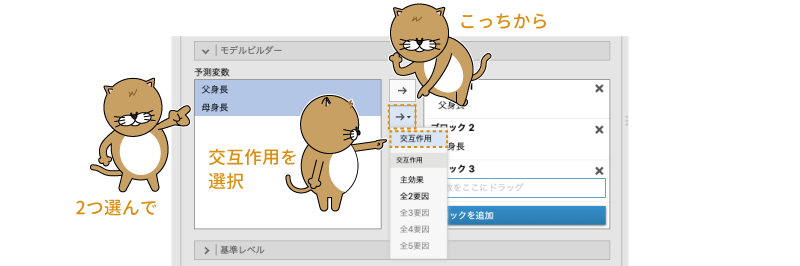
図7.35: モデルビルダーで3つ目のブロックを作成

すると，次のように「ブロック3」の部分に「父身長＊母身長」という項目が追加されます（図7.36）。これが交互作用項です。

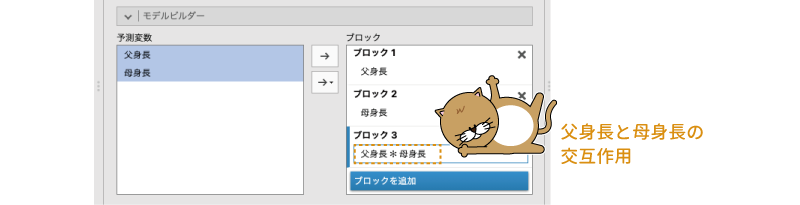
図7.36: 3つ目のブロックに交互作用を設定

なお，「予測変数」と「ブロック」の間に似たような「 inline 」ボタンが上下に2つ並んでいますが，下にあるほう（右側に小さな三角があるもの）は，このように選択した変数の主効果（つまり交互作用なし）や交互作用を個別に指定してモデルに追加するためのボタンです。これに対し，上にあるほうの「 inline 」ボタン（小さな三角がないもの）は，選択された変数の主効果とすべての交互作用の組み合わせをモデルに追加します（図7.37）。

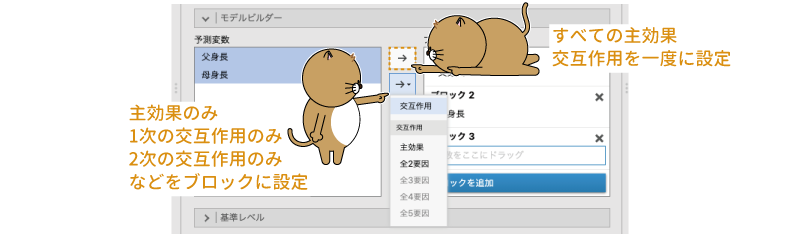
図7.37: ボタンの役割の違い

ただし，すでに先のブロックでモデルに追加されている変数や交互作用項を後のブロックで重ねて追加することはできませんので，そのような変数や交互作用がある場合には，それらは新しいブロックには追加されません。

では結果を見てみましょう。基本的な結果の見方は先ほどと同じですので，ここではとくに，2つ目の表（モデル比較）に注目して見ておきます（図7.38）。

図7.38: モデルの比較

この表には，モデル1とモデル2の比較，そしてモデル2とモデル3の比較が示されています。この分析結果では，モデル1とモデル2の説明率の差は有意，つまり予測変数が「父身長」のみのモデルに「母身長」を加えればモデルが有意に向上しますが，モデル2とモデル3の間では差は有意ではありません。ということは，モデル2にさらに「父身長」と「母身長」の交互作用を加えてもモデルの説明率は有意には向上しない，つまり「娘身長」の値を説明する上で，「父身長」と「母身長」の交互作用は必要ないということになるのです。このようにして，関心のある変数や交互作用項を段階的に回帰分析モデルに投入していき，モデルの説明率が有意に増加するかどうかを確認して最適なモデルを選択する方法は，階層的重回帰分析とも呼ばれます。

なお，先ほどの分析結果では「父身長＊母身長」は有意ではありませんでしたが，もしこの交互作用の回帰係数が\(-\textsf{2.15}\)のような値で有意になっていたとすると，それは「父親の身長が高ければ高いほど（低ければ低いほど），娘の身長に対する母親の身長の影響力が小さくなる（大きくなる）」という関係があることを意味します。

このような2変数間の交互作用であれば解釈可能かもしれませんが，これが3変数間，4変数間の交互作用になったらどうでしょうか。おそらくほとんど解釈できなくなってしまうでしょう。交互作用を解釈できなければ，当然ながら交互作用が有意であった場合の分析結果を理解することもできません。このように，回帰分析における交互作用項は一般に解釈が困難になりがちですので，回帰モデルに交互作用を含めるかどうかはよく考えてから判断するようにしましょう。

7.3.4 基準レベル

今度は別のデータで回帰分析を行ってみましょう。次のサンプルデータ（regression_data02.omv）をダウンロードして開いてください。このデータファイルは，先ほどと同じく100家族分の身長データなのですが，父母の身長と子供の身長，そしてその子供の性別が記録されています（図7.39）。

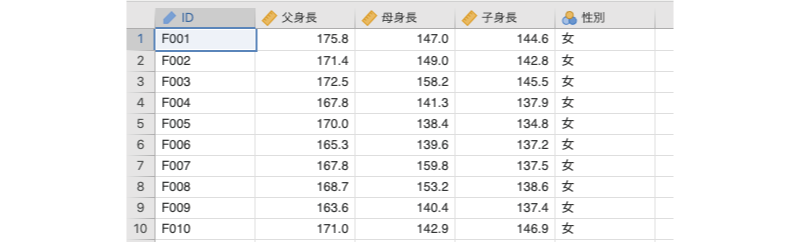
図7.39: サンプルデータ2

ID　対象家族のID
父身長　父親の身長（単位：cm）
母身長　母親の身長（単位：cm）
子身長　子供の身長（単位：cm）
性別　子供の性別（男，女）

このデータを用いて，子供の身長が父親・母親の身長と子供の性別という3つの変数からどのように説明できるかを見てみたいと思います。

まず，分析タブの「 inline 回帰分析」から「線形回帰」を選択し，表示された設定画面の「従属変数」に「子身長」，「共変量」に「父身長」と「母身長」を指定します（図7.40）。ここまでは，従属変数の名前が違うこと以外は，先ほどの分析とまったく同じです。

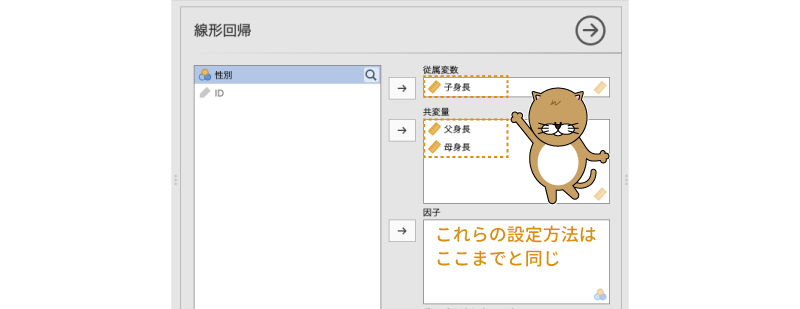
図7.40: 連続型予測変数の設定

次に，「性別」変数ですが，この変数は名義尺度変数ですので，これは「因子」へ移動します（図7.41）。

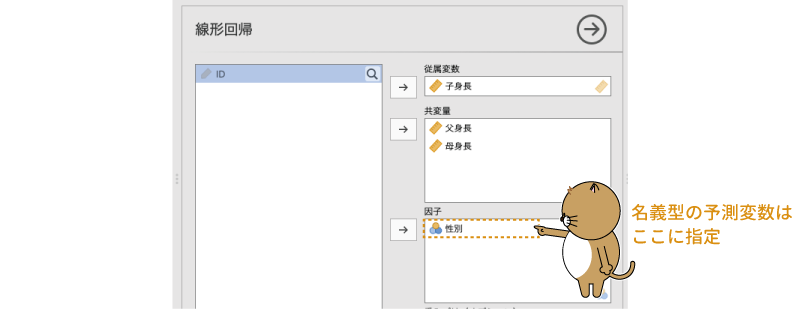
図7.41: 名義型予測変数の設定

すると，図7.42のような結果が得られます。

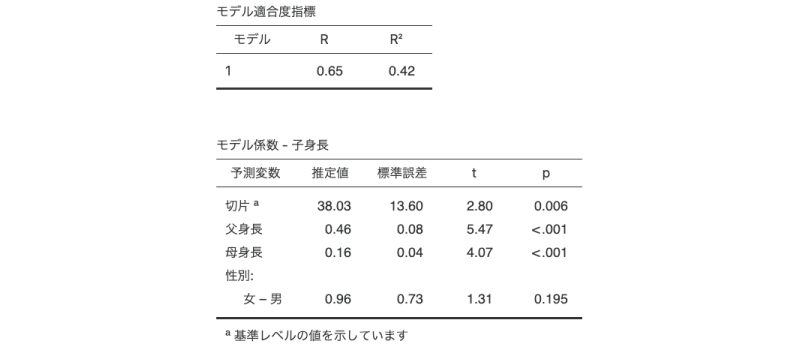
図7.42: 名義型予測変数を含む回帰分析の結果

この結果は基本的にはこれまでの重回帰分析のものと同じなのですが，最後の「性別」の行が少し特殊な形になっています。この「性別：女 - 男」の行は，子供の性別が「女」の場合に身長が平均的にどの程度変化するかを示しています。つまり，子供が女の子の場合には，平均して男の子よりも身長が0.96cm高くなるということなのです。

このような名義型の予測変数の場合には，男の子の身長を基準にするか，女の子の身長を基準にするかによって，表現の仕方が異なってきます。男の子の身長を基準に考えれば，女の子のほうが0.96cm背が「高い」ということになりますが，女の子の身長を基準に考えると，男の子のほうが女の子より0.96cm背が「低い」ということになるからです。

今回の分析ではどちらの表現であっても構わないと思いますが，もし「男の子の身長」のほうに関心があって，それに対する予測変数の影響を知りたい場合には，この結果のような「女の子の場合，男の子に比べて身長が平均で0.96cm高くなる」という形よりも，「男の子の場合，女の子に比べて……」という表現のほうがわかりやすいでしょう。そのような場合には，分析設定画面の| 基準レベルの項目で，基準となる変数値を指定することができます。

先ほどの回帰分析の結果をクリックし，分析設定画面を再度開いてください。そして，その設定画面の| 基準レベルを展開すると，図7.43のような画面が現れます。

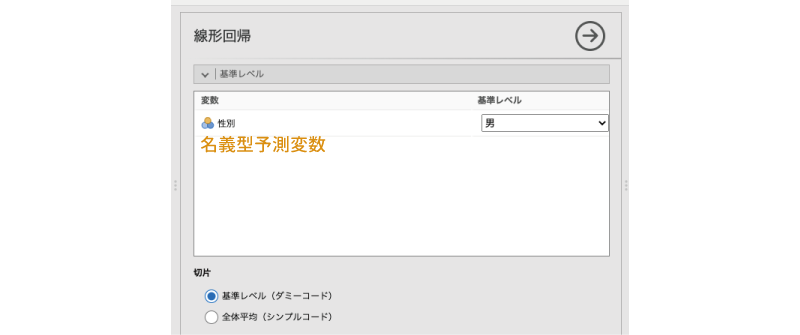
図7.43: 名義型予測変数の基準レベルの設定

変数　名義型予測変数の一覧です。
基準レベル　回帰係数を算出する際の基準レベルを指定します。
切片　切片の計算方法を指定します。
- 基準レベル（ダミーコード）　基準レベルを0，それ以外を1の形に数値化します。
- 全体平均（シンプルコード）　変数値の平均が0になるように数値化します。

この画面の「Variable（変数）」欄には，この分析に用いられている名義型の予測変数が一覧表示されます。そして，その右側の「Reference Level（基準レベル）」で，それぞれの名義型変数について，どの値を基準に値を算出するかを指定することができます。

ここでは「男」が基準となっていますが，ここを「女」に変更すると，女児の身長が比較の基準となり，結果の表示は「男の子の場合，女の子に比べて……」という形になります。「基準レベル」の部分を「女」に設定してみましょう。すると，結果は図7.44のようになります。

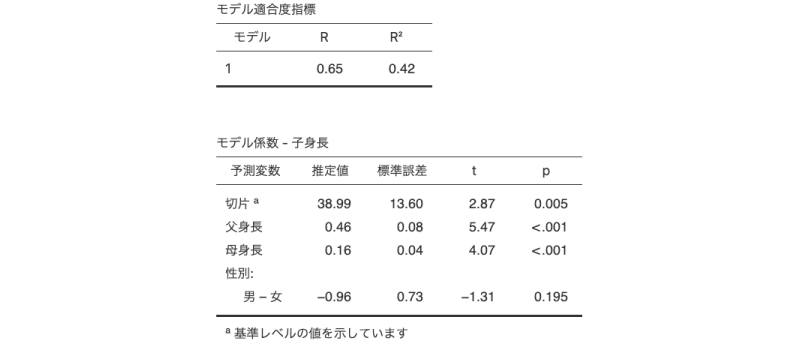
図7.44: 女児の身長を基準とした回帰分析の結果

「性別」の回帰係数の符号（\(+/-\)）が逆になっているのがわかるでしょうか。この場合，「女の子の身長」という基準に対し，「男の子の身長」はそれよりも平均して0.96cmだけ低くなるという意味になります。

切片

なお，| 基準レベルの下のほうにある「切片」の部分では，名義型変数を回帰分析に用いる際の処理方法についての設定が可能です。，一般に，回帰モデルの予測変数に「性別」のような名義型の変数が含まれている場合には，基準とする値を「0」，比較する側の値を「1」に置き換えるダミーコード化（ダミーコーディング）という方法がとられます。たとえば，係数を算出する際の基準が「男」であれば，性別の値が「男」の場合を「0」，「女」の場合を「1」と置き換えたうえで計算を行うのです³。

基準レベル（ダミーコード）

この「切片」が「基準レベル（ダミーコード）」に設定されている場合には，基準となる値を「0」，それと比較する側の値を「1」として回帰係数の算出を行います。この方法では，どちらを基準とするかによって，名義型変数に対する回帰係数の符号が変わるだけでなく，切片の値も変化します。先ほどの分析結果で，「男」を基準にした場合と「女」を基準にした場合の結果を見比べてみてください。「女」を基準とした場合のほうが，切片の値が0.96だけ大きくなっているはずです。

全体平均（シンプルコード）

これに対し，「切片」が「全体平均（シンプルコード）」に設定されている場合には，基準となる値を「\(-\textsf{0.5}\)」，それと比較する側の値を「0.5」などとして，2つの変数値の平均値が0になるように数値化したうえで回帰係数の算出を行います。この方法では，どちらを基準にした場合にも切片の値は変化しません。変わるのは，名義型変数に対する回帰係数の符号だけです。なお，この場合の切片の値は，ダミーコード化して算出される2種類の切片の平均値と同じ値になります。

先ほどの分析結果の表の下に「ª 基準レベルの値を示しています」や「ª 全体平均の値を示しています」という注釈があったのはこのためです。予測変数に名義型変数が含まれる回帰分析では，このように計算方法によって切片の値が異なってきますので，その点には注意してください。

7.3.5 前提チェック

t検定や分散分析のように，回帰分析にも分析における前提条件がいくつかあります。それらの前提条件が満たされているかどうかは，分析設定画面の| 前提チェックの部分にある項目を用いて確認できます（図7.45）。

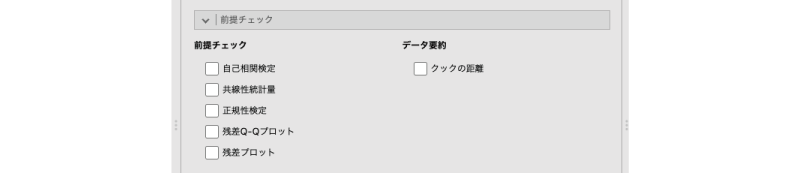
図7.45: 回帰分析の前提チェック

前提チェック　回帰分析の前提条件が満たされているかどうかをチェックするための項目です。
- 自己相関検定　自己相関の有無について検定します。
- 共線性統計量　多重共線性の問題が生じていないかどうかを確かめます。
- 正規性検定　残差の正規性について検定を行います。
- 残差Q-Qプロット　残差のQ-Qプロットを作成します。
- 残差プロット　残差のプロットを作成します。
データ要約
- クックの距離　各測定値についてクックの距離を算出します。

t検定や分散分析では，分析の前提条件として，分析対象となる従属変数の分布が正規分布からかけ離れていないか，グループ間で分散が極端に異なっていないかなどが問題となりました。回帰分析の場合，回帰モデルによる予測値と従属変数の間の「残差」や，分析に使用する予測変数について，いくつかの前提条件が存在します。

自己相関検定

回帰分析には，「残差が互いに独立である」という前提があります。「残差が独立」であるとは，各測定値の残差が不規則な値をとっており，そこに特定のパターンが見られないということです。そして，この残差の分布の仕方に特定のパターンが見られないかどうかを確認する方法の1つに，残差の自己相関検定があります。

たとえば時系列データ⁴の場合，ある時点における測定値は，その直前・直後の測定値と似通った値になりがちです。このように，変数値のならびによって測定値間に相互に関連が見られるような状態を自己相関あるいは系列相関といいます。残差に自己相関が見られる場合，決定係数R²が実際より大きな値になってしまうといった問題が生じます。

残差の間に自己相関が見られないかどうかを確かめる方法としてよく用いられるのがダービン・ワトソン検定です。回帰分析の前提チェックで「自己相関検定」のチェックをオンにすると，自己相関の検定としてこのダービン・ワトソン検定の結果が表示されます（図7.46）。

図7.46: 自己相関検定の結果

結果の表の「自己相関」の部分が自己相関係数，「DW統計量」の部分がダービン・ワトソン比（DW比）と呼ばれる値です。この値が2に近づくほど自己相関が弱く，2より大きい，あるいは小さいほど自己相関が強いことを意味します。表の一番右端のpは，このダービン・ワトソン比についての有意確率で，この値が有意水準より小さい場合に残差に自己相関があると判断されます。

共線性統計量

重回帰分析に用いられる予測変数は，多くの場合，お互いにある程度の相関関係にあるものです。しかし，その関係が強すぎる場合，つまり分析に使用される予測変数の中に強い相関関係にある変数が含まれている場合には，回帰係数が本来の関係とは逆の符号になってしまったり，決定係数の値が適切に算出できなくなったりなど，回帰分析の結果が不安定になることが知られています。このような，複数の予測変数の間に強い相関関係がある状態を多重共線性といい，多重共線性の問題がある場合には，回帰分析の結果は信頼できないものになってしまうのです。

こうした問題が生じていないかどうかを確かめるには，回帰分析の前提チェックで「共線性統計量」のチェックをオンにします。すると，図7.47のような形で多重共線性の指標が表示されます。

図7.47: 分散拡大係数とトレランス

この表の「VIF」の値は，分散拡大係数と呼ばれるもので，多重共線性の強さを示す指標としてよく用いられています。このVIFの値が大きいほど多重共線性が強く見られることを意味しており，この値が5を超えるような予測変数⁵は，分析から除外するなどの何らかの対策をとる必要があります。

また，その隣の「トレランス」は，VIFの逆数（1/VIF）です。トレランスは，小さければ小さいほどその予測変数の多重共線性が強いことを意味します。

正規性検定

回帰分析における主要な前提条件の1つに，残差が正規分布であることというものがあります。回帰分析の残差は単に独立であるだけでなく，正規分布に近いものでなければならないのです。

回帰分析において残差の正規性を確認するための方法にはいくつかのものがありますが，そのうちの1つがシャピロ=ウィルク検定です。回帰分析の前提チェックで「正規性検定」のチェックをオンにすると，回帰モデルの残差についてのシャピロ=ウィルク検定の結果が表示されます（図7.48）。

図7.48: シャピロ=ウィルク検定

シャピロ=ウィルク検定の値の見方は第4章で見たのと同じです。検定統計量が1に近いほど正規分布からのずれが小さく，0に近いほど正規分布からのずれが大きいことを意味します。表の右側に示されている有意確率pの値が有意水準を下回る場合に残差が正規分布していないと判断されます。

残差Q-Qプロット

残差の正規性については，グラフを用いて視覚的に判断する方法もあります。回帰分析の前提チェックで「残差Q-Qプロット」にチェックを入れると，出力ウィンドウに残差のQ-Qプロットが表示されます（図7.49）。こちらも第4章で説明したように，各データ点が直線上に並んでいれば残差が正規分布しており，そうでなければ正規分布でないと判断されます。

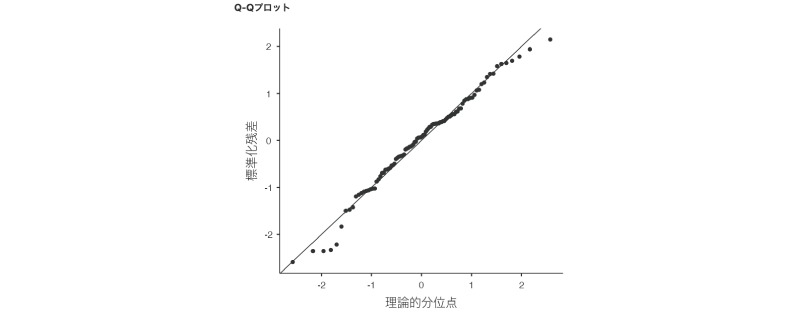
図7.49: 残差Q-Qプロット

残差プロット

回帰分析の残差は，互いに独立であること，正規分布からかけ離れていないことの他に，その分布の幅が予測値にかかわらず一定であることが必要とされます。残差の分布に何らかの特徴的な傾向が見られる場合，回帰分析の結果が妥当でない可能性があります（図7.50）。

図7.50: 残差の傾向の有無

残差に何らかのこうした特徴的な傾向が存在しないかどうかを確認するためには，回帰分析の前提チェックで「残差プロット」のチェックをオンにします。こうすることで，残差のばらつきをさまざまな形で視覚化して確認することができます。

この残差プロットで図7.50の右の図ように残差の分布に特徴的な傾向が見られる場合，対処方法の1つとして，線形回帰の「重みづけ（オプション）」の欄に適切な重みづけ変数を設定して「重みつき回帰」を行うことが考えられます。

この残差プロットの1つ目のグラフ（図7.51）は，回帰モデルによる予測値と残差の関係を示したものです。このグラフ上の点が，グラフの左側から右側まで，縦軸の0の値を中心に同じような幅で上下に散らばっていれば，予測値に関係なく残差の分散に偏りはないといえます。グラフを見る限り，予測値と残差の間に特別な関係はなさそうです。

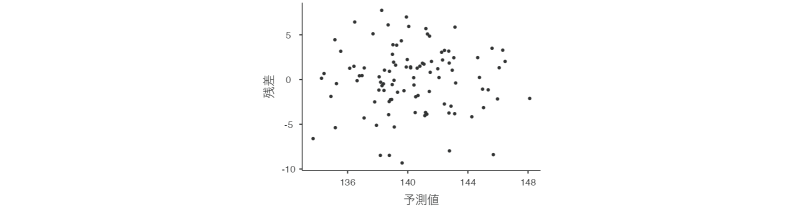
図7.51: 予測値と残差の散布図

残差プロットの2つ目のグラフ（図7.52）は，回帰モデルの従属変数と残差の関係を示したものです。このグラフ上の点が全体に円状に散らばっていれば，従属変数と残差の間に特定の関係は見られないといえます。なお，このグラフでは従属変数と残差の間にはっきりとした正の相関関係が見られますが，モデルの決定係数が0.9を超えるようなものでもない限り，従属変数と残差の間にこうした相関関係が見られるのは問題ではありません。

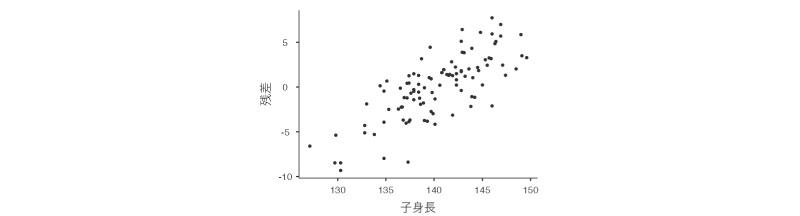
図7.52: 従属変数と残差の散布図

残差プロットの3つ目以降のグラフ（図7.53）は，各予測変数と残差の関係を示したものです。このグラフ上の点が全体に円状に散らばっていれば，それらの予測変数と残差の間に特別な関係は見られないということがいえます。このグラフを見る限り，これらの予測変数と残差の間には特別な関係は見られません。

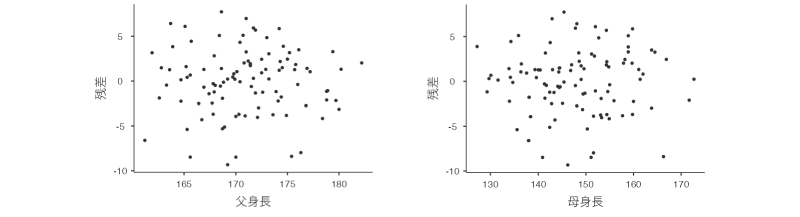
図7.53: 各予測変数と残差の散布図

データ要約

ピアソンの相関係数が外れ値の存在によって影響を受けやすいのと同様に，回帰分析においても外れ値による影響によって結果が歪められてしまう場合があります。回帰分析において外れ値による影響が見られないかどうかを確認する方法は，1つには先ほどのように残差プロットを作成し，残差のグラフの中に他からかけ離れた点がないかどうかを視覚的に確認することです。

クックの距離

回帰分析の結果を歪めるような外れ値の存在を視覚的にではなく数量的に確かめたい場合には，クックの距離と呼ばれるものがよく用いられます。クックの距離は，データ全体を用いた回帰分析の結果と，そのデータの中から特定の測定値を除外して行った回帰分析結果の間のずれを数値化したもので，クックの距離が大きい測定値がデータに含まれている場合には，その測定値が回帰分析の結果を歪めてしまっている可能性があります。一般に，クックの距離が0.5を超えるような値は影響が「大きい」とみなされ，この値が1を超えるような場合には，その影響が「とくに大きい」とみなされます。

クックの距離を算出するには，回帰分析の前提チェックで「データ要約」の部分にある「クックの距離」にチェックを入れます。すると，図7.54のような形で結果が表示されます。

図7.54: クックの距離

表として結果に示されるのは，各測定値についてのクックの距離の記述統計量（平均値，中央値と標準偏差，および最小値・最大値）のみですが，この後に触れる「保存」で設定を行うことによって，各測定値についてのクックの距離を新たな変数として保存することができます。クックの距離を新たな変数として保存すれば，分析結果に悪影響を及ぼしているデータ行がどれであるかを特定することもできるようになります。

7.3.6 モデル適合度

作成した回帰モデルの精度に関する指標としては「重相関係数（R）」や「決定係数（R²）」がよく用いられていますが，回帰モデルの精度（データへの適合度）に関する指標はこれ以外にも複数存在します。

回帰分析の設定画面で| モデル適合度の部分を展開すると図7.55のような画面が表示され，適合度に関する指標の設定を行うことができます。

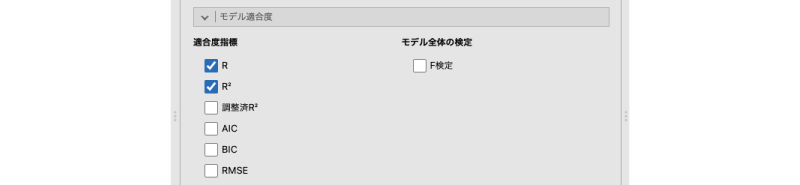
図7.55: モデル適合度

Fit Measures　モデル適合度の指標を指定します。
- R　重相関係数（R）を算出します。
- R²　決定係数（R²）を算出します。
- 調整済R²　調整済み決定係数（R²）を算出します。
- AIC　赤池情報量規準（AIC）を算出します。
- BIC　ベイズ情報量規準（BIC）を算出します。
- RMSE　誤差2乗平均平方根（RMSE）を算出します。
モデル全体の検定　全体的なモデル適合度についての検定を行います。
- F検定　予測変数を含まない帰無モデルと分析モデルに有意な差があるといえるかどうかについて検定を行います。

このモデル適合度の項目は，適合度指標に関する設定と，適合度の検定に関する設定の大きく2つの内容で構成されています。

適合度指標

回帰係数の適合度指標の1つである決定係数（R²）は，作成した回帰モデルによって従属変数の分散をどれだけ説明できるかを比率で表したものと解釈できます。つまり，決定係数が0.60であれば，その回帰モデルで従属変数の分散のうちの60%を説明できるということです。そのため，決定係数が高ければ，それだけ説明力のある，よいモデルということになります。また，重相関係数はモデルによる予測値と従属変数の実測値との間の相関係数であり，この重相関係数が1に近いほど，モデルが従属変数をよく説明できているということになります。また，一般に重相関係数を2乗した値は決定係数に一致します。

このように重相関係数や決定係数は非常に解釈の容易な指標なのですが，重回帰分析の場合，予測変数の個数が多くなるほど決定係数も大きくなる傾向にあるのです。そのため，これらの指標だけでモデルの良し悪しを判断すると，たくさんの予測変数が用いられた複雑なモデルのほうがよいモデルと判断されてしまうことになってしまいます。

しかし，これでは困ります。多変量解析を行うのは，多数の変数間の関係をできるだけ単純な形にしてわかりやすくすることが目的なわけですから，予測変数の個数が多く複雑なモデルほどよいということにはならないのです。回帰分析に求められているのは，できるだけシンプルで，かつ，できるだけ多くの情報を説明できるモデルだからです。

調整済R²

そこで重回帰分析の場合，モデルの良し悪しを判断する材料として，決定係数の大きさを予測変数の個数で調節した調節済決定係数（調整済みR²）あるいは自由度調整済決定係数と呼ばれる値がよく用いられています（図7.56）。この値は，予測変数の個数が多くなるほど決定係数に対して「ペナルティ」を与え，決定係数が大きくなりすぎないようにします。こうすることによって，不必要に多くの予測変数を含んだモデルのほうが適合度が高くなるということを防いでいるのです。心理学の研究論文では，重回帰分析の結果の報告の際には決定係数の代わりに調整済決定係数を用いることが多いようです。

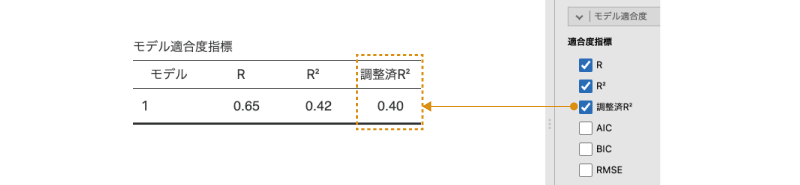
図7.56: 調整済決定係数

調整済決定係数は予測変数の個数によって調整された値であるため，調整されていない決定係数よりもわずかに小さな値になります。もし，調整されていない決定係数と調整済決定係数の値が大幅に異なるようであれば，不必要な予測変数がモデルに多数含まれている可能性が考えられます。

また，調整済決定係数では「従属変数の分散を○○%説明できる」というような解釈はできません。そうした解釈を行う場合には，調整されていないほうの決定係数を見る必要があります。

AIC，BIC，RMSE：モデル選択の指標

モデルの適合度を相対的に評価するための指標としてしばしば用いられるものに，赤池情報量規準（AIC）やベイズ情報量規準（BIC），があります。これらの値の算出方法についてはここでは触れませんが，これらの値は良好なモデル（少ない変数で多くを説明できる）ほど小さくなる性質があるため，複数モデルの中から良好なモデルを選択したい場合には，これらの指標が最小になるモデルを選択するようにします。

また，誤差2乗平均平方根（RMSE）も同様の指標で，この値は予測値と実測値の偏差2乗の平均値（つまり残差の分散）の平方根（つまり「残差の標準偏差」）です。モデルの予測精度が高いということは，それだけモデルの残差は小さくなるはずですから，この値が小さいほど，モデルの精度がよいということになります。なお，AICとBICは予測変数の個数を考慮して算出された値になっていますが，RMSEはそうでない点には注意が必要です。

なお，これらは相対的な比較のための指標であり，それ単独ではモデルの適合度がどの程度高いのかということまではわかりません。そのため，実際の分析場面では，これらの指標はモデルビルダーと組み合わせて使用するか，個別に作成したモデルの間で値の大小を比較したり変化量を見たりするかといった使い方が主になるでしょう（図7.57）。

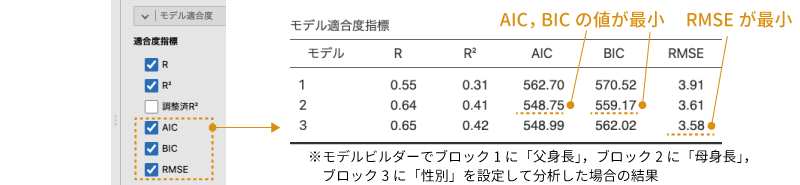
図7.57: モデル選択の指標

これらの適合度指標は，同じデータについて作成した複数のモデル間で適合度を比較することはできても，異なるデータについて作成されたモデル間で比較することはできません。また，AICやBIC，RMSEは，いずれか1つのみを用いることもありますが，複数の指標を用いて総合的にモデル評価を行うこともあります。

モデル全体の検定

モデルの適合度について，指標という形ではなく，十分適合しているといえるかどうかという形で判断したい場合もあるでしょう。その場合は，「モデル全体の検定」のところにある「F検定」のチェックをオンにします。

すると，図7.58のような結果がモデル適合度指標の横に表示されます。

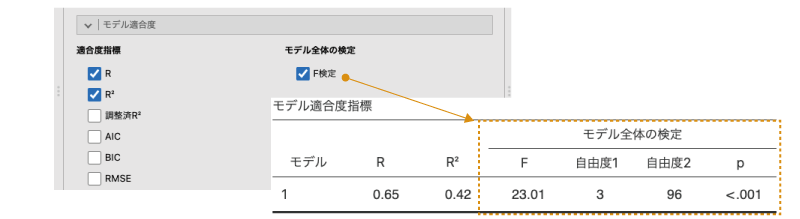
図7.58: モデル適合度の検定

モデルビルダーでは予測変数を追加することによる説明率の変化について検定を行いますが，ここでは切片のみのモデルと分析モデルの間で説明率が有意に向上したといえるかどうかについての検定を行います。したがって，表中のFの値は，切片だけでは説明しきれず，予測変数を用いることによって説明されるようになる分散を，分析モデルの残差の分散で割って求めた値です。「自由度1」は分析モデルにおける予測変数の個数（交互作用項を含むモデルの場合，交互作用項も含みます），「自由度2」は分析モデルの残差の自由度です。

この結果の有意確率pの値が有意水準を下回る場合にモデルの適合度が有意と判断されますが，この検定結果が有意であっても，それは「切片のみのモデルよりはましである」という意味でしかない点には注意が必要です。

7.3.7 モデル係数

回帰分析の| モデル係数には次の項目が含まれています。ここでは，各予測変数の係数に関する設定を行います（図7.59）。

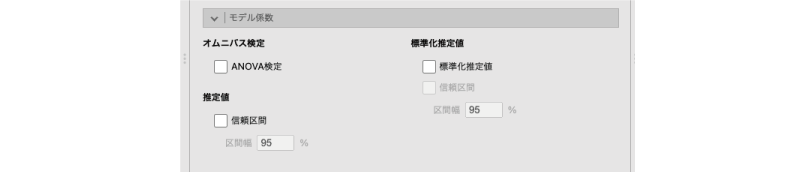
図7.59: モデル係数の設定

オムニバス検定　各予測変数についてオムニバス検定を行います。
- ANOVA検定　各予測変数の説明力が0でないかどうかを検定します。
推定値　回帰係数の推定に関する設定を行います。
- 信頼区間　回帰係数の信頼区間を算出します。
標準化推定値　回帰係数の標準化に関する設定を行います。
- 標準化推定値　標準化回帰係数を算出します。
- 信頼区間　標準化回帰係数の信頼区間を算出します。

オムニバス検定

「オムニバス検定」では，各予測変数の説明力が0でないかどうかについての検定を行うことができます。オムニバス検定というのは，分散分析のように「他と値の異なるものが少なくとも1つ含まれていることはわかっても，具体的にそれがどの値かまではわからない」タイプの検定のことです。

この「ANOVA検定」の部分にチェックを入れると，分析モデルから各予測変数を除外した場合とそうでない場合で，モデルの説明力に有意な差があるといえるかどうかについての検定結果が出力されます（図7.60）。

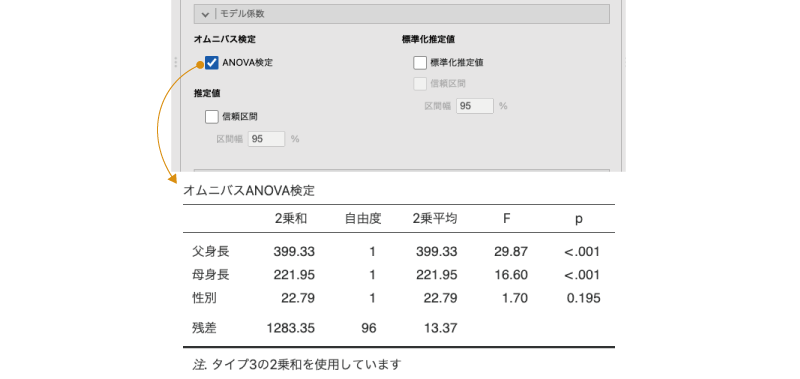
図7.60: オムニバス検定の結果

この検定の結果が有意でない予測変数は，従属変数の説明に貢献していないということですので分析から除外したほうがいいかもしれません。今回の分析では，「性別」の検定結果が有意ではありませんでした。

なお，回帰分析結果の「モデル係数」の表にも各係数についてのt検定の結果が出力されますが，これは「係数が0でない」，つまり影響力が0かどうかについての検定結果です。これに対し，このANOVA検定の結果は「その予測変数によって説明される分散が0でない」，つまりこの予測変数を用いる意味があるかどうかについての検定結果です。両者で検定仮説が異なる点に注意してください。

推定値

分析結果の表にもそう書かれているように，回帰分析で算出される回帰係数はあくまでも「推定値」であり，それが実際の関係を正確に示しているというわけではありません。そのため，回帰係数についても信頼区間を算出して検討することがあります。「推定値」にある「信頼区間」にチェックを入れると，回帰係数について指定した幅で信頼区間の上限と下限を算出することができます（図7.61）。

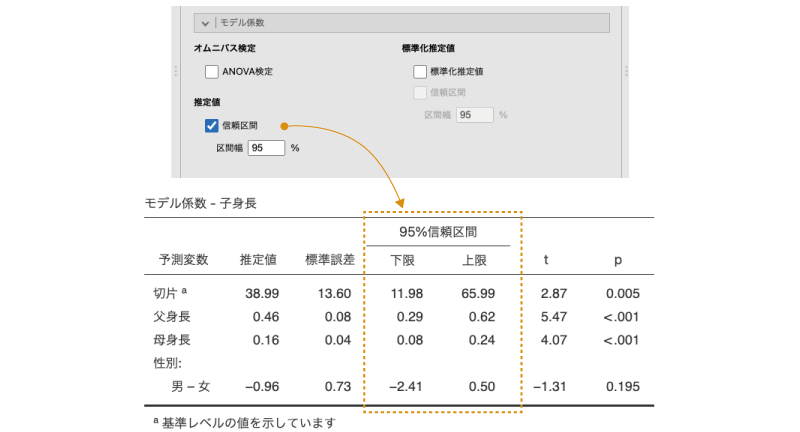
図7.61: 回帰係数の信頼区間

標準化推定値

重回帰分析における偏回帰係数の大きさは，予測変数の測定単位や大きさによる影響を受けます。たとえば，課題作業にかかった時間を分の単位で記録したもの（1.5分，0.75分など）を予測変数として用いた場合と，秒の単位で記録したもの（90秒，45秒など）を予測変数として用いた場合とでは，偏回帰係数の大きさが異なるのです。また，予測変数に「秒」を単位とする測定値と「mm」を単位とする測定値が含まれていた場合，それらの偏回帰係数の大きさを直接比較することはできません。1.2秒と0.7mmのどちらが大きいかというような判断はできないからです。

また，予測変数の単位がすべて同じである場合も，分散が大きな予測変数と小さな変数とでは，「1」のもつ意味合いが異なってきます。たとえば，長距離走のタイムにおける「1秒」の違いはごくわずかといえても50m走では「1秒」の差は非常に大きいといえるでしょう。これは，長距離走では分単位で測定値がばらつくのに対し，短距離走では測定値のばらつきの幅が数秒しかないためです。このように，測定値の分散の違いによって測定値における「1」の差の意味が大きく異なる場合もあります。

このような場合，偏回帰係数の大きさを見るだけでは，従属変数に対してどの予測変数がより強い影響を与えているのかを解釈することが困難です。そこでこのような場合には，各予測変数間の相対的な影響力を比較判断しやすくするために，それぞれの予測変数の値を標準化した場合の回帰係数を求めるという方法がとられます。このような，予測変数の値を標準化した場合の回帰係数のことを標準化回帰係数あるいは標準化偏回帰係数と呼びます。

jamoviで標準化回帰係数を算出する場合，| モデル係数の画面の右側にある「標準化推定値」のところにチェックを入れます。また，標準化回帰係数についても信頼区間を算出することができます。標準化回帰係数の信頼区間を算出するには，その下にある「信頼区間」にチェックを入れます（図7.62）。

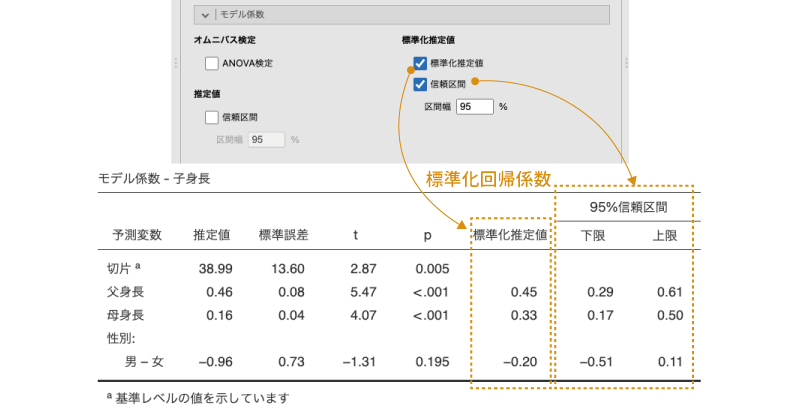
図7.62: 標準化回帰係数とその信頼区間

なお，各予測変数の値を標準化した場合，回帰式の切片の値はつねに0になります。そのため，jamoviでは切片の標準化推定値は空欄で表示されます。

7.3.8 推定周辺平均

| 推定周辺平均（推定周辺平均）の設定項目では，推定周辺平均値の算出や表示に関する設定を行います（図7.63）。

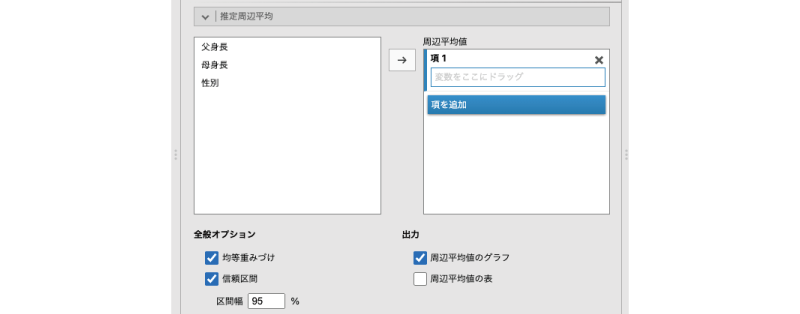
図7.63: 推定周辺平均

周辺平均値　周辺平均値の算出対象を指定します。
全般オプション
- 均等重みづけ
- 信頼区間　周辺平均値の信頼区間を算出します。
出力
- 周辺平均値のグラフ
- 周辺平均値の表

推定周辺平均値とは，回帰モデルに基づく予測値のことです。ここで簡単にその考え方を見ておくことにしましょう。たとえば次の回帰モデルを用い，子供の身長の推定周辺平均値を算出してみます。なお，「性別」は男児が「1」，女児が「2」と入力されているものとします。

\[ \text{子身長} = 38.03 + 0.48 \times \text{父身長} + 0.16 \times \text{母身長} + 0.96 \times \text{性別} \]

この場合，回帰式の「母身長」の値には，母親の身長の平均値（148.12）を代入します。また，「性別」の値はここでは「1」と「2」の中間である「1.5」を代入することにしましょう。すると，この回帰式は次のようになります。

\[\begin{eqnarray*} \text{子身長} & = & 38.03 + 0.48 \times \text{父身長} + 0.16 \times 148.12 + 0.96 \times 1.5 \\ & = & 38.03 + 0.48 \times \text{父身長} + 23.6992 + 1.44 \\ & = & 62.4792 + 0.48 \times \text{父身長} \end{eqnarray*}\]

すると，たとえば父親の身長が170cmであった場合，子供の身長は次のようになります。

\[\begin{eqnarray*} \text{子身長} & = & 62.4792 + 0.48 \times 170 \\ & = & 144.0792 \end{eqnarray*}\]

このような考え方で算出されたものが推定周辺平均値です。

この推定周辺平均の設定では，従属変数との関係を示す予測変数を「項」として指定します。このとき，「項」に指定されている変数が1つだけの場合にはその変数の主効果（その変数との単純な影響関係）について，複数ある場合にはそこに指定された変数間の交互作用についての推定周辺平均値が算出されます。

全般オプション

「全般オプション」では，推定周辺平均値の算出方法と，信頼区間についての設定が可能です。

均等重みづけ

先ほどの計算例では，「性別」の値は「1」と「2」の中間の値をとって「1.5」で計算しました。男女の人数が同じ場合，この変数の平均値は1.5になりますが，そうでない場合には1.5からは少しずれた値になります。この場合，単純に男女（1と2）の中間点の値（1.5）を用いるか，それとも男女の人数を考慮した中間点（平均値）を用いるかによって結果が異なってきますので，どちらを用いて計算を行うかについては「均等重みづけ」の部分で設定します。

ここにチェックが入っている場合は単純な中間点の値を用いた結果が，そうでない場合には両群の度数を考慮した中間点を用いて計算が行われます。なお，両群で度数が同じ場合や，名義尺度変数を予測変数に含まない場合には，このチェックのオン・オフは結果に影響しません。

信頼区間

「信頼区間」のチェックをオンにすると，推定周辺平均値を図示する際に，その信頼区間についても合わせて示すことができます。

出力

推定周辺平均値は，図または表，あるいはその両方で示すことができます。「出力」のところで「周辺平均値のグラフ」にチェックを入れればグラフが，「周辺平均値の表」にチェックを入れれば表が示されます（図7.64）。表の場合，その予測変数が平均値の場合と，平均値±1SDの場合のそれぞれの推定周辺平均値が表示されます。

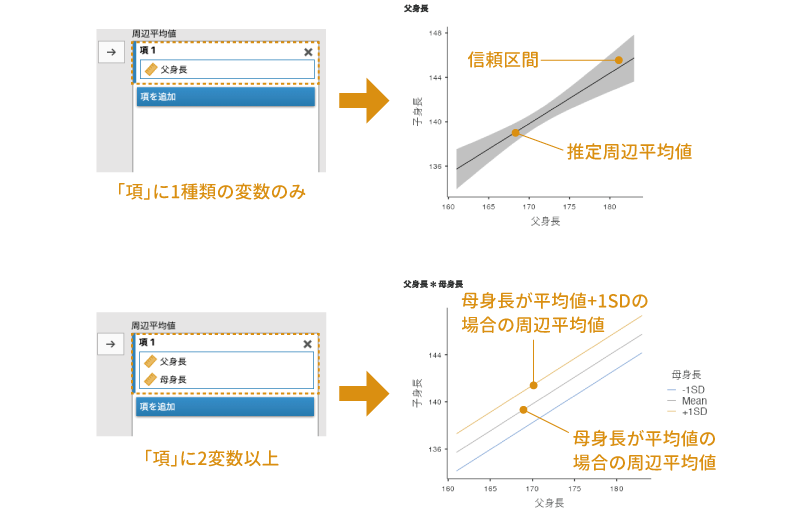
図7.64: 推定周辺平均のプロットの例

7.3.9 保存

分析で算出した各種の値を新たな変数として保存することもできます。回帰分析の「保存」には，次の項目が含まれています（図7.65）。

図7.65: 算出結果の保存

予測値　回帰モデルによる予測値を変数として保存します。
残差　回帰モデルの残差を変数として保存します。
クックの距離　クックの距離を変数として保存します。

このように，jamoviの「線形回帰」では，回帰モデルの予測値，残差，そして各測定値についてのクックの距離を新たな変数として保存することができます。変数として使用したい項目にチェックを入れて設定画面を閉じ，スプレッドシートを見てみると，データの一番最後の列にこれらの値が新たな変数として格納されているのがわかります。このようにして残差やクックの距離を新たな変数として保存することで，これらの値についてさらに詳しい分析を行ったり，これらの値を別の分析に用いたりすることができるようになります（図7.66）。

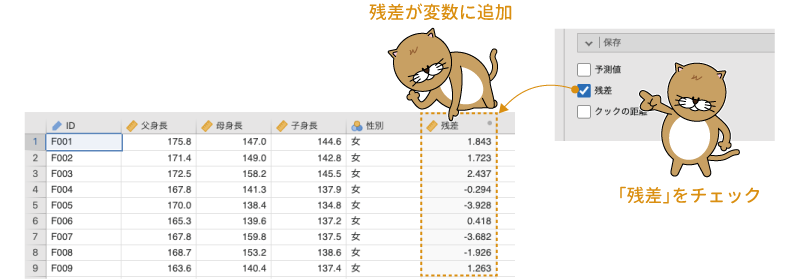
図7.66: 回帰分析の残差を保存した場合の例

なお，残念ながら，このようにして保存された変数（結果変数）に対してはフィルタ（第2章の2.5を参照）を適用することができません。フィルタによって表示されるデータ行が変わると，それによって分析結果も変化してしまい，そしてこれらの変数の値も変化してしまうからです。

そのため，たとえばクックの距離が5を超えるデータ行を特定したいというような場合には，データファイルを表計算ソフトなどに書き出して処理をするか，その変数の値を別のデータ変数に貼り付けてからデータフィルタを適用するといった工夫が必要になります。

Windows版のjamoviでは，変数名に日本語が含まれている際に正しく分析できません。以下の内容は，サンプルデータの変数名を英数字に変更したうえで実行してください。↩︎
複数の変数を同時に選択するには，いずれかの変数をクリックして選択したのち，「SHIFT(⇧)」キーを押しながらもう一方の変数名をクリックしてください。↩︎
3種類以上の値が含まれる名義型変数の場合には少し複雑になりますが，基本的な考え方はこれと同じです。↩︎
一定間隔ごとに測定された値など，時間的な順序が意味をもつデータのことです。↩︎
VIFの値が10以上の場合に問題があるとする考え方もあります。↩︎