8.5 対数線形回帰
カイ2乗適合度検定は1つの変数についての比率の分析,カイ2乗独立性検定は2つの変数を組み合わせた場合の比率の分析でした。では,3つ以上の場合はどうすればよいでしょうか。jamoviのカイ2乗独立性検定では,3つ目の変数値をグループ変数として層別分析を行うことも可能ですが,その場合,グループ変数と他の変数との関連については見ることができません。
このような,より複雑なデータの場合に使用可能な分析の1つに対数線形回帰分析があります。
8.5.1 考え方
話を単純にするために,ここでは表8.15のクロス集計表を例にこの分析の考え方について見てみましょう。これは,独立性検定のところで用いた性別とイヌ派・ネコ派のクロス集計表です。
| イヌ | ネコ | 計 | |
|---|---|---|---|
| 性別 | |||
| 男 | 70 | 30 | 100 |
| 女 | 55 | 45 | 100 |
| 計 | 125 | 75 | 200 |
このようなクロス集計表では,各セルの期待度数は,行の度数と列の度数,クロス集計表全体の総度数を用いて次のように求めることができます。
\[ \text{期待度数} = \frac{\text{行の度数}\times\text{列の度数}}{\text{総度数}} \]
たとえば,男性でイヌ派のセルの期待度数は,「(100×125)/200 = 62.5」となります。
このとき,この期待度数の式を対数変換すると,この式は次のように表すことができます4。
\[\begin{eqnarray*} \log(\text{期待度数}) % & = & \log\left(\frac{\text{行の度数}\times\text{列の度数}}{\text{総度数}}\right)\\ & = & \log(\text{行の度数})+\log(\text{列の度数}) - \log(\text{総度数}) \\ & = & - \log(\text{総度数}) + \log(\text{行の度数})+\log(\text{列の度数}) \end{eqnarray*}\]
各セルの期待度数について考えたとき,この式の「\(\log(\text{行の度数})\)」と「\(\log(\text{列の度数})\)」はセルごとに変化しますが,「\(-\log(\textsf{総度数})\)」の部分は,どのセルにおいても共通ですので,これは回帰式における切片のような役割を担っています。このように考えると,この式はさらに次のような回帰式として表せることになります。
\[ \log(\text{期待度数}) = b_0 + b_1\times \text{行の要素} + b_2\times \text{列の要素} \]
一般に,クロス集計表の検定では,行と列が独立であるかどうかについての検定を行いますが,これは行と列の組み合わせによって比率が異なるかどうかを検定しているのと同じです。先ほどの式には行の影響と列の影響しか含まれていませんが,ここに行と列の組み合わせの影響,つまり交互作用による影響を加えると,この式は次のようになります。
\[ \log(\text{期待度数}) = b_0 + b_1\times \text{行の要素} + b_2\times \text{列の要素} + b_3\times\text{行と列の交互作用} \]
対数線形回帰分析では,このように対数変換を用いて期待度数(の対数)を目的変数,行・列とその交互作用(の対数)を説明変数とする回帰式を作成し,そしてそれぞれの係数を算出するという形で複雑なクロス集計表についての分析を行います。
8.5.2 基本手順
ここでは,独立性検定の層別分析のところで用いたデータ(frequencies_data04.omv)で対数線形回帰分析の実施方法を見ていくことにしましょう。念のため,データファイルに含まれている変数の一覧を示しておきます。
性別性別(男,女)年齢年齢(大人,子供)ケーキケーキの種類- ショートケーキ:
ショート - チーズケーキ:
チーズ - チョコレートケーキ:
チョコ
- ショートケーキ:
人数そのケーキを選んだ人数
このデータを用いて,ケーキの選択に性別と年齢がどのように影響しているかをこれから分析していきます。
まず,分析タブの「 度数分析」から「対数線形回帰」を選択してください(図8.56)。
図8.56: 対数線形回帰分析の実行
すると,図8.57のような画面が表示されます。画面の構成は,回帰分析(第7章)のものとよく似ています。
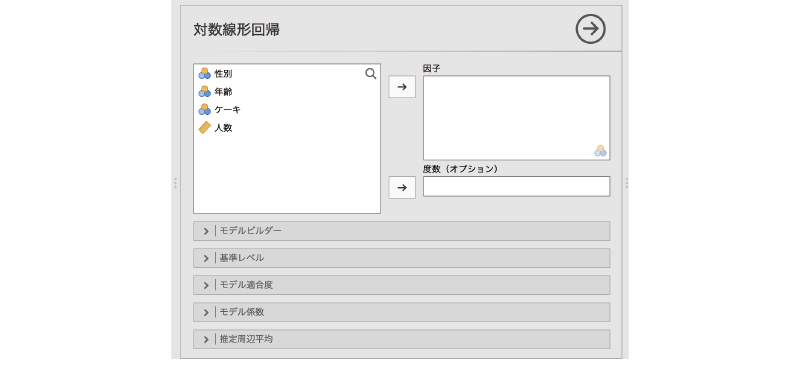
図8.57: 対数線形回帰分析の設定画面
- 因子 分析に使用する変数を指定します。
- 度数(オプション) 度数が入力されている変数を指定します(オプション)
- 交互作用を含むモデルの作成や複数モデルの比較を行います。
- 比較基準として用いる水準値を指定します。
- モデル適合度に関する設定を行います。
- モデル係数に関する設定を行います。
- 各主効果の周辺平均値(回帰モデルによる推定値)に関する設定を行います。
基本的な分析は,分析に使用する変数をすべて「因子」の部分に移動するだけです。また,今回のデータファイルのように度数集計済みのデータで分析する場合には,度数が入力されている変数(ここでは「人数」)を「度数(オプション)」の欄に指定します(図8.58)。
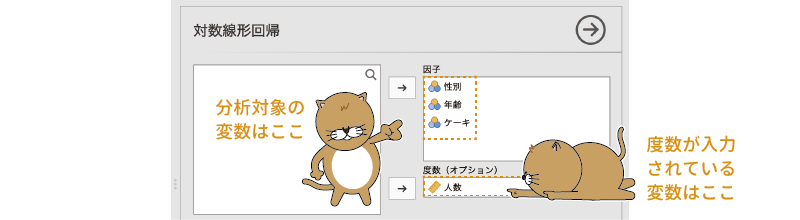
図8.58: 対数線形回帰分析の設定
実際にはもう少しいろいろと設定が必要なのですが,ひとまずこれで分析の基本設定はおしまいです。それでは結果を見てみましょう。
8.5.3 分析結果
対数線形モデルの結果は,図8.59のような形で表示されます。
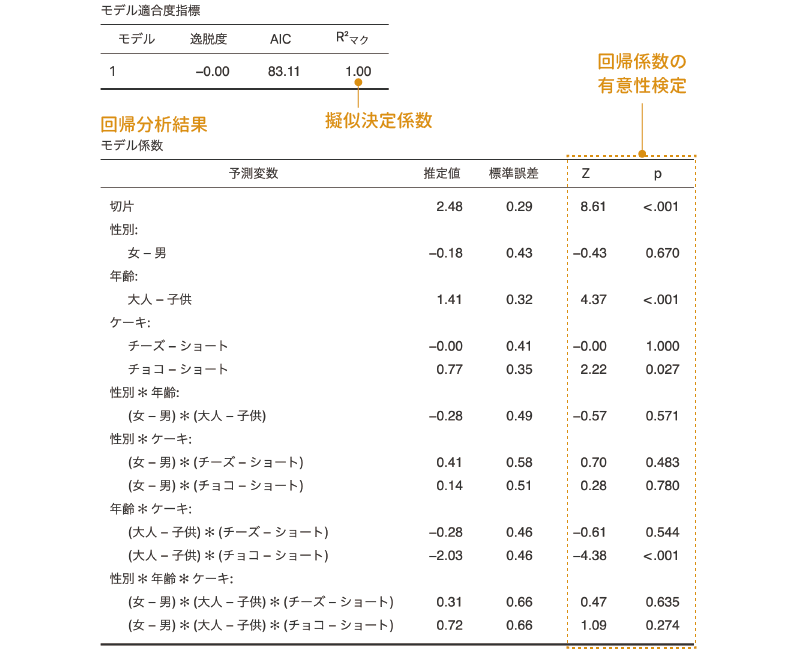
図8.59: 対数線形回帰分析の結果
分析の手順が簡単だった割に,随分と複雑な結果に見えます。この結果の表について,1つずつみていきましょう。
まず,結果の1つ目の表は,モデルの適合度に関する指標です。この表には,ロジスティック回帰分析の場合と同様に逸脱度とAIC,擬似決定係数が示されています。ただ,この分析結果では,じつはデータは完全に説明されていて,モデルとデータの残差はありません。このように実際の観測データを完全に説明したモデルは飽和モデルと呼ばれます。そのため,逸脱度は0になっており,マクファデンの擬似決定係数も1.00になっています。
そしてその下の表が回帰係数の推定値ですが,この表はとても複雑です。対数線形モデルでは,分析で説明変数として使用する変数はすべて名義型変数であるため,それらはすべてダミーコード化されています。そして,その変数値の1つを基準として比較した結果がここにまとめられているために,このように複雑な表になっているのです。
また,今回のデータにおける「ケーキ」のように,3つ以上のカテゴリーがある変数が含まれている場合,このダミーコード化の際にどの変数値を基準としたかによって,この表に示される係数やその係数が有意かどうかが大きく変化します。
そのため,実際にはこのままこの分析結果を解釈することはできません。データに含まれる関係の理解のためには,ここからもう少し分析モデルに修正を加えていく必要があります。
8.5.4 モデルビルダー
ここからは分析モデルの修正についてみていきましょう。この分析のモデルを修正するには,を使用します(図8.60)。
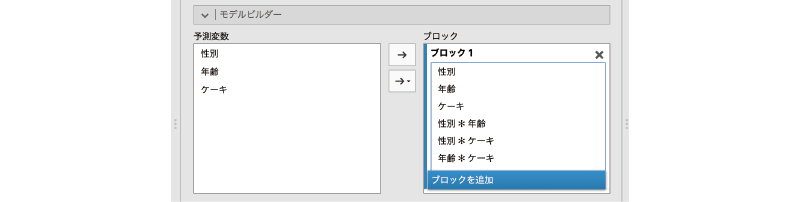
図8.60: モデルビルダー
分析の初期設定では,このモデルビルダーの「ブロック」には分析に使用する3つの変数(「性別」,「年齢」,「ケーキ」)の主効果と,これらの1次の交互作用,2次の交互作用のすべてが含まれています。これは先ほど結果の見方のところで説明したように「飽和モデル」と呼ばれるモデルで,このモデルでは観測データを完全に説明することが可能です。
飽和モデルはデータを完全に説明できる反面,構造が複雑になってしまうため,理解することが困難になりがちです。データ解析の目的は,そのデータに含まれる変数間の関係を解き明かし,理解することにあるわけですから,それでは困ります。そこで,この飽和モデルから結果に大きな影響を与えていない主効果や交互作用を取り除き,モデルを単純化していくことにします。
まずは,ブロックを追加をクリックして,新たなブロックを作成しましょう。そして,その新しく作成したブロックに,飽和モデルに含まれる項目のうち,もっとも複雑な項目である3変数の交互作用(2次の交互作用)「性別*年齢*ケーキ」を「ブロック1」から「ブロック2」にドラッグして移動します(図8.61)。
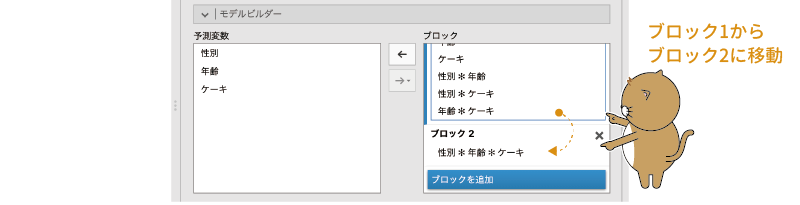
図8.61: 2次の交互作用をブロック2に移動
この状態で一度結果を見てみましょう。見る必要があるのは,「モデル適合度指標」と「モデルの比較」の部分です(図8.62)。
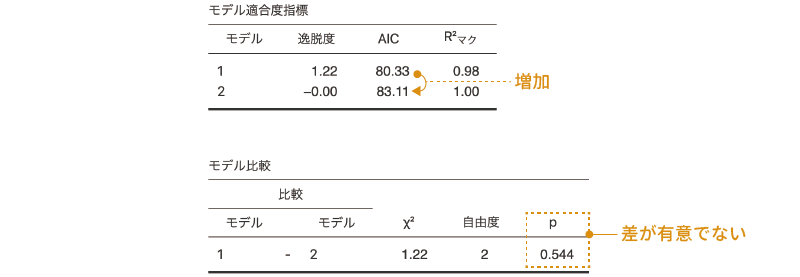
図8.62: モデルの比較
この結果を見てみると,すべての項目を含む飽和モデル(モデル2)と,そこから2次の交互作用を取り除いたモデル(モデル1)では,飽和モデルの方がAICの値が大きく,また,この2つのモデルで適合度に有意な差はないことがわかります。これはつまり,2次の交互作用はこのデータを説明するうえで余分というか過剰な項目であるということです。そこで,この交互作用は分析モデルから除外してしまいましょう。
モデルビルダーの「ブロック2」にある「性別*年齢*ケーキ」を選択し,「」をクリックして分析モデルから除外します(図8.63)。
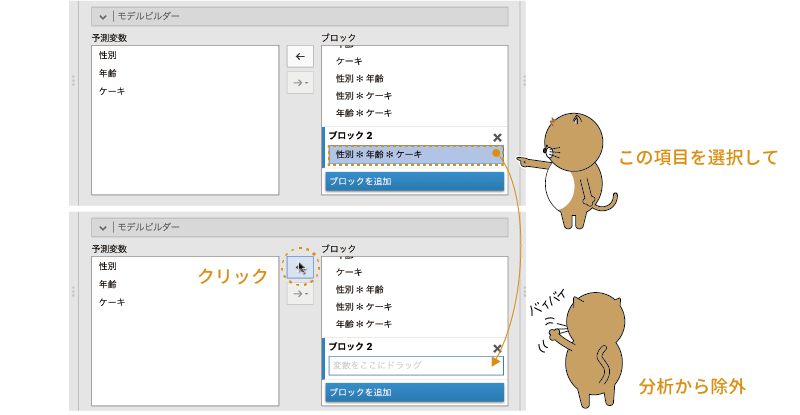
図8.63: 分析モデルから交互作用を除外
今度は1次の交互作用(2つの変数間の交互作用)についても見ていきましょう。1次の交互作用は,「性別*年齢」,「性別*ケーキ」,「年齢*ケーキ」の3つですが,このうち,「性別*ケーキ」と「年齢*ケーキ」の交互作用は,それぞれ「性別によってケーキの選択比率が違う」,「大人か子供かによってケーキの選択比率が違う」という意味ですが,「性別*年齢」の交互作用は「性別によって大人と子供の比率が違う」という意味で,これは今回の分析における関心とは関連がありません。また,今回のデータは大人も子供も男女同数ですので,この分析においては意味がない項目です。
そこで,今度はこの「性別*年齢」を「ブロック2」に入れて,これを除外した場合とそうでない場合とでモデルの適合度がどう変化するかを見てみましょう(図8.64)。
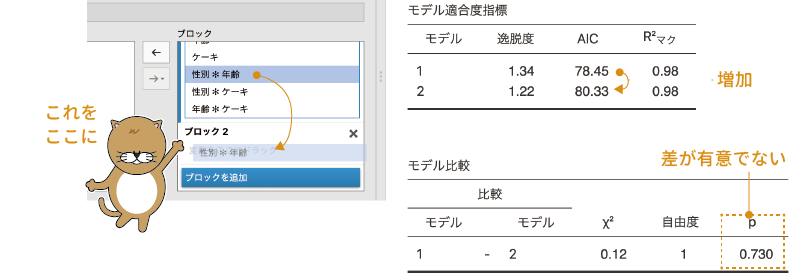
図8.64: 再度モデルを比較
すると,この場合も「性別*年齢」を除外したモデルの方がAICの値が小さく,相対的な適合度が高いことが示されました。また,2つのモデルで適合度に有意な差はありません。そこで,この交互作用もモデルから除外してしまいましょう。
1次の交互作用はあと2つ残っています。この2つはどちらも分析の関心と関連があるものですが,念のためモデルへの影響度を見ておきましょう。まずは「年齢*ケーキ」について,先ほどと同様にして結果を見てみましょう。すると,この場合の結果は図8.65のようになります。
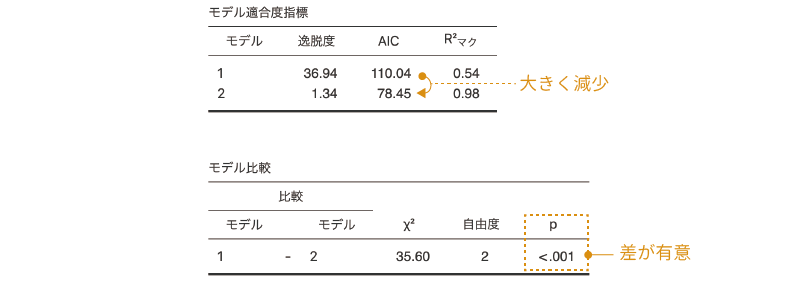
図8.65: 年齢とケーキの交互作用についての検討
この結果では,モデルに「年齢*ケーキ」の交互作用を加えることによって大きくAICの値が減少しており,また,これを入れたモデルと除外したモデルでは,適合度に有意な差があることがわかります。つまり,この交互作用はモデルから除外すべきではありません。
同様に,「性別*ケーキ」についても見てみましょう。この場合は図8.66の結果が得られます。
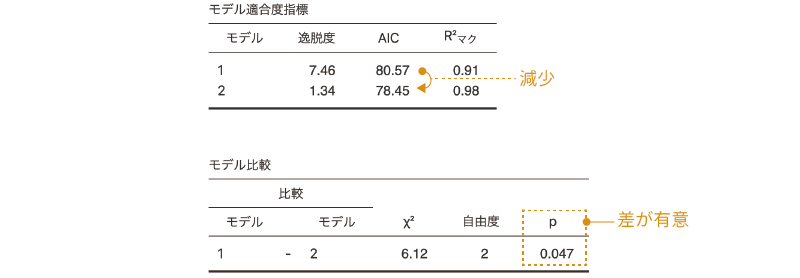
図8.66: 性別とケーキの交互作用についての検討
この結果から,「性別*ケーキ」の交互作用もモデルから除外しない方が良さそうです。
さて,次は「性別」,「年齢」,「ケーキ」それぞれの主効果についてですが,ここまでの結果では「性別*ケーキ」と「年齢*ケーキ」がモデルに含まれており,そしてこの3つの変数はこの交互作用の少なくとも1つに関係していますので,これらはモデルから除外することができません。そのため,ここでモデルの修正はおしまいということになります。
このようなモデル修正の結果,性別,年齢,ケーキの選択の各主効果と,性別×ケーキ,年齢×ケーキの交互作用から結果を説明できそうだということがわかりました。なお,ここでの分析の関心は,性別によって選択するケーキの比率に違いがあるか,年齢によって選択するケーキの比率に違いがあるかということでしょうから,これらのうち,とくに交互作用について中心的に見ていくことになります。
8.5.5 基準レベル
モデルの修正によって分析結果は単純化されたのですが,それでもまだ,「モデル係数」の結果の表の解釈には注意が必要です。基本設定のみの分析結果のところでも説明したように,この係数の値は,各変数のどの値を基準に考えるかによって大きく変わるからです。そのため,分析結果について検討するには,各変数における基準値をよく確認し,必要に応じて基準値を変更しなくてはなりません。
設定画面のを展開すると,初期状態では図8.67のようになっているはずです。
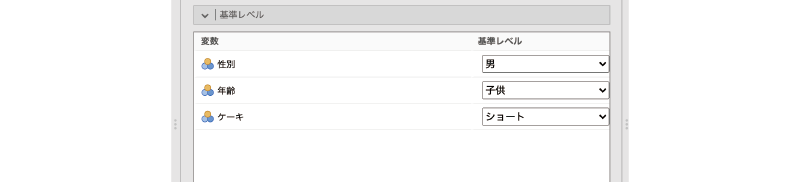
図8.67: 基準レベルの設定
そして,この状態での「モデル係数」の表は,図8.68のようになっています。
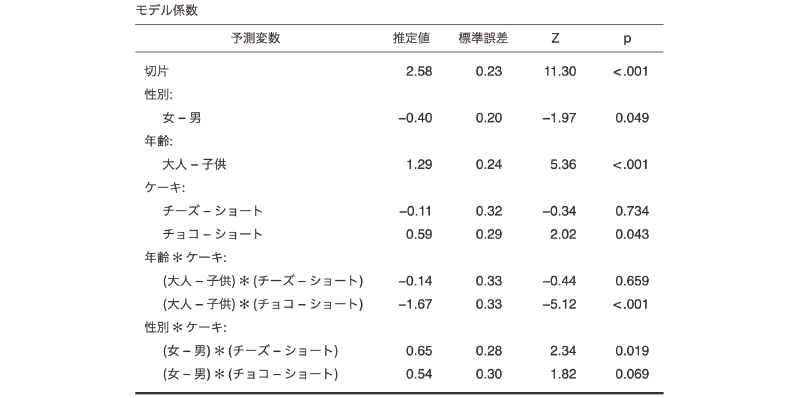
図8.68: 対数線形回帰分析の結果
この場合,結果の表では,「男」の「子供」で「ショート(ケーキ)」を選択した度数が入力されているセルが基準となっており,切片の値は,その基準セルについてこの分析モデルから推定される度数の対数値になっています。つまり,切片の値「2.58」を指数変換したもの(\(e^{\textsf{2.58}} = \textsf{13.2}\))が,「男性・子供・ショートケーキ」のセルの推定度数ということです。
そして,その下の「性別:」の部分には「女 - 男(男性と比較した場合の女性の値)」についての推定値があり,そしてこの値のpは0.049で有意になっていますが,これは,男性に比べて女性の度数が有意に小さいという意味ではなく,「男性・子供・ショートケーキ」のセルに比べて「女性・子供・ショートケーキ」のセルの度数が有意に小さいという意味です。この場合,「女性・子供・ショートケーキ」の推定度数は,切片の2.58に\(-\textsf{0.40}\)を加えた値を指数変換したもの(\(e^{\textsf{2.58}+(-\textsf{0.40})} = \textsf{8.85}\))になります。
同様に,その下の「年齢:」の部分にある「大人 - 子供」は,子供に比べて大人の度数が大きいということではなく,「男性・子供・ショートケーキ」のセルに比べて「男性・大人・ショートケーキ」の度数が有意に大きいという意味です。そしてこの係数から推定されるのは「男性・大人・ショートケーキ」の度数です。もし,「女・大人・ショートケーキ」の度数について推定したければ,そのセルは切片(男性・子供・ショートケーキ)から男性を女性に,子供を大人に変更した場合ということになるので,「女 - 男」の係数と「大人 - 子供」の係数の両方を切片に加えたもの(2.58 + (\(-\textsf{0.40}\)) + 1.29 = 3.47)を指数変換した値(\(e^{\textsf{3.47}} = \textsf{32.14}\))がその推定値ということになるのです。
その下の交互作用の部分はさらに複雑です。「性別*ケーキ:」の部分にある「(女 - 男)*(チーズ - ショート)」は,「大人・女性・チーズケーキ」のセルに関する推定値なのですが,この係数はあくまでも交互作用の影響のみについてのものであるため,このセルの推定値を算出したい場合には,切片の値に「女 - 男」の係数と「チーズ - ショート」の係数を加え,さらにそこにこの係数の値を加えたうえで指数変換する必要があります。
つまり,この結果の表に示されている主効果や交互作用の係数は,図8.69の関係について示したものなのです。
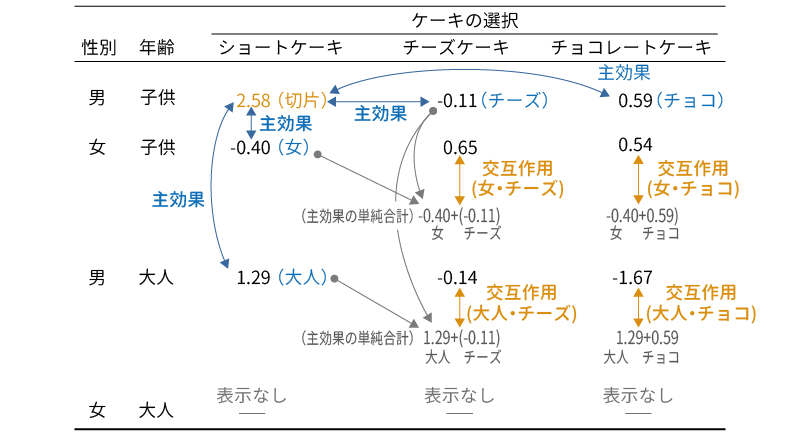
図8.69: 対数線形回帰分析の係数とクロス集計表の関係
そして,これらの結果からいえるのは次の点ということになります。ここでは,検定結果が有意であったもののみを示します。
- ショートケーキを選ぶのは,男児より女児の方が少ない(推定値 = \(-\textsf{0.40}\), p = 0.049)
- ショートケーキを選ぶのは,男児より男性の大人の方が多い(推定値 = 1.29, p < .001)
- 男児ではショートケーキを選ぶよりチョコレートケーキを選ぶ方が多い(推定値 = 0.59, p < .001)
- 女児でチーズケーキを選ぶのは,「女+子供+チーズケーキ」の組み合わせから想定される数よりも多い(推定値 = 0.65, p = 0.019)
- 大人の男性でチョコレートケーキを選ぶ人は,「男+大人+チョコレートケーキ」の組み合わせから想定される数よりも少ない(推定値 = \(-\textsf{1.67}\), p < .001)
このうち,「ショートケーキを選ぶ人では,大人の男性より男児の方が人数が少ない」の部分については注意が必要です。今回のデータファイルでは子供の人数は大人の半分であり,これはあたりまえの結果だからです。ですので,この部分に何か特別な意味があると勘違いしないようにしましょう。
また,ここに挙げた結果に検討したい部分が含まれていない場合には,で基準レベルを適切に変更し,そこで得られた結果を確認しなくてはなりません。
このように,対数線形回帰分析は結果の解釈が非常に複雑になってしまうのが難点です。
8.5.6 モデル適合度
設定画面のには,図8.70の項目が含まれています。

図8.70: 適合度指標の設定
- Fit Measures(適合度指標)
- 逸脱度 モデルの残差逸脱度を算出します。
- AIC 赤池情報量規準を算出します。
- BIC ベイズ情報量規準を算出します。
- モデル全体の検定 \(\chi^{2}\)を用いてモデル全体の有意性検定を行います。
- 擬似R² モデルのあてはまりの程度を標準化した値を算出します。
- マクファデンのR² マクファデンの擬似決定係数を算出します。
- コックス=スネルのR² コックス=スネルの擬似決定係数を算出します。
- ナゲルケルケのR² ナゲルケルケの擬似決定係数を算出します。
8.5.7 モデル係数
設定画面のには,次の項目が含まれています(図8.71)。
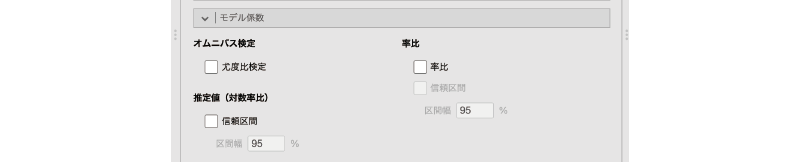
図8.71: モデル係数の設定
- オムニバス検定
- 尤度比検定 モデル全体の適合度について尤度比検定を行います。
- 推定値(対数率比)
- 信頼区間 対数率比の信頼区間を算出します。
- 率比
- 率比 率比を算出します。
- 信頼区間 率比の信頼区間を算出します。
尤度比を用いたオムニバス検定については,ロジスティック回帰の場合と同じですのでここでは説明を省略します。
それ以外の数値についても,基本はロジスティック回帰分析の場合と同じですが,ここで示されるのはオッズ比ではなく,各セルの比率に基づく率比(比率の比)である点には注意してください。対数線形モデルでは,回帰モデルの各係数は,対数オッズ比ではなく,比率の比の対数になっているからです。ただ,このように回帰係数の値の性質が少し異なるというだけで,表示される結果の見方や考え方はロジスティック回帰分析の場合と同じです。「推定値(対数率比)」の「信頼区間」にチェックを入れれば,回帰係数の信頼区間が算出されますし,「率比」の部分の設定を行えば,回帰係数を指数変換した値やその信頼区間を表示させることができます。
掛け算の式を対数変換した場合,その式は元の項目の対数同士の足し算として,割り算の式を対数変換した場合,その式は元の項目の対数同士の引き算として表すこができます。多変量解析の中でしばしば対数変換が行われるのは,このように掛け算を足し算に,割り算を引き算にできることで計算が単純になるということが理由の1つにあるのです。↩︎