2.7 演習：調査票データの処理

ここまで，jamoviにおけるデータ操作方法の基本についてひととおり見てきましたので，ここでは実際の分析場面により近い形で実践してみましょう。まず，練習用データファイル（basics_data01.omv）をjamoviで開いてください。

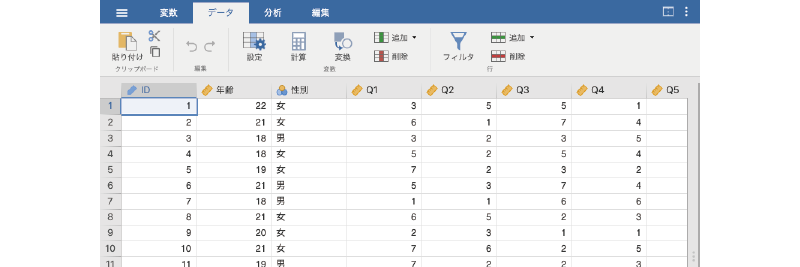
練習用データファイル

図2.32: 練習用データファイル

このデータファイルには，「ID」，「年齢」，「性別」の各変数値と，「Q1」から「Q7」までの回答値が入力されています（図2.32）。「Q1」から「Q7」は，それぞれ「外向性」を測定する心理尺度の回答データで，いずれも「まったくそう思わない（1）」から「とてもそう思う（7）」までの7段階で回答されています。「Q1」から「Q7」の質問内容は，変数タブで確認することができます（図2.33）4。

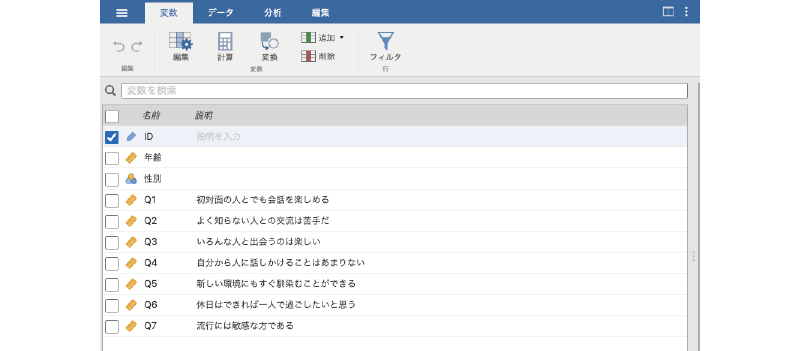
心理尺度の質問文

図2.33: 心理尺度の質問文

この練習データを用い，調査票データの分析場面でよく用いられる次の処理について実践してみましょう5。

  • 逆転項目の処理を行う
  • 尺度得点を算出する
  • 尺度得点に基づいて対象者をグループに分割する

2.7.1 逆転項目の処理

一般に，リカート法6などを用いた心理尺度では，1つの測定概念について複数の質問を用意して測定を行います。たとえば，「外向性」を測定したい場合には，「初対面の人とでも会話を楽しめる」や「いろんな人と出会うのは楽しい」といった，外向性の高さに関連する質問文を複数用意して，そのすべてに「まったくそう思わない（1）」から「とてもそう思う（7）」の7段階で回答させるということを行うわけです。

この際，それらの質問文の中には「よく知らない人との交流は苦手だ」のような，外向性の高さとは逆の内容の文が含まれていることがあります。このように，本来測定したいものとは逆の内容を含む質問文のことを逆転項目といいます（図2.34）。

逆転項目

図2.34: 逆転項目

この練習データでは，偶数番号の質問（Q2，Q4，Q6）が逆転項目になっています。この場合，「Q1」や「Q3」の質問に対して6や7と回答した人は外向性が高いことになるのですが，「Q2」や「Q4」に「6」や「7」と回答した人は外向性が低いことを意味します。このように，逆転項目は他の項目とは点数の方向が逆になるため，その扱いには注意が必要です。通常，こうした逆転項目の回答値は，それ以外の回答値と向きがそろうように変換したうえで分析に用います。

jamoviでは，逆転項目は「計算変数」または「変換変数」を用いて処理することができます。どちらを用いても構いませんが，逆転項目が複数ある場合には，変換変数を用いたほうが手軽に処理できるでしょう。そこで，ここでは変換変数を用いて逆転項目を処理することにします。

変換変数の作成

それでは，「Q2」について逆転項目の処理を行いましょう。ここでは，「Q2」のすぐ後ろに，回答値を逆転した変換変数「Q2.R」を作成します。

まず，「Q2」の列名のところをクリックして，「Q2」の列を選択します（図2.35）。

列の選択

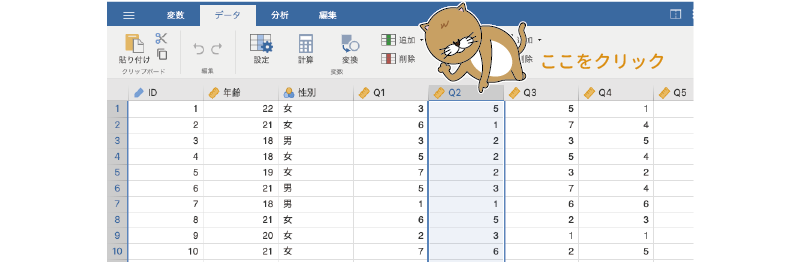
図2.35: 列の選択

その状態でデータタブの「変数」にある「inline 変換」ボタンをクリックします（図2.36）。

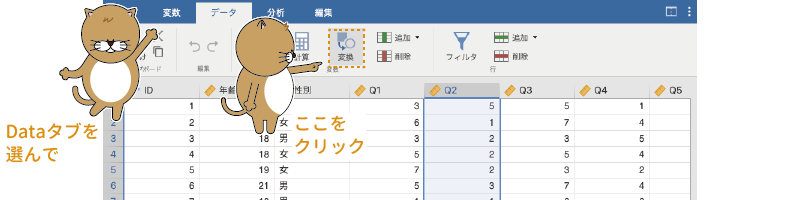
変換変数の追加

図2.36: 変換変数の追加

すると，図2.37のような変換変数の設定画面が表示されますので，作成した変換変数の名前を「Q2.R」に設定しましょう。このとき，「変換元の変数」の部分が「Q2」になっていることを確認してください。

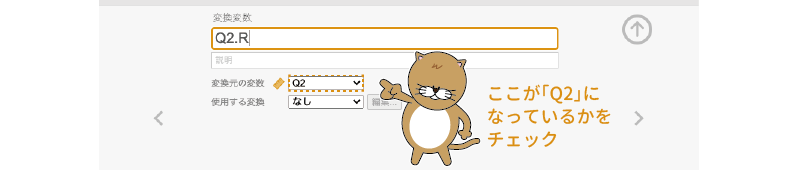
変換変数名の設定

図2.37: 変換変数名の設定

次に，「使用する変換」のメニューから「変換を新規作成…」を選択して実行します（図2.38）。

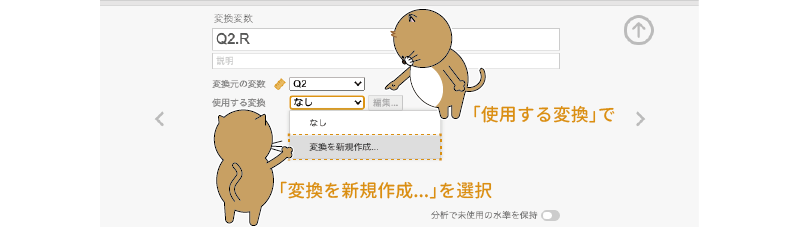
「変換」の作成

図2.38: 「変換」の作成

すると，図2.39のような「変換」の設定画面が表示されます。再利用の際にわかりやすいように，この変換の名前を「逆転項目」にしましょう。

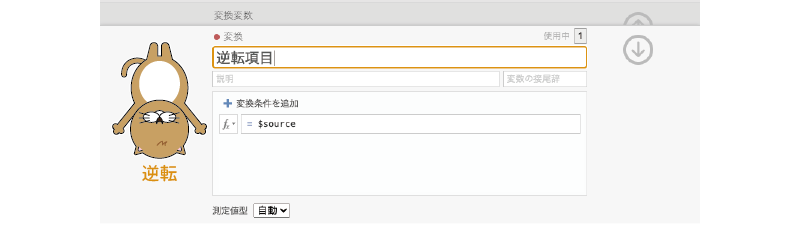
変換名の設定

図2.39: 変換名の設定

そして「変換条件を追加」の数式ボックスに逆転のための変換式を設定します。

5段階尺度や7段階尺度の場合，逆転項目の変換式は次の形で求めることができます。

\[ \text{逆転項目の回答値} = (\text{回答段階の最大値}+\text{回答段階の最小値}) - \text{元の回答値} \]

練習データでは，「Q2」は「1」から「7」までの値で回答してもらう形式ですので，逆転項目を処理する際の変換式は次のようになります。

\[ \text{逆転項目の回答値} = (7+1) - \text{元の回答値} = 8 - \text{元の回答値} \]

そこで，変換式の部分を次のように設定します（図2.40）。

= 8 - $source

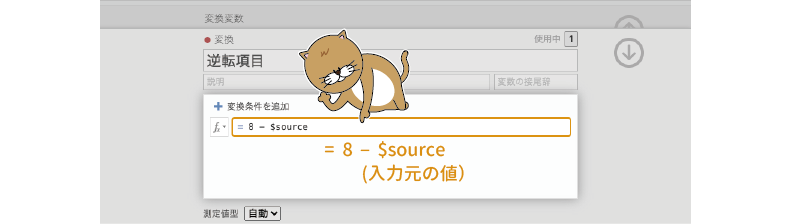
変換式の設定

図2.40: 変換式の設定

画面右側のinlineをクリックして変換の設定画面を閉じ，inlineで変数設定画面を閉じると，「Q2」のすぐ後ろの列に「Q2.R」という変換変数が作成されていることが確認できます （図2.41）。この変数が変換変数であることは，変数名の部分の右肩に小さな赤丸がついていることから判断できます。

この変数の値を確認すると，「Q2」の値が「1」の場合には「Q2.R」は「7」，「Q2」の値が「7」の場合には「Q2.R」は「1」というように，値が逆転しているのがわかると思います。

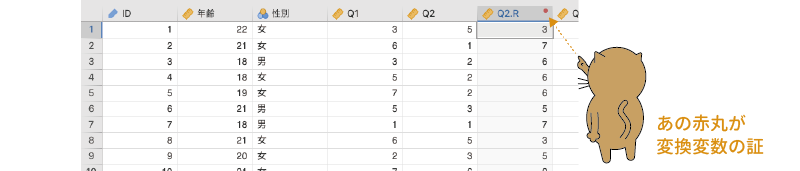
作成した変換変数とその目印

図2.41: 作成した変換変数とその目印

Q2の逆転処理はこれでおしまいです。次は「Q4」の逆転処理を行いましょう。「Q4」の列を選択して「inline 変換」をクリックすると，再び変換変数の設定画面が表示されます。新しく作成した変換変数の名前を「Q4.R」に設定したら，「変換元の変数」の部分が「Q4」になっていることを確認し，「使用する変換」のメニューをクリックしてください。すると，メニュー項目の中に，先ほど作成した「逆転項目」があるはずです （図2.42）。

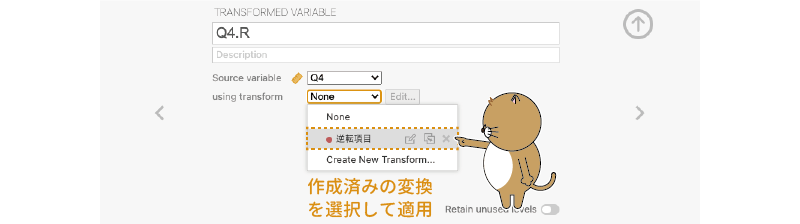
作成済みの変換を他の変数に適用

図2.42: 作成済みの変換を他の変数に適用

この「逆転項目」を選択して変数設定画面を閉じれば「Q4」の逆転処理は完了です。このように，一度作成した変換式は繰り返し利用できますので，逆転項目が複数ある場合には変換変数で逆転処理を行うのが便利です。

先ほどと同様の手順で，「Q6」についても逆転処理を行ってください。これで逆転項目の処理はおしまいです。

2.7.2 尺度得点の算出

「外向性」などの単一の概念について複数の質問文を用いて測定する場合には，それら複数の質問文に対する回答値を合計または平均し，それを尺度得点として用いるのが一般的です。ここでは，「Q1」から「Q7」までの回答の合計値を尺度得点として算出することにしましょう。なお，その際，「Q2」や「Q4」などの逆転項目については逆転処理を行った後の変数値（「Q2.R」や「Q4.R」など）を用いる必要がある点に注意してください。

この「外向性尺度」の尺度得点は，データの一番最後の列に新たな計算変数として作成しましょう。データタブの「変数」の欄にある「inline 追加」を使用して，新たな「計算変数」を「inline 追加」してください （図2.43）。

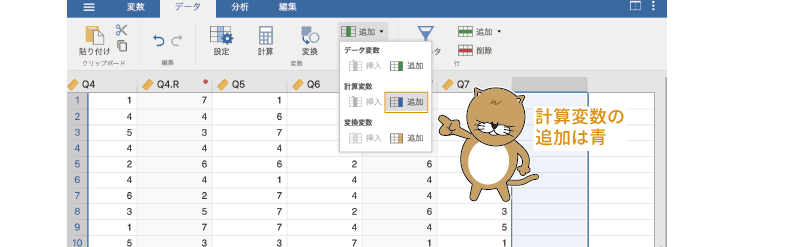
計算変数の追加

図2.43: 計算変数の追加

作成された計算変数の変数名部分をダブルクリックすると，変数の設定画面が表示されます。変数名は「N」になっているかと思いますが，このままだと何の値か分からないので，変数名を「外向性」に変更します （図2.44）。

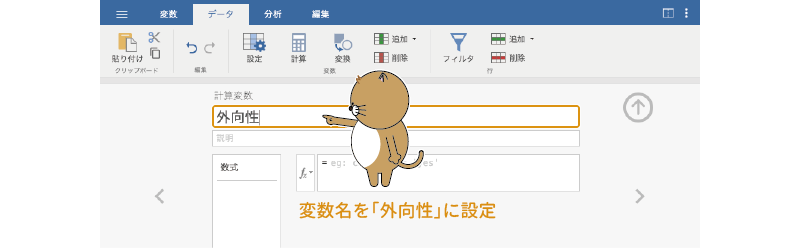
計算変数の名前を設定

図2.44: 計算変数の名前を設定

変数名の設定ができたら，その下の計算式の部分に，変数値を合計するための式を入力します。ここでは尺度得点として回答値の合計を用いるので，関数ボタン（inline）で表示される関数の中から「SUM」を探してダブルクリックします （図2.45）。この「SUM」という関数は，括弧の中に指定された値の合計値を求める関数です7。

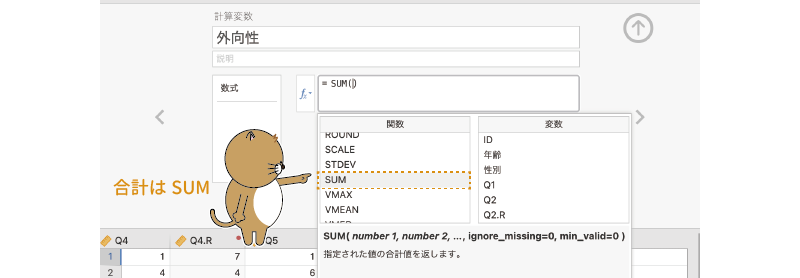
関数一覧からSUM関数を入力する

図2.45: 関数一覧からSUM関数を入力する

数式ボックスの中に「= SUM()」と入力されているのを確認したら，括弧の間に合計対象となる変数を記入していきます。この際，変数名はキーボードから入力してもよいですが，関数の右側に表示される変数一覧から必要な変数名をダブルクリックして入力したほうが，タイプミスの心配もなく，わかりやすいでしょう。今回，合計値の対象となるのは，「Q1」，「Q2.R」，「Q3」，「Q4.R」，「Q5」，「Q6.R」，「Q7」の7つの変数です。各変数の区切りにはコンマ（,）を使用します。変数名を1つ入力したらコンマ（,）を入力し，次の変数名を入力するようにしてください。また，コンマは必ず日本語入力をオフにした状態で入力してください。

完成した外向性得点の算出式は次のようになります （図2.46）。

= SUM(Q1, Q2.R, Q3, Q4.R, Q5, Q6.R, Q7)

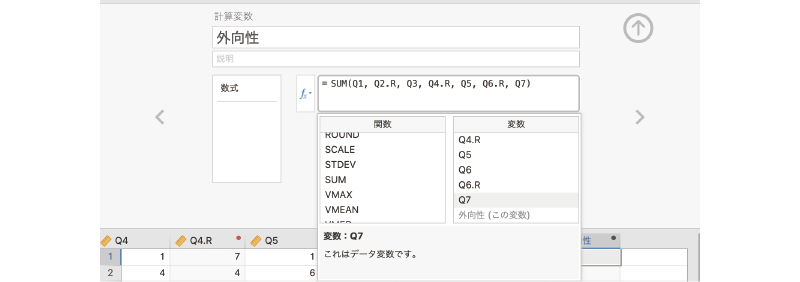
SUM関数を完成させる

図2.46: SUM関数を完成させる

式の入力が終わったら，画面右のinlineをクリックして変数設定画面を閉じます。これで各対象者の外向性得点（合計値）が算出されました （図2.47）。

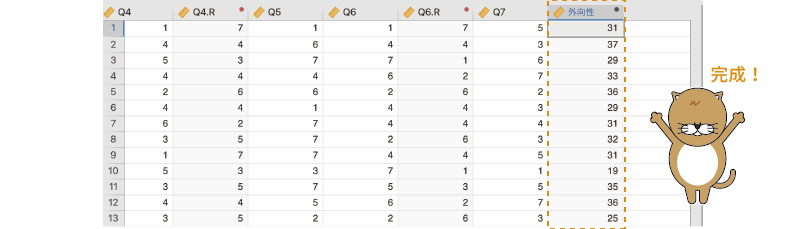
算出された外向性得点

図2.47: 算出された外向性得点

2.7.3 グループへの分割

実際の分析場面では，算出された尺度得点を元に，対象者を外向性が高い群と低い群に分けて分析するといったこともよく行われます。ここでは，外向性得点の平均値を基準に，平均値以上の人を外向性「高群」，平均値未満の人を外向性「低群」としてグループ分けする方法についてみていきます。

対象者を外向性の高・低2群に分割した結果は計算変数に格納しますので，「変数」の「inline 追加」から，新たな「計算変数」を「inline 追加」してください （図2.48）。

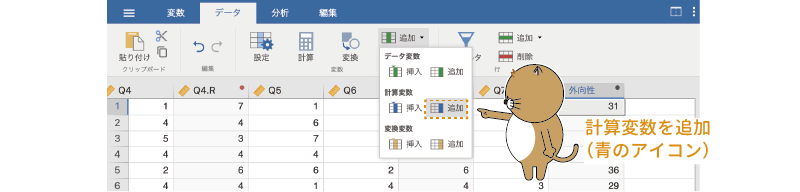
グループ分け用の計算変数を追加

図2.48: グループ分け用の計算変数を追加

そして新しく作成した計算変数の設定画面を開き，変数名を「群」に変更しましょう （図2.49）。

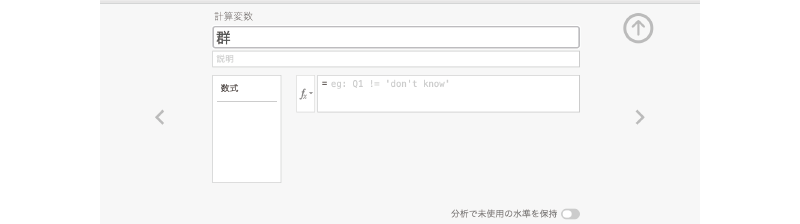
計算変数の名前を`群`に設定

図2.49: 計算変数の名前を群に設定

続いて，数式ボックスにグループ分けのための式を入力します。関数ボタン（inline）で表示される関数一覧の中から，「IF」を選択してください （図2.50）。このIF関数は，条件式の結果に応じて異なる値を設定できる関数です。

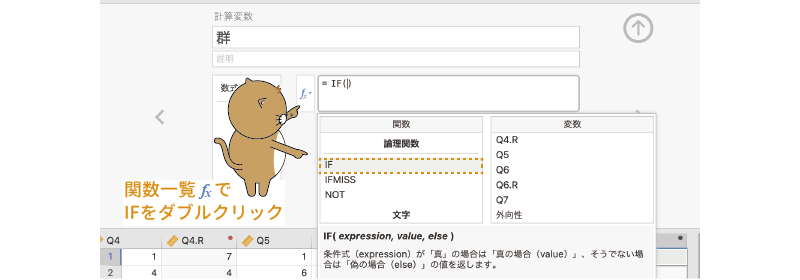
計算式でIF関数を使用

図2.50: 計算式でIF関数を使用

この「IF( )」の括弧の中には，次のように「条件式」，「条件式にあてはまる場合の値」，「条件式にあてはまらない場合の値」の3つをコンマで区切って指定します。

IF(条件式, あてはまる場合の値, あてはまらない場合の値)

今回は，外向性得点の平均値を基準にして対象者を外向性高群と低群の2群に分割したいので，「条件式」の部分には各対象者の外向性得点が平均値以上であるかどうかを判断する式（\(\text{外向性得点} \geqq \text{外向性得点の平均値}\)）を記入することになります。

そこでまず，変数名一覧から「外向性」をダブルクリックして括弧内に入力し，続けてキーボードから>=と入力します （図2.51）。

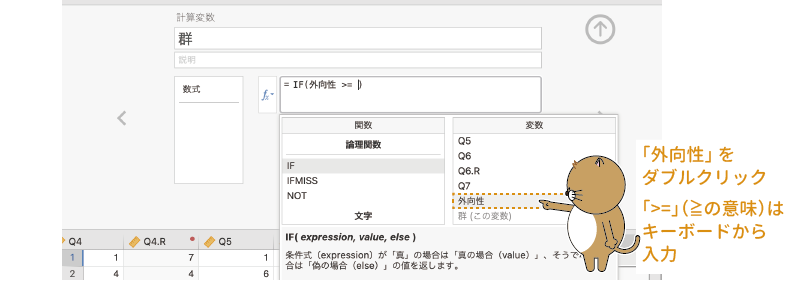
条件式の入力

図2.51: 条件式の入力

さらに，関数一覧から「VMEAN」を選択して入力します （図2.52）。この「VMEAN」は，指定した変数の平均値を算出する関数です8。

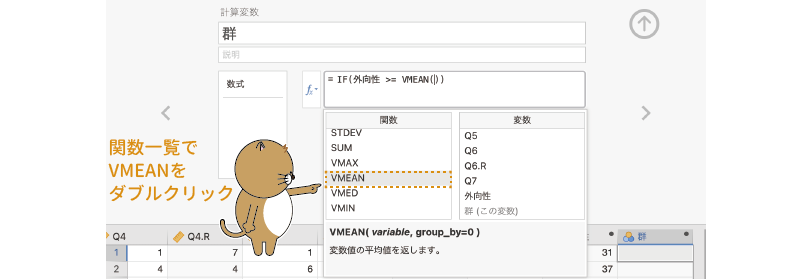
全体の平均値の算出式を入力

図2.52: 全体の平均値の算出式を入力

そしてこの「VMEAN」関数の括弧の中に「外向性」を指定します （図2.53）。

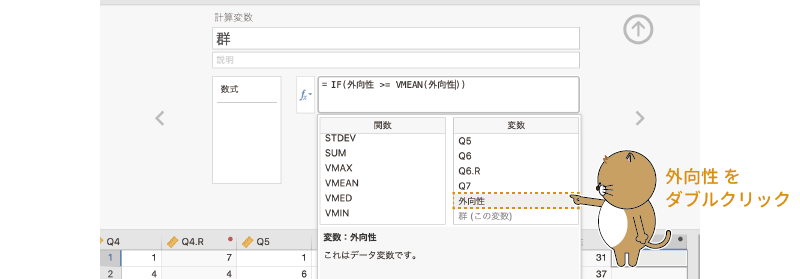
平均値を算出する変数を指定

図2.53: 平均値を算出する変数を指定

この「外向性 >= VMEAN(外向性)」の式が，「\(\text{外向性得点} \geqq \text{外向性得点の平均値}\)」を意味します。この条件式に続けて，条件式にあてはまる場合の値として「高群」，あてはまらない場合の値として「低群」を，それぞれコンマ（,）で区切って入力します （図2.54）。このとき，変数値に「高群」や「低群」のような文字を用いる場合には，その値を引用符（""）で括る必要がありますので注意してください。


=IF(外向性 >= VMEAN(外向性), "高群", "低群")
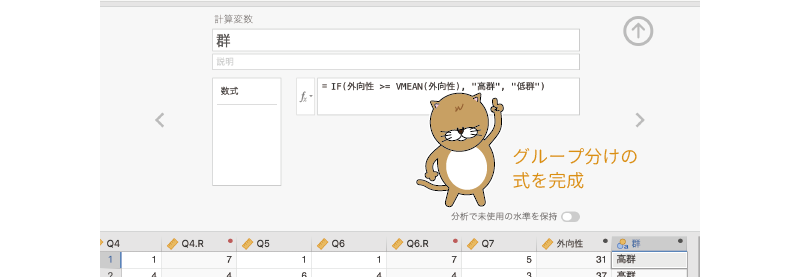
グループ分けの式を完成させる

図2.54: グループ分けの式を完成させる

式を完成させて変数設定画面を閉じると，新しく作成した「群」変数に「高群」または「低群」が値として入力されているのを確認することができます （図2.55）。条件式の部分がやや難しく感じられたかもしれませんが，計算変数ではこのようにしてデータをグループ分けすることもできるのです。

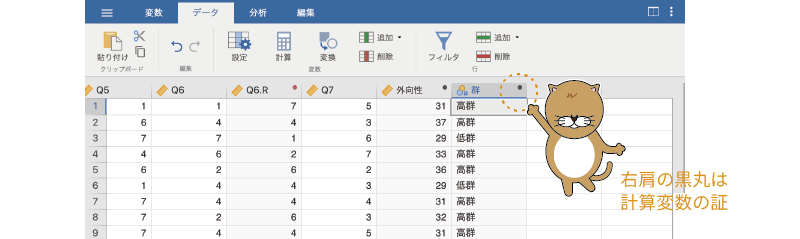
グループ分けの変数の完成

図2.55: グループ分けの変数の完成

このような，逆転項目の回答値の処理や尺度得点の算出，グループ分けといった処理は，Excelなどの表計算ソフトで行うこともできますし，そのほうが簡単だと思う人もいるかもしれません。しかし，表計算ソフトで処理をした場合，元のデータに入力ミスが見つかったなどの理由でデータに修正が生じた際には，これらの処理をやり直さなければなりません。

これに対し，jamoviでこれらの処理を行った場合には，仮に元のデータに修正が生じたとしても，計算変数や変換変数の値は自動的に最新の内容に更新されるため，計算し直す必要がありません。分析データを確実に最新の状態に保てることは，jamoviでデータ処理を行う大きな利点といえます。

  1. この尺度は，この練習用に作成した架空のものです。↩︎

  2. ここでとりあげる3つの処理のうち，最初の2つについてはjamoviの分析ツールを使用して行うこともできます。↩︎

  3. 各質問文に対し「あてはまらない」，「どちらでもない」，「あてはまる」など，複数の段階で回答させて数量化する方法↩︎

  4. 尺度得点に平均値を用いる場合には，「MEAN」関数を使用します。これらの関数の詳細については付録の関数一覧を参照してください。↩︎

  5. 平均値を算出する関数には「MEAN」と「VMEAN」の2つがありますが，「MEAN」は複数の変数値の平均値を「各対象者ごと」に計算するのに対し，「VMEAN」は1つの変数値について「対象者全体」での平均値を算出する点が異なります。↩︎