6.1 1要因分散分析
分散分析にはさまざまなタイプのものがあるのですが,その中でもっとも単純なものが1要因分散分析です。1要因分散分析の「要因」とは,平均値に影響を与えると考えられる要素のことです。
たとえば,ある性格特性について男女で平均値に差があるかどうかを検討したいとします。その場合には,対象者の「性別」が「要因」に相当します。同様にして,ある技能について幼稚園児と小学校低学年,中学年の児童の間で比較したい場合には,対象児の「年齢(学年)」が「要因」ということになります。
1要因分散分析とは,このような要因を1種類だけ用いた分散分析のことです。分析に2つの要因(たとえば性別と学年)を用いる場合には,2要因分散分析,3つの要因(性別と学年,地域など)を用いるなら3要因分散分析です。要因の数が1つであっても複数であっても基本的には同じように分析が可能なのですが,jamoviでは1要因分散分析については個別に分析メニューが用意されていますので,まずはこの1要因分散分析のメニューを用い,分散分析の基本について見ていくことにします。
6.1.1 考え方
ここでは,次のサンプルデータ(anova_data01.omv)を用いて分散分析の基本的な考え方について見ていくことにしましょう(図6.2)。
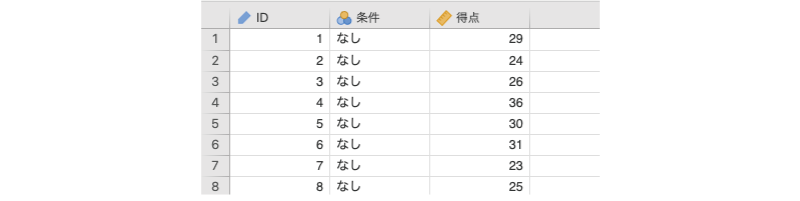
図6.2: サンプルデータ
ID実験参加者のID条件文字条件(なし,不一致,一致)得点課題の成績(0〜50点)
このデータファイルには,ある実験における認知課題の成績が記録されています。この実験では,イヌとネコの写真を1枚ずつ左右に並べてPC画面に表示し,そのうちの「ネコ」の写真が呈示されたほうのボタンをできるだけ素早く押してもらうという課題を行いました。その際,実験条件として,ネコの写真の下に「ネコ」,イヌの写真の下に「イヌ」と表示する条件(一致条件),ネコの写真の下に「イヌ」,イヌの写真の下に「ネコ」と表示する条件(不一致条件),文字は表示せず,写真だけを呈示する条件(文字なし条件)の3条件で測定を行っています。
この実験では,3つの測定条件それぞれについて25名,合計75名の参加者からデータを収集しました。データファイルの「条件」は実験条件,「得点」はこの課題成績を0点から50点の範囲になるように得点化した値です。ここでは,実験条件によって成績の平均値に差が見られるかどうかについて確かめたいとします。
まず手始めに,実験条件ごとの平均値と標準偏差を算出してみましょう。分析タブの「 探索」から「記述統計」を選択して実行し,「変数」欄に「得点」を,「グループ変数」に「文字」を指定してください(図6.3)。
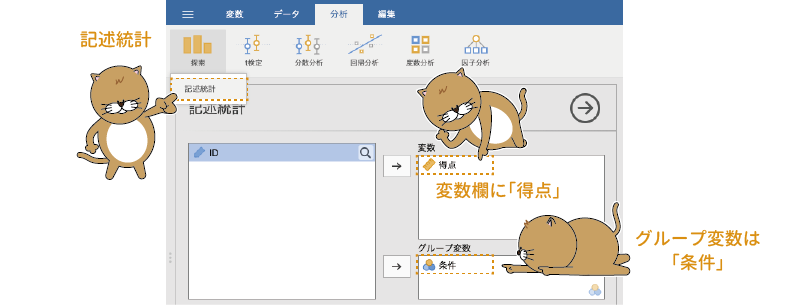
図6.3: まずは記述統計から
変数一覧のすぐ下にある「記述統計」の部分を「行に変数を配置」にし,設定画面ので平均値と標準偏差のみチェックして結果を表示させると図6.4のような結果が得られます。

図6.4: 各条件の平均値と標準偏差
この結果を,標準偏差を誤差線としてグラフに示すと図6.5のようになります。このグラフはjamoviではなく別のソフトウェアで作成したものですが,このようにしてグラフに示すと,各測定条件の間で平均値にばらつきがありそうだということだけでなく,それぞれの条件においても測定値にばらつきがあることがわかります。
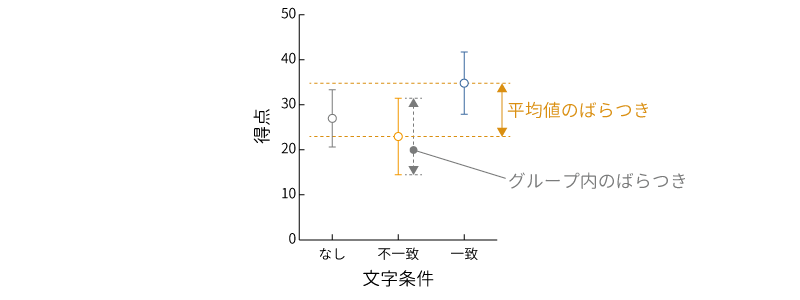
図6.5: 各条件の平均値と標準偏差のグラフ
この,それぞれのグループ内での測定値のばらつきは,同じ実験条件内におけるばらつきなわけですから,実験条件の違いからは説明できません。これらは,実験条件とは別の要因(個人差や測定誤差など)によって生じている一種の誤差と考えられます。
ここで,もし実験条件の違いによる平均値のばらつきがグループ内の測定値のばらつきよりも小さかったとすると,実験条件による平均値の差は誤差と変わらない,つまり大した違いではなということになります。そうでなく,実験条件による平均値の差が誤差と考えられるグループ内のばらつきよりも十分大きな場合には,実験条件によって平均値が大きくばらついている,つまり実験条件の違いによって平均値に差があると考えられるわけです。
このように,分散分析はじつは平均値そのものについて検定しているわけではありません。条件間での平均値のばらつきが,グループ内での測定値のばらつき(誤差)より大きいといえるかどうかを検定しているのです。この分析が「分散分析」と呼ばれるのは,このようにして平均値や誤差のばらつき(分散)を用いて分析を行うためです。
なお,t検定の場合と同様に,分散分析にも対応なしの場合と対応ありの場合とがありますが,ここではまず,対応なしのデータを用いた分散分析について見ていくことにします。
6.1.2 分析手順
それでは分析手順を見てみましょう。分析の実行には,分析タブの「 分散分析」から「1要因分散分析」を選択します(図6.6)。
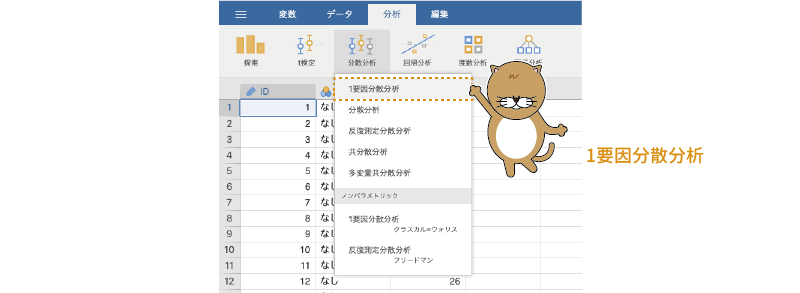
図6.6: 1要因分散分析の実行
1要因分散分析の設定画面は次のようになっています(図6.7)。詳細については,後ほど個別に見ていくとして,ここではまず,大きな部分の構成だけを見ておきましょう。
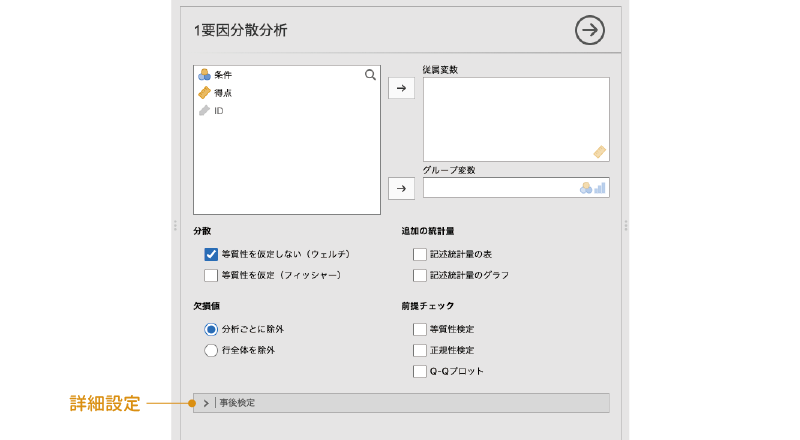
図6.7: 1要因分散分析の設定画面
- 従属変数 分析対象の測定値が入力されている変数を指定します。
- グループ変数 グループの値が入力されている変数を指定します。
- 分散 分析における分散の扱い方について設定します。
- 欠損値 欠損値の処理方法について設定します。
- 追加の統計量 記述統計量の算出と表示に関する設定を行います。
- 前提チェック 分散分析の前提が満たされているかどうかを確かめます。
- 分散分析の事後検定に関する設定を行います。
1要因分散分析の基本設定は,対応なしt検定の場合とよく似ています。分析対象の測定値が入った変数を「従属変数」の欄に,グループの別が入力されている変数を「グループ変数」の欄に移動すれば,基本的な分析は終了です(図6.8)。
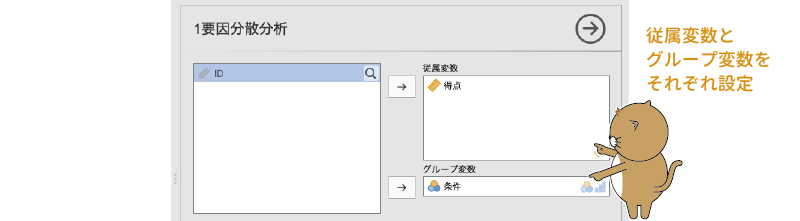
図6.8: 1要因分散分析の分析設定
すると,図6.9のような形で分析結果が表示されます。

図6.9: 1要因分散分析の結果
分散分析では,F分布と呼ばれる確率分布を利用して検定を行います。このFは,2つの分散の比に関する分布です。分散分析では,各条件の平均値の差(これを主効果といいます)の分散が誤差の分散の何倍の大きさかという形で検定統計量Fを算出します。そのため,主効果の分散の自由度(自由度1)と誤差の分散の自由度(自由度2)という,2種類の自由度が結果に表示されます。
表の右端の「p」は,このFの値についての有意確率です。このpの値が有意水準よりも小さければ条件間の平均値の分散が誤差の分散よりも有意に大きい(条件間で平均値に差がある)とみなします。
この分析結果では,有意確率は「p<.001」ですので,検定結果は有意です。つまり,実験条件によって課題成績の平均値に差があるというのが分析結果です。
6.1.3 分析の詳細設定
対応なしt検定の場合と同様に,1要因分散分析も基本的な分析方法は非常に簡単なのですが,適切な結果を得るためには,この分析においてどのような設定が可能であるのかを知っておく必要があるでしょう。ここでは,1要因分散分析における分析設定の詳細について見ておくことにします。
分散
分析設定画面の「分散」には,次の2つの項目が含まれています。
- 等質性を仮定しない(ウェルチ) 各グループの分散が等しいと想定しない形で分析を行います(ウェルチの検定)
- 等質性を仮定(フィッシャー) 各グループで分散が等しいという仮定の元に分析を行います(フィッシャーの検定)
この設定項目は,分析において各条件の分散をどう扱うかについての設定です。
対応なしt検定でも,2群で分散が等しいという仮定をおくか(スチューデントの検定),そのような仮定をおかないか(ウェルチの検定)という選択肢がありましたが,これは分散分析においても同様です。分散分析はイギリスの統計学者フィッシャーによって開発された手法ですが,この方法は各条件で分散が等しいことを前提としています。一般的な心理統計法の教科書で説明される分散分析はこちらの方法です。これに対し,ウェルチによる修正法ではそのような前提は必要としません。jamoviの1要因分散分析では,この2つの方法のどちらを用いるかを選択することができます。
等質性を仮定しない(ウェルチ)
この設定項目で「等質性を仮定しない(ウェルチ)」にチェックを入れると,各条件で分散が等しいという前提をおかない形で分析を行った結果が表示されます。jamoviの分散分析では初期設定値ではこちらの方法が選択されていますので,先ほど見た結果の表にも「1要因分散分析(ウェルチ法)」というように,ウェルチの方法を用いて分析したことが示されていました。
等質性を仮定(フィッシャー)
もう一方の「等質性を仮定(フィッシャー)」にチェックが入っている場合は,各条件の分散が等しいという前提のもとで分散分析を行った結果が表示されます。
この2つの方法で分析結果を比較して見てみると,検定統計量Fの値や誤差の自由度の値がかなり異なっているのがわかります(図6.10)。

図6.10: 1要因分散分析の結果
適切な分析結果を得るためには,この2つの方法のどちらを用いるべきかをしっかり見極めなくてはなりません。
欠損値
設定画面の「欠損値」には,次の2つの項目が含まれています。
- 分析ごとに除外
- 行全体を除外
これらはいずれも対応なしt検定のところで説明したものと同じですので,ここでは説明を省略します。詳細については対応なしt検定(第5章)の「欠損値」のところを参照してください。
追加の統計量
この「追加の統計量」では,各条件の記述統計量を表に示すか,グラフに示すかを設定できます。
- 記述統計量の表
- 記述統計量のグラフ
ここで「記述統計量の表」にチェックを入れると記述統計量が表に,「記述統計量のグラフ」にチェックを入れると記述統計量が図に示されます(図6.11)。
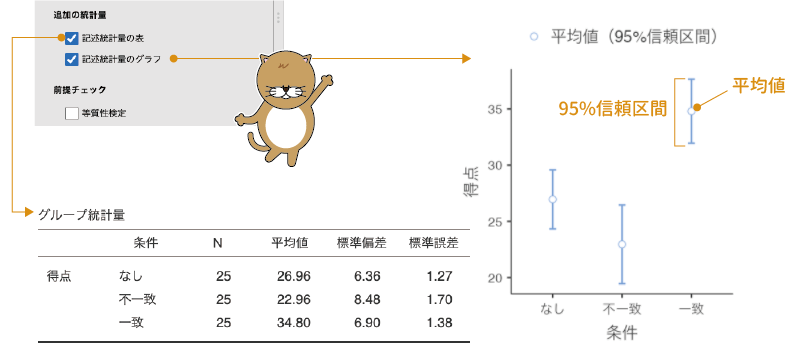
図6.11: 追加の統計量の設定
この設定で作成される記述統計量の表には,各条件の標本サイズ,平均値,標準偏差と平均値の標準誤差が示されます。また,記述統計量の図には,各条件の平均値と95%信頼区間が示されます。
前提チェック
設定画面の「前提チェック」には,次の3つの項目が含まれています。
- 等質性検定 分散の等質性についての検定を行います。
- 正規性検定 データの正規性についての検定を行います。
- Q-Qプロット 正規Q-Qプロットを作成します。
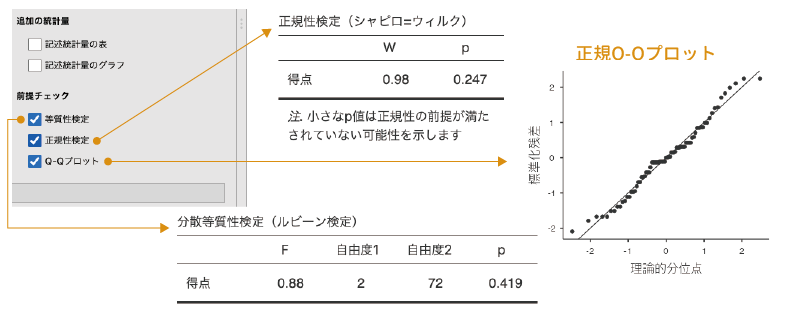
図6.12: 前提チェック
等質性検定
先ほど「分散」の設定のところでも触れたように,フィッシャーの方法による分散分析では,各条件で分散が等しいことが前提条件の1つとなっています。そこで「等質性検定」では,ルビーン検定を用いて分散の等質性についての検定を行います。この検定では,「分散が等しい」ことを帰無仮説としているので,p値が有意水準を下回る場合には,分散が有意に異なるという結論になります(図6.12)。分散が有意に異なる場合には,フィッシャーの方法による分散分析では適切な結果が得られない可能性が高くなります。
6.1.4 事後検定
分散分析では,条件の違いによって生じる平均値のばらつきが誤差による測定値のばらつきよりも大きいかどうかを検定しています。そのため,分散分析の結果が有意であった場合,条件によって平均値が異なる場合があるということはわかっても,どの条件とどの条件の間に差があるのかまではわかりません。
そこで,分散分析の結果が有意であった場合には,どの条件間に差があるのかを確かめるために多重比較と呼ばれる方法がとられるのが一般的です。多重比較では,3つあるいはそれ以上の条件の中から2つずつのペアを形成し,それぞれのペアについてt検定を行うという形で分析が行われます。ただし,そのままt検定を繰り返すと,検定全体での有意水準が設定した値(一般にはα=0.05)を大きく超えてしまうため,そうならないように調整を行った方法で比較が行われます。このようにして,分散分析の実施後に行われる詳細についての分析は,事後検定とも呼ばれます。
1要因分散分析のには,次の設定項目が含まれています。
- 事後検定 事後検定についての設定を行います。
- なし 事後検定を行いません。
- ゲームス=ハウエル(非等分散) ゲームス=ハウエル法による多重比較を行います。この方法では分散の等質性を仮定しません。
- テューキー(等分散) テューキー法による多重比較を行います。この方法では各条件の分散が等質であることが前提となります。
- 統計量 事後検定の統計量に関する設定を行います。
- 平均値の差 条件間の平均値の差を算出します。
- 有意性を報告 検定統計量の有意確率(p値)を表示します。
- 検定結果(tと自由度) 検定統計量と自由度を表示します。
- 差が有意なペアに印 差が有意であったペアに「*」などの印をつけて示します。
事後検定
まず,事後検定の方法について見てみましょう。jamoviの1要因分散分析では,多重比較の方法としてゲームス=ハウエル法と呼ばれる手法とテューキー法と呼ばれる手法の2とおりを使用することができます。
ゲームス=ハウエル(非等分散)
ゲームス=ハウエル法は,ペアとなる条件の分散が等しいという前提をおかない検定手法です。そのため,分散分析にウェルチの検定を用いた場合には,こちらの方法を用いるのが適切です。
ゲームス=ハウエル法による多重比較の結果は,図6.13のような形で示されます。

図6.13: ゲームス=ハウエル法による多重比較の結果
テューキー(等分散)
もう1つのテューキー法は,ペアとなる2つの条件で分散が等しいことを前提とした多重比較の方法です。そのため,分散分析にフィッシャーの検定を用いた場合には,こちらの方法を用いるのが適切といえます。
テューキー法による多重比較の結果も,表示のされ方はゲームス=ハウエル法の場合と同じです。この2つでは,p値が異なる場合があるだけです(図6.14)。

図6.14: テューキー法による多重比較の結果
この多重比較の結果から,今回のサンプルデータでは一致条件と文字なし条件,一致条件と不一致条件の間で平均値の差が有意であることがわかります。
統計量
最後に,「統計量」の部分を見ておきましょう。ここに含まれる項目は,多重比較結果の表示方法について設定するものです。
差が有意なペアに印
最後の「差が有意なペアに印」の項目にチェックを入れると,差が有意であった部分に「*」などの印が表示されます。これらの設定項目のすべてにチェックを入れると,結果の表示は図6.15のようになります。
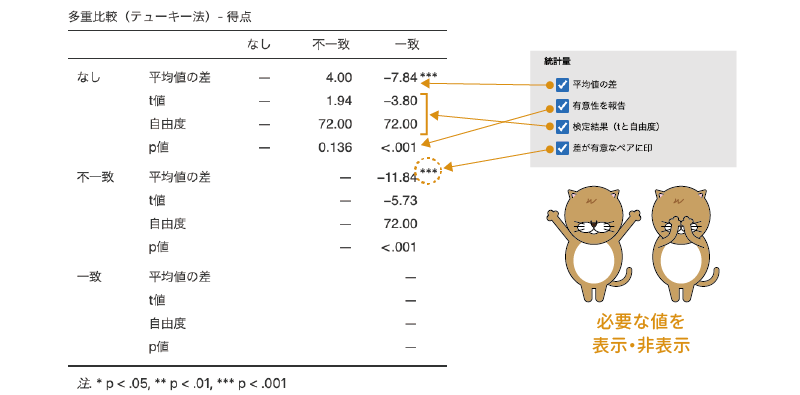
図6.15: 多重比較における検定統計量の表示設定