8.2 多値目的変数[χ²適合度検定]
変数のとりうる値が「はい・いいえ」や「あり・なし」のような2値でなく,3つ以上ある場合で,各変数値(カテゴリー)の比率について検定したい場合には,カイ2乗適合度検定と呼ばれる手法が用いられます。
8.2.1 考え方
次の例について考えてみましょう。
人の学習スタイルを大きく「視覚型(映像やイメージを利用した学習を好むスタイル)」,「聴覚型(音声を利用した学習を好むスタイル)」,「運動感覚型(運動や動作を用いた学習を好むスタイル)」の3とおりに分類したとすると,その一般的な比率は視覚型が65%,聴覚型が30%,運動感覚型が5%程度なのだそうです。
ここで,ある地域で小学生児童150人を無作為に選び,その児童の学習スタイルの判定を行ったところ,表8.3の結果が得られました。この地域の小学生における学習スタイルの比率は,一般的な比率とは異なっているのでしょうか。
| 視覚型 | 聴覚型 | 運動感覚型 | |
|---|---|---|---|
| 人数 | 89 | 48 | 13 |
| 比率 | 59.3% | 32.0% | 8.7% |
まず,この結果が想定される比率と異なるかどうかを見るためには,想定される比率の場合にどのような人数配分になるのかを知る必要があります。そこで,測定結果が想定される比率どおりであった場合に,それぞれのタイプの児童が何人ずつになると考えられるのかを考えてみましょう。一般的な比率が視覚型が65%,聴覚型が30%,運動感覚型が5%であるとした場合,150人の児童をこの比率に割り振ると表8.4のようになります。
| 視覚型 | 聴覚型 | 運動感覚型 | |
|---|---|---|---|
| 人数 | 97.5 | 45 | 7.5 |
| 比率 | 65% | 30% | 5% |
このような,想定される比率どおりに全体の人数を割り振った値は期待度数と呼ばれます。人数なのに「97.5人」と小数点を含む値になっているのは変だと思うかもしれませんが,これはあくまでも理論上の数値ですので,これで問題ありません。
そして,この状態と実際の観測データにおける人数(これを観測度数といいます)が異なるかどうかを知りたいわけですから,この期待度数と観測度数がどれだけずれているか,両者の差を求めてみます(表8.5)。
| 視覚型 | 聴覚型 | 運動感覚型 | |
|---|---|---|---|
| 観測度数 | 89 | 48 | 13 |
| 期待度数 | 97.5 | 45 | 7.5 |
| 差:観測 − 期待 | -8.5 | 3 | 5.5 |
こうしてみると,それぞれのスタイルで観測度数と期待度数にずれがあることがわかります。なお,観測度数も期待度数も合計人数は150人で同じですから,期待度数と観測度数のずれがあるということは,この2つの間で3つのスタイルの比率が異なっているということです。
そこで,このようにして求めた各スタイルにおける観測度数と期待度数のずれの大きさを1つの値にまとめ,その値を用いて観察された結果と想定される比率の間に差があるといえるかどうかを判断しようとするのがカイ2乗適合度検定の考え方です。
なお,それぞれのスタイルにおけるずれの大きさを1つの値にまとめる際,「ずれの大きさ」の値がマイナスというのは扱いづらいですので,ずれの値は2乗してマイナスが取り除かれます。また,97.5人いることが期待される視覚型と7.5人しかいないことが期待される運動感覚型とでは「1人のずれ」の大きさがもつ意味合いが同じとはいえません。そこで,これら2乗したずれの値をさらに期待度数の大きさで調整してから合計することによって,全体的なずれの大きさが求められます。このようにして求めた値は,\(\chi^2\)(カイ2乗)と呼ばれる値の分布に近似的に従うことがわかっています。
そこで,\(\chi^2\)分布を利用して,帰無仮説(母集団の比率と想定される比率の差は0である)のもとでその大きさのずれが生じる確率を計算します。そして,その確率が有意水準未満であった場合に,「母集団の比率と想定される比率は有意に異なる」と判断するのです。
8.2.2 分析手順
2項検定の場合と同様に,まずは分析用のデータを作成しましょう。先ほどの調査結果を,スプレッドシートに次のように入力してください(図8.11)。

図8.11: サンプルデータ
スタイル学習スタイル(視覚型,聴覚型,運動感覚型)人数各スタイルの人数(視覚型:89,聴覚型:48,運動感覚型:13)
データの入力が終わったら早速分析しましょう。カイ2乗適合度検定を実施するには,分析タブの「 度数分析」で「1標本比率検定」のところにある「多値目的変数[\(\chi^2\)適合度検定]」を選択します(図8.12)。
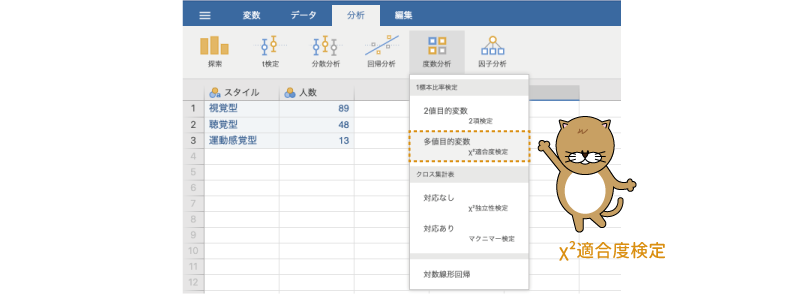
図8.12: 適合度検定の実行
すると,図8.13のような設定画面が表示されます。
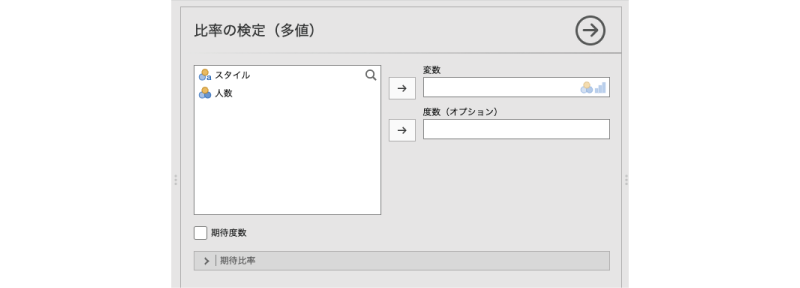
図8.13: 適合度検定の設定画面
- 変数 分析対象の変数を設定します。
- 度数(オプション) データが度数として入力されている場合に設定します。
- 期待度数 期待度数を算出します。
- 比較対象となる比率を設定します。
この画面で,「スタイル」を「変数」に移動します(図8.14)。
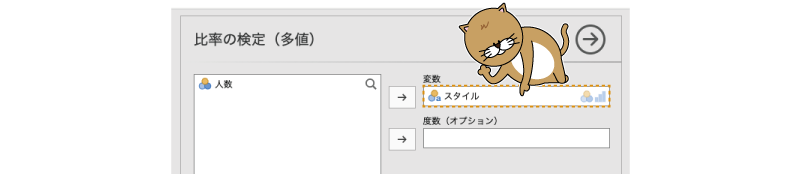
図8.14: 分析対象の変数を設定
なお今回のデータは,2項検定のサンプルデータと同じく,すでに集計済みの度数が入力されています。「スタイル」には,視覚型,聴覚型,運動感覚型の値は1つずつしか含まれていませんので,このままではうまく分析できません。
そこで,各スタイルの度数が入った変数(「人数」)を「度数(オプション)」のところへ移動して,jamoviがそれぞれのスタイルの人数を認識できるようにします(図8.15)。この操作は,集計済みでないデータ(各個人の値が1行ずつ入力されているデータ)の場合には必要ありません。
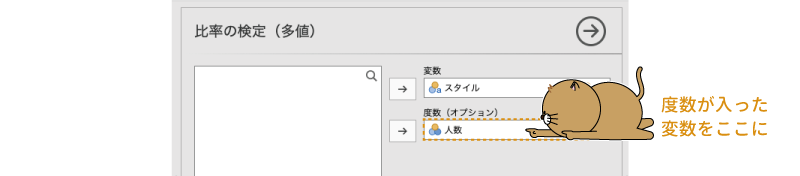
図8.15: 各スタイルの度数を設定
これで分析の設定は終わりですといいたいところですが,このままではどのような比率とデータを比較するのかがわかりません。そのままでは適切な分析結果が得られませんので,比較対象となる比率を設定してやる必要があります。
8.2.3 期待比率
比較対象となる比率を設定するには,を展開し,各変数値の「比率」のところに適切な数値を入力します(図8.16)。なお,日本語訳では真ん中の欄と一番右の欄がどちらも「比率」と表示されていますが,値を入力できるのは真ん中の欄のみです。真ん中の欄は正確には「比」で,ここに入力した数値をもとに計算された比率が一番右の欄に表示されます。
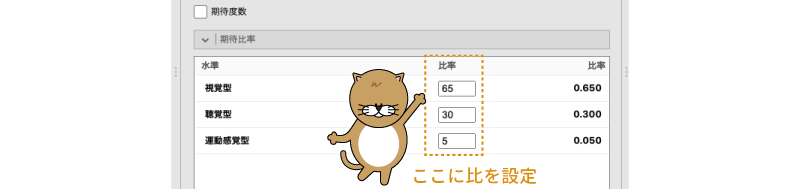
図8.16: 各スタイルの度数を設定
今回の例では,期待される割合は視覚型が65%,聴覚型が30%,運動型が5%ですので,「視覚」の比に「65」,「聴覚」に「30」,「運動」に「5」を入力します。すると,その右の「比率」欄に,それぞれの型の比率が表示されます。入力の際には「水準」欄をよく確認し,入力する行を間違えないように注意しましょう。
なお,今回は使用しませんが,この設定を行ったあとに,のすぐ上にある「期待度数」にチェックを入れると,指定した比率における期待度数を結果に表示させることもできます。
これで分析の設定は終了です。
8.2.4 分析結果
カイ2乗適合度検定の結果は次のような形で表示されます(図8.17)。
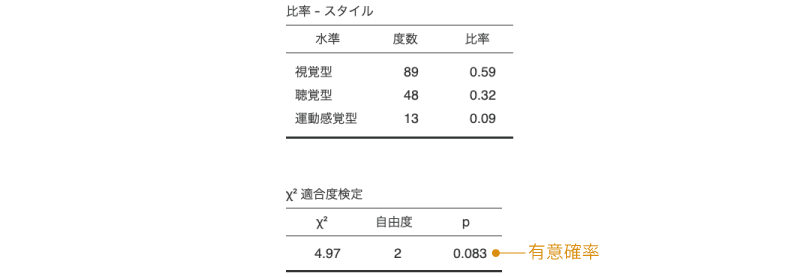
図8.17: 適合度検定の分析結果
結果の1つ目の表は,観測データについての度数分布表です。今回は集計された度数をデータとして入力しましたが,1人1人の値が入力されているデータで分析を行う場合には,この度数分布表で各水準(変数値)の度数をよく確認しておきましょう。
その下の2つ目の表が適合度検定の結果です。適合度検定の結果の表には,検定統計量(\(\chi^2\))と自由度,そして有意確率(p)の値が示されています。この表のpの値が有意水準を下回る場合に,このデータの母集団の比率が想定される比率と有意に異なると判断します。
今回の分析結果ではp = 0.083ですので,このデータ(小学生児童150人)の母集団における比率は,想定されている比率と有意に異なるとはいえません。