8.4 対応あり[マクニマー検定]
無作為に選抜した生徒100人を対象に,本試験用の問題と追試験用の問題の両方を解いてもらい,それぞれ何人が合格基準に達するかを調べたところ表8.12の結果が得られたとしましょう。
| 本試験 | 追試験 | 計 | |
|---|---|---|---|
| 合格 | 68 | 79 | 147 |
| 不合格 | 32 | 21 | 53 |
| 計 | 100 | 100 | 200 |
そしてこの結果から,試験問題の違いによって合格・不合格の程度が異ならない(どちらも難易度が同程度になっている)かどうかを確かめたいとします。この場合,どのように分析すればよいでしょうか。
このデータは,一見すると独立性の検定で分析できそうに見えるのですが,残念ながらそうではありません。なぜなら,このデータでは「本試験」と「追試験」の両方に同じ人のデータが含まれているからです。これはいわゆる「対応あり」のデータで,データ収集方法にそもそも対応があるわけですから,それに対して「独立」かどうかという検定を行っても適切な結果が得られないのです。
このような場合,次にとりあげるマクニマー検定と呼ばれる検定が用いられます。
8.4.1 考え方
先ほどのクロス集計表は,残念ながらそのままでは分析ができません。このようなデータの場合には,クロス集計表は本試験の合否を行に,追試験の合否を列に配置するような形で作成する必要があります。
そこで,もう一度全員の結果を調べ直し,分析に適した形でクロス集計表を作成し直したところ,表8.13のようになったとします。
| 合格 | 不合格 | 計 | |
|---|---|---|---|
| 本試験 | |||
| 合格 | 58 | 10 | 68 |
| 不合格 | 21 | 11 | 32 |
| 計 | 79 | 21 | 100 |
この表は先ほどの表と似ていますが,先ほどの表は総度数が200だったのに対し,この表は総度数が100で,調査対象の人数と同じになっています。つまり,先ほどの表はデータの対応がまったく考慮されていなかったのに対し,こちらはデータの対応をきちんと考慮した形で集計表が作成されているのです。
次に,本試験と追試験で難易度が同じである場合の期待度数について考えてみましょう。ここでは,考え方についてみるために,それぞれのセルの度数をa〜dで表しています(表8.14)。
| 合格 | 不合格 | 計 | |
|---|---|---|---|
| 本試験 | |||
| 合格 | a | b | a+b |
| 不合格 | c | d | c+d |
| 計 | a+c | b+d | 100 |
2つの試験の難易度が同じであれば,本試験で合格できた人は追試験でも合格するはずです。つまり,「a+b」の人数と「a+c」の人数は同じになるはずです。同様に,本試験で合格できなかった人は追試験でも合格できないはずで,その場合には「c+d」と「b+d」の人数も同じになります。
そして,これらの関係を整理すると,合格の度数についての「a+b = a+c」という関係は,結局は「b = c」ということですし,また,不合格の度数についての「c+d = b+d」というのも,結局は「b = c」ということになって,2つの試験で難易度が同じである場合に期待されるのは,「b = c」の状態ということになります。
そこで,マクニマー検定では,観測データにおける右上のセルと左下のセルの値が互いにどれだけずれているかを検定統計量として算出し,そこから2つの試験の難易度に違いがあるといえるかどうかを判断します。
8.4.2 分析手順
ここでは,次のサンプルデータ(frequencies_data05.omv)を用いて分析を行いましょう。このデータファイルには次の変数が含まれています(図8.49)。
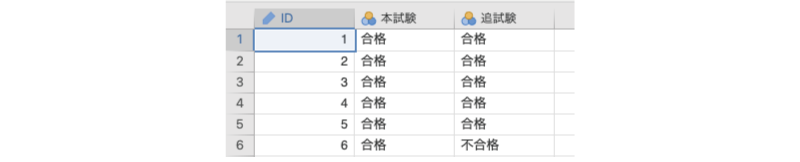
図8.49: サンプルデータ
ID生徒のID本試験本試験の合否(合格,不合格)追試験追試験の合否(合格,不合格)
ここでは,各生徒の本試験と追試験の結果が入力されたデータファイルを使用しますが,すでに集計済みのデータで分析を行う場合,スプレッドシートには図8.50のような形でデータが入力されている必要があります。

図8.50: 集計済みデータの入力方法
マクニマー検定を実施するには,分析タブの「 度数分析」で「クロス集計表」のところにある「対応あり[マクニマー検定]」を選択します(図8.51)。
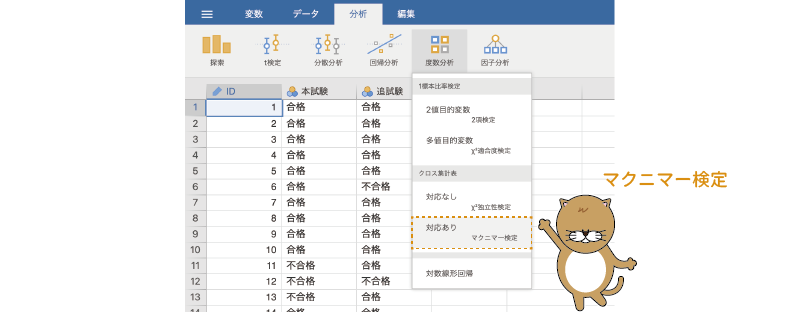
図8.51: マクニマー検定の実行
すると,図8.52のような画面が表示されます。
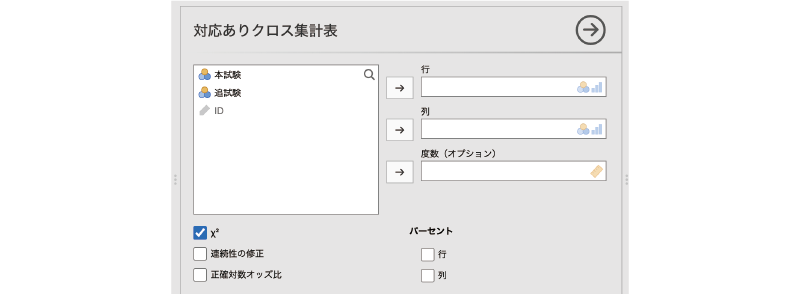
図8.52: マクニマー検定の設定画面
- 行 クロス集計表の行に配置する変数を指定します。
- 列 クロス集計表の列に配置する変数を指定します。
- 度数(オプション) 度数が含まれている変数を指定します(オプション)
- \(\chi^2\) \(\chi^2\)値を算出します。
- 連続性の修正 連続性の修正を行った\(\chi^2\)値を算出します。
- 正確対数オッズ比 対数オッズ比と正確確率検定の結果を表示します。
- パーセント
- 行 各行におけるパーセント値を算出します。
- 列 各列におけるパーセント値を算出します。
ここでは,「本試験」を「行」に,「追試験」を「列」に設定しましょう。このデータファイルには一人一人の結果が入力されているので,分析の基本設定はこれで終わりです。「度数(オプション)」の設定は必要ありません。集計済みデータで分析をする場合には,度数が入力されている変数を「度数(オプション)」に指定してください(図8.53)。
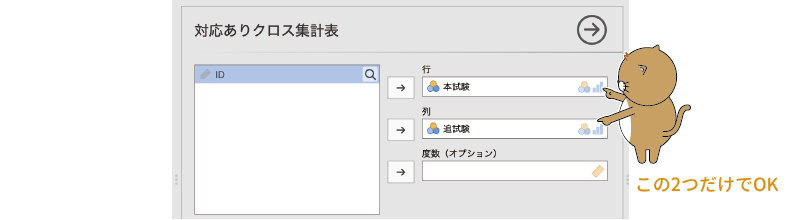
図8.53: マクニマー検定の分析設定
8.4.3 分析結果
それでは結果を見てみましょう(図8.54)。
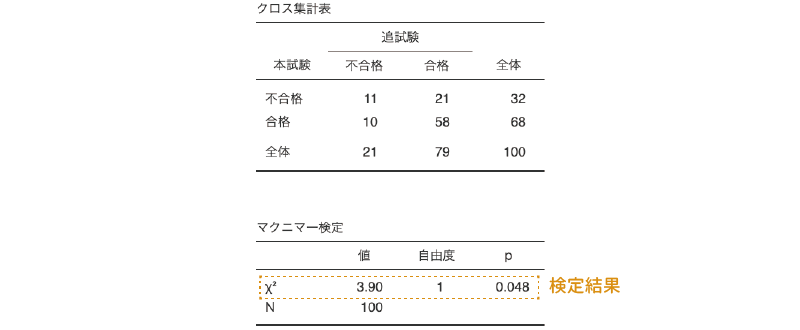
図8.54: マクニマー検定の結果
結果の表示,および見方は,独立性検定の場合とほぼ同じです。1つ目の表はクロス集計表,2つ目の表が検定結果です。\(\chi^2\)値の有意確率は5%の有意水準を下回っているので(p = 0.048),検定結果は有意です。つまり,本試験と追試験で難易度(合格・不合格の比率)が異なるということになります。
8.4.4 分析オプション
マクニマー検定では利用可能な分析オプションは多くありません。分析に関する設定項目は,検定統計量としてイェーツの修正を行った\(\chi^2\)を算出する項目と,対数オッズ比を算出するための項目だけです。連続性の修正を行った\(\chi^2\)は,独立性検定の場合と同じですので説明は省略します。
検定オプションの「正確対数オッズ比」は,正確確率を用いた検定結果を表示します(図8.55)。この方法を用いて分析した場合に表示される「正確対数オッズ比」の値は,クロス集計表の右上および左下のセルの度数について帰無仮説どおりの場合の比率と観測データにおける比率から算出したオッズ比の対数です。

図8.55: 対数オッズ比と正確確率検定の結果
マクニマー検定では,右上のセルと左下のセルの度数だけを考え,そしてこの2つのセルの度数は同じというのが帰無仮説ですので,右上のセルの左下のセルに対するオッズは「1/1 = 1」となります。そして,今回のデータでは,右上のセルは31人中10人(10/31 = 0.32),左下のセルは31人中21人(21/31 = 0.68)なので,右上のセルのオッズは「0.32/0.68 = 0.47」となります。
この場合,帰無仮説のオッズを基準(分母)としたオッズ比は「0.47/1 = 0.47」で,これを対数変換すると「log 0.47 = \(-\textsf{0.76}\)」となります。途中で四捨五入しながら計算しているので結果の表に表示されている値と完全には一致しませんが,このように計算するとほぼ同じ値になるのがわかります。
また,マクニマー検定はクロス集計表の右上のセルと左下のセルの度数が同じかどうかを検定していますので,考え方としては,この2つのセルの出現比率が1:1になっているかどうかを2項検定するのと同じことになります。この検定における有意確率pの値は,「31人中10人」という結果について2項検定を行った場合の値に一致します。
設定画面右側の「パーセント」の項目は,クロス集計表にパーセントを表示するかどうかの設定です。「行」をチェックすれば行ごとのパーセント値が,「列」をチェックすれば列ごとのパーセント値が表示されます。