7.5 多値従属変数[多項]
次のサンプルデータ(regression_data04.omv)を見てください。このデータには,成人200名分の,その人がもつ愛着スタイル(安定型,不安型,回避型)と,性格検査による性格主要5因子の測定値が記録されています(図7.86)。
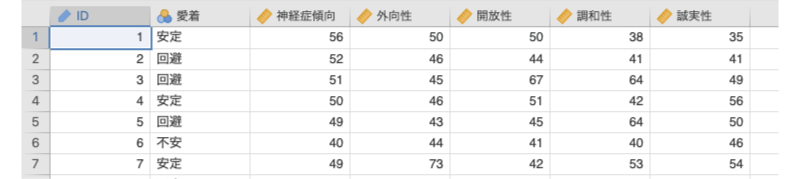
図7.86: サンプルデータ
ID対象家族のID愛着愛着スタイル(安定,不安,回避)神経症傾向神経症傾向の得点外向性外向性の得点開放性開放性の得点調和性調和性の得点誠実性誠実性の得点
ここで,成人の愛着スタイルに性格の主要5因子(神経症傾向,外向性,開放性,調和性,誠実性)がどのように影響しているかを回帰分析を使って分析したいとしましょう。さて,どのようにすればよいのでしょうか。
この場合,愛着スタイルを従属変数とし,性格の主要5因子を予測変数とする回帰分析を行うことになりますが,この場合の従属変数は,「安定・不安・回避」の3種類の値をもつ名義型変数です。このように,従属変数が名義尺度による測定値で,その値に3つ以上のカテゴリーが含まれる場合には,多項ロジスティック回帰分析と呼ばれる分析手法が用いられます。
7.5.1 考え方
多項ロジスティック回帰は,2項ロジスティック回帰を拡張して2値変数以外にも適用できるようにしたもので,その基本的な考え方は2項ロジスティック回帰と同じです。多項ロジスティック回帰では,3種類以上ある従属変数の値のうちの1つを基準としたロジスティック回帰モデルを,従属変数の種類(カテゴリー)より1つ少ない数だけ作成します。
たとえば,今回のサンプルデータの場合,従属変数は「安定」,「不安」,「回避」の3種類ですので,たとえば「安定」を基準として考えた場合,次の2とおりの回帰モデルを作成することになります。
従属変数の値が「安定・不安」のロジスティック回帰分析モデル
\[ \log\left(\displaystyle\frac{p(\text{不安})}{p(\text{安定})}\right) = b_{10} + b_{11} \times N+ b_{12} \times E+ b_{13} \times O+ b_{14} \times A+ b_{15} \times C \]
従属変数の値が「安定・回避」のロジスティック回帰分析モデル
\[ \log\left(\displaystyle\frac{p(\text{回避})}{p(\text{安定})}\right) = b_{20} + b_{21} \times N+ b_{22} \times E+ b_{23} \times O+ b_{24} \times A+ b_{25} \times C \]
そして,これら2つのロジスティック回帰モデルについて同時に係数を推定するのです。
7.5.2 分析手順
基本的な考え方は2項ロジスティック回帰と大きく変わりませんので,まずは分析してみることにしましょう。多項ロジスティック回帰を行うには,分析タブの「 回帰分析」から「ロジスティック回帰」の下にある「多値従属変数[多項]」を選択します(図7.87)。
図7.87: 多項ロジスティック回帰分析の実行
すると,図7.88のような分析設定画面が表示されます。分析設定画面の構成や項目は,ロジスティック回帰分析の場合とほとんど同じです。
図7.88: 多項ロジスティック回帰分析の設定画面
まず,「従属変数」に従属変数である「愛着」を,「共変量」に連続型予測変数である性格5因子の得点(「神経症傾向」,「外向性」,「開放性」,「調和性」,「誠実性」)を設定します(図7.89)。今回のサンプルデータにはありませんが,予測変数に名義型変数が含まれている場合には,それらは「因子」に設定してください。
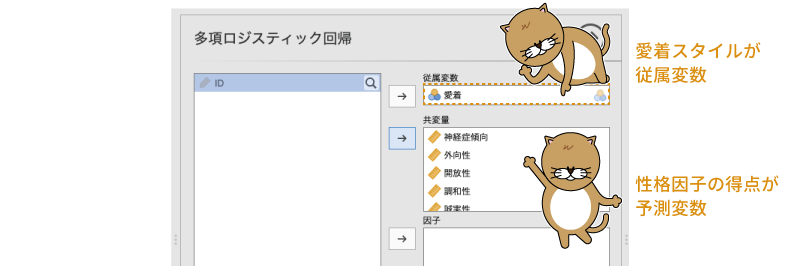
図7.89: 多項ロジスティック回帰分析の変数設定
これで基本的な分析の設定はおしまいです。ただし,2項ロジスティック回帰の場合と同様に,多項ロジスティック回帰の場合にも従属変数のどの値を基準として結果が計算されているのかによって数値の意味が変わってきますので,でそれらを確認しておいたほうがよいでしょう(図7.90)。

図7.90: 従属変数の基準レベルの確認
ここでは「安定」を基準に分析することにします。もし基準レベルが違う値になっていたら,「安定」を選択して設定してください。これで分析はおしまいです。モデルの適合度指標や係数の信頼区間,検定などは2項ロジスティック回帰の場合と同じですので,ここでは説明を省略します。また,多項ロジスティック回帰の場合には,前提条件のチェック,予測,計算結果の保存の設定項目は(今のところ)ありません。
7.5.3 分析結果
結果は図7.91のような形で表示されます。
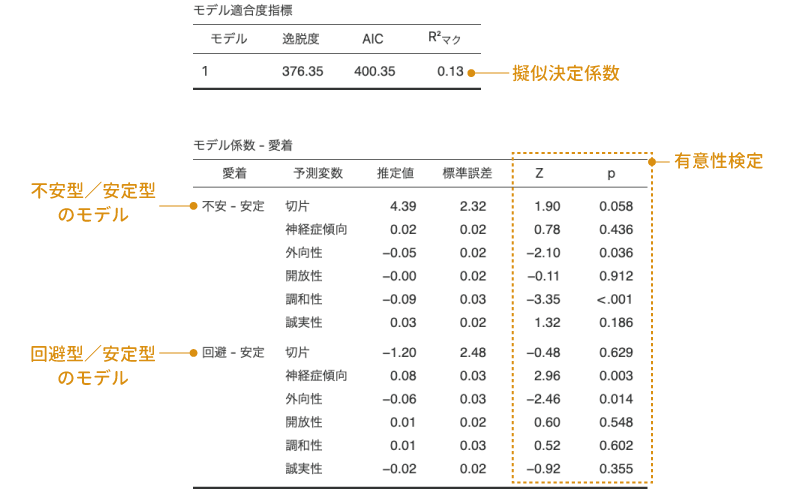
図7.91: 多項ロジスティック分析の結果
モデルの適合度指標として逸脱度やAIC,擬似決定係数などが算出される点は2項ロジスティック回帰の場合と同じです。また,モデル係数の表についても,基本は2項ロジスティック回帰の場合と同じです。ただし,多項ロジスティック回帰では複数のモデルについて同時に係数の推定を行いますので,係数の推定値についてはそれらのモデルごとに表示されるという点が異なります。
分析結果を見てみると,「不安型/安定型」のモデルでは「外向性」と「調和性」がそれぞれ有意に負の影響を持っていることがわかります(外向性の回帰係数は\(-\textsf{0.05}\),調和性は\(-\textsf{0.09}\))。このことから,外向性が低い人,調和性が低い人ほど不安型の愛着スタイルである可能性が高いといえそうです。
また,「回避型/安定型」のモデルでは「神経症傾向」と「外向性」の係数が有意で,神経症傾向はプラスの係数(0.08),外向性はマイナスの係数(\(-\textsf{0.06}\))ですから,神経症傾向が強く外向性が低い人ほど回避型の愛着スタイルになりやすいと考えられます。
なお,この分析では「安定」型の愛着スタイルを基準として計算を行っているため,「不安」型と「回避」型の違いについてはわかりません。その違いを見たい場合には,不安型か回避型のいずれかを基準レベルとして再度分析する必要があります。