6.5 多変量共分散分析
たとえばストレスの測定などにおいては,血圧と筋電図など,同時に複数の指標を用いることがあります。それらの指標に対し,実験条件の主効果や交互作用があるといえるかどうかを確かめたい場合,分散分析では一度に1つの指標しか分析に用いることができません。
この場合,それぞれの指標が互いにまったく無関係(独立)なものであれば,それぞれの指標について個別に分散分析を行うといった方法でよいでしょう。しかし,それら複数の指標の間に関連性があり,そしてそれらをひとまとまりとして分析したい場合には,分散分析は使えません。
そのような場合の分析手法の1つとして,分散分析を多変量に拡張した多変量分散分析(MANOVA)があります。通常の分散分析が従属変数を1つしか扱えないのに対し,多変量分散分析では複数の従属変数を一度に分析することが可能です。また,共変量の影響を取り除いたうえで主効果や交互作用について分析する分散分析は共分散分析と呼ばれますが,多変量分散分析でもこれと同様のことが可能です。多変量分散分析で共変量を用いる場合の分析は,多変量共分散分析(MANCOVA)と呼ばれます。
ここでは,この多変量共分散分析の考え方について簡単に見ておくことにしましょう。なお,多変量共分散分析でも交互作用の分析は可能ですが,話が複雑になるのでここでは主効果のみを考えることにします。
6.5.1 考え方
履修者数が100人を超えるような大規模な講義科目において,通常の教室での講義とオンラインでの講義の間で学生の満足度や理解度に違いがあるかどうかを調べたいとします。そこで,教室で実施されている授業とオンラインでリアルタイムに実施するライブ形式の授業,オンデマンドで動画配信を行う形式の授業のそれぞれから無作為に30科目を選び,それらの科目で満足度と理解度を測定しました。その結果がこのサンプルデータ(anova-data05.omv)です(図6.79)。
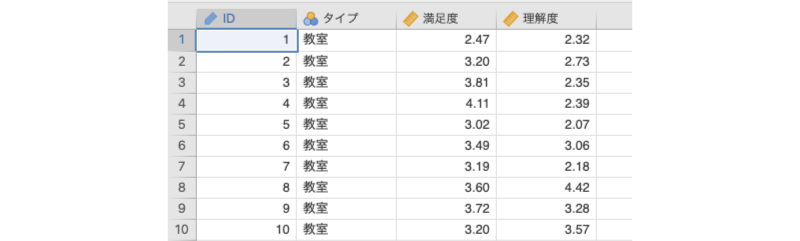
図6.79: サンプルデータ
ID授業のIDタイプ授業のタイプ(教室,ライブ,オンデマンド)満足度その授業に対する受講生の満足度評価(1〜5)の平均値理解度その授業に対する受講生の理解度(1〜5)の平均値
このデータでは,各授業について満足度と理解度の2種類の測定値(いずれもその授業の受講者による評価の平均値)があります。そして,この2種類の測定値が,授業のタイプ(教室,ライブ,オンデマンド)によって異なるかどうかを知りたいわけです。この場合,授業の満足度と理解度の評価がまったく無関係ということはおそらくないでしょう。
ですので,できれば満足度と理解度で別々に分析するのではなく,これら2つの評価値をひとまとめにして,3つの授業タイプの間に全体的な違いがあるかどうかを見たいと思います。さて,その場合にはどうすればよいのでしょうか。
これについて,まずはもっと単純化した形で考えてみましょう。正規分布した母集団が1つあるとします。その母集団の分布を,横軸に変数値,縦軸に度数をとって表すと,図6.80のようなおなじみの形になります。
図6.80: 正規分布の母集団
今度は,相関関係がある2つの母集団の分布を見てみましょう。正規分布する2つの母集団の間に明確な正の相関があるとき,1つ目の変数値を横軸,2つ目の変数値を縦軸にとって散布図の形に示すと図6.81のようになります。これもおなじみの形です。

図6.81: 相関のある母集団の散布図
さて,この散布図には,それぞれの値の度数は示されていません。そこで,このように相関がある母集団の分布について,度数を高さとする形で図示してみます。すると,その形は図6.82のようになります。先ほどの散布図は,この立体的な山を真上から眺めたものといえます。また,このような正規分布する複数の変数で構成された分布は多変量正規分布と呼ばれます。

図6.82: 相関関係のある母集団の度数の分布
ここで,サンプルデータのように2つの変数で構成される多変量正規分布が3つあったとしましょう。そして,それらを1つの散布図に示したところ,図6.83のようになったとします。

図6.83: 3つの多変量正規分布の散布図
この3つの分布の山を,変数1,変数2の軸からそれぞれ眺めた場合,その分布の形は図6.84のようになります。このように,同じ分布であっても,それらをどの方向から見るかによって,その見え方が大きく異なるのがわかります。
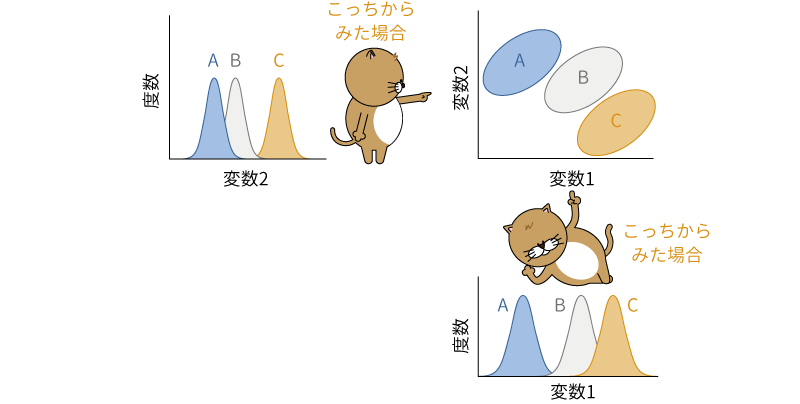
図6.84: 3つの多変量正規分布の視点による違い
この変数1から見た場合の分布は,3つの母集団における変数1の分布と同じものです。たとえばこのデータで,変数1の平均値に3つの母集団で差があるといえるかどうかを分散分析で確かめたとすると,この図におけるA,B,Cそれぞれの平均値のばらつきが主効果,それぞれの母集団の中での値のばらつきを総合したものが残差(誤差)ということになります。
先ほどの変数1からの視点,変数2からの視点の分布をもう一度よく見てみると,変数1の視点では,Aの分布がBとCに比べてやや離れているように見えますが,変数2の分布では,A,Bの分布とCの分布の間に差がありそうに見えます。また,変数2の分布はそれぞれの母集団内でのばらつきの幅が小さい(山の幅が狭い)のに対し,変数1の分布では,変数2に比べてそれぞれの母集団におけるばらつきの幅が少し広くなっています。このように,同じ3つの分布であっても,見る視点が異なれば,その平均値やばらつきの幅の見え方は異なってくるのです。
母集団A,B,Cの違いの見え方がその分布を眺める角度によって異なるのであれば,この3つの分布の違いがわかりやすくなるような視点があるかもしれません。たとえば,図6.85のような斜めの視点からこれらの分布を眺めてみるとどうでしょう。すると,A,B,Cの3つでそれぞれに平均値(山の頂上)の位置が異なり,また,各分布における値のばらつき幅は非常に狭くなっていて,この3つの分布の違いがとてもよくわかるようになりました。
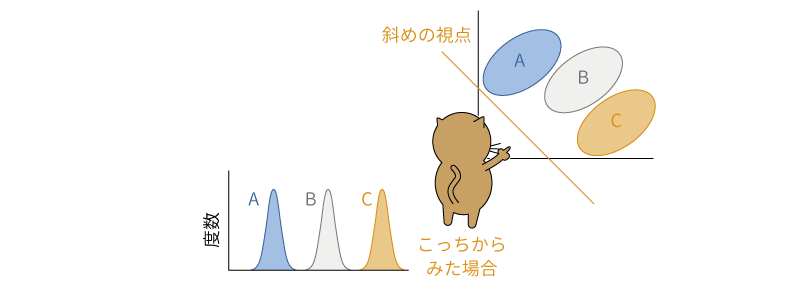
図6.85: 3つの分布を別の視点から眺めた場合
このようにして,多変量共分散分析では,分布の違いがもっとも明確になる視点からこれら多変量の分布を眺め,そしてその視点における各条件の平均値のばらつき(主効果)と,それぞれの分布内での値のばらつき(残差)を算出します。あとは分散分析の考え方と同じで,主効果のばらつきが残差(誤差)のばらつきに比べてどの程度大きいかをもとに,帰無仮説(すべての条件で分布は同じ)を棄却すべきかどうかについて判断します。
6.5.2 分析手順
多変量共分散分析は,分析タブの「 分散分析」から「多変量共分散分析」を選択して実施します(図6.86)。
図6.86: 多変量共分散分析の実行
すると,図6.87のような設定画面が表示されます。「分散分析」などに比べると,かなりシンプルな設定画面です。
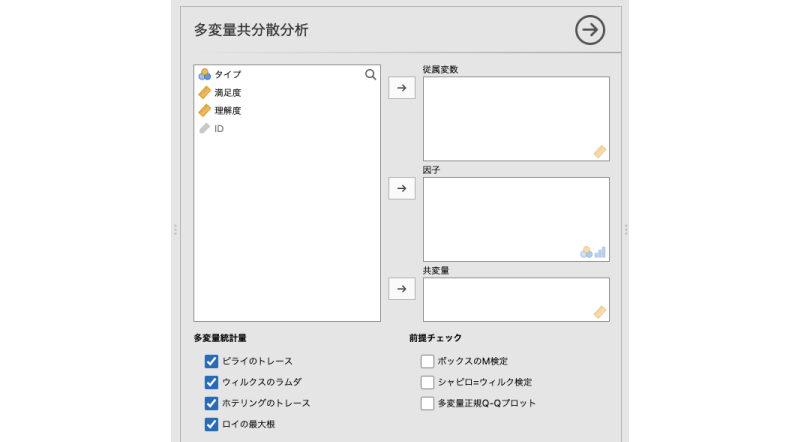
図6.87: 多変量共分散分析の設定画面
ここで,「満足度」と「理解度」の2つの従属変数を「従属変数」に,授業の「タイプ」を「因子」に移動します。今回の分析では「因子」として用いるのは授業タイプの1つのみですが,複数の要因を用いた分析の場合には,それらをすべてここに移動します(図6.88)。
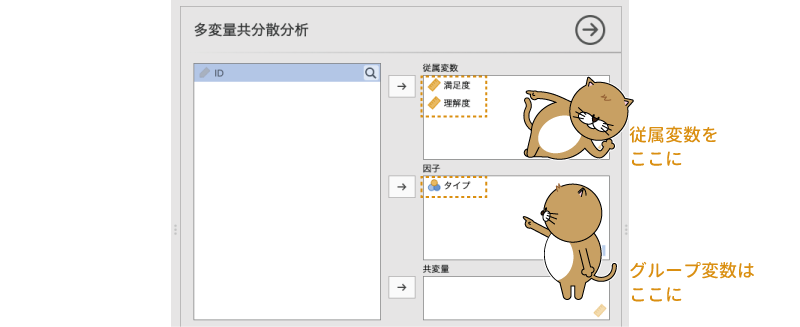
図6.88: 多変量共分散分析の分析設定
また,今回のデータには共変量は含まれていませんので,「共変量」の部分は空欄のままです。つまりこのデータの場合の分析は,多変量共分散分析の「共」がないタイプ,すなわち多変量分散分析ということになります。
分析の基本設定はこれだけで,これで分析の結果が出力されます。
6.5.3 分析結果
多変量共分散分析の結果は,図6.89のような形で表示されます。
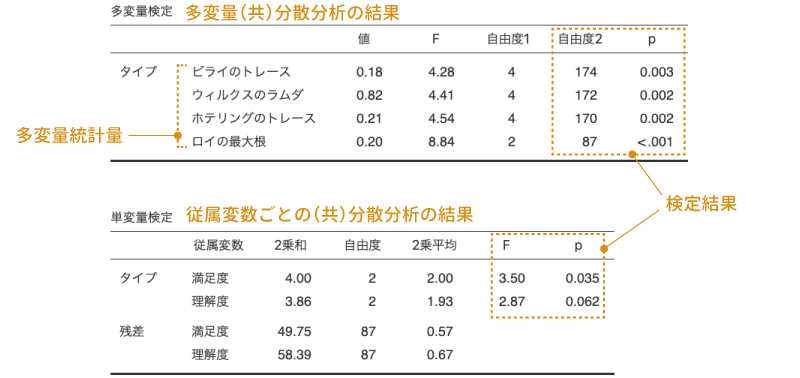
図6.89: 多変量分散分析の分析結果
結果の1つ目の表が,多変量分散分析の結果です。表には,多変量統計量の「値」とそれらの値を元に算出した「F」,主効果と残差それぞれの自由度(自由度1,自由度2),そして有意確率(p)が示されています。主効果は1つなのに4つもpの値が表示されていますが,これは多変量分散分析における統計量の算出方法に複数の考え方があるためです。
これら4つの値のうち,一般には「ウィルクスのラムダ」と呼ばれる値に基づく結果で判断することが多いようですので,ここでもそうすることにしましょう。すると,統計量Fの値は4.41で,このFの有意確率はp=0.002ですので主効果は有意です。つまり,授業タイプによって,満足度や理解度に違いがあるということになります。
結果の2つ目の表は,それぞれの従属変数ごとに分散分析を実施した結果が示されています。多変量共分散分析の場合,複数の従属変数を総合した形で分析しているので,そこで主効果が有意であったとしても,それがどのような差を表しているのかがわかりません。そこで,多変量共分散分析が有意であった場合には,その次の段階として,複数の従属変数のそれぞれについて個別に分析を行うという方法が一般的に用いられます。
なお,多変量の結果で主効果が有意でなくても,単変量(個別の分析)の分析結果に主効果が有意なものが含まれている場合があるかもしれませんが,多変量での検定結果が有意でない場合には,それらの個別の分析結果は使用しません。これは,分散分析で主効果が有意でない場合には多重比較を行わないのと同じ理由です。
さて,この単変量の分散分析結果からは,3つの授業タイプの間では,理解度と満足度のうち,満足度の方に何か違いがありそうだということがわかります。
6.5.4 分析の詳細設定
jamoviの「多変量共分散分析」で提供されている機能はごく基本的もののみなので,設定できる項目は多くありません。設定可能なのは,算出される多変量統計量の種類の選択と,分析の前提に関するチェックのみです。
多変量統計量
設定画面の多変量統計量には,次の4つの項目が含まれています。
- ピライのトレース
- ウィルクスのラムダ
- ホテリングのトレース
- ロイの最大根
多変量共分散分析でも,分散分析の場合と同様に,主効果のばらつきが残差のばらつきに比べてどの程度大きいかを元に結果の判断を行うのですが,分散分析における主効果や残差の値は,多変量の分析ではすべて行列8の形で扱われます。その場合,主効果が残差に比べてどれだけ大きいかを評価する方法には複数の考え方があり,その代表的なものがこれら4つの値なのです。
なお,多変量共分散分析では,これらの統計量を分散分析で使用する統計量Fに近似したうえで検定を行うのが一般的です。そのため,jamoviの分析結果でも,それぞれの値をFに変換したものが結果の表に記載されています。
ピライのトレース
ピライのトレースは,主効果の2乗和の行列にデータ全体の(偏差の)2乗和の行列の逆行列を掛け合わせた結果に基づく統計量です。「逆行列」というのは,ある数値(x)に対する逆数(1/x)に相当するもので,逆行列を掛けるということは,通常の計算における割り算のような処理を行っていることになります。つまり,非常におおざっぱにいえば,この処理は主効果の2乗和をデータ全体の偏差2乗和で割っているようなものといえます。
ピライのトレースの「トレース」とは,行列における対角成分(相関行列だとつねに1.00になる部分)の値のことです。ピライのトレースは,先ほど述べたような形で計算した結果行列の対角成分に含まれる値を合計した値です。この値は0から1までの範囲をとり,値が1に近いほど主効果が残差に比べて大きいことを意味します。
ウィルクスのラムダ
ウィルクスのラムダ(\(\Lambda\))は,多変量共分散分析においてもっとも一般的に用いられる統計量です。この値は,残差2乗和行列の行列式9をデータ全体の偏差2乗和の行列の行列式で割って算出されます。ピライのトレースでは主効果を全体で割るような形で計算するのに対し,ウィルクスのラムダは残差を全体で割るような形での計算が行われます。そのため,このウィルクスのラムダの値は0に近いほど残差が少ない,つまり主効果が残差に比べて大きいことを意味します。
なお,jamoviでは多変量共分散分析で効果量を算出できませんが,多変量共分散分析において一般的に用いられる効果量である「多変量イータ2乗(多変量\(\eta^2\))」は,「1 − ウィルクスのラムダ」という計算によって簡単に算出することができます。
ホテリングのトレース
ホテリングのトレースも,ピライのトレースと同様に,計算の結果得られた行列のトレース(対角成分の合計)を用いて主効果の大きさを評価します。ホテリングのトレースでは,主効果の2乗和の行列に残差2乗和行列の逆行列を掛け合わせる形で計算を行います。つまり,主効果の2乗和を残差の2乗和で割るような形で主効果の大きさを評価するわけです。そのため,この値が大きいほど主効果が残差に比べて大きいということになります。なお,ピライのトレースやウィルクスのラムダは0から1の範囲の値になるのに対し,ホテリングのトレースの値は1より大きくなる場合もあります。
ロイの最大根
ロイの最大根と呼ばれる統計量の計算手順は,結果の行列を算出するところまではホテリングのトレースと同じで,主効果の2乗和行列に残差2乗和行列の逆行列を掛ける形で計算を行います。そしてロイの最大根では,その行列の固有値を計算し,その固有値の中で最大の値を統計量として用います10。
前提チェック
「多変量共分散分析」の前提チェックには,次の3つの項目が含まれています。
- ボックスのM検定
- シャピロ=ウィルク検定
- 多変量正規Q-Qプロット
ボックスのM検定
ボックスのM検定は,「すべてのグループにおいて分散共分散行列が等しい」という帰無仮説について検定を行います。この検定は,通常の分散分析における分散の等質性検定に相当するものです。多変量共分散分析の場合には,このようにグループ(水準)間で分散共分散行列が等質であるということが前提条件の1つになります。
「ボックスのM検定」のチェックをオンにすると,図6.90のような形で検定結果が表示されます。

図6.90: ボックスのM検定の結果
結果の表には,\(\chi^2\)(カイ二乗)統計量と自由度,そして有意確率pが示されています。この検定では「すべてのグループで分散共分散行列が同じ」が帰無仮説ですので,この検定の結果が有意である場合には,分析のための前提が満たされていないということになります。今回のこの結果では,ボックスのM検定の結果は有意ではありませんので,前提が満たされていないということはなさそうです。
6.5.5 多変量の多重比較
「多変量共分散分析」の設定項目はこれですべてですが,最後に多変量共分散分析で主効果が有意であった場合の事後検定について少しだけ見ておきましょう。jamoviの「多変量共分散分析」では,多変量共分散分析の結果と合わせて単変量,つまり各従属変数ごとの(共)分散分析の結果が表示されます。これはこれでよいのかもしれませんが,研究の目的によっては,従属変数ごとに個別に分析するのではなく,多変量のままで多重比較を行いたい場合もあるでしょう。そこで,そのような場合を想定した分析方法をここで見ておこうと思います。
jamoviの「多変量共分散分析」のメニューには多変量の多重比較の設定項目はありませんが,これはjamoviが標準で備えている「フィルタ」機能を用いることで実現可能です。それでは,今回のデータで多変量の多重比較を行ってみましょう。
まず,分析の設定画面を閉じ,データタブから「フィルタ」を選択します(図6.91)。

図6.91: フィルタを選択
ここで多重比較のためのフィルタ作成します。まずは「教室」の授業と「ライブ」授業の組み合わせについてのフィルタを作成しましょう。「フィルタ1」の条件式の部分に,次のとおりに入力します。
= タイプ == 1 or タイプ == 2
式の途中の「イコール」は,「=」でなく「==」と2つ続ける必要があるので注意してください。また,「or」は小文字で入力してください。変数名は関数ボタン()を使って入力するのが確実ですが,キーボードから入力しても問題ありません。
なお,ここでは授業のタイプをデータ値(1,2,3)で指定しましたが,これをラベル(教室,ライブ,オンデマンド)で指定したい場合や,あるいは変数値が文字で入力されている場合には,「“教室”」や「“ライブ”」のように,それらの値を引用符で囲む必要がありますので,この点にも注意してください。
それから,あとでこれが何のためのものかわからなくならないように,「説明」の部分には「教室 - ライブの比較」のようにして説明を記入しておくとよいでしょう(図6.92)。
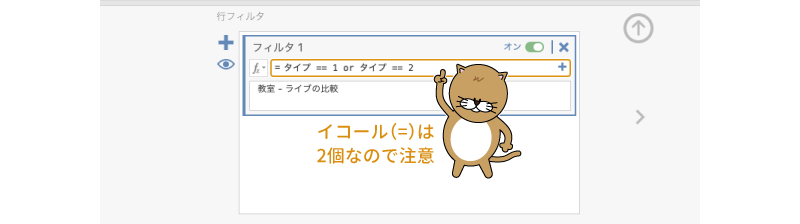
図6.92: フィルタの設定
これでこのペアについての比較は可能ですが,ついでなので他の組み合わせについてもここでフィルタを作成しておきます。「教室」と「オンデマンド」の比較用フィルタを作成するには,「」の上にあるほうの「
」をクリックしてください(図6.93)。
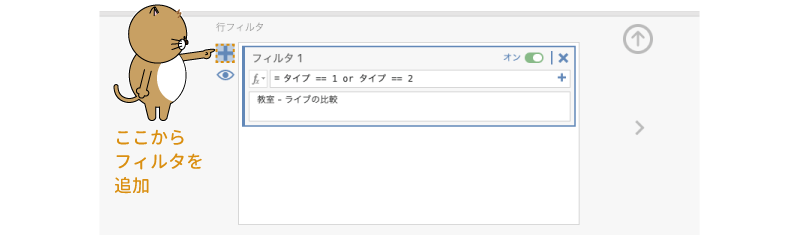
図6.93: フィルタの追加
そして,条件式に次の内容を入力します(図6.94)。
= タイプ == 1 or タイプ == 3
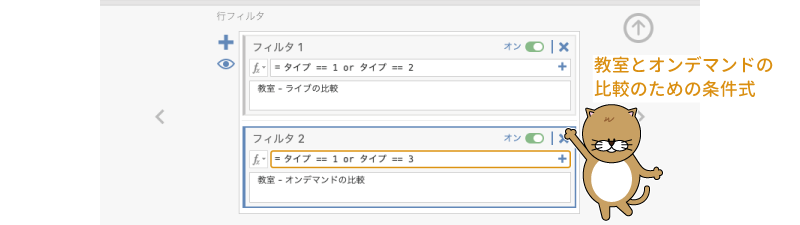
図6.94: 「教室」と「オンデマンド」の比較用フィルタ
同様にして,「ライブ(2)」と「オンデマンド(3)」の比較用のフィルタも作成しましょう(図6.95)。
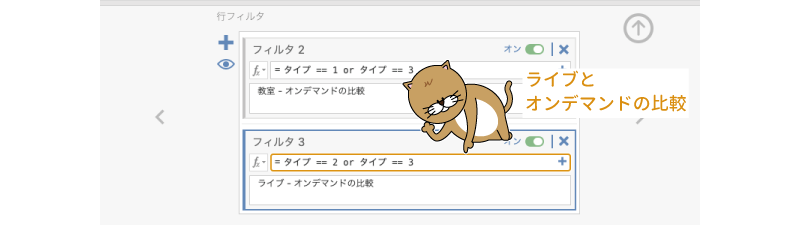
図6.95: 「ライブ」と「オンデマンド」の比較用フィルタ
3つのフィルタが完成したら,そのうちの1つのみを「オン」にして,残りは「オフ」にします。ここではまず,1つ目のフィルタのみを「オン」に,それ以外を「オフ」にしましょう(図6.96)。
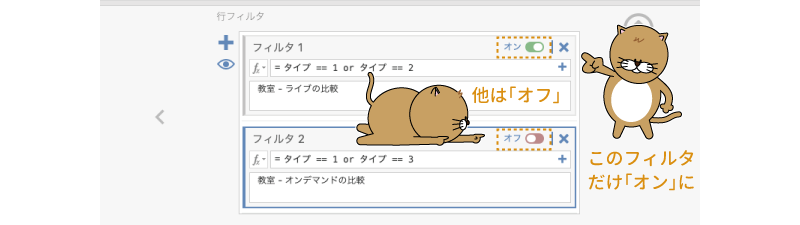
図6.96: 1つ目のフィルタだけを「オン」に設定
ここまでの設定が終わったら,フィルタの設定画面を閉じて,先ほどの「多変量共分散分析」の結果のうち,多変量の検定の部分を見てください。今,ここに表示されているのは授業のタイプが「教室」と「ライブ」の場合のデータのみを用いて行った多変量分散分析の結果です(図6.97)。
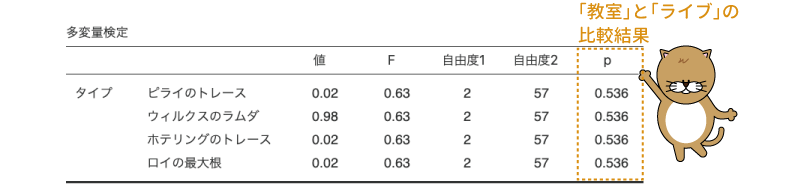
図6.97: 「教室」と「ライブ」の比較
この分析結果では,どの多変量統計量を用いた場合もFの値は同じになり,そして検定結果も同じになります。そして,この検定の有意確率はp=0.536ですので,この水準間では学生の評価の間に有意な差はないということになります。
今度は「教室」授業と「オンデマンド」授業で比較してみます。フィルタの設定で「フィルタ1」は「オフ」に,「フィルタ2」を「オン」にして,再度先ほどの結果を見てみると,今度は「教室」と「オンデマンド」のデータのみを用いた計算結果が表示されています(図6.98)。この結果から,「教室」と「オンデマンド」授業の間では有意確率はp=0.004であることがわかります。
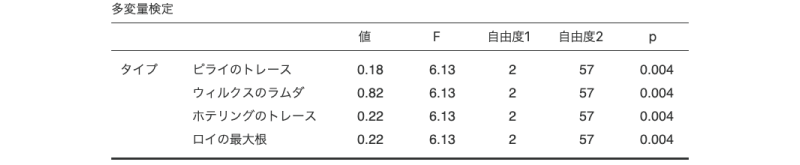
図6.98: 「教室」と「オンデマンド」の比較
なお,結果を慎重に判断するためには,ボンフェロニ法あるいはホルム法によって,この有意確率を修正したほうがよいでしょう。今回は全部で3回の多重比較を行うので,ボンフェロニ法であれば,このp=0.004を3倍して判断することになります。すると,p=0.004×3=0.012で,この水準間の差は有意ということになります。
最後に,「ライブ」と「オンデマンド」の比較です。「フィルタ3」を「オン」にして,それ以外は「オフ」にしましょう(図6.99)。
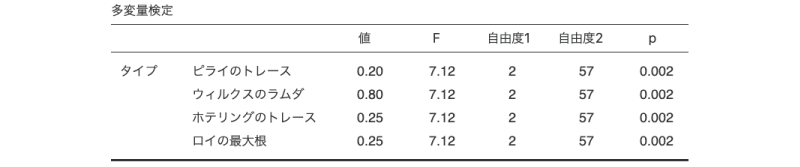
図6.99: 「ライブ」と「オンデマンド」の比較
この結果から,「ライブ」と「オンデマンド」の比較ではp=0.002です。このp値をボンフェロニ法で修正すると,p=0.002×3=0.006となり,この差についても結果は有意です。
これらの結果から,多変量での多重比較の結果,「教室」と「ライブ」の授業の間には有意な差は見られず,「オンデマンド」授業だけが他の2つと異なる傾向を持っているということがわかります。
行列は線形代数と呼ばれる数学領域で用いられるもので,関連のある複数の値を「行(各参加者など)」と「列(各変数など)」に並べてひとまとめにしたものです。線形代数では,この行列をを用いてさまざまな計算を行います。こうして複数の値をひとまとめにすることによって複雑な計算を大幅に簡素化できるため,多変量解析において行列は不可欠といえるものです。ただ,その説明のためにはかなりのページが必要になるので,ここでは行列については詳しく触れません。詳しくは線形代数の教科書や参考書などを参照してください。↩︎
行数と列数が同じ行列において算出される,その行列における固有の値です。その行列を用いて空間座標の変換を行った場合に,変換後の空間が元の空間の何倍の大きさになるかを示す値というような形で説明されます。非常におおざっぱにいえば,その行列がもつ影響力の大きさのようなものです。↩︎
「固有値」というのは主成分分析や因子分析でも頻繁に出てくる言葉ですが,行列についてのある程度の知識がないと説明が難しい概念です。非常におおざっぱにいえば,行列式と同様に,この値もその行列がもつ影響力の大きさを表しているといえます。ただし,行列式とは異なり,固有値は列数と同じ個数だけ算出されます。↩︎