8.3 対応なし［χ²独立性検定］

ここからはクロス集計表（分割表）の分析についてみていきましょう。クロス集計表とは，行と列にそれぞれ異なる変数をとり，次のようにして複数の変数の値を組み合わせた形で集計をした表のことをいいます（表8.6）。

表8.6: 性別とサラダの好き嫌いについてのクロス集計表
サラダ
好き 嫌い 計
性別
男 70 30 100
女 90 10 100
計 160 40 200

このようなクロス集計表を用いた分析では，表の列に位置する変数と行に位置する変数が互いに「独立」であるかどうかを確かめる独立性検定がよく用いられます。2つの変数が「互いに独立」であるとは，お互に無関係であるということです。

たとえば，先ほどの表8.6はサラダの好き嫌いと性別（男女）のクロス集計表ですが，この表を見ると，サラダが嫌いという回答の比率は，女性よりも男性の方が高くなっています。この場合，サラダを嫌いと答えたのは男性で100人中30人，女性では100人中10人というように，性別によってサラダの好き嫌いに違いが見られるので，サラダの好き嫌いと性別には関連があるということになります。

これに対し，次の表8.7では，男性と女性でハンバーグを好きだと答えた人と嫌いだと答えた人の比率は同じです。この場合には，ハンバーグの好き嫌いが性別によって異なるということはなく，ハンバーグの好き嫌いと性別は無関係（独立）であるといえます。

表8.7: 性別とハンバーグの好き嫌いについてのクロス集計表
ハンバーグ
好き 嫌い 計
性別
男 95 5 100
女 95 5 100
計 190 10 200

8.3.1 考え方

ここでは，次の例を用いて独立性検定の考え方を見ていきましょう。

成人男女各100人を対象に，「ショートケーキ」，「チーズケーキ」，「チョコレートケーキ」の中でどれが一番好きかを選んでもらいました。その結果をまとめたものがこのサンプルデータ（frequencies_data03.omv）です（図8.18）。

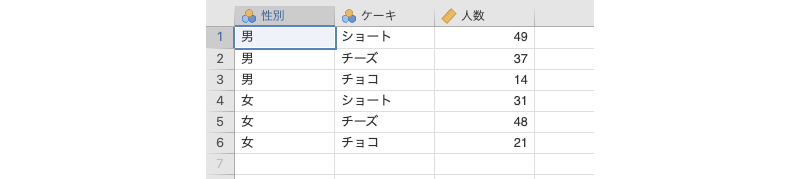
サンプルデータ

図8.18: サンプルデータ

  • 性別　性別（男，女）
  • ケーキ　ケーキの種類
    • ショートケーキ：ショート
    • チーズケーキ：チーズ
    • チョコレートケーキ：チョコ
  • 人数　そのケーキを選んだ人数

この結果から，好きなケーキに男女で違いがあるといえるかどうか（独立でないといえるかどうか）を見たいとします。

まず，サンプルデータを選択したケーキと性別のクロス集計表の形にすると表8.8のようになります。

表8.8: 性別とケーキの選択についてのクロス集計表
ケーキの種類
ショートケーキ チーズケーキ チョコレートケーキ 計
性別
男 49 37 14 100
女 31 48 21 100
計 80 85 35 200

さて，この結果から，ケーキの好み（どのケーキを選択したか）に男女による違いがあるかどうかをみるにはどうすればよいのでしょうか。統計的仮説検定の常として，そのような場合には，まず男女による違いが「ない」場合にどのようになるかを考えます。

ケーキの好みに男女による違いがない場合というのは，男性も女性も各ケーキの選択率が同じということです。もしそうだったとすると，男女ともに全体におけるケーキの選択率と同じ比率でそれぞれのケーキが選択されるはずです。つまり，表8.9のような人数配分になるはずです。

表8.9: 性別とケーキの選択の期待度数
ケーキの種類
ショートケーキ チーズケーキ チョコレートケーキ 計
性別
男 40 42.5 17.5 100
女 40 42.5 17.5 100
計 80 85.0 35.0 200

そしてこれが，ケーキの選択と性別が独立（無関係）である場合の「期待度数」ということになります。

ここから先は，カイ2乗適合度検定の場合と考え方は同じです。この期待度数と，実際の観測データ（観測度数）の間で差を求め，その差の大きさを1つの値にまとめたうえで，そのようなずれの生じる確率がどの程度であるかを算出します。

この場合の帰無仮説は「ケーキの選択と性別は独立である」で，検定結果が有意であった場合には，「ケーキの選択と性別には関連がある（独立でない）」ということになります。

8.3.2 分析手順

独立性検定を実施するには，分析タブの「inline 度数分析」で「クロス集計表」のところにある「対応なし［\(\chi^2\)独立性検定］」を選択します（図8.19）。

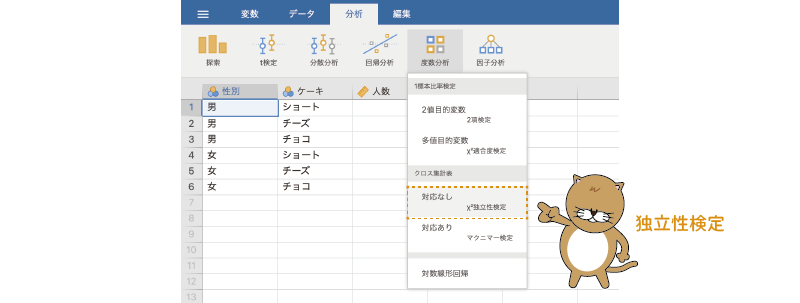
独立性検定の実行

図8.19: 独立性検定の実行

すると，図8.20のような画面が表示されます。

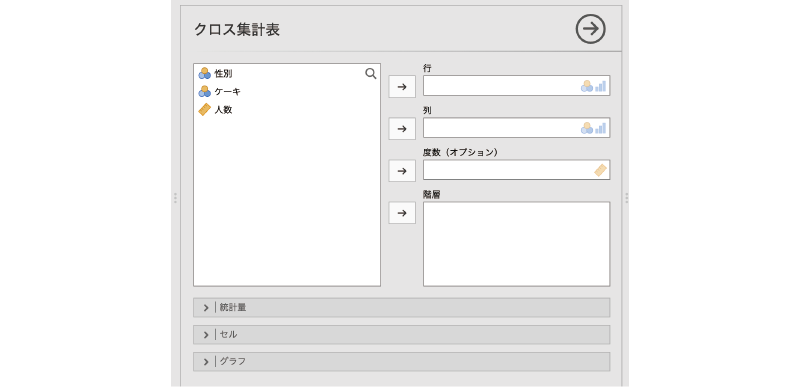
独立性検定の設定画面

図8.20: 独立性検定の設定画面

  • 行　クロス集計表の行に配置する変数を指定します。
  • 列　クロス集計表の列に配置する変数を指定します。
  • 度数（オプション）　度数が含まれている変数を指定します（オプション）
  • 階層　クロス集計表を分割する変数を指定します。
  • | 統計量　統計量に関する設定を行います。
  • | セル　クロス集計表の各セルに関する設定を行います。
  • | グラフ　結果をグラフに示します。

たくさんの設定項目があるのですが，基本的な分析はそれらを使用しなくても可能です。

分析では，クロス集計表の行と列に配置する変数を指定します。今回は，行に「性別」を，列に「ケーキ」を配置することにしましょう。

また，今回のデータもこれまでと同様に度数を集計済みのものですので，度数が入った変数（「人数」）を「度数（オプション）」のところに指定します。各個人の回答が1行ずつ入力されているデータの場合，この部分の設定は不要です。

設定後の画面は図8.21のようになります。これで基本の分析設定は終了です。

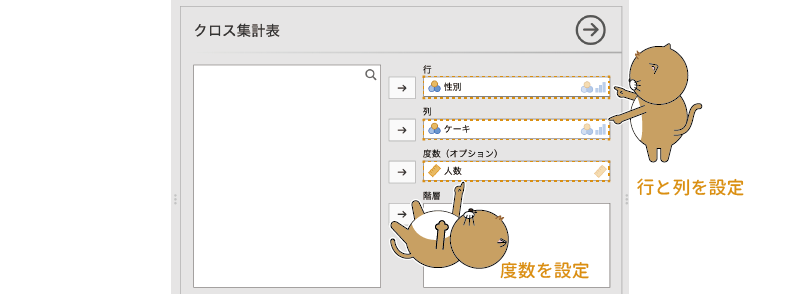
分析する変数を設定

図8.21: 分析する変数を設定

8.3.3 分析結果

それでは結果を見てみましょう。分析結果は図8.22のような形で得られます。

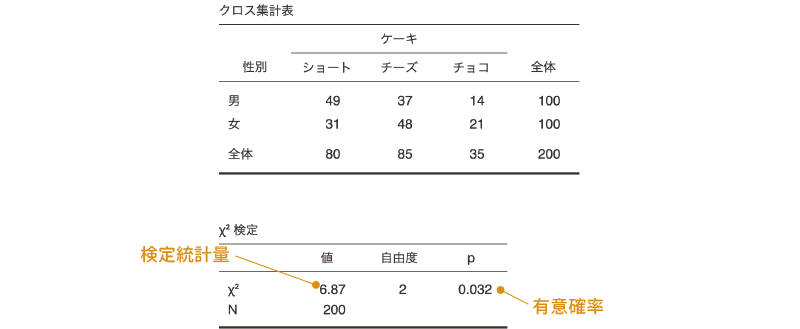
独立性検定の分析結果

図8.22: 独立性検定の分析結果

1つ目の表は，観測データについての度数分布表です。行と列が正しく設定されているか確認しましょう。また，集計済みのデータではなく，1人1人の回答が入力されているデータで分析を行う場合には，この度数分布表でそれぞれの度数をよく確認しておきましょう。

その下の2つ目の表が独立性検定の結果です。独立性検定の結果の表には，適合度検定の場合と同じで検定統計量（\(\chi^2\)）と自由度，そして有意確率（p）の値が示されています。また，独立性検定の場合には，総度数（N）についても示されています。この表のpの値が有意水準を下回る場合に，このデータの母集団の比率が想定される比率と有意に異なると判断します。

今回の分析結果ではp = 0.032ですので，ケーキの選択と性別には関連がある（独立でない）ということになります。

8.3.4 層別分析

ここで，もう1つ別のデータをみてみましょう。次のサンプルデータ（frequencies_data04.omv）を開いてください。このデータは先ほどのデータとよく似ていますが，これは先ほどのデータに子供を対象に調査した結果を加えたものになっています（図8.23）。

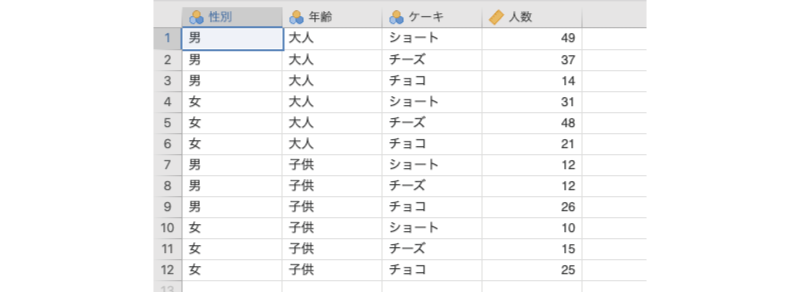
サンプルデータ

図8.23: サンプルデータ

  • 性別　性別（男，女）
  • 年齢　年齢（大人，子供）
  • ケーキ　ケーキの種類
    • ショートケーキ：ショート
    • チーズケーキ：チーズ
    • チョコレートケーキ：チョコ
  • 人数　そのケーキを選んだ人数

先ほどと同様に，今回もケーキの選択と性別に関連があるか（独立でないか）について検討したいと思います。ただし，ここで気をつけなくてはならないのが，このデータには大人を対象とした調査結果と子供を対象とした調査結果が混在しているということです。大人と子供でケーキの好みに違いがなければ大人と子供のデータを一まとめにして分析してもよいでしょうが，大人と子供でケーキの好みに大きな違いがあるのであれば，正しい分析結果が得られない可能性が高くなります。

このようなデータの場合，ケーキの選択と性別の関連を適切に把握するために，分析対象のクロス集計表を大人と子供にグループ分けしたうえで分析するという方法がとられます。このようにしてクロス集計表を別のグループ変数で分割して分析する方法は，層別分析と呼ばれます。jamoviでは，この層別分析についても簡単に実行できるようになっています。

分析手順

層別分析を実施するためには，「inline 度数分析」から「対応なし［\(\chi^2\)独立性検定］」を選択し，先ほどと同様に「行」に「性別」，「列」に「ケーキ」，そして「度数（オプション）」に「人数」を指定します。

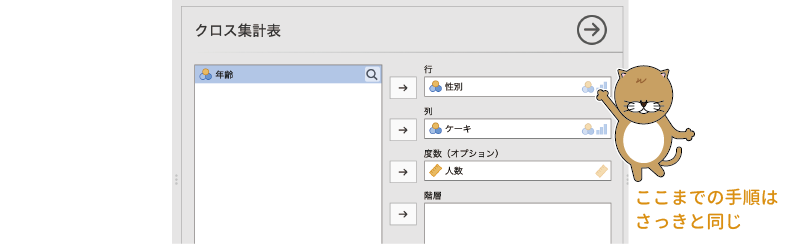
層別分析の設定（その1）

図8.24: 層別分析の設定（その1）

なお，「度数（オプション）」の設定は，各個人の回答が1行ずつ入力されているデータの場合には不要です。

そしてそのうえで，グループ変数である「年齢」を，設定画面の「階層」に設定します。

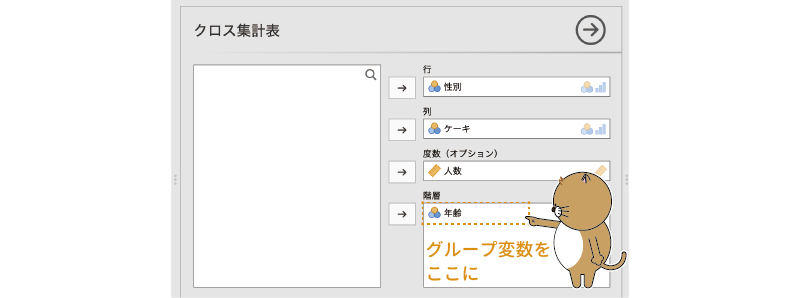
層別分析の設定（その2）

図8.25: 層別分析の設定（その2）

層別分析の設定はこれで終わりです。結果を見てみましょう。

分析結果

分析の設定画面でグループ変数を「階層」に設定すると，分析結果は図8.26のような形になります。全体としての構成は大きく変わりませんが，度数分布表と独立性検定の結果には，データ全体での結果と，大人と子供というグループごとの結果（層別の分析結果）の両方が含まれています。

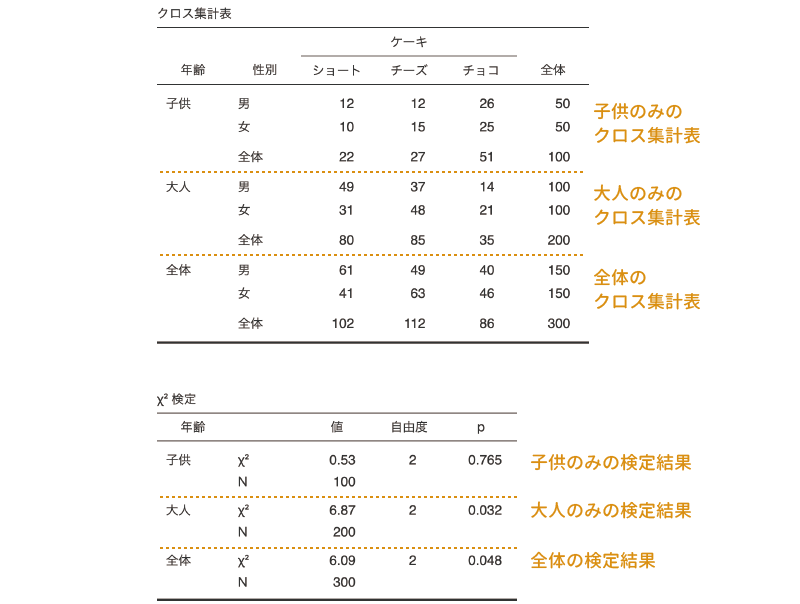
層別分析の結果

図8.26: 層別分析の結果

この結果を見ると，大人ではケーキの選択と性別に有意な関連が見られますが，子供では有意な関連は見られません。つまり，大人か子供かによって，ケーキの選択の仕方と性別の関連は異なるということになります。

なお，全体での結果はp = 0.048で有意ですが，このデータでは大人は男女各100人であるのに対し，子供は男女各50人ですので，データ全体においては子供よりも大人の結果の影響が強く反映されているためと考えられます。したがって，この場合には全体の検定結果はあまり意味がありません。

8.3.5 統計量

ここからは分析設定の詳細について見ていきましょう。| 統計量を展開すると，次の項目が表示されます（図8.27）。

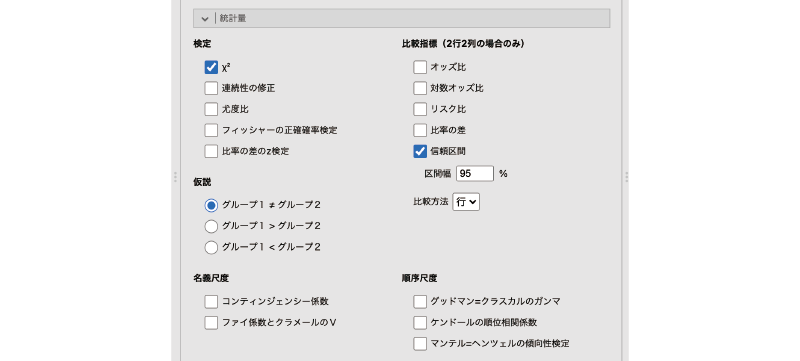
統計量の設定

図8.27: 統計量の設定

  • 検定　検定統計量に関する設定を行います。
  • 仮説　対立仮説に関する設定を行います。
  • 比較指標（2行2列の場合のみ）
  • 名義尺度　名義尺度の関連についての指標を設定します。
  • 順序尺度　順序尺度の関連についての指標を設定します。

非常にたくさんの項目が含まれていますが，ただ項目が多いだけでなく，この中には2行2列のクロス集計表の場合のみ適用可能な項目や，層別分析の場合のみ適用可能な項目などがあり，少し複雑です。ここでは，これらを1つ1つ順番に見ていくことにしましょう。

検定

「検定」の部分では，クロス集計表の検定に用いる検定手法についての設定を行うことができます（図8.28）。

検定の設定項目

図8.28: 検定の設定項目

  • \(\chi^2\)　\(\chi^2\)統計量を算出します。
  • 連続性の修正　\(\chi^2\)値に対して連続性の修正を行います。
  • 尤度比　尤度比カイ2乗検定を行います。
  • フィッシャーの正確確率検定　フィッシャーの正確確率検定を行います。
  • 比率の差のz検定　比率の差に対してz検定を実施します。

一番最初の\(\chi^2\)については説明の必要はないと思いますので，2つ目以降の項目について簡単に見ていきます。

連続性の修正

独立性の検定や適合度検定に用いられる検定統計量は\(\chi^2\)と呼ばれますが，実際には\(\chi^2\)の近似値であって，\(\chi^2\)の値そのものではありません。そのため，クロス集計表の特徴によっては，この近似の程度が低くなる場合があるのです。そしてそのような場合に，算出した検定統計量を\(\chi^2\)分布にできるだけ近づけるように，イェーツの修正，あるいはイェーツの連続性の修正と呼ばれる修正を加えることがあります。このイェーツの修正は，一般にはクロス集計表が2行2列である場合，標本サイズが小さく，クロス集計表に期待度数が5未満のセルが1つ以上ある場合に用いられます。

この「連続性の修正」の項目にチェックを入れると，イェーツの修正を行った後の\(\chi^2\)の値が算出されます（図8.29）。

連続性の修正

図8.29: 連続性の修正

この結果は大人のみのデータを使ったクロス集計表の分析結果に連続性の修正を適用したものですが，このデータでは連続性の修正をしてもしなくても同じ結果になっています。

なお，イェーツの修正については，値を「修正しすぎる」傾向があることが知られています。そのため，このような修正を行うべきかどうかについては専門家の間でも意見が分かれるところです。

尤度比

「カイ2乗検定」というのは，検定統計量として\(\chi^2\)を用いるものの総称です。そして，独立性の検定として一般に用いられるカイ2乗検定は，ピアソンのカイ2乗検定とも呼ばれます。このように呼ばれるということは，それ以外のカイ2乗検定があるということです。

そして，その1つが尤度比カイ2乗検定です。ピアソンのカイ2乗検定では，\(\chi^2\)の値は期待度数と観測度数の差の2乗を元に算出されますが，尤度比カイ2乗検定では，\(\chi^2\)の値を期待度数と観測度数の比を用いて算出します。ほとんどの場合，この尤度比カイ2乗検定の結果はピアソンのカイ2乗検定の結果とよく似たものになります。また，結果の見方はピアソンのカイ2乗検定の場合と同じです（図8.30）。

尤度比

図8.30: 尤度比

フィッシャーの正確確率検定

カイ2乗検定で算出される検定統計量は近似値であるため，標本サイズが小さいデータでは正確な結果が得られないといわれています。その場合，一般には正確確率検定と呼ばれる手法を用いて，今回の観測データと同じ結果になる確率がどの程度あるのかを直接的に計算して検定するという方法がとられます。その正確確率検定の中で，もっとも代表的なのがフィッシャーの正確確率検定，あるいはフィッシャーの直接確率検定と呼ばれる検定手法です。

この「フィッシャーの正確確率検定」にチェックを入れると，フィッシャーの正確確率検定による検定結果を表示することができます。なお，この方法では直接的に確率を計算するため，検定統計量は算出されません（図8.31）。そのため，結果の表にはpの値だけが表示されます。このpの値が有意水準を下回る場合に，2つの変数の間に関連がある（独立でない）と判断します。

フィッシャーの正確確率検定

図8.31: フィッシャーの正確確率検定

比率の差のz検定

この項目は，クロス集計表が2行2列の場合にのみ適用可能なオプションです。

独立性検定の最初のところで用いたハンバーグへの好みと性別のクロス集計表のように，クロス集計表の行と列に関連がなく，互いに独立である場合には，男女でハンバーグの好き・嫌いの比率は同じになり，また，ハンバーグの好き・嫌いで男女比は同じになります。ということは，このようにして行ごと，列ごとで見た比率が同じでなければ，行に置かれた変数と列に置かれた変数は独立でないということになります。

「比率の差のz検定」の項目では，このような考え方から，各行および各列で度数の比率が同じといえるかどうかの検定を行います。度数の比率が等しければ，それは行と列が互いに独立であるということを意味し，そうでなければ行と列には関連があるということを意味するわけです。

たとえば，男女各100人にイヌとネコのどちらが好きかをたずねた結果をまとめたクロス集計表があるとしましょう（表8.10）。

表8.10: 性別とイヌ派・ネコ派についてのクロス集計表
イヌ ネコ 計
性別
男 70 30 100
女 55 45 100
計 125 75 200

この表では，自分がイヌ派（ネコよりイヌが好き）と答えたのは男性では100人中70人（比率0.7），女性では100人中55人（比率0.55）ですので，男女の間でイヌ派の比率には0.15の差があります。この検定では，このようにして求めた比率の差を，全体におけるイヌ派の比率と男女それぞれの人数を用いてzに変換し，このzの値を用いて検定を行います。検定の結果が有意であった場合，2つの比率に差があるとみなします（図8.32）。

比率の差のz検定

図8.32: 比率の差のz検定

イヌ派・ネコ派のデータについて比率の差の検定を行ったところ，p = 0.028で検定結果は有意となりました。この結果から，男女でイヌ派・ネコ派の比率に有意な差があるということになります。

仮説

「仮説」では，「比率の差のz検定」における対立仮説を設定します（図8.27）。

仮説の設定項目

図8.33: 仮説の設定項目

  • グループ1 ≠ グループ2　グループ1と2で比率が異なるかどうかを検定します（両側検定）
  • グループ1 > グループ2　グループ1の比率がグループ2より大きいかどうかを検定します（片側検定）
  • グループ1 < グループ2　グループ1の比率がグループ2より小さいかどうかを検定します（片側検定）

この設定項目が結果に影響するのは，「比率の差のz検定」にチェックが入っている場合のみです。なお，片側検定を使用する際には，結果の「\(\chi^2\)検定」の表の下にある注釈で，比較の向きが正しいかどうかをよく確認してください。また，この「仮説」の右側にある「比較方法」の部分を「行」に設定すると行ごとの比率の差の検定，「列」にすると列ごとの比率の差の検定になります。

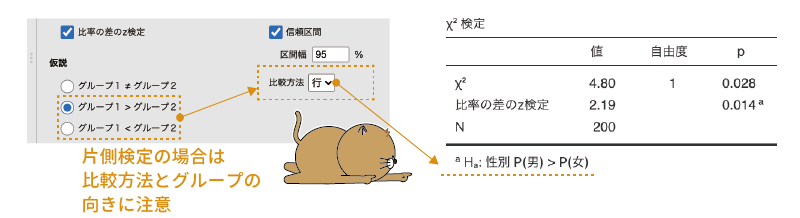
片側検定の場合は比較の向きに注意

図8.34: 片側検定の場合は比較の向きに注意

比較指標（2行2列の場合のみ）

ここに含まれている設定項目は，2行2列（2×2）のクロス集計表の場合のみ有効なものです。

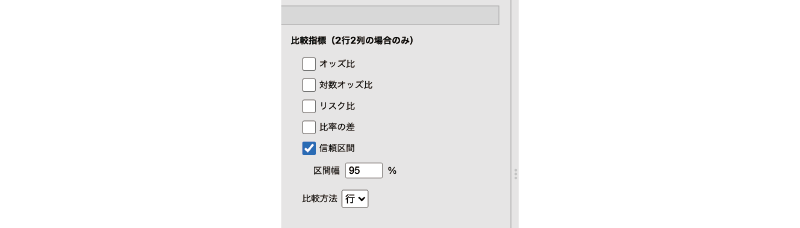
2行2列のクロス集計表における比較指標

図8.35: 2行2列のクロス集計表における比較指標

  • オッズ比
  • 対数オッズ比
  • リスク比
  • 比率の差
  • 信頼区間
  • 比較方法

ここでは，オッズや比率を2つのグループ間で比較する際に用いられる指標の設定を行いますが，その際，行での比較を行うか，列での比較を行うかは，各指標の下にある「比較方法」で設定します。

この「比較方法」を「行」に設定すると，オッズや比率が行ごとに算出され，それらの間で比較が行われます。先ほどのイヌ派とネコ派のクロス集計表でいうと，男性におけるイヌ派の比率と，女性におけるイヌ派の比率の間で比較が行われます（図8.36）。

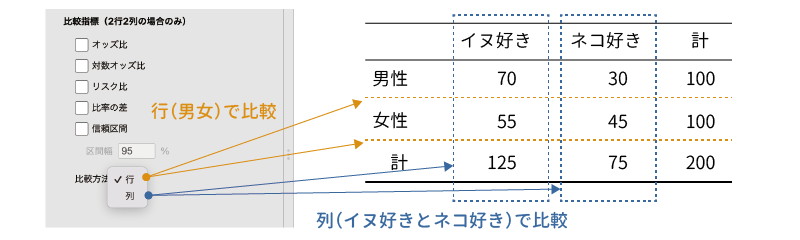
比較方法の設定

図8.36: 比較方法の設定

これに対して，「比較方法」を「列」に設定すると，ネコ派における男女比と，イヌ派における男女比の間での比較になります。この「比較方法」の設定は，「比率の差のz検定」にも反映されます。

では，ここで設定できる各種指標について簡単にみておきましょう。

オッズ比

「あり・なし」や「はい・いいえ」などの2値変数において，「あり」である確率と「なし」である確率の比をとったものをオッズと呼びます。先ほどの「イヌ派」と「ネコ派」の例でいえば，「イヌ派率」と「ネコ派率」を「イヌ派率/ネコ派率」の形で表したものが「イヌ派のオッズ」です。

そして，さらにそのオッズ2種類を比の形にして表したものがオッズ比です。先ほどの例では，男性ではイヌ派のオッズは「0.7/0.3 = 2.33」，女性ではイヌ派のオッズは「0.55/0.45 = 1.22」ですので，イヌ派についての男女のオッズ比は「2.33/1.22 = 1.91」となります。

対数オッズ比

2つの確率の比であるオッズは，2つの確率のうちの小さな値を基準（分母）におくか，大きな値を基準におくかで値のとりうる範囲が大きく異なります。たとえば，男性のイヌ派のオッズは「70/30 = 2.33」ですが，これは男性の場合，イヌ派である確率の方がネコ派である確率の2.33倍であることを意味します。このように小さい方の値を基準とした場合には，オッズは1から無限大までの範囲をとりうる値になります。

これに対し，男性のネコ派のオッズは「0.3/0.7 = 0.43」で，これはネコ派の確率がイヌ派の確率の0.43倍であるということになるのですが，このように大きい方の値を基準としてオッズを算出した場合，オッズの値は0から1までの範囲にしかなりません。

また，イヌ派のオッズとネコ派のオッズは，0.7/0.3と0.3/0.7というように分数の上下を入れ替えただけの違いであるのに，その値は2.33と0.43というようにまったく異なる数値になっていて，とくに関連があるようには見えません。

ところが，これらのオッズを対数変換すると，「log(0.7/0.3) = 0.85」，「log(0.3/0.7) = \(-\textsf{0.85}\)」となって，両者が方向を逆転させた関係にあることがわかりやすくなります。また，この場合には，プラスの値は0から無限大まで，マイナスの値もマイナス無限大の値をとることができるようになるのです。このように，オッズを用いる場合には，それを対数変換した方が関係を理解しやすくなることが多いのです。

これはオッズ比の場合も同様で，そしてオッズ比を対数に変換したものが対数オッズ比です。先ほどの例の，イヌ派についての男女のオッズ比を対数オッズ比に直すと，「log 1.91 = 0.65」になります。

リスク比

オッズ比が2グループのオッズの比であるのに対して，2グループの確率をそのまま比の形で表したものがリスク比です。先ほどのイヌ派・ネコ派の例でいうと，イヌ派の割合は男性では0.7（70%），女性では0.55（55％）ですので，「0.7/0.55 = 1.27」というのがイヌ派についての男女のリスク比ということになります。

比率の差

これは，2つのグループにおける比率の差です。「検定」の設定項目にある「比率の差のz検定」は，この2グループの比率の差をzに変換して検定を行っています。

イヌ派・ネコ派の例では，イヌ派の割合は男性で0.7，女性で0.55ですので，比率の差の値は「\(\textsf{0.7}-\textsf{0.55} = \textsf{0.15}\)」になります。

ここまでの指標の関係をまとめると図8.37のようになります。

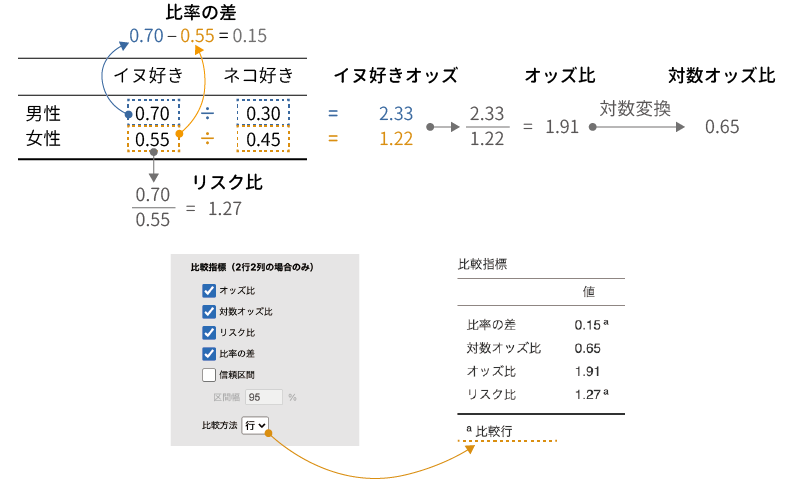
比較指標の関係と一覧

図8.37: 比較指標の関係と一覧

信頼区間

「信頼区間」の項目にチェックを入れると，オッズ比や対数オッズ比，リスク比などの各指標について，指定した幅の信頼区間が算出されます。

名義尺度

「名義尺度」では，分析対象のデータが名義型変数（inline）である場合の連関係数に関する設定を行います。連関係数とは，クロス集計表における行の要素と列の要素の間の関連の強さを表す指標のことです。

ここには，次の2つの設定項目が含まれています（図8.38）。

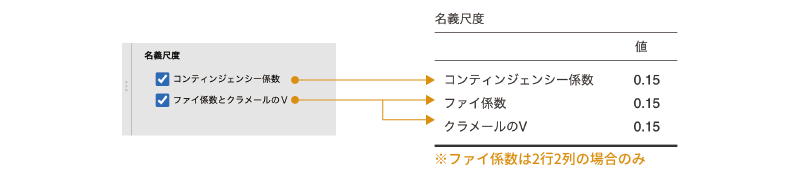
名義尺度の連関係数

図8.38: 名義尺度の連関係数

  • コンティンジェンシー係数
  • ファイ係数とクラメールのV
コンティンジェンシー係数

コンティンジェンシー係数は，\(\chi^2\)の値を「\(\chi^2\)+総度数」で割った値の平方根で，これはクロス集計表の行要素と列要素の関連の強さを示します。この値はピアソンの連関係数Cとも呼ばれます。この値は，行と列の連関が0である（行と列が独立である）場合に0となり，連関が強いほど1に近い値になります。

ファイ係数とクラメールのV

この項目にチェックを入れると，ファイ係数とクラメールの連関係数Vの2種類の値が算出されます。

ファイ（\(\varphi\)）係数と呼ばれるものには，\(\chi^2\)の値を総度数で割ったものの平方根として求められるものと，ピアソンの積率相関係数を2行2列のクロス集計表に適用したもの（これは四分点相関係数とも呼ばれます）の2種類が存在しますが，jamoviで算出されるのは後者です。このファイ係数は，2行2列のクロス集計表でのみ算出されます。

もう1つのクラメールの連関係数Vは，\(\chi^2\)の値を行数と列数の小さい方の値で割って平方根を求めたもので，こちらは2行2列よりも大きなサイズのクロス集計表に対しても算出されます。なお，2行2列のクロス集計表では，ファイ係数とクラメールのVは同じ値になります。

これらの値も，コンティンジェンシー係数と同様に，行と列の連関が0である（行と列が独立である）場合に0となり，連関が強いほど1に近い値になります。

順序尺度

「順序尺度」では，分析対象のデータが順序型変数（inline）である場合の関連度指標に関する設定を行います。

ここには，次の3つの項目が含まれています（図8.39）。

順序尺度の関連度

図8.39: 順序尺度の関連度

  • グッドマン=クラスカルのガンマ
  • ケンドールの順位相関係数
  • マンテル=ヘンツェルの傾向性検定
グッドマン=クラスカルのガンマ

グッドマン=クラスカルのガンマは，順位相関係数の一種です。2行2列のクロス集計表の場合には，このガンマの値はユールのQと呼ばれることもあります。グッドマン=クラスカルのガンマは，スピアマンの順位相関係数などと同様に\(-\textsf{1}\)から1までの範囲をとります。

この設定は，クロス集計表の行と列の両方が順序型変数である場合に有効です。それ以外の場合にも計算計算は表示されますが，それらの値は適切ではない可能性があります。

ケンドールの順位相関係数

この項目にチェックを入れると，ケンドールの順位相関係数が算出されます。

この設定は，クロス集計表の行と列の両方が順序型変数である場合に有効です。それ以外の場合にも計算計算は表示されますが，それらの値は適切ではない可能性があります。

マンテル=ヘンツェルの傾向性検定

マンテル=ヘンツェルの傾向性検定は，行数または列数が2で，もう一方が順序型変数である場合のクロス集計表に使用可能な検定です。

たとえば表8.11のようなクロス集計表があったとします。この表には，行方向にはある特徴のあり・なしが，列方向には学年が置かれています。このようなクロス集計表で，その特徴のあり・なしと学年の間に関連が見られるかどうかを確かめるのがマンテル=ヘンツェルの傾向性検定です。よく似た名前をもつ検定にコクラン=マンテル=ヘンツェル検定がありますが，これとは別物ですので注意してください。

表8.11: 特徴の有無と学年についてのクロス集計表
低学年 中学年 高学年 計
特徴
あり 10 20 40 70
なし 90 80 60 230
計 100 100 100 300

この検定では，順序型変数（低学年・中学年・高学年）を「1，2，3」という数値に置き換え，名義型変数（あり・なし）を「1，2」に置き換えて，2つの変数の間のピアソンの積率相関係数を算出します。そしてその相関係数の2乗値に「総度数−1」をかけた値が\(\chi^2\)として算出されます。この検定の結果，有意確率pの値が有意水準を下回る場合に，2つの変数の間に関連があると判断します。

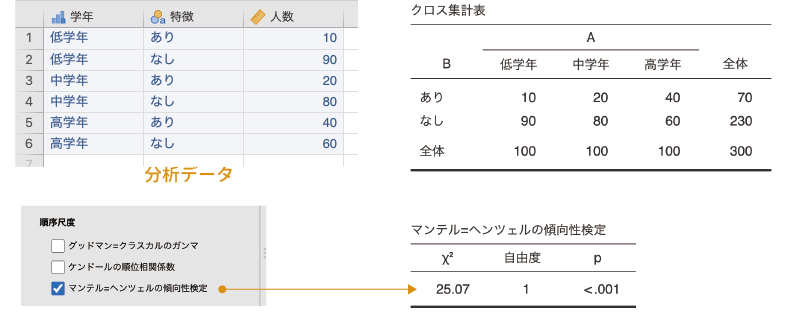
マンテル=ヘンツェルの傾向検定

図8.40: マンテル=ヘンツェルの傾向検定

8.3.6 セル

ここでは，クロス集計表のセル（1つ1つのマス目）に表示する値についての設定を行います（図8.41）。

セルの設定

図8.41: セルの設定

  • 度数
    • 観測度数　観測度数を表示します。
    • 期待度数　期待度数を表示します。
  • パーセント
    • 行　それぞれの行における各セルのパーセントを示します。
    • 列　それぞれの列における各セルのパーセントを示します。
    • 全体　各セルの度数が総度数に占めるパーセントを示します。

「度数」にある「観測度数」と「期待度数」は，それぞれ観測度数と期待度数を表示に関する設定項目です。これらの項目にチェックを入れると，チェックした項目の値がクロス集計表に表示されます（図8.42）。

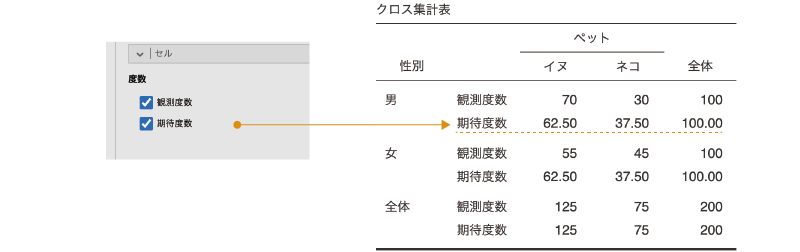
期待度数の表示

図8.42: 期待度数の表示

また，「パーセント」にある設定項目は，各セルのパーセント値の表示・非表示についての設定です。「行」にチェックを入れると，それぞれの行ごとに各列の値の占める割合がその行の度数の何%であるかが表示されます。同様に，「列」にチェックを入れると，それぞれの列ごとに各行の値がその列に占める割合が何%であるかが表示されます（図8.43）。

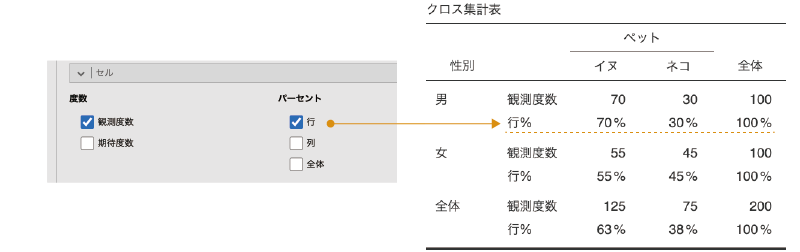
パーセントの表示

図8.43: パーセントの表示

「全体」も同様で，この項目にチェックを入れると各セルの度数が総度数の何%を占めるかがクロス集計表に表示されます。

8.3.7 グラフ

ここでは，クロス集計表の値を用いたグラフの作成に関する設定を行います（図8.44）。

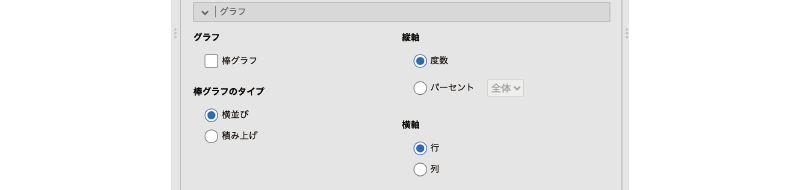
グラフの設定

図8.44: グラフの設定

  • グラフ
    • 棒グラフ　棒グラフを作成します。
  • 棒グラフのタイプ
    • 横並び　グループ別に，棒を横並びにして表示します。
    • 積み上げ　各グループの度数を縦に積み上げて表示します。
  • 縦軸
    • 度数　グラフの縦軸に度数を示します。
    • パーセント　グラフの縦軸に度数のパーセントを示します。
  • 横軸
    • 行　クロス集計表の行にある変数の値を横軸に配置します。
    • 列　クロス集計表の列にある変数の値を横軸に配置します。

ここの「グラフ」にある「棒グラフ」にチェックを入れると，クロス集計表の値を棒グラフとして示すことができます（図8.45）。

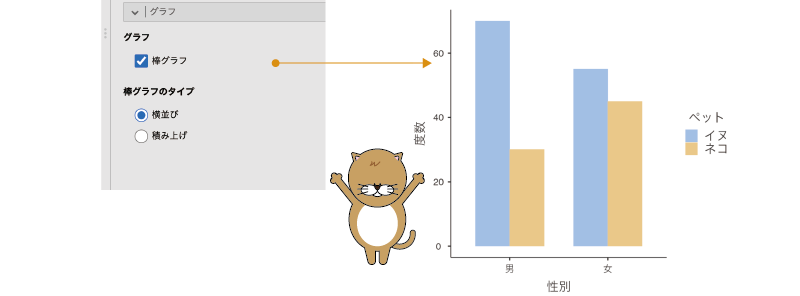
棒グラフの表示

図8.45: 棒グラフの表示

ここで作成できる棒グラフは，グループ別に値を横に並べて表示するスタイルと，それぞれのグループの度数を縦に積み上げて表示するスタイルの2種類のスタイルを選択することができます。「棒グラフのタイプ」で「横並び」を選択すると，異なるグループの度数が横並びの形で棒グラフに表示されます。これに対し，「積み上げ」を選択すると，異なるグループの度数が縦に積み上げられる形の棒グラフ（積み上げ棒グラフ）が表示されます（図8.46）。

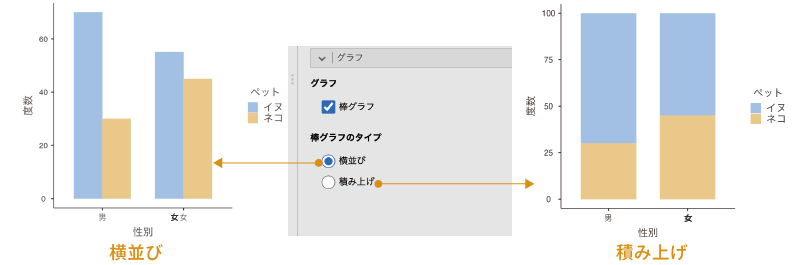
棒グラフのスタイル

図8.46: 棒グラフのスタイル

「縦軸」に含まれているのは，グラフの縦軸（数値軸）に示す値についての設定項目です。ここで「度数」を選択すると，グラフの縦軸には度数が示されます。これに対し，「パーセント」を選択した場合には，グラフの縦軸にはその度数が全体または行・列に占めるパーセントの値が縦軸に示されます（図8.47）。

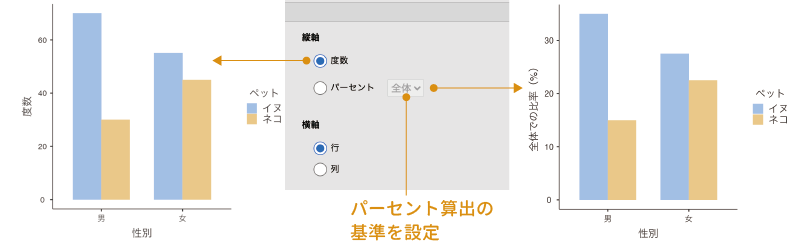
グラフの縦軸の設定

図8.47: グラフの縦軸の設定

また，全体，行，列のいずれに対するパーセント値を表示させるかは，「パーセント」の横のプルダウンメニューから選択して設定します。ここが「全体」になっている場合には全体におけるパーセント，「行」になっている場合には各行におけるパーセント，「列」になっている場合には各列におけるパーセントになります。

「横軸」に含まれているのは，グラフの横軸（項目軸）に用いる値についての設定項目です。ここで「行」を選択すると，グラフの横軸にはクロス集計表の行にある変数の値が用いられます。これに対し，「列」を選択した場合には，グラフの横軸にはクロス集計表の列にある変数の値が用いられます（図8.48）。

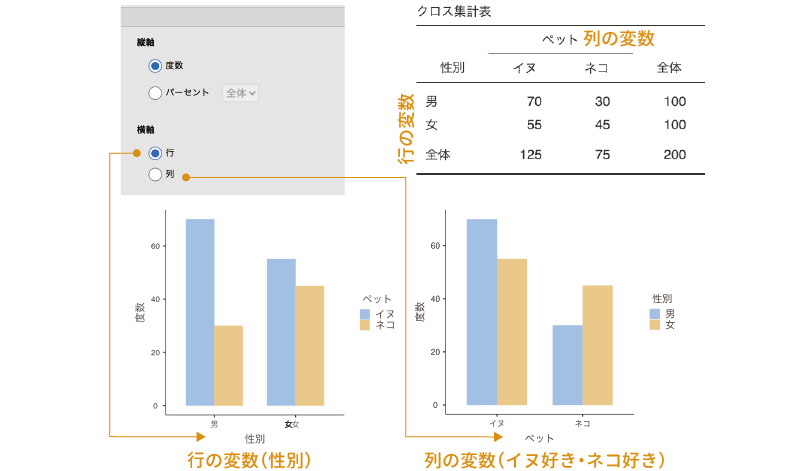
グラフの横軸の設定

図8.48: グラフの横軸の設定