6.6 1要因分散分析［クラスカル=ウォリス］

ここからはノンパラメトリックな分析について見ていきましょう。分散分析はt検定と同様にデータが正規分布であることが前提となるため，正規分布からかけ離れたデータには適用できません。その場合に用いられる方法の1つがノンパラメトリック検定ですが，ノンパラメトリック検定にも分散分析に相当する分析手法があります。

そのうち，繰り返しなしの1要因分散分析に相当するのがクラスカル=ウォリス検定です。

6.6.1 考え方

ここでは，1要因分散分析で用いたのと同じデータ（anova_data01.omv）を用いてクラスカル=ウォリス検定の考え方について見ていくことにしましょう（図6.100）。

サンプルデータ

図6.100: サンプルデータ

  • ID　実験参加者のID
  • 条件　文字条件（なし，不一致，一致）
  • 得点　課題の成績（0〜50点）

クラスカル=ウォリス検定の考え方は1要因分散分析とよく似ており，主効果（「条件」の違い）によるばらつきの大きさを，基準となるばらつきの大きさと比較する形で検定を行います。ただし，主効果のばらつきや基準となるばらつきの大きさを，測定値の「順位」をもとに算出する点が異なります。

1要因分散分析では，各条件の平均値と全体平均値の差の2乗和を主効果の2乗和として求め，ここから主効果の分散（2乗平均）を算出しました。クラスカル=ウォリス検定では，各条件に含まれる測定値の順位の平均値と全体の順位平均値の差の2乗和を主効果の2乗和として算出します。

今回のデータを例に考えてみましょう。このデータには，各条件に25人分の測定値が含まれていますので，これらの測定値に小さい順に順位をつけると，その値は1から75の範囲になります11。すると，このデータ全体での順位の平均値は，1から75までの数値の合計を75で割って38と求まります。これが，1要因分散分析におけるデータ全体の平均値に相当します。

そして，このデータ全体における各測定値の順位を3つの条件それぞれで求めると，「なし」条件では34.38，「不一致」条件では25.14，「一致」条件では54.48というように，各条件の順位の平均値にばらつきがあるのがわかります。この各条件の平均値と，先ほどのデータ全体の順位平均値の差の2乗和が，クラスカル＝ウォリス検定における主効果の2乗和になるのです。

なお，1要因分散分析では，主効果（条件の違い）で説明しきれない部分（残差）を基準にして主効果が有意といえるかどうかを判断しますが，クラスカル=ウォリス検定では，全体の順位平均値と各測定値の順位の差の2乗和を基準にして判断を行います。このように，クラスカル=ウォリス検定では，とにかく各測定値の「順位」の情報を利用しながら，条件間に差があるといえるかどうかを判断していくのです。

6.6.2 分析手順

では早速，分析してみましょう。クラスカル=ウォリス検定の実行には，分析タブの「inline 分散分析」で，「ノンパラメトリック」の下にある「1要因分散分析［クラスカル=ウォリス］」を選択します。分析メニューに「1要因分散分析」とあるのは，この分析が1要因分散分析のノンパラメトリック版に相当するものだからです図6.101。

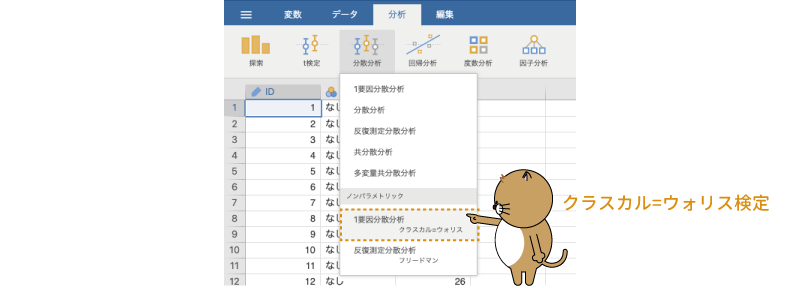
クラスカル=ウォリス検定の実行

図6.101: クラスカル=ウォリス検定の実行

すると，図6.102のようなシンプルな画面が表示されます。

クラスカル=ウォリス検定の設定画面

図6.102: クラスカル=ウォリス検定の設定画面

この画面で，「得点」を「従属変数」に，「条件」を「グループ変数」に指定すれば，これで分析終了です（図6.103）。

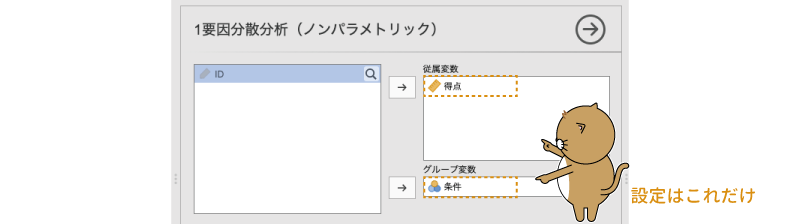
クラスカル=ウォリス検定の分析設定

図6.103: クラスカル=ウォリス検定の分析設定

6.6.3 分析結果

それでは結果を見てみましょう。クラスカル=ウォリス検定の結果は図6.104のような形で表示されます。

クラスカル=ウォリス検定の結果

図6.104: クラスカル=ウォリス検定の結果

クラスカル=ウォリス検定では，検定統計量として\(\chi^2\)（カイ2乗）の近似値が算出されるため，結果の表には\(\chi^2\)の値と自由度，そして有意確率が示されています。この検定の帰無仮説は「すべての条件で分布が同じ」であるため，この検定結果におけるpの値が有意水準を下回る場合に，条件間で分布が異なる（差がある）ということになります。そして今回の分析では，検定結果は有意でした。つまり，実験条件によって得点が異なるということです。

6.6.4 効果量と多重比較

クラスカル＝ウォリス検定では，基本の分析以外の設定項目は効果量と多重比較の2つだけです。

効果量

まず効果量についてですが，設定画面の「効果量」にチェックを入れると，図6.105のように結果の表の右端に効果量\(\varepsilon^2\)（イプシロン2乗）の値が表示されます。

クラスカル=ウォリス検定の効果量

図6.105: クラスカル=ウォリス検定の効果量

この\(\varepsilon^2\)の値は，各条件の順位の差の2乗和（主効果の2乗和）の値を全体の2乗和で割ったもので，1要因分散分析の場合の\(\eta^2\)（イータ2乗）と同じ考え方で算出される値です。そして，この\(\varepsilon^2\)の大きさの目安は，\(\eta^2\)の場合と同様です（表6.5）。ですので，今回の分析結果から，条件の違いによる主効果はかなり大きなものだといえます。

表6.5: \(\varepsilon^2\)の解釈の目安
\(\varepsilon^2\)の値 効果の大きさ
0.14 大
0.06 中
0.01 小
多重比較（DSCF）

設定画面の「多重比較（DSCF）」にチェックを入れると，すべての条件間での多重比較の結果が表示されます（図6.106）。

ノンパラメトリックな多重比較

図6.106: ノンパラメトリックな多重比較

その際に使用される検定方法はDSCF法（ドゥワス=スティール=クリッチロウ=フリグナー法）と呼ばれるもので，これはテューキー法による多重比較のノンパラメトリック版です。クラスカル＝ウォリス検定と同じく，この方法でも測定値の順位に基づく検定が行われます。また，この方法では，テューキー法による多重比較の場合と同様に調整済みの検定統計量が算出されますので，結果のp値を調整する必要はありません。

図6.106の結果の表にはWという値が示されていますが，これがこの検定の検定統計量です。そしてこの多重比較の結果から，「なし」条件と「一致」条件，「不一致」条件と「一致」条件の間に有意な差があることがわかります。

  1. 同順位（タイ）のものが含まれている場合は話が少し複雑になるので，ここでは同順位の測定値は考えないことにします。↩︎