6.3 反復測定分散分析
ここまでに見てきた分析例は,いずれも「対応なし」の場合のものでした。t検定と同様に,分散分析の場合にも対応なしの場合と対応ありの場合の分析方法があります。分散分析においては,対応ありのデータは「反復測定データ」や「繰り返しありのデータ」と呼ばれることが多いようです。
ところで,t検定では対応ありの方が対応なしの場合よりも単純でしたが,分散分析ではそうではありません。t検定の場合には比較する条件は2つだけですから,その2つの条件の測定値がそれぞれ別の対象者から得られたもの(対応なし)か,同じ対象者から得られたものか(対応あり)というような区別だけで済むでしょう。
しかし,分散分析の場合には,比較する条件(水準)が3つ以上である場合があります。その場合,前半5分,中盤5分,後半5分というように繰り返しの順序に意味があるような場合(時系列データ)と,単に3つの異なる条件(順不同)を同一参加者に対して実施した場合とでは「繰り返し」の意味が異なります。
また,2要因以上の分散分析では,分析に用いるすべての要因が繰り返しありの要因である場合と,そのうちの一部のみが繰り返しありの要因である場合とがあり得ます。このように,繰り返しあり(対応あり)のデータに対する分散分析は,「対応あり」と一言で済ませられないほどにさまざまなタイプのデータを扱うことになり,対応ありt検定の場合よりもずっと分析が複雑になるのです。
繰り返しありのデータ(反復測定データ)の分析方法は1つではなく,いくつかの方法があるのですが,jamoviには標準で「反復測定分散分析」という分析ツールが用意されていますので,ここではこの分析ツールを用いた場合の分析方法について見ていくことにします5。
6.3.1 考え方
先ほども説明したように,分散分析が扱う「繰り返しあり」データには非常にさまざまなタイプのものがありますので,それらのすべてについて説明しようとすると,それだけでも1冊の本になってしまうほどです。ですので,ここでは比較的シンプルな次のデータ(anova_data03.omv)の場合について考えることにしましょう(図6.48)6。
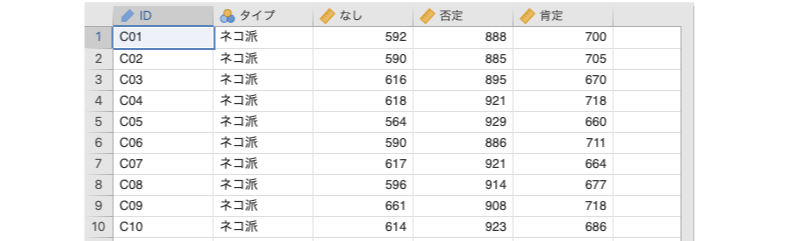
図6.48: サンプルデータ
ID実験参加者のIDタイプ参加者のタイプ(ネコ派,イヌ派)なし評価語を呈示しない場合の反応時間(単位:ms)否定「ネコ」と否定語をセットで呈示した場合の反応時間(単位:ms)肯定「ネコ」と肯定語をセットで呈示した場合の反応時間(単位:ms)
これは,ネコ派(ネコが大好きでイヌは好きでない)とイヌ派(イヌが大好きでネコは好きでない)各30名の参加者を対象に行った実験のデータです。この実験では,画面の中央にイヌまたはネコの画像を,画面上部の左右に「ネコ」や「イヌ」などの文字を呈示して,画像と一致するほうの文字を選択してもらうという課題を行いました。この際,「ネコ」と「イヌ」の左右の位置は試行ごとにランダムとしました。
実験条件としては,画面に「ネコ・イヌ」という反応語を呈示する際に「かわいい・ぶさいく」,「よい・わるい」,「ふわふわ・ごわごわ」など,よい印象を含む語と悪い印象を含む語(評価語)をセットにする場合と,「ネコ・イヌ」の反応語のみを呈示する場合を用いました。また,反応語と評価語をセットにする条件では,「ネコ」と「ごわごわ」などの否定的な印象の評価語をセットにした場合(否定条件)と,「ネコ」と「ふわふわ」などの肯定的な印象の評価語をセットにした場合(肯定条件)で測定を行いました(図6.49)。
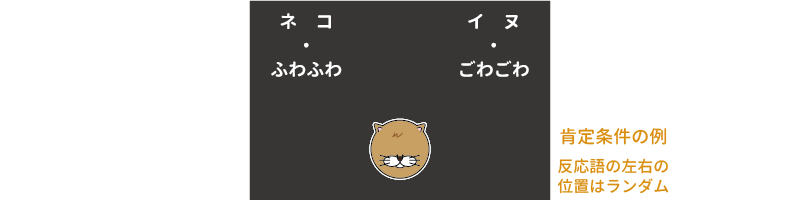
図6.49: 実験における刺激呈示の例
また,この実験では1人の参加者について,評価語なしの条件(なし条件)と肯定条件,否定条件の3つの条件すべてを実施し,これら3つの条件は順序をランダムにして複数回繰り返しました。データファイルに入力されている各参加者の測定値は,それぞれの条件における複数回の測定における反応時間の平均値をミリ秒(ms)で記録したものです。
実験についての説明が長くなりましたが,このデータから参加者のタイプ(ネコ派・イヌ派)によって各実験条件における反応時間に違いが見られるかどうかを知りたいとしましょう。この場合,ネコ派の参加者とイヌ派の参加者はそれぞれ別の人々で構成されていますので,参加者の「タイプ」の要因は繰り返しなし(対応なし)ということになりますが,各評価語条件(なし・否定・肯定)については1人の参加者で繰り返し測定を行っているので,これは繰り返しあり(対応あり)の要因です。
繰り返しのあり・なしは,データファイルではそれらが同じ行に入力されているか,それとも別の行に入力されているかという形で区別されます。繰り返し要因の測定値は,このサンプルデータファイルのように1人分の測定値が1行に入力された形になっている必要がありますので,その点は注意してください。このように,1人分のデータを1行に横並びに入力した形式のデータのことをとくにワイド形式のデータと呼ぶことがあります。
これに対し,1人分のデータを条件ごとに複数行に分けて入力されたデータはロング形式と呼ばれます。残念ながら,jamoviにはロング形式をワイド形式に変換する機能はありませんので,データがワイド形式になっていない場合には,ExcelやRなど,他のソフトで変換してから分析する必要があります。
さて,今回のデータでは,すべての参加者が評価語の3つの水準(なし・否定・肯定)すべてについて測定値を持っているため,この評価語の主効果を考える際には,各水準の平均値だけでなく,各参加者における3水準の平均値を求めることもできます。説明のために,今回のデータの最初の3行だけを使って表を作成すると表6.4のようになります。
| なし | 否定 | 肯定 | 平均値 | |
|---|---|---|---|---|
| 参加者1 | 592.0 | 888.0 | 700.0 | 726.7 |
| 参加者2 | 590.0 | 885.0 | 705.0 | 726.7 |
| 参加者3 | 616.0 | 895.0 | 670.0 | 727.0 |
| 平均値 | 599.3 | 889.3 | 691.7 | 726.8 |
この「各参加者における3水準の平均値」というのが重要な部分です。このようにして評価語3水準の平均値と参加者ごとの平均値を算出できるのであれば,「評価語」間,「参加者」間での平均値のばらつきを求めることもできるようになります。すると,これを「評価語」と「参加者」の2要因分散分析とみなして,ここから「評価語×参加者」の交互作用を算出できるのです。そしてこの「評価語×参加者」の交互作用は,評価語の影響(つまり評価語の主効果)が各参加者で異なる程度(個人差)を数値化したものです。つまりこれは,「評価語の主効果」における「個人差」の大きさを表します。
すると,評価語の主効果の検定では,主効果による平均値のばらつきと,この主効果の個人差によるばらつきの値が得られることになります。そして主効果の大きさと,その個人差の大きさがわかるのであれば,主効果の検定においては,「主効果の個人差」を誤差とみなす形で主効果の大きさを評価できるようになるというわけです。
これと同じことが参加者の「タイプ(ネコ派・イヌ派)×評価語」の交互作用においてもあてはまります。参加者ごとに交互作用の大きさを求めることができれば,その交互作用の個人差を算出することが可能になります。すると,交互作用の検定では,その交互作用の個人差を誤差とみなして交互作用の大きさを評価することができるのです。
6.3.2 分析手順
それでは分析手順を見てみましょう。分析の実行には,分析タブの「 分散分析」から「反復測定分散分析」を選択します(図6.50)。
図6.50: 反復測定分散分析の実行
すると,図6.51のようにたくさんの項目が含まれた設定画面が表示されます。
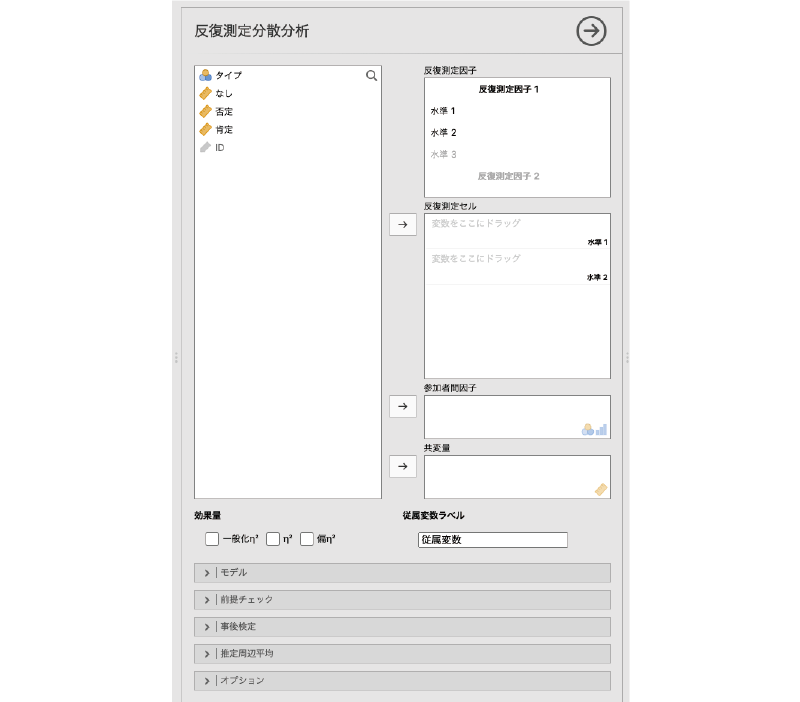
図6.51: 反復測定分散分析の設定画面
ここではまず,分析の基本設定について見ていきましょう。反復測定分散分析では,繰り返しのある要因とそうでない要因の区別が重要です。設定画面右側の一番上にある「反復測定要因」には,繰り返しありの要因がいくつあり,そしてそれぞれの要因の中に水準がいくつ含まれているかを指定します(図6.52)。
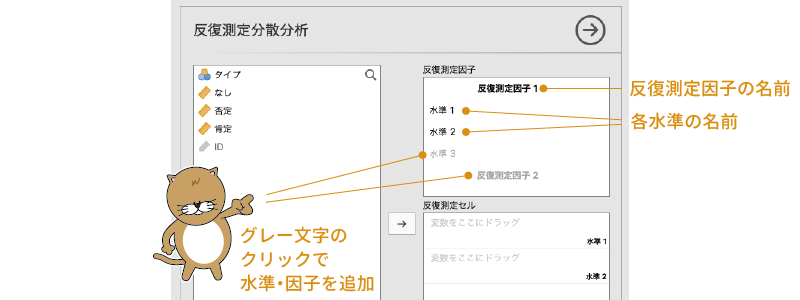
図6.52: 繰り返し要因の設定欄
まず,太字の「反復測定因子1」の部分は繰り返し要因の名前で,これをクリックすると要因の名前を設定することができます。名前を設定しなくても計算上は問題ありませんが,そのままだと結果を見たときにそれが何の要因かがわかりにくいので,わかりやすい名前をつけておくのがよいでしょう。今回のサンプルデータでは,繰り返し要因は「評価語」ですので,名前を「評価語」に設定します。
その下にある「水準1」や「水準2」では,この繰り返し要因に含まれている水準についての設定を行います。この「水準1」や「水準2」も,「反復測定因子1」の部分と同じくクリックすると名前を変えられるので,データに合わせてわかりやすい名前に設定しておきましょう。
今回の実験では,刺激条件の1つ目の水準は評価語が「なし」の条件なので,「水準1」の部分を「なし」に,2つ目の水準は「否定語」がセットになっている条件なので「否定」と設定します。
1つの要因に3つ以上の水準が含まれる場合には,グレーの文字の部分をクリックすることで新たな水準を追加することができます。今回のデータでは,評価語の条件として「なし・否定・肯定」の3つの水準がありますので,グレーの文字になっている「水準3」の部分をクリックして,そこに3つ目の水準の名前として「肯定」と入力しましょう。これで,1つ目の繰り返し要因に3つの水準を設定することができました。なお,この3つ目以降の水準については,その水準名の右側に表示される「×」の部分をクリックすることで削除することができます(図6.53)。
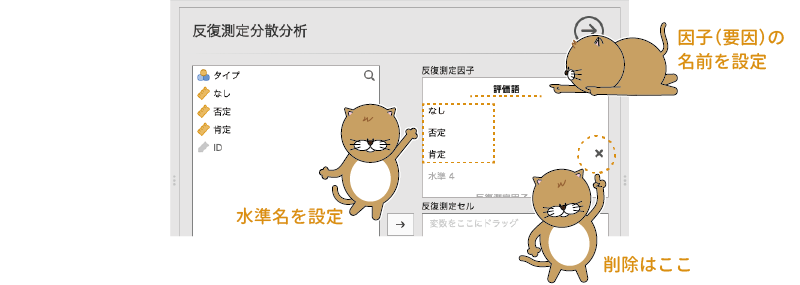
図6.53: 繰り返し要因の設定
また,今回の分析では繰り返しありの要因は1つしかありませんが,繰り返し要因が複数ある場合には,その下のグレーの文字で書かれた「反復測定因子2」の部分をクリックして要因名を設定すると,繰り返し要因を追加することができます。
繰り返し要因の個数やその水準数についての設定が終わったら,次に「反復測定セル」の欄で,それぞれの水準の測定値が入力されている変数を指定します。
今回の分析では繰り返し要因は1つしかありませんので,この部分の設定は単純です。「なし」の「変数をここにドラッグ」欄に「なし」を,「否定」の行に「否定」を,「肯定」の行に「肯定」をドラッグして移動します(図6.54)。
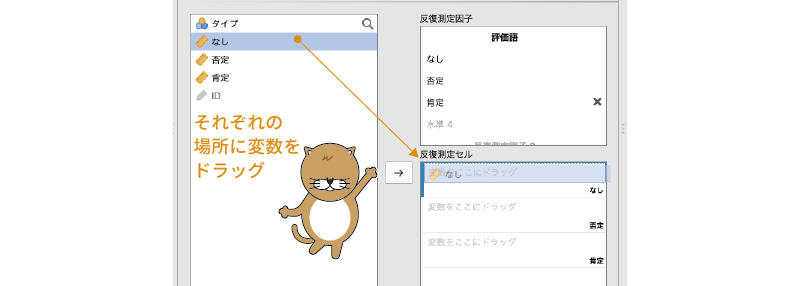
図6.54: 繰り返し要因の各水準に変数を設定
そして最後に繰り返しなし要因の設定です。ネコ派・イヌ派の「タイプ」の変数を,先ほどの「反復測定セル」の下にある「参加者間因子」へ移動します(図6.55)。これで分析の基本設定はおしまいです。

図6.55: 繰り返しなし要因を設定
なお,その下にもう1つ「共変量」という欄がありますが,今回の分析ではここは使用しません。これは分析に共変量を用いる場合の設定項目です。共変量については,この次の「共分散分析」のところで説明します。
6.3.3 分析結果
それでは結果を見てみましょう。反復測定分散分析では,結果は図6.56のような形で表示されます。
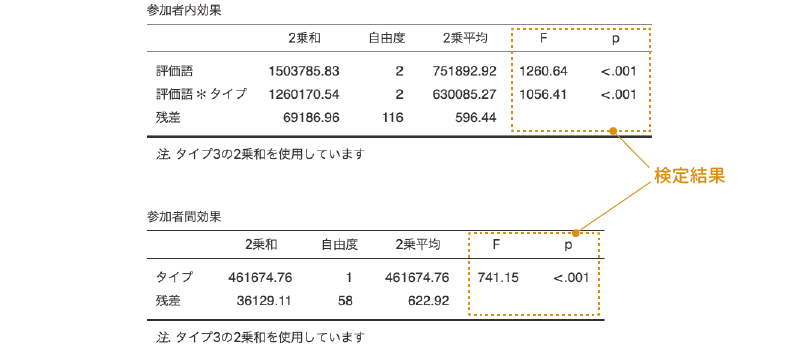
図6.56: 反復測定分散分析の結果
分析結果には,まず繰り返しありの要因が関係する主効果や交互作用についての表(参加者内効果)が,その下に繰り返しなしの要因の主効果や交互作用についての結果の表(参加者間効果)が示されます。
結果の表の見方は基本的には「分散分析」の場合と同じなのですが,上の表と下の表のそれぞれに「残差」があるのがわかるでしょうか。上の表の残差は,「評価語」の主効果についての個人差や「評価語×タイプ」の交互作用における個人差を集約した値で,繰り返し要因である「評価語」が関係する主効果や交互作用は,この残差を基準に検定が行われます。この場合,論文などで分析結果を報告するとしたら,統計値の部分は「F(2, 116) = 1260.64」のようになります。この場合の残差(誤差)の自由度は,参加者内効果の「残差」のものを使用します。
なお,ここでは上の表には「残差」は1つしかありませんが,繰り返し要因が2つ以上ある場合には,それぞれの繰り返し要因の主効果における個人差,そしてそれら繰り返し要因同士の交互作用における個人差が算出されますので,1つの表に「残差」が複数表示されることになります。その場合,それぞれの主効果や交互作用のすぐ下にある「残差」の値がそれらの主効果や交互作用の検定で用いられる残差(誤差)になります。
また,下の表の「残差」は,「評価語」全体(3水準の平均値)における各参加者のばらつきを集約した値で,これは実験条件とは無関係な個人間のばらつきです。繰り返しなしの要因のみで構成される主効果や交互作用の場合には,こちらの残差を基準に検定が行われます。こちらの検定結果を論文などで示す場合には,統計値の部分は「F(1, 58) = 741.15」となります。この検定での誤差(残差)の自由度は,この参加者間効果の表にある値を使用してください。
この分析の結果,「評価語」,「タイプ」の主効果と,「評価語×タイプ」の交互作用のいずれも有意確率「p<.001」で有意であることが示されました。
6.3.4 分析の詳細設定
ここからは,反復分散分析における設定項目について説明します。まず,設定画面の変数一覧の下にある項目から見ていきましょう(図6.57)。

図6.57: 反復測定分散分析の詳細設定項目
効果量
設定画面の効果量では,効果量について設定します。反復測定分散分析では,効果量として「一般化\(\eta^2\)(一般化イータ2乗)」,「\(\eta^2\)(イータ2乗)」,「偏\(\eta^2\)(偏イータ2乗,\(\eta^2_p\))」の3種類を算出できます。
η²(イータ2乗)
順番が前後しますが,まずは\(\eta^2\)(イータ2乗)から見ていきましょう。\(\eta^2\)の値は「分散分析」の場合と同じで,これは各主効果,交互作用の2乗和をデータ全体の2乗和で割った値,つまり,そのデータ全体に占める各主効果,交互作用の比率です。
偏η²(偏イータ2乗)
\(\eta^2_p\)(偏イータ2乗)の値も基本的に「分散分析」での値と同じで,主効果,交互作用の2乗和をそれ自体と残差の2乗和の合計で割った値です。ただし,反復測定分散分析では複数種類の残差が算出されるため,\(\eta^2_p\)はそれぞれの主効果,交互作用と,それに関係する残差の2乗和を用いて算出されます。
一般化η²(一般化イータ2乗)
ただ,その場合,\(\eta^2_p\)では繰り返しなしの要因と繰り返しありの要因で効果量の算出基準が異なることになるため,効果の大きさを比較することが困難になります。そこで,そのような問題を解決するために考案された指標が\(\eta^2_G\)(一般化イータ2乗)です。この値は,繰り返しありの要因となしの要因の両方の残差を用いて各主効果や交互作用の効果量を算出します。
なお,この\(\eta^2_G\)を算出する場合には,それぞれの要因が操作要因であるのか測定要因であるのかを区別する必要があります。操作要因とは,実験者が設定した実験条件などが含まれる要因を指し,測定要因は参加者が持っている特性(性別,年齢など)によって分類される要因を指します。たとえば,今回の例における評価語要因(なし・否定・肯定)は,実験者が操作して設定したものですから「操作要因」ということになります。なお,繰り返し要因は実験者が操作して設定するものなので,つねに操作要因として扱われます。
それに対し,参加者のタイプ(ネコ派・イヌ派)は実験者が操作したものではなく,これはそれぞれの参加者が持っている特性です。ですので,この要因は「測定要因」ということになります。また,測定要因との交互作用は,すべて測定要因とみなされます。このようにして考えると,今回のサンプルデータでは,評価語の要因が操作要因,タイプの主効果と評価語×タイプの交互作用が測定要因ということになります。
このように,操作要因と測定要因の区別はその内容によって判断されるので,これは統計ソフトが自動で判断できるようなものではなく,分析者が自分判断して指定しなければなりません。しかし,少なくとも現時点において,jamoviにはこれらの区別を指定する設定項目がなく,この設定項目における\(\eta^2_G\)の値は,すべての要因を操作要因とみなして算出されたものになっています。そのため,ここで算出される\(\eta^2_G\)は,操作要因(今回の場合は評価語の主効果)については適切な値といえるのですが,測定要因(タイプの主効果,評価語×タイプの交互作用)にはついて適切な値ではありません。その点には注意が必要です。
従属変数ラベル
反復測定分散分析の設定画面にある「従属変数ラベル」は,推定周辺平均値をグラフに示す際に使用する従属変数名を設定します。繰り返しなしの場合,分析に使用される従属変数はデータファイルでも1列に入力されているため,その変数の名前をそのまま従属変数の名前としてグラフの縦軸に使用することができます。しかし反復測定分散分析の場合,従属変数が複数列に入力されているために,単純に分析に使用されている変数の名前を用いるといったことができません。
そこで,jamoviでは,この従属変数ラベルに入力された名前をグラフの縦軸ラベルとして使用します。この設定部分は分析結果には影響しませんからそのままでもよいですが,今回の分析の場合は「反応時間 (ms)」としておくのがわかりやすいでしょう(図6.58)。

図6.58: グラフ用の縦軸ラベルの設定
6.3.5 モデル
の部分は,繰り返しありの要因とそうでない要因で設定欄が分かれているのが異なるくらいで「分散分析」の場合と基本的な設定方法は同じですので,ここでは説明を省略します(図6.59)。
図6.59: 分析モデルの設定
なお,「分散分析」では「2乗和」の部分でタイプ1からタイプ3までの方法を選択することができましたが,反復測定分散分析の場合には,分析に使用できるのはタイプ2と3のみです。
6.3.6 前提チェック
反復測定分散分析のには,次の項目が含まれています(図6.60)。

図6.60: 反復測定分散分析の前提チェック
- 球面性検定 球面性検定を行います。
- 球面性補正 球面性の前提が満たされない場合における補正方法を指定します。
- なし 補正は行いません
- グリーンハウス=ガイザー グリーンハウス=ガイザー推定による補正を行います。
- ヒューン=フェルト ヒューン=フェルト推定による補正を行います。
- 等質性検定 分散の等質性の検定を行います。
- Q-Qプロット 正規Q-Qプロットを作成します。
「分散分析」の設定画面にはなかった項目がいくつかありますので,これらについて簡単に見ておきましょう。
球面性検定
繰り返しなしの分散分析で各水準の分散が等質であることが分析の前提としてあったように,反復測定分散分析では繰り返し要因の各水準間で「差の分散が等しい」ことが必要とされます。このような前提は球面性の仮定と呼ばれ,球面性検定ではこの前提が満たされているといえるかどうかについて検定します。球面性検定は,モークリー検定とも呼ばれます。
この項目にチェックを入れると,図6.61のような形で検定結果が表示されます。

図6.61: 球面性検定の結果
結果の表の1番左にある「モークリーのW」が球面性仮説の検定における統計量で,その隣のpの値が有意確率です。このpの値が有意水準を下回る場合には,球面性の前提が満たされていないと判断され,これを修正するための補正が行われます。また,pの隣にある「グリーンハウス=ガイザーの\(\varepsilon\)」と「ヒューン=フェルトの\(\varepsilon\)」は,球面性の前提が満たされない場合の修正に使用される値です。
今回の分析結果では,p=0.589で検定結果は有意ではありませんので,球面性仮説に関する補正を行う必要はありません。
球面性補正
今回の分析結果のように球面性検定の結果が有意でない場合には,繰り返し要因についての分析結果をそのまま採用することができるのですが,球面性検定の結果が有意だった場合には,球面性検定の結果の表にある\(\varepsilon\)(イプシロン)という値を用いて自由度を修正し,p値を算出するという方法がとられます。
\(\varepsilon\)の算出の仕方にはいくつかの方法がありますが,jamoviでは次の方法を利用することができます。
なし
この項目がオンになっている場合には,球面性補正なしのp値が算出されます。反復測定分散分析の初期設定では,この項目がオンになっています。球面性の前提が満たされている場合など,球面性に関する補正が必要ない場合にはこの値を使用します。
グリーンハウス=ガイザー補正
この項目にチェックを入れると,グリーンハウス=ガイザーの\(\varepsilon\)を用いて修正した自由度と,それを元にした2乗平均やF,p値などが算出されます(図6.62)。
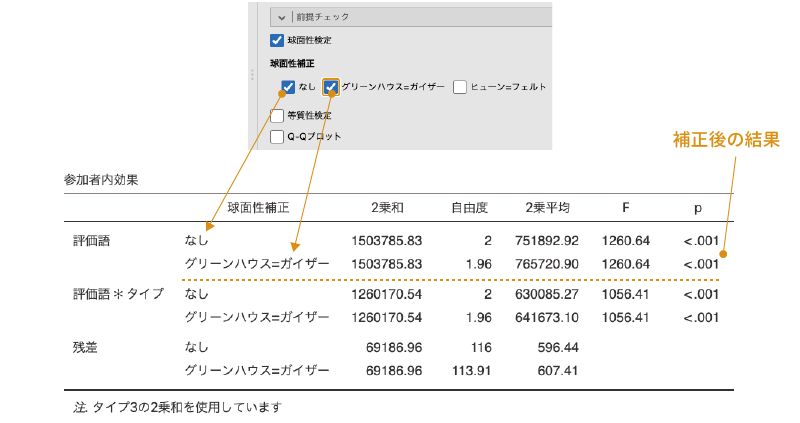
図6.62: 球面性補正後の結果
このグリーンハウス=ガイザーの\(\varepsilon\)による修正は,球面性の前提が満たされない場合の補正方法としてもっとも一般的なものです。
ヒューン=フェルト補正
球面性の補正方法としてはグリーンハウス=ガイザーの\(\varepsilon\)を用いるのが一般的だといいましたが,この方法は,\(\varepsilon\)の値が大きい場合(球面性からのずれが小さい場合)には調整が強くなりすぎるといわれています。そしてその問題を修正したものがヒューン=フェルトの\(\varepsilon\)です。ヒューン=フェルトの\(\varepsilon\)は,グリーンハウス=ガイザーの\(\varepsilon\)に対して修正を加えることによって得られる値です。
この項目にチェックを入れると,ヒューン=フェルトの\(\varepsilon\)で修正した自由度に基づく検定結果が表示されます。なお,今回の分析結果ではヒューン=フェルトの\(\varepsilon\)は1.00ですので,表示される結果は補正を行わない場合と同じになります。
等質性検定
この「等質性検定」の項目にチェックを入れると,繰り返しなしの要因に関する分散の等質性の検定結果(ルビーン検定の結果)が表示されます(図6.63)。

図6.63: 分散の等質性検定の結果
結果の表を見ると「なし」や「否定」など,繰り返し要因である評価語の各水準名が並んでいますが,これは評価語の要因について分散の等質性の検定をしているのではなく,評価語の各水準において,繰り返しなし要因である「タイプ(ネコ派・イヌ派)」について,分散の等質性の検定を行った結果が表示されているのです。
分析に含まれている要因に繰り返しなしの要因が1つもない場合には,この項目にチェックを入れても結果は「NaN(非数)」となって数値は表示されません。
今回の分析結果では,どの水準においても参加者のタイプで有意に分散が異なるということはありませんでした。
6.3.7 事後検定
このの設定項目は「分散分析」の場合とまったく同じですので,ここでは説明を省略します。詳細については「分散分析」の「事後検定」の部分を見てください。
6.3.8 推定周辺平均
このの項目も,設定項目自体は「分散分析」の場合と同じです。ただし,推定周辺平均のグラフを作成した場合には,縦軸(数値軸)のラベルとして「従属変数ラベル」に設定した名前が使用されます(図6.64)。
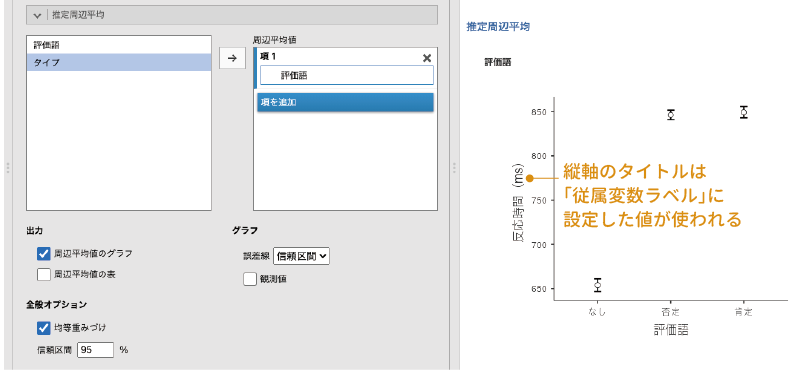
図6.64: 推定周辺平均のグラフと縦軸ラベル
6.3.9 オプション
設定画面の一番下にあるには「グループの要約」という設定項目が含まれています。この項目にチェックを入れると,繰り返しなし要因の各水準における標本サイズや分析から除外された測定値の個数などの情報が表示されます(図6.65)。

図6.65: グループの要約