9.4 確認的因子分析

探索的因子分析によって得られる因子は，あくまでも分析に使用したデータに基づくものであって，それが普遍的な真実であるというわけではない点には注意が必要です。探索的因子分析の結果というのは一般に不安定なことが多く，分析に使用する変数が増えたり減ったりした場合や，別の集団を対象とした調査結果を分析した場合などには，抽出される因子の結果が変わることもよくあるのです。

となると，分析で得られた因子モデルの正しさを別のデータで確かめたい，という考えが当然ながら生じてくるでしょう。ではその場合，新たに収集したデータを用いて探索的因子分析を行えばいいかというとそうではありません。探索的因子分析は，その分析データをもっともうまく説明できると考えられる因子を探索的に抽出する方法であって，因子モデルが正しいかどうかを確かめるための方法ではないからです。

そして，このようにすでにある因子モデルが別のデータにおいてもあてはまるかどうかを確かめたい場合に使用されるのが，確認的因子分析と呼ばれる分析手法です。

9.4.1 考え方

ここでは，先ほどの探索的因子分析で用いたサンプルデータ（オタク傾向）の分析結果をもとに，確認的因子分析の考え方を見ていきましょう。先ほどの分析では，9つの質問への回答の背後に3つの共通因子が推定されました。そして，9つの質問のうち，Q1からQ3は「収集欲求」因子のみの負荷が高く，Q4からQ6は「非社交性」因子，Q7からQ9は「熱中傾向」因子のみの負荷が高いというように，各質問への回答には3つの因子のうちいずれか1つのみが強く影響している単純構造にあることが示されました。

そして，このような構造が，海外のオタクにおいてもあてはまるといえるかどうかを知りたいとしましょう。そこで，前回の調査で使用した9つの質問を英訳し，英語圏に住む成人400名を対象に調査を実施しました。その結果がこのサンプルデータ（factor_data04.omv）に入力されています（図9.54）。

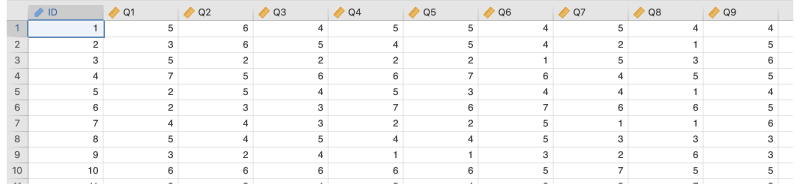
サンプルデータ

図9.54: サンプルデータ

  • ID　回答者のID
  • Q1　I’m a thorough researcher when it comes to a subject I’m interested in.
  • Q2　I’m willing to spend a lot of time and money to get what I want.
  • Q3　I want to collect all the items and goods related to my hobby.
  • Q4　Sometimes I think fictional characters are better than real people.
  • Q5　I enjoy my hobbies more than being with people.
  • Q6　It’s better to communicate with people online than in person.
  • Q7　Sometimes I get too enthusiastic and stun the people around me.
  • Q8　I can’t stop talking about my hobbies.
  • Q9　Sometimes I get so absorbed that I lose control of myself.

このデータを先ほどの因子モデルでうまく説明できるかどうかを見るためには，まず分析に使用する因子モデルをはっきりさせておく必要があります。

前回の因子分析結果を単純な模式図として示すと図9.55のようになります。まず，「Q1」から「Q3」は「収集欲求」因子の影響を強く受けていました。他の2つの因子からもわずかに影響を受けていましたが，それらは非常に弱いので，ここでは省略します。

収集欲求因子と観測変数の関係

図9.55: 収集欲求因子と観測変数の関係

この図では，因子を楕円で，各観測変数（質問への回答データ）を四角で示しています。因子と各変数は線（パス）で繋がれており，このパスは観測変数のほうに向かう矢印の形になっています。この矢印の向きは，変数間の影響の向きを表しています。因子分析の考え方では，各観測変数に対して因子が影響を及ぼしていると考えますので，矢印は因子から各観測変数に向かう形になるのです。

同様に，「Q4」から「Q6」は「非社交性」因子，「Q7」から「Q9」は「熱中傾向」因子の影響を強く受けていました（図9.56）。

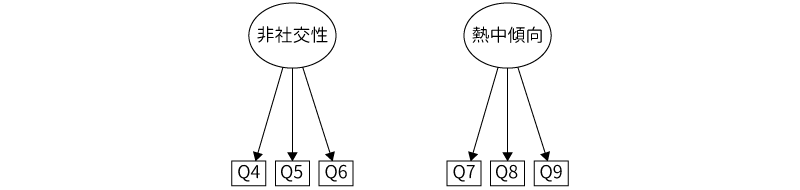
非社交性因子，熱中傾向因子と観測変数の関係

図9.56: 非社交性因子，熱中傾向因子と観測変数の関係

また，これらの因子の間には，中程度からやや弱目の相関関係がありました。相関関係はお互いに関連があるということなので，ここではパスを両矢印で示します（図9.57）。

共通因子間の関係

図9.57: 共通因子間の関係

このようにして因子間と観測変数間の関係を図示したものはパス図と呼ばれます。このパス図は先ほどの因子分析結果を単純化して示したものですが，これが確認的因子分析において使用される分析モデルになるのです。確認的因子分析では，このような単純化された因子モデルを用いて，このモデルでデータをうまく説明できるかどうかを確かめます。

9.4.2 分析手順

確認的因子分析は，一般に高価な専用ソフトウェアを使用するか，分析モデルをコンピュータープログラムのような形で書き表して実行するような形でしか利用できない場合がほとんどですが，jamoviではこれを驚くほど簡単に実行することができます。

jamoviで確認的因子分析を実行するには，分析タブの「inline 因子分析」から「確認的因子分析」を選択します（図9.58）。

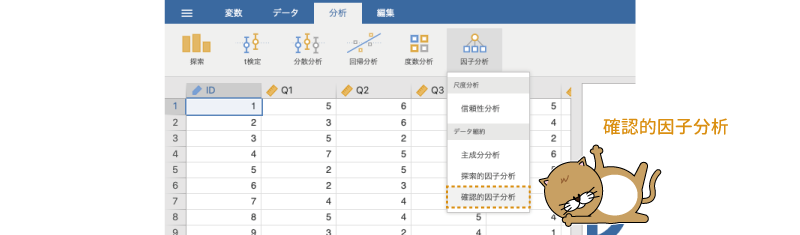
確認的因子分析の実行

図9.58: 確認的因子分析の実行

すると，次の設定画面が表示されます（図9.59）。

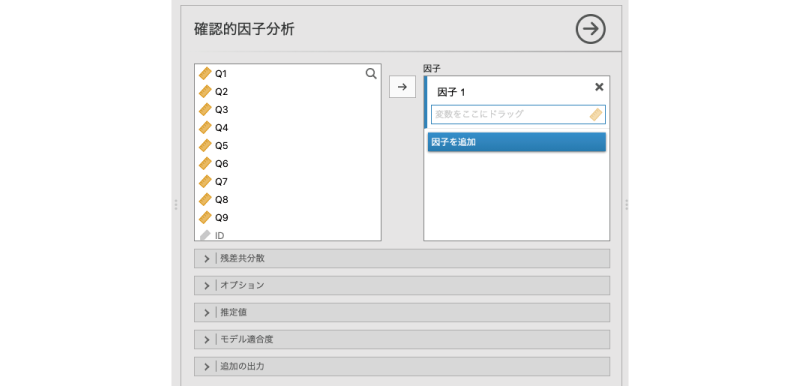
確認的因子分析の設定画面

図9.59: 確認的因子分析の設定画面

この画面右側の「因子」の部分に，分析モデルにそって変数を設定します。

初期状態では，「因子」の部分には「因子1」しかありませんが，その下にある因子を追加をクリックすると，因子を追加することができます。今回の分析モデルには3つの因子がありますので，因子を追加を2回クリックして因子を2つ追加します（図9.60）。

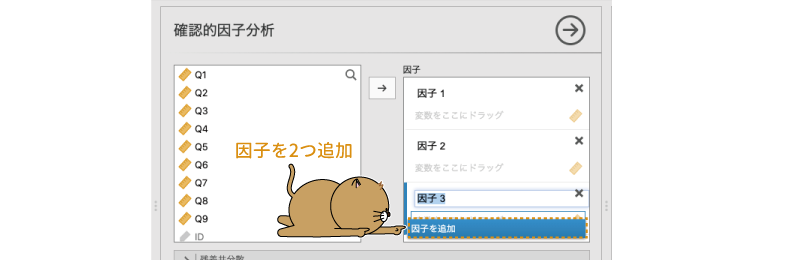
因子を2つ追加

図9.60: 因子を2つ追加

次に，作成した因子の名前を設定します。因子の名前は「因子1」や「因子2」のままでも計算上は問題ありませんが，結果を見間違えたりしないよう，きちんと因子名を設定しておいたほうがよいでしょう。ここでは，「因子1」を「収集」，「因子2」を「非社交」，「因子3」を「熱中」としておきます（図9.61）。

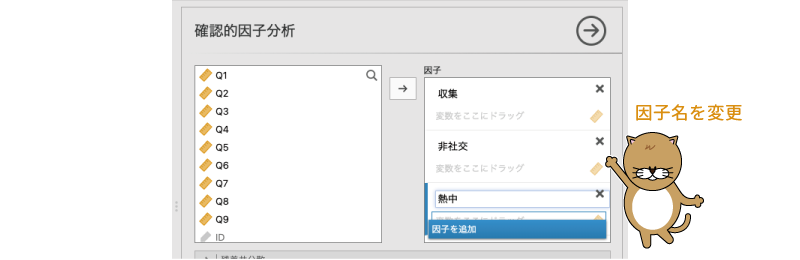
因子の名前を変更

図9.61: 因子の名前を変更

因子名の設定が終わったら，それぞれの因子に関連する変数を指定していきます。まず，「収集」因子の負荷が高いと考えられるのは「Q1」，「Q2」，「Q3」の3つですので，この3つを「収集」の「変数をここにドラッグ」の部分にマウスでドラッグして移動します（図9.62）。

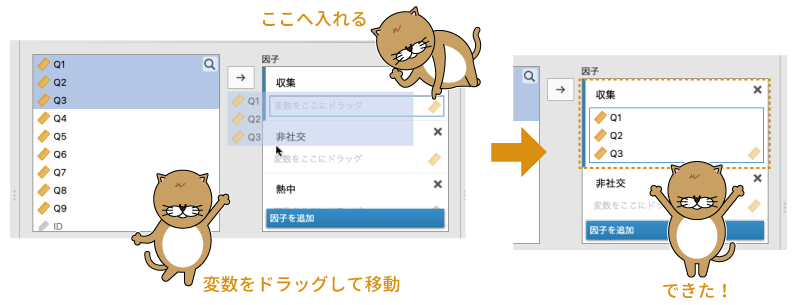
因子1に変数を設定

図9.62: 因子1に変数を設定

同様にして，「非社交」と「熱中」因子も変数を指定します（図9.63）。

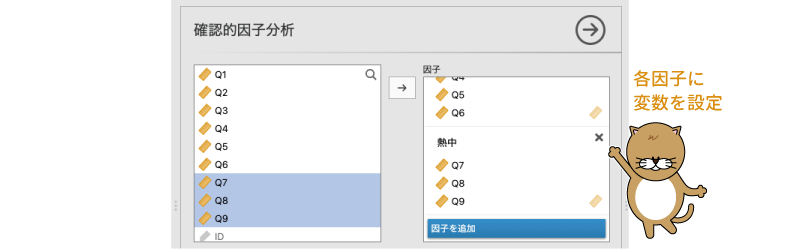
すべての因子に変数を設定

図9.63: すべての因子に変数を設定

基本的な分析設定はこれでおしまいです。

9.4.3 分析結果

それでは分析結果について見てみましょう。基本設定による分析では，図9.64のような結果が表示されます。いろいろな値が表示されているので，1つ1つ見ていきましょう。

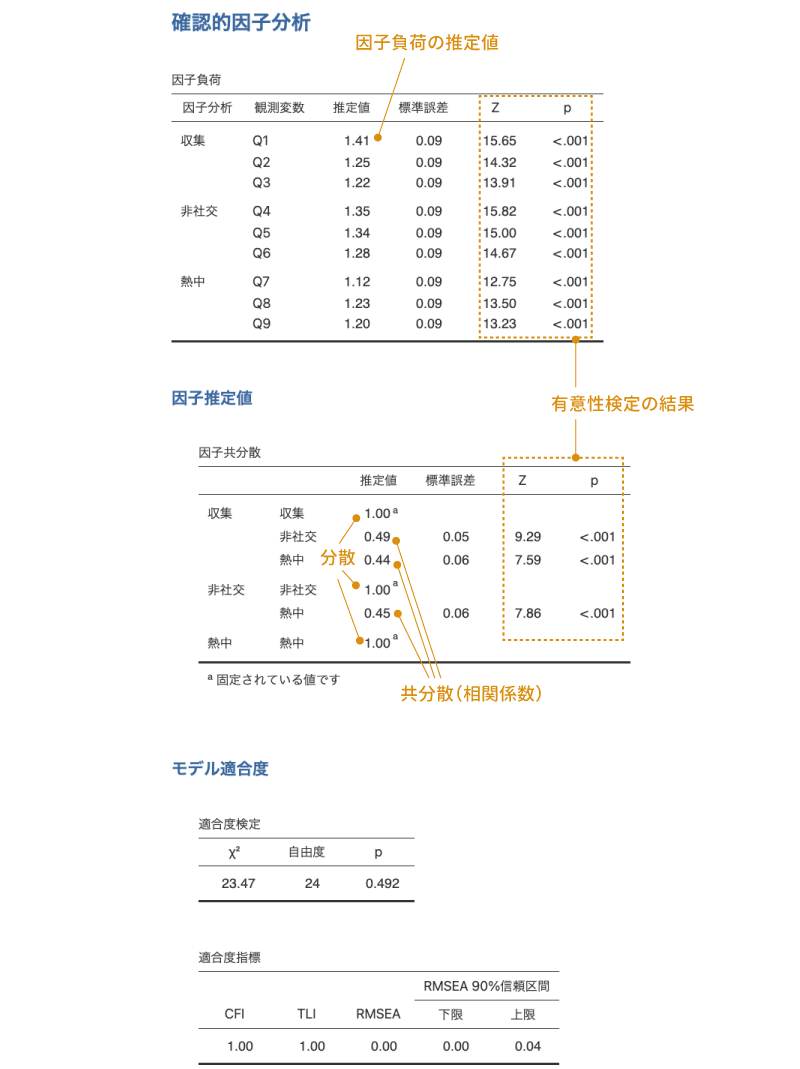
確認的因子分析の結果

図9.64: 確認的因子分析の結果

1つ目の「因子負荷」の表には，それぞれの因子から観測変数（各質問）への負荷量の推定値，標準誤差，標準得点（Z），有意確率（p）が示されています。この結果では，すべての値で負荷量の推定値が1を超えていますが，これは分析結果に問題があるわけではなく，この負荷量の値が標準化されていないものだからです。

この結果では，それぞれの因子負荷量について「因子負荷が0である」という帰無仮説を用いた検定の結果が示されており，いずれの検定も有意確率（p）は「<.001」で有意になっています。

2つ目の「因子共分散」の表には，「推定値」の部分に因子の分散および因子間の共分散の値が示されています。なお，この表では各因子の分散は1.00に固定されており，この表に示されているのは因子間の相関係数になっています。各因子間の相関係数についても，因子負荷と同様に標準誤差と標準得点（Z），有意確率（p）の値が示されており，それぞれの有意性検定（帰無仮説：相関係数は0である）の結果を見ることができます。

3つ目と4つ目の表には，この分析モデルのデータへの適合度に関する情報が表示されています。3つ目の表はモデルとデータのずれの大きさについての検定で，これは探索的因子分析の「モデル適合度指標」の部分で説明したものと同じです。この検定では\(\chi^2\)が小さく，検定結果が有意でないことが望ましい結果です。今回の分析結果では有意確率p=0.492で検定結果は有意ではありませんので，分析モデルとデータのずれは0でないといえるほど大きなものでない（ずれは小さい）といえます。

その下の「適合度指標」には，モデルのデータの適合度に関する代表的な指標が示されています（図9.65）。

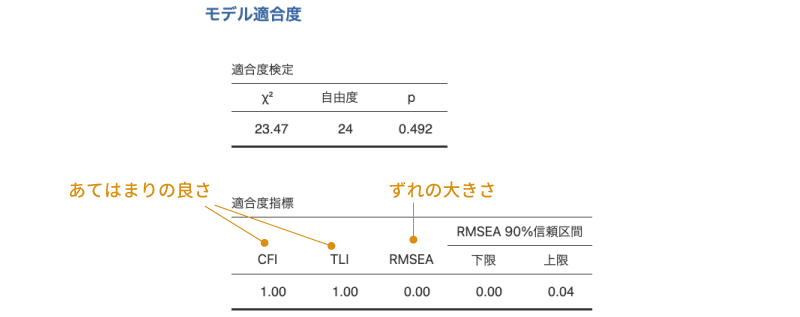
適合度関連の結果

図9.65: 適合度関連の結果

この表に示されている値のうち，2つ目のTLIと3つ目のRMSEAについては，探索的因子分析の適合度指標のところで説明したものと同じです。

表の1つ目のCFI（比較適合度指標）は，TLIと同様に独立モデル（因子と各変数の間の関係をまったく考えないモデル）に比べてどの程度あてはまりが改善しているかを0から1までの数値になるようにして算出した値で，この値が1に近いほどモデルがデータにうまくあてはまっていることを意味します。一般に，この値が0.90または0.95以上である場合に適合度が高いとみなされます。

この分析結果では，適合度指標はCFI=1.00，TLI=1.00，RMSEA=0.00[0.00-0.04]で，いずれも適合のよさを示しています。したがって，今回の外国人を対象としたデータの場合にも，前回の分析結果で得られた3つの共通因子でうまく説明ができる，つまり，外国人の場合にも日本人と同じオタク傾向の3因子モデルがあてはまるということになります。

では，ここからは分析の詳細設定について見ていきましょう。次の設定を適切に使用することで，分析結果についてのより詳しい情報が得られます。

9.4.4 残差共分散

| 残差共分散の設定項目は，因子によって説明しきれない残差（独自因子）の間で共分散（または相関係数）を算出したい場合に使用します。この項目を展開すると，図9.66のような画面が表示されます。

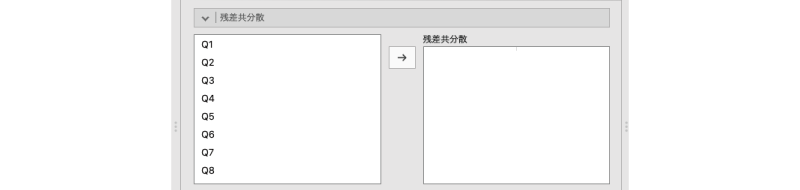
残差共分散の設定

図9.66: 残差共分散の設定

この残差共分散（誤差共分散とも呼ばれます）を算出するには，ここで残差の共分散を算出したい変数のペアを選択し，それを右側の「残差共分散」の欄に移動します。なお，「inline 回帰分析」メニューの「相関行列」で相関係数を算出する場合とは異なり，ここでは共分散を算出させたい変数のペアを個別に指定する必要があります（図9.67）。

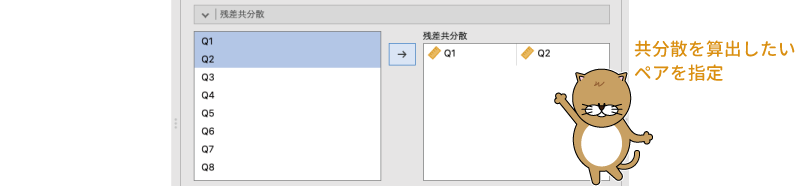
残差共分散の設定の例

図9.67: 残差共分散の設定の例

残差共分散を算出するのはモデルの適合度を向上させるためであることがほとんどだと思われますが，残差共分散は因子で説明しきれない部分における変数間の関係であるため，残差共分散を多数算出する必要がある場合には，必要な因子がモデルの中に組み込まれていないなど，想定する因子モデルに問題がある可能性があります。

9.4.5 オプション

| オプションでは，分析における欠損値の扱いと，計算上の制約条件についての設定を行います（図9.68）。

オプションの設定

図9.68: オプションの設定

  • 欠損値の処理
    • 完全情報最尤推定法　他の測定値から欠損値を推定した上で分析します。
    • 行全体を除外　欠損値が含まれるデータ行全体を分析から除外します。
  • 制約
    • 因子の分散を1に固定　因子の分散を1に固定した場合の計算結果を表示します。
    • 最初の係数を1に固定　各因子の最初の変数の係数を1に固定した場合の計算結果を表示します。

欠損値の処理方法

今回のサンプルデータには含まれていませんが，分析データに欠損値（データが欠落している部分）がある場合，その欠損値をどのように扱うかによって分析結果に影響が生じます。jamoviの確認的因子分析では，分析データに欠損値が含まれている場合，その値を完全情報最尤推定法と呼ばれる方法によって他のデータ値から推定し，その値を欠損部分に代入することによって分析を行います。

欠損値に対して推定値を代入せず，欠損のままにしておきたい場合には，「行全体を除外」に設定を変更してください。完全情報最尤推定法による補完を行うのと，欠損がある場合にデータ行ごと分析から除外するのとでどちらがよいかは一概にはいえませんが，近年，とくに確認的因子分析においては，完全情報最尤推定法など，何らかの形で欠損値を補完して分析することが多いようです。

推定における制約

探索的因子分析でも，何らかの形で計算のための条件や前提を設定しないことには計算結果が1つに定まらなかったのと同様に，確認的因子分析でもまったくの条件なしにはモデルに関する推定ができません。

計算結果を収束させるために，確認的因子分析では「因子の分散を1」に固定するか，「各因子の最初の係数（負荷量）を1」にするか，いずれかの方法で計算を行います。jamoviの分析設定では，「因子の分散を1に固定」が初期設定値になっています。その場合，当然ですが表示される計算結果ではすべての因子で分散が1になります。

もし因子の分散という情報が分析上重要である場合には，「最初の係数を1に固定」に設定して計算を行うことになるでしょう。その場合，各因子の分散の値は算出されますが，各因子の最初の変数では，その係数（因子負荷量）はすべて1になります。

なお，分析結果として標準化された推定値（標準化推定値）を使用する場合には，どちらの場合も最終的な計算結果は同じになります。

9.4.6 推定値

| 推定値では，因子や残差の推定値に関する設定を行います（図9.69）。

推定値の設定

図9.69: 推定値の設定

  • 結果
    • 因子共分散　因子の分散，および因子間の共分散または相関係数を算出します。
    • 因子の切片　因子の切片についての推定量を算出します。
    • 残差共分散　残差の分散，および指定した変数間での残差の共分散，または相関係数を算出します。
    • 残差の切片　残差の切片についての推定量を算出します。
  • 統計量
    • 検定統計量　推定した各係数についての有意性検定の結果を表示します。
    • 信頼区間　各係数について，信頼区間の算出を行います。
    • 標準化推定値　各係数について，標準化された値を算出します。

結果

この画面の結果の部分では，因子と各観測変数の残差の分散・共分散と切片の算出結果を表示するかどうかについての設定を行います。

この設定で「因子共分散」にチェックを入れた場合には，各因子の分散と，因子間の共分散または相関係数が表示されます。このとき，先ほどの| オプションのところで推定のための制約を「因子の分散を1に固定」に設定した場合には，結果に表示される値は各因子の分散（すべて1.00で固定）と，因子間の相関係数になります。これに対し，制約条件を「最初の係数を1に固定」に設定した場合には，結果の表には各因子の分散と因子間の共分散の値が表示されます。

その下の「因子の切片」の部分にチェックを入れると，因子の切片（因子の平均値）についての情報が表示されるのですが，jamoviの現在のバージョンでは確認的因子分析で複数グループのデータを同時に分析するといったことはできませんので，この値はいずれの因子においても1.00で固定になります。そのため，この項目については現在のところ使い道はありません。

3つ目の「残差共分散」の項目にチェックを入れると，各観測変数の残差の分散が表示されます。また，| 残差共分散の設定で共分散を算出するように設定した場合には，設定した観測変数のペアについて，算出された共分散の値が表示されます。

一番下の「残差の切片」の部分にチェックを入れると残差の切片についての情報が表示されるのですが，その推定値および標準誤差は，どのような場合にもすべて観測変数の平均値と標準誤差の値に等しくなります（図9.70）。そのため，この項目についても今のところ使い道はなさそうです。

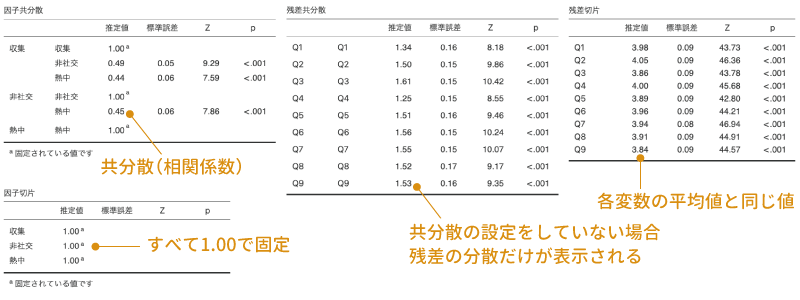
各設定項目の出力結果の例

図9.70: 各設定項目の出力結果の例

統計量

| 推定値右側の統計量の部分では，係数の推定に関する設定を行うことができます。1つ目の「検定統計量」にチェックを入れると，算出した係数（分散や共分散も含む）の推定値について，その係数が0でないかどうかの有意性検定の結果が表示されます。確認的因子分析では，いずれの係数についても標準得点zを用いた検定が行われます。

2つ目の「信頼区間」にチェックを入れると，それぞれの係数について指定した幅の信頼区間が表示されます。

3つ目の「標準化推定値」にチェックを入れると，各係数を標準化した値が表示されます。この標準化推定値の値は，| オプションのところで計算上の制約として「因子の分散を1に固定」を選択した場合にも「最初の係数を1に固定」を選択した場合にも同じになります（図9.71）。

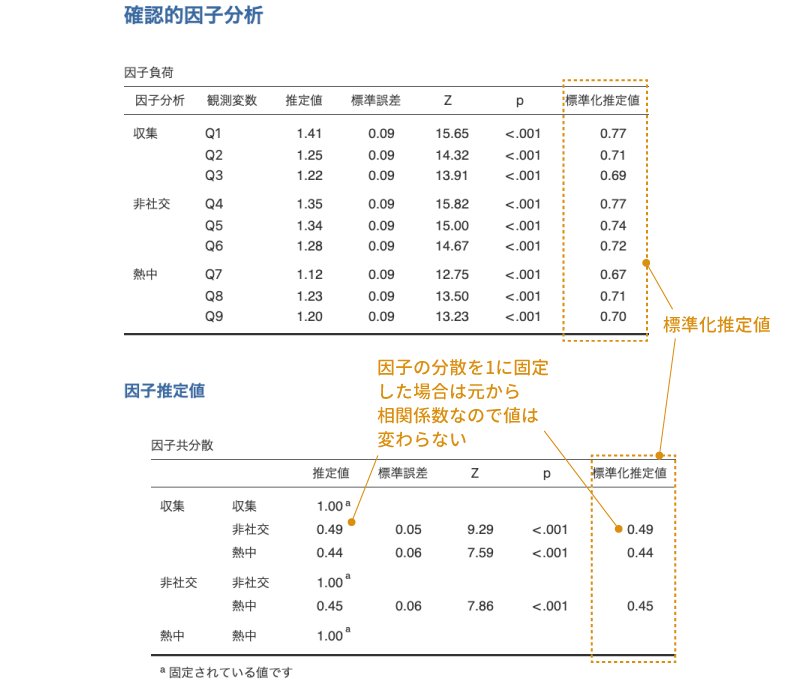
標準化推定値

図9.71: 標準化推定値

心理学の研究論文では，確認的因子分析の結果を報告する際にはこの標準化推定値を用いることが多いようです。考え方説明のところで用いた因子モデルの図に標準化推定値を示すと，分析結果は図9.72のようになります。

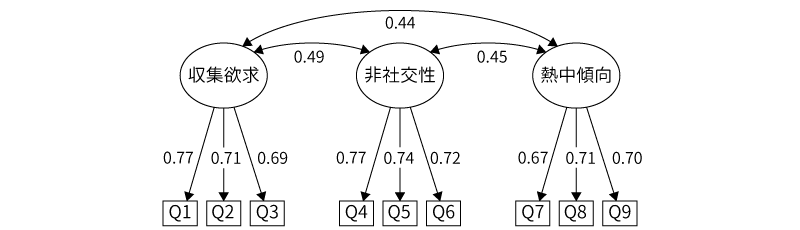
分析結果のパス図

図9.72: 分析結果のパス図

9.4.7 モデル適合度

| モデル適合度では，モデル全体の適合度に関する情報の設定を行います（図9.73）。

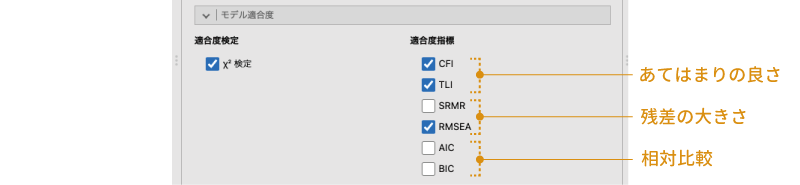
モデル適合度の設定項目

図9.73: モデル適合度の設定項目

  • 適合度検定
    • \(\chi^2\)検定　モデル適合度についての\(\chi^2\)検定の結果を表示します。
  • 適合度指標
    • CFI　モデルのあてはまりのよさについての指標（比較適合度指標）を示します。
    • TLI　モデルのあてはまりのよさについての指標（タッカー=ルイス指数）を示します。
    • SRMR　モデルの残差の大きさについての指標（標準化残差2乗平均平方根）を示します。
    • RMSEA　モデル残差の大きさについての指標（近似誤差2乗平均平方根）を示します。
    • AIC　モデル残差の相対的な大きさについての情報（赤池情報量規準）を示します。
    • BIC　モデル残差の相対的な大きさについての情報（ベイズ情報量規準）を示します。

適合度検定

画面左側の「適合度検定」の部分では，モデルの適合度に関して\(\chi^2\)検定を行うかどうかを設定できます。この検定では，「このモデルはデータがもつ情報を完全に説明できている（モデルによる残差が0である）」が帰無仮説ですので，この検定結果は有意にならない（pが0.05より大きい）ことが望ましいという点に注意してください。

今回のサンプルデータでは\(\chi^2(\textsf{21})=\textsf{17.37}\)で，有意確率p=0.688ですから，検定結果は有意ではありません。したがって，分析モデルでデータをうまく説明できている（モデルとデータのずれは大きくない）といえます。

なお，探索的因子分析のところでも説明しましたが，この\(\chi^2\)検定の結果は分析に使用する観測変数がたくさんある場合や標本サイズが大きい場合には有意になりやすい傾向があります。そのため，この検定結果が有意になっていたらだめだというわけでは必ずしもありません。モデルの適合度は，他の適合度指標と合わせて総合的に判断します。

適合度指標

画面右側の適合度指標の部分では，適合度指標として表示させる値を選択します。

CFI，TLI

CFIとTLIについては，すでに探索的因子分析のところで説明しました。これらの値は，分析モデルの適合度が独立モデル（因子と観測変数がまったく無関係なモデル）に比べてどれだけ改善したかを示す値で，この値が1に近いほどあてはまりがよいことを意味します。一般には，0.9以上あるいは0.95以上の場合にあてはまりが良好であるとみなされます。

SRMR，RMSEA

SRMRとRMSEAは残差の大きさに関する指標で，これらは0に近いほどよいということになります。RMSEAについては探索的因子分析のところで説明したとおりです。SRMRは，データから求められる共分散と推定モデルの共分散の差をもとに算出されます。これらの指標は，いずれの場合も算出した結果が0.05未満である場合にあてはまりが良好であるとみなすのが一般的です。

AIC，BIC

AICとBICについては，回帰分析のモデル適合度 で説明したとおりです。これらはモデルの残差の大きさを表す値ですが，この値未満であればよいというようなものではなく，複数のモデル候補の間で相対的にあてはまりのよさを判断するための指標です。いくつかのモデル候補がある場合には，その中でこれらの値がもっとも小さくなるモデルを選択するのが一般的です。

このように，確認的因子分析ではさまざまなモデル適合度指標を算出することができるのですが，逆にいえばこれは，この値さえ求めておけばよいというような定番の指標がないということでもあります。研究論文でも，モデル適合度の指標として\(\chi^2\)検定の結果，あてはまりのよさの指標（CFIやTLI）を1つ以上，残差の大きさの指標（SRMRやRMSEA）を1つ以上の3種類の指標をセットで報告するのが一般的です。

また，適合度指標としてどれを報告するかには流行（？）のようなものもあり，あてはまりのよさの指標として少し前まではGFIとAGFIという指標が報告されることが多かったのですが，近年ではそうでもないようです。少なくとも，それらの指標はjamoviのオプションには含まれていません。

9.4.8 追加の出力

| 追加の出力では，分析結果に基づいてモデルの適合度を向上させるための参考指標などについて設定することができます（図9.74）。

追加の出力に関する設定項目

図9.74: 追加の出力に関する設定項目

  • モデルの事後修正
    • 相関行列の残差　モデルから算出される相関係数とデータから算出される相関係数の残差を求めます。
    • 修正指数　モデル適合度の向上につながりそうな修正候補を指数として示します。
  • グラフ
    • パス図　モデルのパス図を作成します。

モデルの事後修正

今回のサンプルデータではモデルに十分な適合度がありましたが，実際の分析場面では適合度が十分とはいえない結果になる場合もあるでしょう。その場合，モデルのどの部分に問題があるのかを調べることで，モデルの適合度を向上させられることがあります。

相関行列の残差

そのための参考指標の1つが，モデルから算出される観測変数間の相関係数と，実際のデータにおける観測変数間の相関係数の間の残差です。相関係数の残差を算出するには，「相関行列の残差」の部分にチェックを入れます。またその際，「これ以上の値を強調」に指定されている数値より大きな絶対値の部分が赤色の文字で強調表示されます（図9.75）。

相関行列の残差

図9.75: 相関行列の残差

この相関係数の残差に大きな値（たとえば0.1を超えるようなもの）がある場合には，分析モデルではその関係がうまく説明できていないということになります。そうした部分が特定の変数（表の列または行）に集中しているようであれば，その変数を分析から除外してみたり，モデルにおけるその変数の扱いを修正したりすることによってモデルの適合度が向上するかもしれません。

修正指標

また，「修正指数」にチェックを入れると，分析に使用したモデルには含まれていない関係（パス）について，それらを加えたときにモデル適合度がどの程度向上するかを示す修正指数が算出されます。jamoviの初期設定では，この修正指数が3を超える部分が赤色で強調されるようになっていますが，この値は「これ以上の値を強調」の数値を指定することによって変更可能です。

今回の分析結果について修正指数を算出してみると，図9.76のような結果になります。

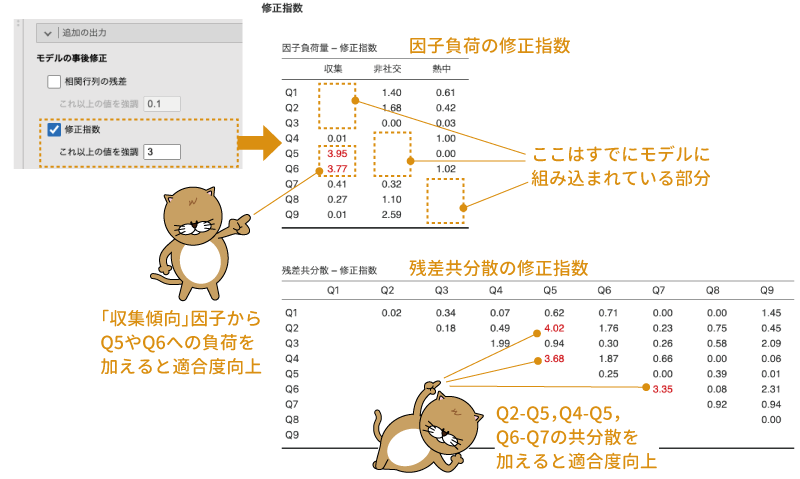
モデル修正指数

図9.76: モデル修正指数

この結果の1つ目の表から，「収集傾向」の因子で「Q5」と「Q6」の部分が赤になっていますから，現在のモデルに対してこれらのパス（「収集傾向」因子から「Q5」と「Q6」への因子負荷）をモデルに追加すると，さらにモデルの適合度が向上する可能性が高いということがわかります。

2つ目の表は残差共分散に関する修正指数です。今回のこの結果は，ここで赤字になっている部分，たとえば「Q2」と「Q5」の間で残差共分散を算出するようにモデルを修正するとモデル適合度が向上する可能性が高いということを示しています。

ただし，これらの数値はあくまでも「計算上，ここにパスを追加すると適合度があがる可能性がある」というものであって，そのようなパスが理解可能なものかどうかまでは保証されません。これらの指数にそって闇雲にモデルに修正を加えていくと，最終的に解釈不能なモデルになってしまう可能性が高くなります。モデルに修正を加える場合には，その修正が理解可能なものかどうかをよく考えるようにしてください。

そもそも，確認的因子分析はすでにある仮説モデルでデータをうまく説明できるかどうかを確認することを目的とした分析です。分析結果が思わしくなかったからといって，データに合わせて大幅に探索的にモデルを修正していくのは決して好ましいとはいえないでしょう。モデルの修正は，元の仮説で想定される範囲を超えない程度に留めておくことが重要です。

グラフ

なお，モデルに複数の修正を加えた場合，そのままではそのモデルがどのような形になっているのかを把握することが困難になっていきます。その場合，グラフの部分にある「パス図」にチェックを入れて，モデルを図示してみるとよいでしょう。「グラフ」の項目にチェックを入れると，図9.77のように各因子と観測変数の関係，因子間の相関，残差間の相関を図示してくれます。

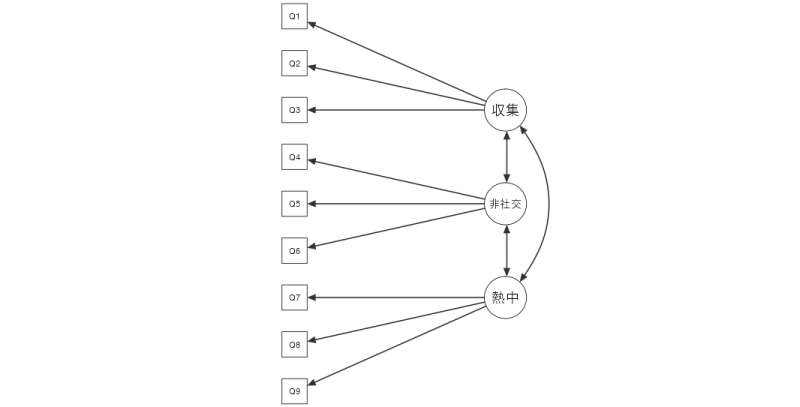
モデルのパス図

図9.77: モデルのパス図

なお，今回の分析ではモデルの修正は行っていませんので，ここに示されるパス図は，縦横の向きは違うだけで分析前に示したパス図と同じものになっています。