7.6 順序従属変数
今度は次のサンプルデータ(regression_data05.omv)について考えてみましょう。このデータには,起床時の気分,睡眠時間,日中ストレス,日中の歩数が200件分記録されています(図7.91)。
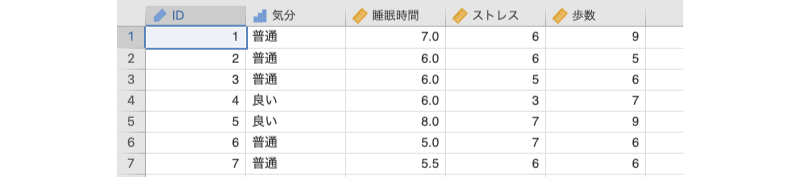
図7.92: サンプルデータ
ID対象者ID気分起床時の気分(悪い,普通,良い)睡眠時間前日の睡眠時間(単位:時間)ストレス日中ストレス度(1:弱〜10:強)歩数1日の歩数(単位:千歩)
このデータから,起床時の気分(目覚めの良さ)に影響する要因について次の回帰モデルで分析したいとしましょう。
\[ \text{気分} = b_0 + b_1 \times \text{睡眠時間} + b_2 \times \text{ストレス} + b_3 \times \text{歩数} \]
先ほど多項ロジスティック回帰分析で使用したデータと同様に,今回も従属変数である「気分」の値は「悪い」,「普通」,「良い」の3種類です。ですので,先ほどと同様にして多項ロジスティック回帰分析を用いてもよいかもしれません。その場合,分析においては起床時の気分を名義型変数として扱うことになります。ですが,起床時の気分の「悪い」,「普通」,「良い」の3つ値にははっきりした順序性があり,これは順序型変数といえますので,ここではその順序性を損なわいよう,順序ロジスティック回帰分析と呼ばれる手法を用いて分析したいと思います。
7.6.1 考え方
多項ロジスティック回帰では,従属変数の値のうち1つを基準レベルとし,それに対して他の値との間でロジスティック回帰モデルを作成して分析を行いました。順序ロジスティック回帰分析もそれとよく似た形で分析を行うのですが,従属変数の値がもつ順序性を考慮して,次のような形でモデルを作成します。
従属変数の値が「悪い」または「普通・良い」のロジスティック回帰モデル
\[ \log\left(\displaystyle\frac{p(\text{普通・良い})}{p(\text{悪い})}\right) = b_{10} + b_1 \times \text{睡眠時間} + b_2 \times \text{ストレス} + b_3 \times \text{運動} \]
従属変数の値が「悪い・普通」または「良い」のロジスティック回帰モデル
\[ \log\left(\displaystyle\frac{p(\text{良い})}{p(\text{悪い・普通})}\right) = b_{20} + b_1 \times \text{睡眠時間} + b_2 \times \text{ストレス} + b_3 \times \text{運動} \]
つまり,「悪い(1)」,「普通(2)」,「良い(3)」の3段階を,「1 vs. 2・3」,「1・2 vs. 3」のように,ある順序未満とそれ以上という形に2分してロジスティック回帰モデルを作成するのです。もし従属変数の値が3段階でなく4段階であれば,その場合のロジスティック回帰モデルは「1 vs. 2・3・4」,「1・2 vs. 3・4」,「1・2・3 vs. 4」というように,3つのロジスティック回帰モデルを用いて分析することになります。
このとき,順序ロジスティックモデルでは,偏回帰係数(\(b_1\),\(b_2\),\(b_3\))はすべてのモデルで同じであり,それぞれのモデルで異なるのは切片(\(b_{10}\),\(b_{20}\))と残差のみであるという仮定のもとで回帰係数の算出を行います。このような形で計算を行うロジスティック回帰モデルは累積ロジスティック回帰モデルとも呼ばれます。
7.6.2 分析手順
順序ロジスティック回帰は,「 回帰分析」の一番下にある「順序従属変数」を選択して実行します(図7.93)。
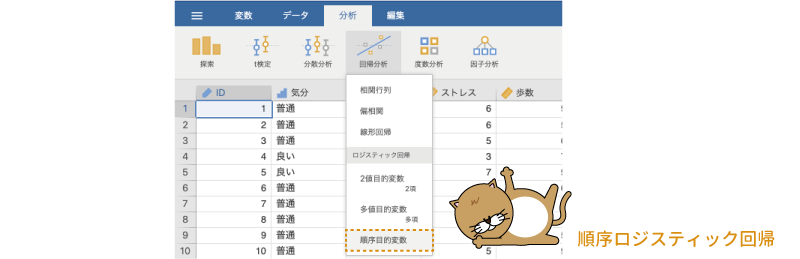
図7.93: 順序ロジスティック回帰分析の実行
順序ロジスティック回帰の設定画面は図7.94のようになっています。
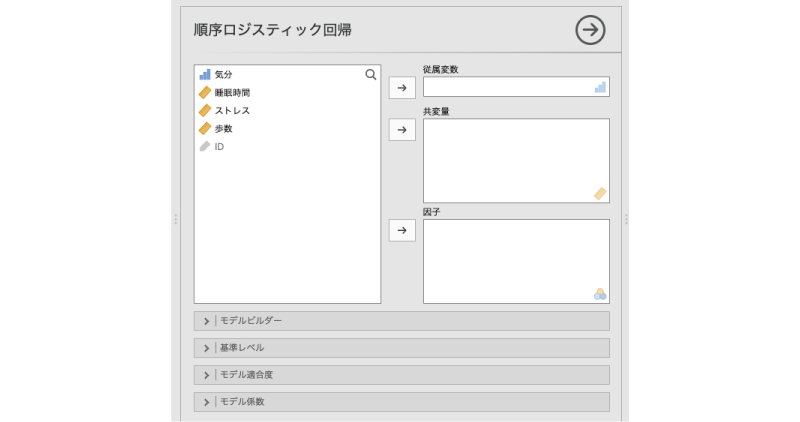
図7.94: 順序ロジスティック回帰分析の設定画面
見てわかるように,設定画面の構成や項目は他のロジスティック回帰とほとんど同じです。そのため,ここでは順序ロジスティック回帰に固有の部分を中心に説明していくことにします。それ以外の設定項目については,2項ロジスティック回帰や多項ロジスティック回帰のところを参照してください。
設定画面の「従属変数」に従属変数(「気分」)を,「共変量」に連続型の予測変数を設定すれば分析の基本設定は終了です(図7.95)。名義型の予測変数がある場合は,それらは「因子」に設定してください。
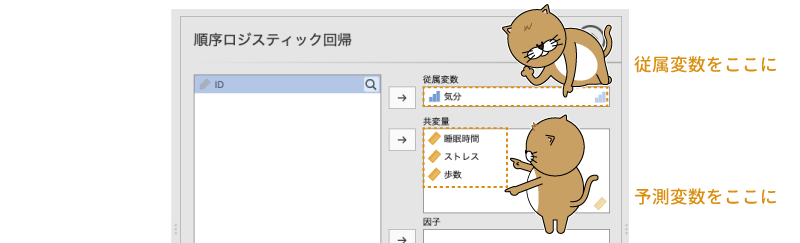
図7.95: 順序ロジスティック回帰分析の分析設定
7.6.3 分析結果
順序ロジスティック回帰の結果は,図7.96のような形で表示されます。
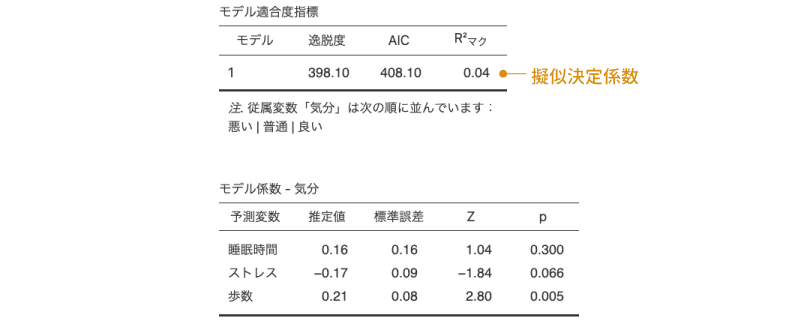
図7.96: 順序ロジスティック回帰分析の結果
図7.96を見てわかるように,モデル適合度の表とモデル係数の表の形式や内容も,2項ロジスティック回帰や多項ロジスティック回帰の場合とほぼ同じです。モデル適合度の表には逸脱度や擬似決定係数が,モデル係数の表には各予測変数の回帰係数の推定値や,その係数が0でないかどうかのz検定の結果が示されます。この結果をみると,起床時の気分に有意に影響を与えているのは「歩数」のみです。「歩数」の回帰係数はプラスの値ですので,日中たくさん歩いた場合ほど起床時の気分が良くなるといえそうです。
モデルの閾値
順序ロジスティック回帰では,多項ロジスティック回帰の場合と同様に複数のロジスティック回帰モデルを用いて分析を行っていますが,多項ロジスティック回帰のように複数の回帰係数が表示されることはありません。考え方のところでも説明したように,順序ロジスティック回帰では,すべてのモデルで偏回帰係数が共通であるという前提で分析を行うからです。
また,順序ロジスティック回帰のモデル係数の表には切片の推定値が含まれていません。この分析における切片の推定値を表示させるには,分析設定画面のの「閾値」ところで「モデルの閾値」にチェックを入れます(図7.97)。
図7.97: モデルの切片を表示させる
すると,図7.98のように各モデルの切片の値のみをまとめた表が表示されます。

図7.98: 順序ロジスティック回帰モデルの切片
これらの結果を元にして,最初に示した回帰モデルに切片と係数の値を示すと次のようになります。
\[\begin{eqnarray*} \small{\log\left(\displaystyle\frac{p(\text{普通・良い})}{p(\text{悪い})}\right)} & = & \small{0.28 + 0.16 \times \text{睡眠時間} + (-0.17) \times \text{ストレス} + 0.21 \times \text{歩数}}\\ \small{\log\left(\displaystyle\frac{p(\text{良い})}{p(\text{悪い・普通})}\right)} & = & \small{2.64 + 0.16 \times \text{睡眠時間} + (-0.17) \times \text{ストレス} + 0.21 \times \text{歩数}} \end{eqnarray*}\]
また,各モデルの閾値(切片)の推定値についての検定では,「普通 | 良い」は有意ですが「悪い | 普通」は有意ではありませんでした。これは,「普通 | 良い」つまり「普通以下(悪い・普通)」と「良い」の区別はできていても,「悪い」と「普通以上(普通・良い)」の区別はできていないということです。
これらの結果を総合すると,日中にたくさん歩くことは起床時の気分の良さにつながるけれども,歩かなかったからといって起床時の気分が悪くなるわけではないということになります。