9.2 主成分分析
ここからは,数学的にデータを縮約する方法について見ていきましょう。
データの縮約とは,たくさんあるデータを類似性などを基準に整理し,それらをより少数の意味あるまとまりとして集約することをいいます。質問紙調査などによる調査研究では,データとして何十種類もの質問文に対する回答値が得られるのが普通ですし,それ以外の場合にも,関心のある事象に関連した指標をできる限り幅広く集めて分析を行おうとすると,分析に使用する変数の種類は膨大になってしまいます。そこで,そのような場合には,多変量解析によって,そうした複雑なデータを,できるだけ元の情報を損なわないようにしながら可能な限り単純化し,理解可能なものに分類,整理しようとするわけです。
このデータ縮約の方法の1つとして,主成分分析(PCA)があります。主成分分析では,次に説明するような考え方で複数の変数がもつ情報を統合し,より少ない数の合成変数に集約するということを行います。
9.2.1 考え方
ここでは次のサンプルデータ(factor_data02.omv)を用いて主成分分析の基本的な考え方を見ておきましょう。このデータは,ある大学の学生男女計250人を対象に,食堂で提供されている代表的なメニュー6種類に対する満足度を「1:とても不満」から「7:非常に満足」までの7段階でたずねた結果です(図9.14)。このデータを用い,この食堂で提供されているメニューに対する総合的な満足度について分析したいと思います。
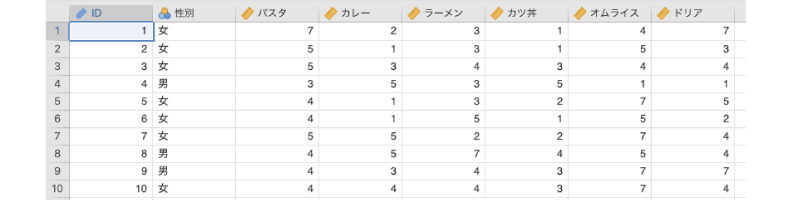
図9.14: サンプルデータ
ID回答者のID性別回答者の性別パスタパスタに対する満足度カレーカレーに対する満足感ラーメンラーメンに対する満足感カツ丼カツ丼に対する満足感オムライスオムライスに対する満足感ドリアドリアに対する満足感
このデータには全部で6種類のメニューに対する満足度が記録されているわけですが,これらを個別に分析した場合,個別のメニューに対する満足度の傾向は見ることができても,メニュー全体に対する全体的な満足度についてはわかりません。メニューに対する全体的満足度について知るには,これら6つのメニューに対する満足度を,なんらかの形で統合する必要があります。それにはどうすればよいのでしょうか。ここでは話を単純にするために,2つの変数を1つに統合する場合を例に見ていきます。
ここに,r=0.8の正の相関関係にある2つの変数があるとします。相関係数が0.8の変数の値を散布図に示すと,おおよそ図9.15のようなものになります。
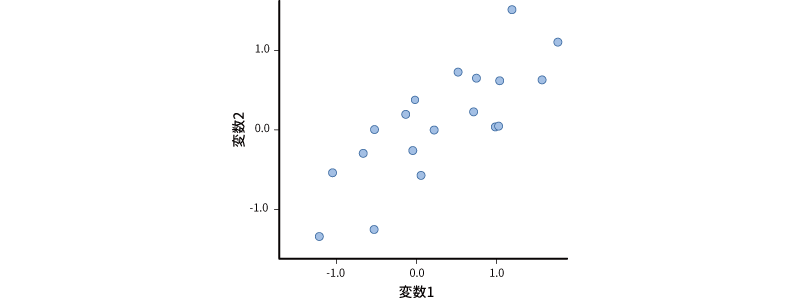
図9.15: 相関r=0.8の2変数の散布図
この散布図は,2つの変数が持っている情報を,変数1の軸(横軸)と変数2の軸(縦軸)の2つの軸で表現される平面上の点として表現したものです。そして,この2つの変数がもつ情報を1つに集約するということは,この2つの軸で表現されている情報を1つの軸だけで表現するということになるのです。
ここで,たとえばこの散布図に示されたデータの情報を横軸のみで表現した場合について考えてみましょう。縦軸のみで表現するということは,縦軸の値(変数2)は無視するということですので,ここでは変数2の値をすべて0として散布図上に示しなおします(図9.16)。
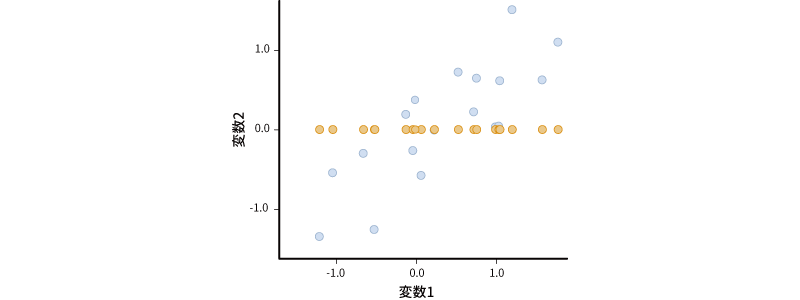
図9.16: データを横軸に集約した場合の散布図
すると,散布図上の点が横一列に並びました。1つの軸で表現するということは,このようにデータの点が一直線上に並ぶようにするということなのです。
ただし,これでは単に変数2がもつ情報(y軸がもつ情報)を捨てているだけですので,2つの軸がもつ情報を1つの軸に集約したことによって,多くの情報が失われてしまいます(図9.17)。
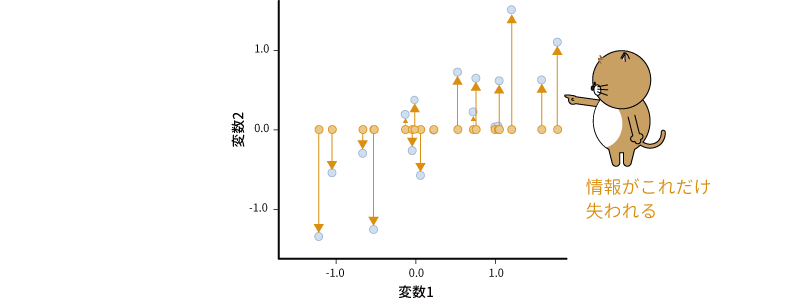
図9.17: 集約による情報の損失
そこで,もう少し工夫をしてみましょう。このように2変数間に正の相関がある場合,その散布図は右肩上がりの楕円形の形になります。その楕円の中央を,楕円の長いほうの軸にそって貫通するような直線を引き,その直線を軸として散布図上の情報を集約させてみます(図9.18)。
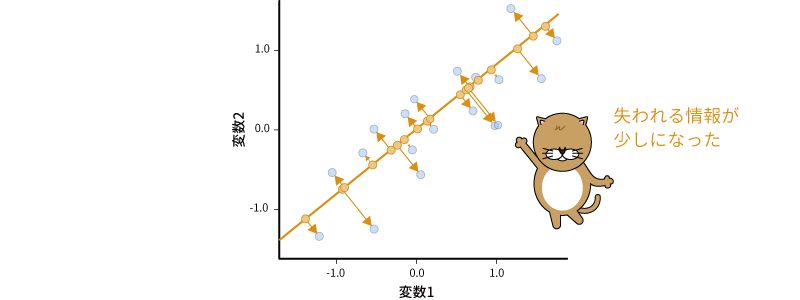
図9.18: 情報の損失が少ない軸に集約
すると,先ほどの場合よりも失われる情報の量がずっと少なくなりました。このような形で情報を集約できれば,2つの軸で表現される情報を1つの軸で表現したとしても,もとの情報が多く損なわれてしまうということがありません。
主成分分析では,このようにしてデータのもつ情報ができるだけ失われないようにしながら,もとのデータよりも少ない軸を用いてデータを表現しなおすのです。
このとき,この情報を集約する軸は,次のような式によって表現されます。
\[ z = a_1 \times \text{変数}_1 + a_2 \times \text{変数}_2 + \cdots + a_n \times \text{変数}_n \]
先ほどの2変数の例の場合,情報を集約する軸の式は,\(z=a_1\times\text{変数}_1+a_2\times\text{変数}_2\) となります。つまり,2つの変数の値になんらかの重みづけを行ったうえで合計するという形で合成得点を作成するのです。そして分析においては,このような変換によって失われる情報量が最小となるように,この式における重みづけの部分の値を決定します。
なお,この式は一見すると回帰分析で用いられる回帰式によく似ていますが,式の左辺にあるのが分析に使用する変数ではなく,合成得点zになっているという点に注意してください。この式によって算出される左辺zの値は主成分得点と呼ばれます。
それでは,jamoviにおける主成分分析の手順を見ていきましょう。なお,jamoviの主成分分析は,多変量解析の教科書の多くで説明されている主成分分析の形ではなく,かなり因子分析寄りの分析手法および結果表示になっています。この後の説明では,主成分分析と因子分析の違いを明確にするためにも,できるだけ統計法の教科書に近い形での結果になるように設定を行いながら分析を進めていきたいと思います。
また,主成分分析には分散共分散行列4を用いる場合と相関行列を用いる場合とがあり,その両者で算出される固有ベクトルの値が異なります。jamoviでは,相関行列を用いた主成分分析が実行されます。
9.2.2 基本手順
主成分分析を実行するには,分析タブの「 因子分析」から「主成分分析」を選択します(図9.19)。
図9.19: 主成分分析の実行
すると,図9.20のような設定画面が表示されます。
図9.20: 主成分分析の設定画面
- 方法
- 回転法 主成分の回転法を設定します。
- 主成分数
- 平行分析に基づく 平行分析の結果をもとに主成分の個数を決定します。
- 固有値に基づく 固有値の大きさが指定値以上の主成分を採用します。
- 数値指定 主成分の個数を直接指定します。
- 前提チェック
- バートレットの球面性検定 バートレット(Bartlett)の球面性検定を実施します。
- KMO標本妥当性指標 標本妥当性指標(MSA)を算出します。
- 因子負荷
- これ未満の負荷量を隠す 絶対値の小さい負荷量を非表示にします。
- 負荷量順に並び替え 負荷量の絶対値が大きい順に変数を並び替えて表示します。
- 追加の出力
- 主成分の要約量 各主成分について要約量を算出します。
- 主成分の相関 各主成分の間の相関を算出します。
- 回転前の固有値 回転前の固有値とその寄与率,累積寄与率を算出します。
- スクリープロット スクリープロットを表示します。
- 分析結果を新たな変数に保存します。
この設定画面で,主成分分析の対象となる変数(「パスタ」から「ドリア」まで)を「変数」欄に移動します(図9.21)。
図9.21: 分析対象の変数を設定
これで基本的な分析手順は終わりです。ただし,主成分分析の結果は設定によって大きく変わりますので,結果の見方についての説明に入る前に,いくつかの設定項目について説明しておきたいと思います。
回転法
主成分分析の目的は,たくさんの変数をできるだけ少数の変数に集約することにあります。そのため,まずは分析に使用した変数全体が持っている情報を1つの軸に集約し,そこで拾いきれなかった情報を2つ目,3つ目の軸に集約していくというのがもともとの考え方です。
しかし,情報の損失を最小限にすることだけを目的として軸を設定した場合,その軸が一体何を表しているのかが解釈困難になる場合もあります。心理学における研究の場合,多数ある変数を少数の軸に集約するだけでなく,それらの軸に対する解釈も重要な関心対象であることがよくあります。そのため,主成分分析の結果を解釈しやすくすることを目的として,分析で得られた軸に対して「回転」と呼ばれる操作を行う場合があります。
jamoviの主成分分析では,分析設定画面の「方法」にある「回転法」でこの回転方法についての設定ができるようになっており,初期設定値では,回転方法は「バリマックス」が指定されています。ここでは,この設定値を「なし」に設定してください(図9.22)。

図9.22: 主成分の回転法を「なし」に設定
いわゆる「総合得点」を算出したい場合には,回転は「なし」にしておきます。そうすることによって,軸を回転する前の主成分分析結果を得ることができるからです。なお,多変量解析の教科書の多くは,主成分分析では回転を行っていません。
「総合得点」を算出することよりも集約した軸の解釈が主な目的の場合には,適切な回転方法を選んで指定します。軸の回転方法については因子分析のところで説明するため,ここでは省略します。
主成分数
主成分分析では,計算上は元の変数と同じ数だけ主成分が抽出されます。しかし,変数が多いからデータがもつ情報を少数の軸に縮約しようとしているのに,元の変数と同じ個数だけ主成分を抽出したのでは意味がありません。そこで実際の分析では,抽出された中から適切な個数の主成分だけを選んで使用するのですが,その際,主成分の「適切な個数」については,いくつかの判断方法があります。
jamoviの「主成分数」の設定項目には,次の3種類が用意されています。

図9.23: 採用する主成分の個数の設定
- 平行分析に基づく
- 固有値に基づく
- 数値指定
ここでは,これら3つの項目を中心に,適切な主成分の個数を判断する方法について見ていきましょう。
平行分析に基づく
1つ目の「平行分析に基づく」では,平行分析と呼ばれる手法を用いて最適と考えられる主成分の個数を決定します。jamoviでは,この方法が初期設定値になっています。
この方法では,まずコンピューターを用いて,分析データと変数の個数が同じで標本サイズも同じであるランダムなデータを複数発生させます。そして,それらを用いて主成分分析を行った場合の平均的な結果と,実際のデータを主成分分析した場合の結果を比較し,ランダムなデータの場合よりも固有値が大きい主成分を採用するという方法をとります。
さて,この「固有値」とは一体何なのでしょうか。これをきちんと説明するのは非常に難しいので,ここでは大まかなイメージをつかんでおくことにしましょう。
先ほど,主成分分析の考え方のところでは,変数が2つの場合を例にとって説明をしました。変数が2つの場合,それらの変数がもつ情報は2つの軸で構成される平面上に表現することができます。もしこれが3つの変数の場合であれば,それらの変数がもつ情報は3つの軸で構成される3次元空間上に表現されることになります。
今回のサンプルデータでは変数の数は6個ですので,これら6つの変数がもつ情報は,6次元の空間(これがどのようなものかを図示することもイメージすることも不可能ですが)に表現されることになるわけです。そして主成分分析では,それらn次元の空間に表現された情報を,できるだけ情報の損失がないような形で集約できる軸を探していきます。
その際,その軸がどの方向を向いているのかを表した値が,先ほどの主成分得点の式における係数の部分です。2変数の場合には,主成分得点の式は「\(z=a_1\times\text{変数}_1+a_2\times\text{変数}_2\)」という形になりますが,これはこの軸が,グラフの原点(横軸・縦軸ともに0)と,横軸の座標が\(a_1\),縦軸の座標が\(a_2\)の点(\([{a_1}\ \ {a_2}]\))を通る直線であることを意味しています。変数が3つの場合にも,主成分の軸はやはり原点(\([0\ \ 0\ \ 0]\))と主成分得点の各係数を座標要素とする3次元空間中の点\([{a_1}\ \ {a_2}\ \ {a_3}]\)を通る直線になります(図9.24)。
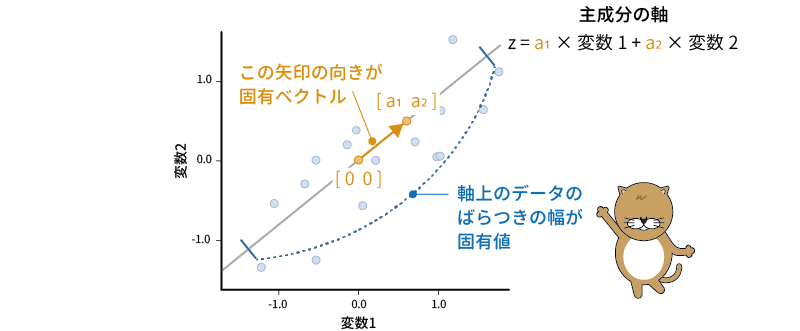
図9.24: 固有ベクトルと固有値
このとき,この主成分得点の式の係数で表現される\([{a_1\ \ a_2}]\)や\([{a_1\ \ a_2\ \ a_3}]\)は,数学的には分析対象データの相関行列(または分散共分散行列)の固有ベクトルと呼ばれるものになります。そして,その固有ベクトルにそった直線上にデータがどれだけ集約できているのか(その軸でどれだけのばらつきを表現できているか)を数値化したものが固有値です5。
なお,「平行分析に基づく」を選択した状態で「追加の出力」にある「スクリープロット」にチェックを入れると,平行分析におけるランダムなデータと実際のデータの固有値の変化を見ることができます(図9.25)。
図9.25: 平行分析のスクリープロット
固有値に基づく
2つ目の「固有値に基づく」も非常によく用いられる方法です。一般に,この方法では「固有値が1以上」(これは一般にカイザー基準と呼ばれます)の主成分を採用します。SASやSPSSなどの統計ソフトでは,この基準が標準として設定されており,分析で算出される固有値の値が1を超える主成分の情報のみが結果に表示されます。
主成分分析で主成分の個数を決める基準として用いられるのはデータの相関行列についての固有値ですが,この値はその主成分に「変数何個分」の情報が集約されているかという形で解釈することができます。つまり,「固有値1以上」というのは,最低でも変数1個分の情報を持っているような主成分だけを採用するということなのです。この方法を用いる場合には,「固有値に基づく」を選択して「固有値の最小基準値」を「1」に設定します。
数値指定
それ以外の方法で主成分の個数を判断した場合には,その個数を「数値指定」に指定することで,指定した個数の主成分を抽出することができます。
固有値の大きさや平行分析以外の方法で主成分の個数を判断するものとしては,たとえばスクリープロットと呼ばれる方法があります。
主成分分析の主成分は,最初のものほど固有値が大きく,2番目の主成分,3番目の主成分と,順番が後ろの主成分になるにつれて固有値は小さくなっていきます。そしてこの各主成分の固有値の大きさをグラフに示したものがスクリープロットで,この方法では,グラフ上で固有値の変化が小さくなる手前までの主成分を採用するという方法をとります。
スクリープロットを利用して主成分の個数を判断したい場合には,この「数値指定」を選択した状態で,「追加の出力」にある「スクリープロット」にチェックを入れてスクリープロットを作成します(図9.26)。
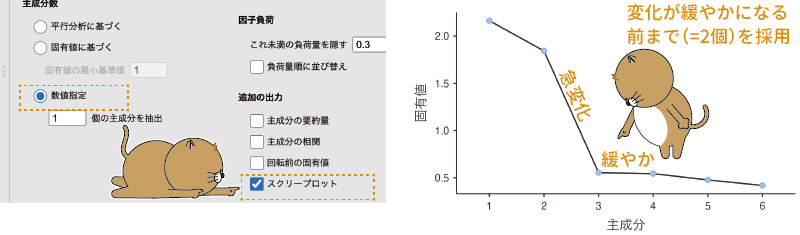
図9.26: スクリープロットを用いた判断
今回のデータでは,3つ目の主成分以降は固有値の変化がほとんどありませんので,その手前の2つ目までの主成分を採用すると判断するわけです。そして,そのように判断したら,その主成分の個数(「2」)を「数値指定」の数値入力欄に指定します。
その他の基準としては,「累積説明率が70〜80%以上」というものもあります。説明率(寄与率)とは,データ全体のうち,その主成分に集約されている部分の割合のことで,各主成分の説明率は,その主成分の固有値を分析に使用した変数の個数で割った値になります。この「累積説明率が70〜80%以上」という基準は,最初の主成分から順に2番目,3番目と主成分の説明率を合計していき,その合計値が0.7〜0.8以上になるところまでの主成分を採用するという方法です。
この方法を用いる場合には,「追加の出力」にある「回転前の固有値」にチェックを入れます(図9.27)。すると,各主成分の分散説明率と,その主成分およびその手前の主成分の説明率の合計値(累積%)の表が出力されますので,そこから判断した主成分の個数を「数値指定」の数値入力欄に指定します。
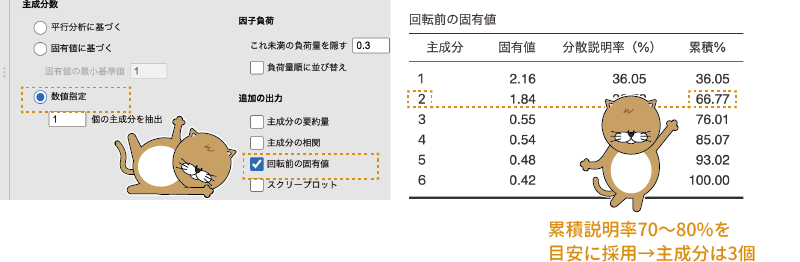
図9.27: 累積説明率を基準とする判断
なお,これらの基準は,どれも絶対的なものではなく,主成分の適切な個数を判断する際の目安にすぎません。「固有値1以上」という基準では,主成分の個数が多すぎたり少なすぎたりする場合があります。また,分析の目的にもよるでしょうが,「累積説明率70〜80%以上」という基準では,主成分の数が多くなりすぎる傾向があります。平行分析の場合にも,主成分の個数が少なめに判定されることがあるようです。そのため,これらの基準を参考にしながら,最終的には分析者の判断で適切と考えられる主成分の個数を決定することになります。
なお,今回のサンプルデータの分析では,主成分の個数は平行分析に基づいて決定することにしましょう。ここでは,「主成分数」は,初期設定値の「平行分析に基づく」にします。
因子負荷
「因子負荷」には,次の2つの項目が含まれています(図9.28)。

図9.28: 因子負荷の設定項目
- これ未満の負荷量を隠す 絶対値の小さい負荷量を非表示にします。
- 負荷量順に並び替え 負荷量の絶対値が大きい順に変数を並び替えて表示します。
これ未満の負荷量を隠す
1つ目の「これ未満の負荷量を隠す」の項目は,結果の表の中に絶対値が小さな負荷量を表示しないようにするための設定です。分析に使用する変数や主成分の数が多い場合,主成分とほとんど関連がない部分については数値を非表示にしてしまったほうが,主成分と各変数との関係を把握しやすくなります。そのため,jamoviの初期設定では,負荷量の絶対値が0.3未満の場合にその部分が非表示になるように設定されています。
今回の分析結果ではそのような値は1つもありませんでしたが,結果の表の中に数値が表示されていない部分がある場合には,それらの負荷量はここで設定されている基準値よりも小さいということです。
なお,分析の過程では確かに小さい負荷量は非表示のほうが見やすいかもしれませんが,レポートや論文に結果を報告する際には,それら小さな負荷量も含めて報告するほうがよいでしょう。その場合には,「これ未満の負荷量を隠す」の値を「0」にすることですべての負荷量を表示させることができます。
負荷量順に並び替え
この項目は,分析に使用した変数を負荷量の大きさの順に並び替えて表示させるかどうかについての設定です。分析に使用する変数が多い場合や,抽出した主成分の個数が多い場合などは,このチェックをオンにしておくと結果が見やすくなります。
今回の分析では,この設定はオフのままにしておきます。
追加の出力
「追加の出力」には,次の4つの項目が含まれています(図9.29)。

図9.29: 追加の出力
- 主成分の要約量 各主成分について要約量を算出します。
- 主成分の相関 各主成分の間の相関を算出します。
- 回転前の固有値 回転前の固有値とその寄与率,累積寄与率を算出します。
- スクリープロット スクリープロットを表示します。
主成分の要約
この項目は,抽出された主成分の固有値や寄与率についての情報を表示させるかどうかの設定です。この設定項目は,主成分に対して回転を行った場合にその回転後の主成分の情報を知りたい場合に使用します。主成分の回転を行わない場合は,この設定で表示される内容は「回転前の固有値」の表の一部とまったく同じですので,今回のサンプルデータを用いた分析ではここは設定の必要はありません。
主成分の相関
この項目は,主成分の間の相関係数を算出するための設定項目です。主成分に対して回転操作を行った場合には,その回転方法によって主成分の間に相関が見られることがあるのですが,主成分に対して回転を行わない場合,それぞれの主成分は互いに独立(相関0)になりますので,今回の分析ではここも設定の必要はありません。
回転前の固有値
主成分の数値指定のところで説明したように,「回転前の固有値」にチェックを入れると,抽出直後の各主成分の固有値と分散説明率(寄与率),そしてその主成分までの寄与率の合計(累積%)が表示されます。
スクリープロット
すでに平行分析や主成分の数値指定のところで説明したように,「スクリープロット」にチェックを入れると固有値のスクリープロット が作成されます。
なお,この「スクリープロット」の項目は,「主成分数」で3つのうちのどれが選択されているかによって少しずつ表示が異なります。「主成分数」で「平行分析に基づく」が選択されている場合には,分析データとランダムなデータについてのスクリープロットが1つのグラフに示されますが,ここが「固有値に基づく」になっている場合には,「固有値の最小基準値」で指定された位置に点線が示されます。また,「主成分数」が「数値指定」になっている場合には,固有値のみがグラフ上に示されます(図9.30)。
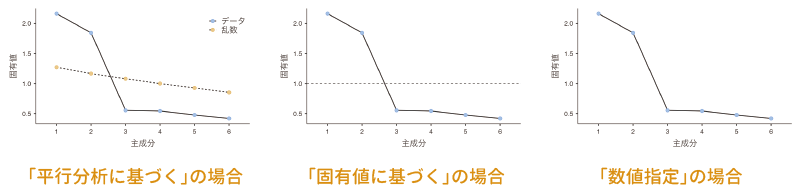
図9.30: スクリープロットのバリエーション
9.2.3 分析結果
主成分の個数は平行分析を基準に決定し,主成分の回転は行わないという設定で分析をすると,その結果は図9.31のようになります。
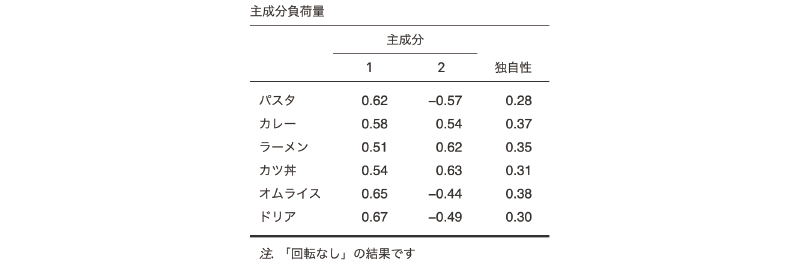
図9.31: 主成分分析の結果
この表の「主成分」の部分に示されているのは主成分負荷量と呼ばれる値で,これは各変数と主成分との間の相関関係を示しています。この値は,その主成分の固有値の平方根と固有ベクトルを掛け合わせることによって求められます。
回転を行わない主成分分析の場合,1つ目の主成分は全体を総合するような(総合得点的な)ものになることが多いのですが,今回の結果でも,第1主成分はどの変数の値とも0.5から0.7程度の正の相関関係にあり,メニュー全体に対する総合的な満足度を反映した軸といえるようなものになっています。つまり,この主成分の得点が高い人ほど全体的に満足度が高く,主成分得点が低い人ほど全体的に満足度が低い傾向にあるということです。
これに対し,第2主成分ではカレーとラーメン,カツ丼に対する負荷量がプラスになっており,それ以外がマイナスであることから,この主成分の得点が高い人ほどカレーやラーメンなどのいわゆる「がっつり」したにメニューに対する満足度が高く,この主成分の得点が低い人ほどパスタやオムライスなどの洋食メニューに対する満足度が高くなく傾向にあることがわかります。このことから,この第2主成分は,がっつり志向かどうかという,志向性の違いを表しているといえるでしょう。
結果の表の「独自性」の部分は,各変数がもつ情報のうち,この2つの主成分に集約しきれなかった情報の割合を示しています。この独自性の値に,たとえば0.8(80%)を超えるようなものが含まれている場合,その変数は主成分に情報がうまく集約できていないことを意味します。今回の分析結果では,どの変数も独自性は0.3前後ですので,2つの主成分に60%から70%程度の情報が集約できていることになります。これは分析結果としては十分な値でしょう。
9.2.4 分析の詳細設定
基本的な分析が終わりましたので,ここからは主成分分析のその他の設定項目について見ていきましょう。
前提チェック
他の分析手法と同様に,主成分分析にも分析のための全体となる条件がいくつか存在します。それらの条件が満たされているかどうかは,「前提チェック」に含まれる項目を用いて確認できます(図9.32)。

図9.32: 前提チェック
- バートレットの球面性検定 バートレットの球面性検定を実施します。
- KMO標本妥当性指標 標本妥当性指標(MSA)を算出します。
バートレットの球面性検定
この項目にチェックを入れると,バートレットの球面性検定と呼ばれる検定が実施されます。
主成分分析では,複数の変数で表現されている情報をより少数の主成分に集約するということを行うわけですが,その際,分析に使用する変数が互いにまったく無関係なものであると,それらを集約することができません。そこで,分析に使用するデータの中に主成分分析を適切に行えるだけの関連性が見られるかどうかを確かめるのが,このバートレットの球面性検定です。
この検定のチェックをオンにすると,図9.33のような結果が得られます。

図9.33: 球面性検定の結果
この検定は,「分析データの相関行列が単位行列である」という仮説に対して検定を行っています。単位行列というのは,相関行列の対角(同じ変数同士の相関係数の部分)が1で,それ以外の要素(相関係数)がすべて0である状態です。つまり,この検定結果が有意である場合,「少なくとも1組以上の変数間に0でない相関がある」ということになります。今回の分析データに対する検定結果は有意(p<.001)ですから,分析のための最低限の条件は満たしていることになります。
KMO標本妥当性指標
「KMO標本妥当性指標」の項目は,カイザー=マイヤー=オルキン(KMO)の標本妥当性指標(KMO標本妥当性指標またはKMO指標)と呼ばれる値の算出を行います(図9.34)。

図9.34: KMO標本妥当性指標
この値は,変数間の相関および偏相関の情報をもとに算出されたもので,分析データに主成分として集約可能な部分がありそうな程度を示しています。この値の大きさについての大まかな目安は表9.2のとおりです。
| KMOの値 | 解釈 |
|---|---|
| 0.9〜1.0 | 非常に高い |
| 0.8〜0.9 | 高い |
| 0.7〜0.8 | 許容レベル |
| 0.6〜0.7 | 疑わしい |
| 0.5〜0.6 | 低い |
| 0.0〜0.5 | 著しく低い |
この値はデータ全体と各変数それぞれについて算出されますが,主成分分析を実施するには,次の表のように全体のKMO指標が0.8以上であることが望ましく,少なくとも0.6以上である必要があるとされます。もし全体指標の値が小さい場合には,個別指標の値が小さな変数を分析から除外するなどの対応をとります。
今回のデータについてのKMO指標は0.69でやや低めですが,分析に適さないというほどではなさそうです。
9.2.5 保存
主成分分析では,各対象者について各主成分の主成分得点を算出し,それを別の分析に使用することが可能です。
主成分得点の保存はとても簡単で,分析設定画面のを展開して「主成分得点」にチェックを入れるだけです。この操作をしてからデータを確認すると,新たに「主成分得点1」と「主成分得点2」という変数が追加されていることがわかります(図9.35)。
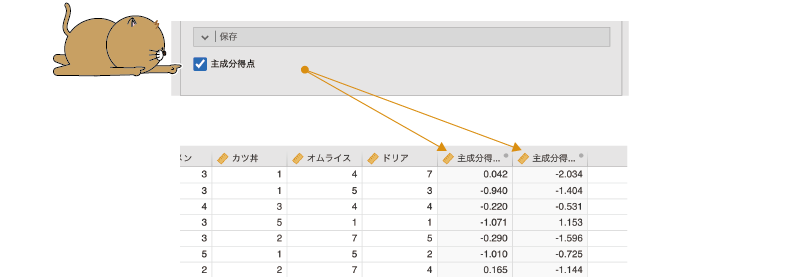
図9.35: 主成分得点の保存
今回の分析では2つの主成分を採用しましたので,それぞれについて主成分得点が算出されているのです。なお,主成分得点の算出方法は,分析の考え方のところで示した主成分分析の関係式に各回答者の回答値を代入することによって得られる値です。このデータの場合には,関係式は次のようになります。
\[ z = a_1 \times \text{パスタ} + a_2 \times \text{カレー} + \cdots + a_6 \times \text{ドリア} \]
そして,主成分1と主成分2のそれぞれについてこの式を用いて計算した結果が,各個人の主成分得点ということになります。
なお,この式における\(a_1\)や\(a_2\)は,主成分負荷量ではなく主成分分析で得られる固有ベクトルである点には注意が必要です。jamoviの分析結果では各主成分における固有ベクトルの値は表示されませんが,必要であれば主成分の負荷量を固有値の平方根で割ることによって求めることができます。
9.2.6 主成分得点を用いた分析
さて,分析で得た2つの主成分について主成分得点が求まりましたので,これらの値を使ってさらに別の分析を行ってみましょう。このサンプルデータには,食堂で提供されている代表メニューに対する満足度の他に,回答者の性別についての情報も含まれています。そこで,食堂で提供されているメニューに対する全体的な満足度やメニューに対する好みに男女差が見られるかどうかを見てみることにしましょう。
分析タブの「 t検定」から「対応なしt検定」を選択し,設定画面の「従属変数」の欄に先ほど算出した2つの主成分得点を,「グループ変数」の部分に「性別」を設定します(図9.36)。
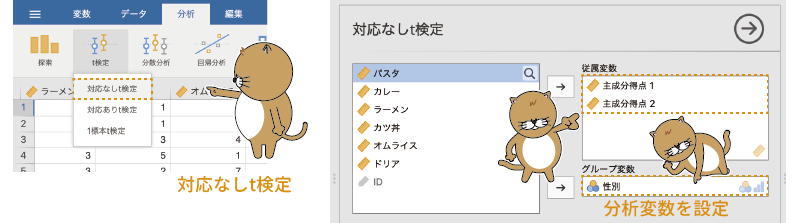
図9.36: 主成分得点を用いたt検定
また,男児それぞれにおける各主成分得点の平均値を見るために,「追加の統計量」で「記述統計」にもチェックを入れておきましょう(図9.37)。
図9.37: t検定と同時に記述統計量を算出
そして得られた結果が図9.38です。
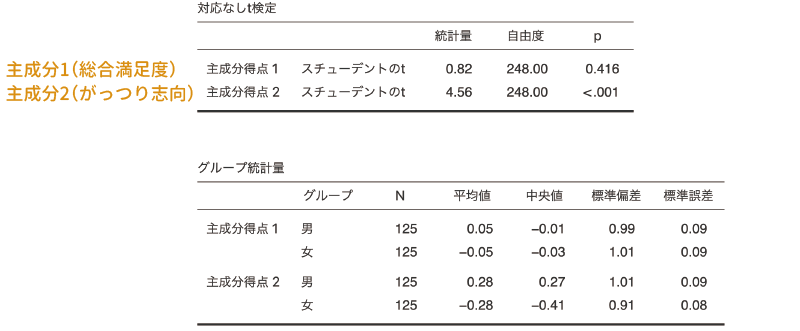
図9.38: 主成分得点のt検定の結果
この結果から,主成分1の主成分得点(食堂のメニューに対する全体的な満足度)は男女差が有意ではありませんが,主成分2の主成分得点(がっつり志向)においては男女差が有意になっています。また,算出された記述統計量からは,男性の主成分得点2の平均値は女性よりも高い値となっていますので,男性のほうがラーメンやカレー,カツ丼へといった「がっつり系」メニューへの志向が強く,女性はパスタやオムライス,ドリアなどの洋食メニューへの志向が強いことがわかります。