7.1 相関行列
「相関行列」の分析メニューでは,変数間の相関係数を算出することができます。相関係数は,2つの変数の間の関係を\(-\textsf{1}\)〜1の間で数値化した値です。2つの変数のうち一方の値が大きいほどもう一方の変数値も大きくなるというように,2つの変数の間に似た関係がある場合を正の相関といい,このような関係が強く見られるほど相関係数は1に近づきます。
これに対し,一方の変数の値が大きくなるほどもう一方の変数の値は小さくなるというような反対の関係が見られる場合を負の相関と呼び,このような関係が強く見られるほど相関係数は\(-\textsf{1}\)に近づきます。
また,2つの変数の間に正の相関も負相関も見られない場合には,相関係数は0になります。つまり相関係数は,数値の符号(\(+\cdot -\))で変数間の関係の向き(正・負)を,絶対値で関係の強度を示すのです(図7.2)。
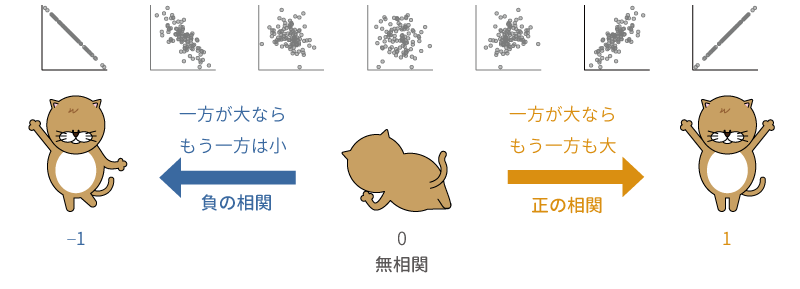
図7.2: 相関係数
相関係数の大きさについての解釈の目安としては,一般には表7.1のような基準がよく示されていますが,これらはあくまでも目安であり,相関係数がどの程度であれば相関が強いといえるかは研究対象などによっても異なります。
| 相関係数の絶対値 | 相関の強さ |
|---|---|
| 0.7 〜 1.0 | 強い相関 |
| 0.4 〜 0.7 | 中程度の相関 |
| 0.2 〜 0.4 | 弱い相関 |
| 0.0 〜 0.2 | ほぼ相関なし |
なお,この分析メニューの名前にある相関行列というのは,さまざまな変数ペアについて算出した相関係数を1つの表にまとめたもののことです。
7.1.1 分析手順
ここではまず,次のサンプルデータ(regression_data01.omv)を用いて相関分析の方法について見ていきましょう。このデータファイルには,100家族分の父親・母親・娘の身長データが格納されています(図7.3)。
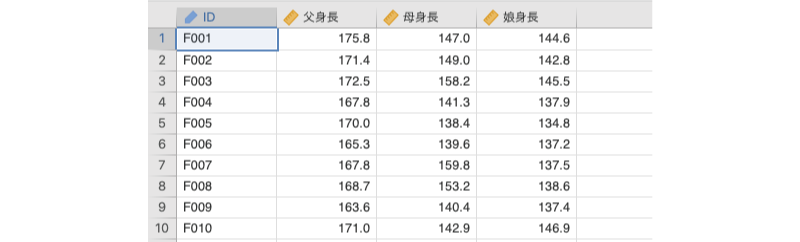
図7.3: サンプルデータ
ID対象家族のID父身長父親の身長(単位:cm)母身長母親の身長(単位:cm)娘身長娘の身長(単位:cm)
まずは基本的な分析手順からです。分析タブの「 回帰分析」から「相関行列」を選択してください(図7.4)。
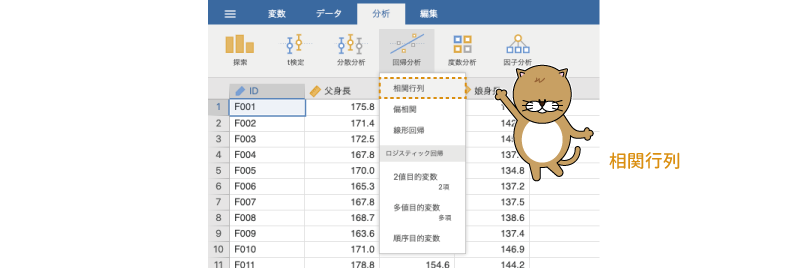
図7.4: 相関係数の算出
すると,図7.5のような画面が表示されます。ここでは,大まかな項目について見ておきましょう。
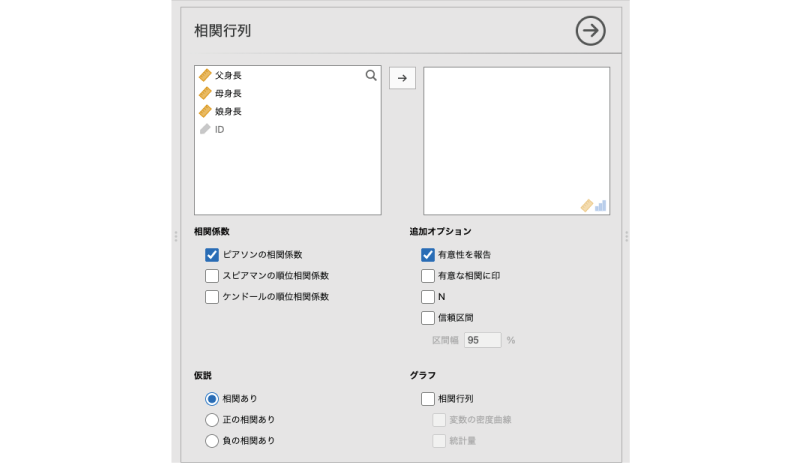
図7.5: 相関行列の設定画面
- 相関係数 算出する相関係数の種類を指定します。
- 仮説 有意性検定における仮説を指定します。
- 追加オプション 結果の表示方法についてのオプション設定です。
- グラフ 結果の図を作成します。
相関係数を算出するには,分析対象の変数を設定画面右側の欄に指定するだけです。ここでは,「ID」以外の3つの変数すべてを設定画面右側に移動してください(図7.6)。
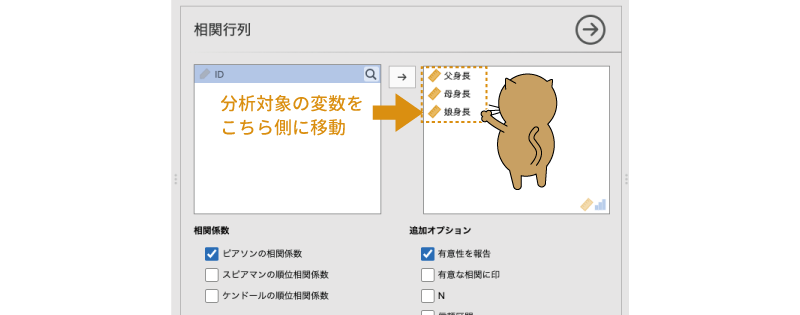
図7.6: 分析対象の変数を指定
すると,図7.7のような形で結果が表示されます。とくに設定しない限り,相関係数としてピアソンの相関係数(ピアソンの積率相関係数,r)が算出されます(図7.7)。
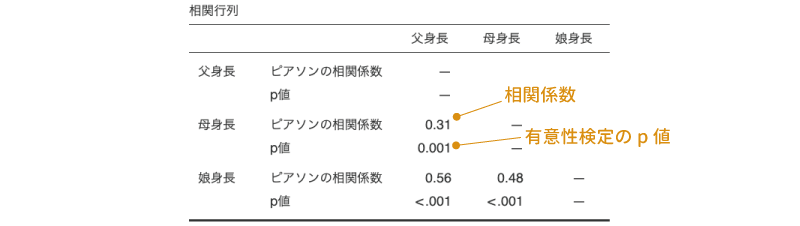
図7.7: 相関係数の算出結果
この表の「ピアソンの相関係数」という行に書かれている数値が相関係数です。ここでは,「父身長」と「母身長」の相関係数,「父身長」と「娘身長」の相関係数,「母身長」と「娘身長」の相関係数の3つの相関係数が1つの表にまとめられています。このように,複数の相関係数を1つの表にまとめたものが相関行列です。
なお,とくに分析設定を変更しないで相関係数を算出した場合,相関係数の下にその相関係数についての有意性検定の結果が示されます。このp値が有意水準より小さい場合に相関係数が統計的に有意であるとみなします。
7.1.2 分析設定
相関係数の算出は上記の手順だけで十分なことがほとんどでしょうが,ピアソンの相関係数以外の相関係数を算出したい場合や,結果の表示方法を変更したい場合などもあるでしょう。そこで,相関分析の各設定項目についても簡単に見ておくことにします。
相関係数
「相関係数」には次の項目が含まれています(図7.8)。
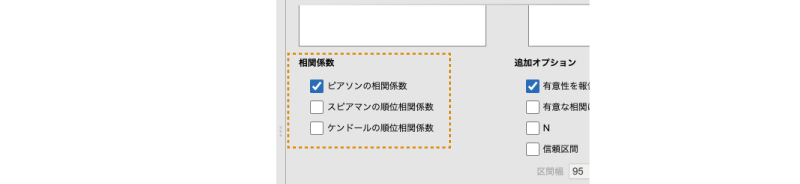
図7.8: 相関係数の設定項目
- ピアソンの相関係数 ピアソンの積率相関係数を算出します。
- スピアマンの順位相関係数 スピアマンの順位相関係数を算出します。
- ケンドールの順位相関係数 ケンドールの順位相関係数(τ-b)を算出します。
ピアソンの積率相関係数についてはすでに説明しましたので,ここでは残りの2つについて簡単に説明しておきます。
仮説
「仮説」には次の項目が含まれています(図7.9)。

図7.9: 有意性検定の設定項目
- 相関あり 相関係数が0でない場合に検定結果が有意になります(両側検定)
- 正の相関あり 相関係数が0より大きい場合に検定結果が有意になります(片側検定)
- 負の相関あり 相関係数が0より小さい場合に検定結果が有意になります(片側検定)
ここでは,相関係数の有意性検定において,両側検定を用いるか片側検定を用いるかの設定を行います。
追加オプション
「追加オプション」には次の項目が含まれています(図7.10)。
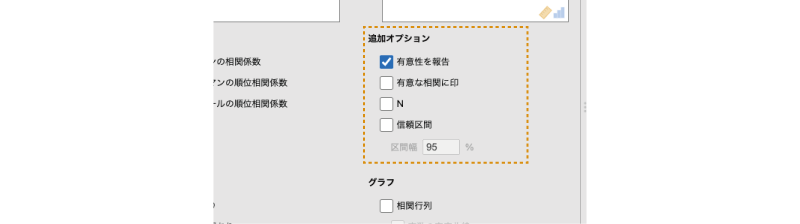
図7.10: 追加オプションの設定
- 有意性を報告 相関係数の下に,「p-value(有意性検定のp値)」を表示します。
- 有意な相関に印 統計的に有意な相関係数の右肩に「*」などの印をつけて示します。
- N 相関係数の算出対象となった標本サイズ(データペアの数)を示します。
- 信頼区間 相関係数の信頼区間を算出して示します。
有意性を報告
この項目のチェックがオンになっていると,相関係数の下に「相関係数が0である」という帰無仮説についての検定結果(p値)が表示されます。jamoviの初期設定では,この項目のチェックはオンになっています。
有意な相関に印
研究論文で相関行列を示す際には,すべての相関係数について有意性検定のp値を示すのではなく,5%や1%などの有意水準で統計的に有意な相関に「*」や「**」などの印をつけて示すのが一般的です。
このような,論文スタイルの相関行列を作成したい場合には,「有意性を報告」のチェックを外し,代わりに「有意な相関に印」にチェックを入れるとよいでしょう。すると,相関行列は図7.11のように論文でよく見かけるスタイルになります。
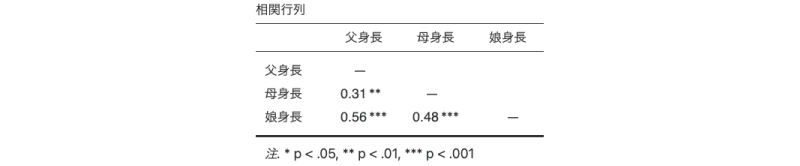
図7.11: 相関行列の見た目の変更
グラフ
「グラフ」には次の項目が含まれています(図7.12)。
図7.12: 作図設定
相関行列
ここで「相関行列」のチェックをオンにすると,各変数ペアの散布図が表示されます。この散布図には,回帰直線(「回帰分析」の項を参照)とその標準誤差も合わせて示されます。
統計量
最後の「統計量」は,図の中に相関係数を表示させるオプションです。このとき,図の中に示される相関係数は1種類のみで,複数の相関係数を算出するオプションが選択されている場合には,相関係数の設定項目で上にある相関係数が優先されます。
サンプルデータでピアソンの相関係数を算出し,作図のオプションをすべてオンにすると,結果は図7.13のようになります。
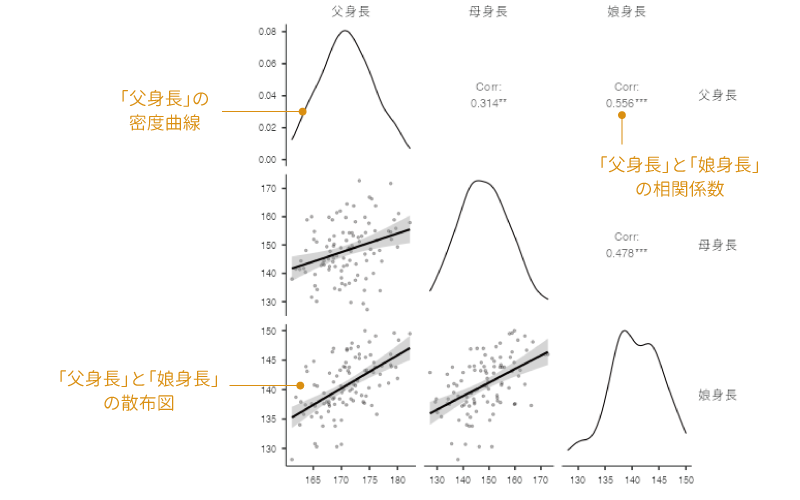
図7.13: 作図の例