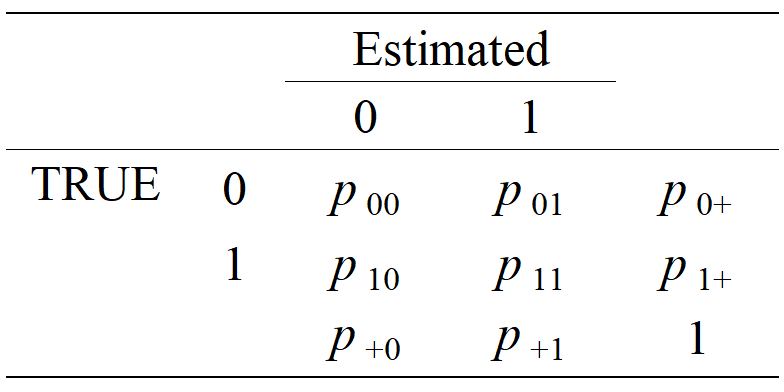
10.6 $2\times 2$ Contingency Table in Principle

The table below is similar to the Table 1 in Matthew and Sandip (2018), which plays a key role in estimating classification accuracy.

$p_{00}$ is the probability that a randomly selected student who does not master attribute $k$ is estimated to be absence of attribute $k$ given his or her responses $Y$.

$p_{11}$ is the probabbility that a randomy selected student who has attribute $k$ is estimated to master attribute $k$ given his or her responses $Y$.

More generally, we have

$P_{ab}= P(\alpha_k = a, \hat{\alpha}_k=b)$

This is for a single attribute and it is clear that the accuracy can be calculated as $p_{00}+p_{11}$.