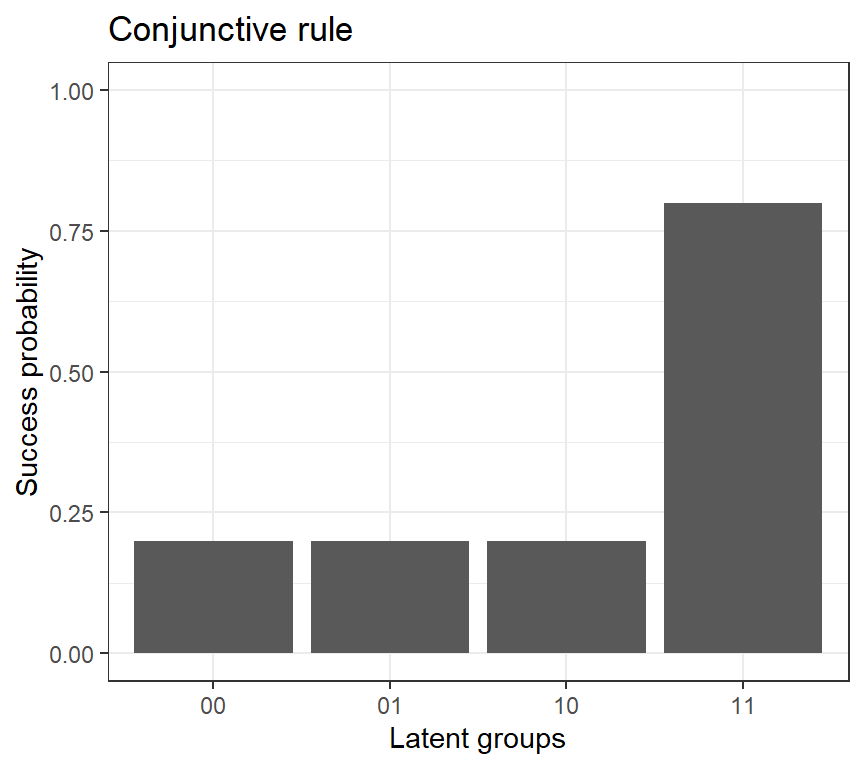
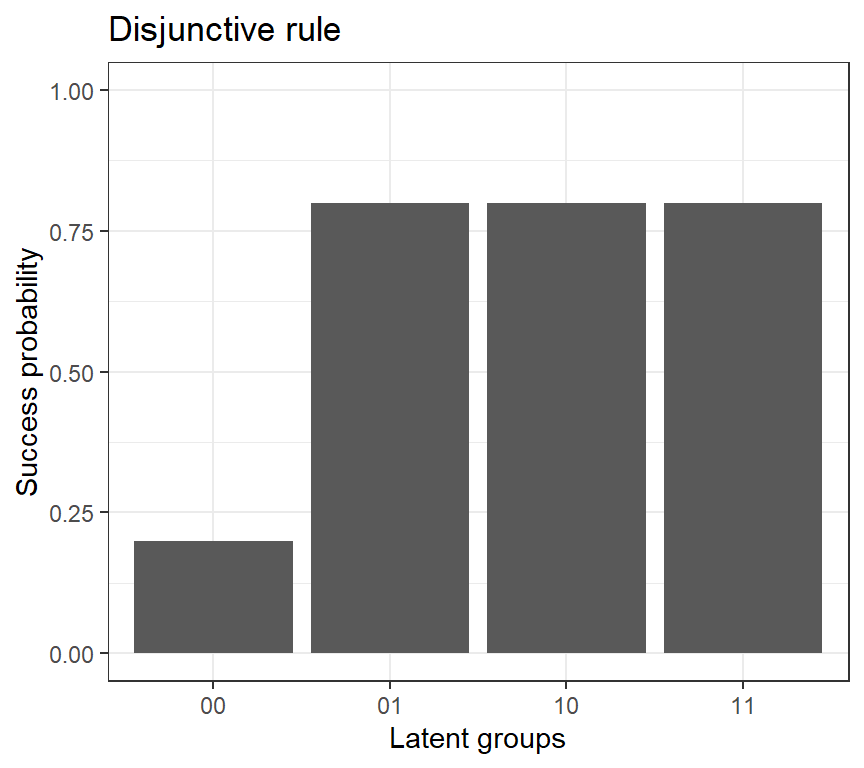
3.4 Condensation Rules

CDMs are models at item response level

The item response function, or the conditional probability of success on attribute profile, can be expressed as

\[ P(Y_{ij}=1|\alpha_c)= P(Y_{ij}=1|\alpha_{lj}^*)=f( \alpha_{lj}^*,\delta_j ) \]

To define the model, we need to specify the functional form \(f(\cdot)\)

In other words, we need to have some assumptions about how students use attributes to solve item \(j\) (i.e., condensation rule)

• Models are conjunctive if all the required attributes are necessary for successful completion of the item

• Models are compensatory if the absence of one attribute can be made up for by the presence of other attributes

• For most part, these two schemes of classifying CDMs are used interchangeably, specifically,

• conjunctive ≈ non-compensatory

• disjunctive ≈ compensatory

• Depending on how the terms are defined, the two classification schemes may not be identical