3.5 The DINA model
Stands for the deterministic input, noisy “and” gate model (Haertel, 1989; Junker & Sijtsma, 2001)
A conjunctive model: Students are not expected to answer an item correctly unless they master all required attributes
Item \(j\) splits the examinees in the different latent classes into groups:
those who have all the required attributes \((η_{jl} = 1)\) and
those who lack at least one of the required attributes \((η_{jl} = 0)\)
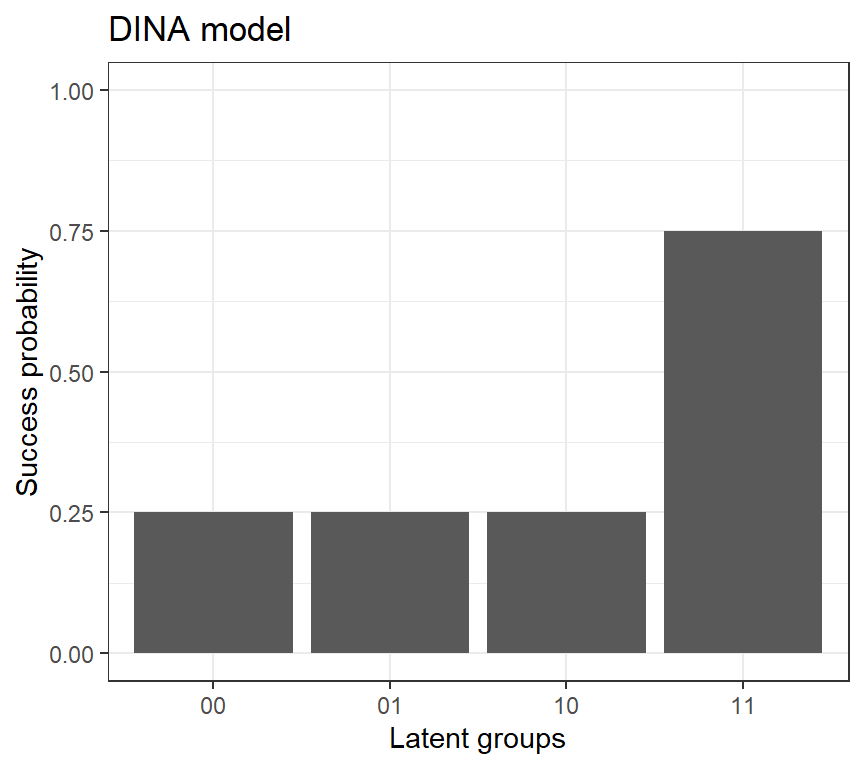
The IRF of the DINA model can be written by
\[ P(Y_{j}=1|\eta_{jl})= \begin{cases} g_j & \text{if $ η_{jl} = 0 $ }\\ 1-s_j & \text{if $ η_{jl} = 1 $} \end{cases} \]
The DINA model has only two parameters per item regardless of the number of attributes \(K\):
guessing parameter
slip parameter
Please find the parameters from the plot below: