3.9 The Generalized DINA model

The generalized DINA model, or G-DINA model, is a general model framework (de la Torre, 2011).

G-DINA model is often called a saturated model because it subsumes many existing CDMs ¹

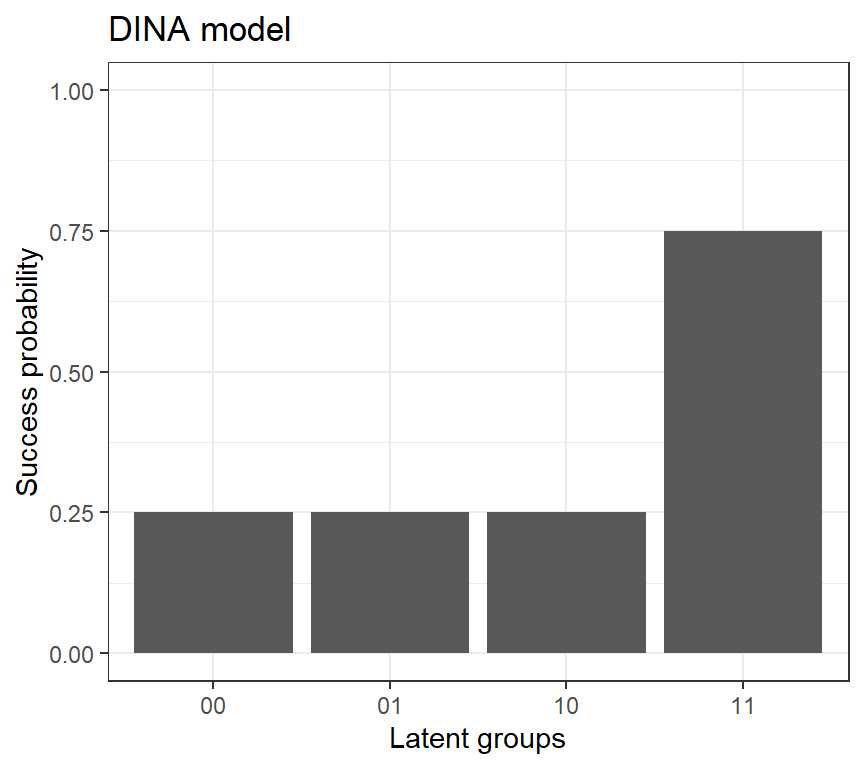
A revisit of the DINA model

A generalization

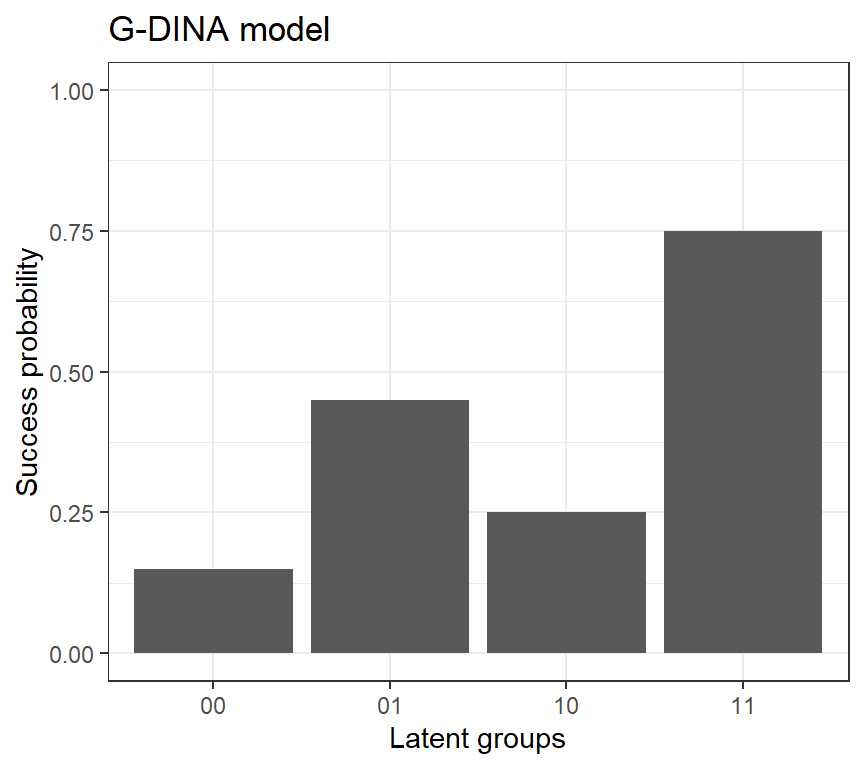
The IRF of the G-DINA model can be written by

$$P(Y_{j}=1|\alpha_{lj}^*)=\pi_{lj}$$

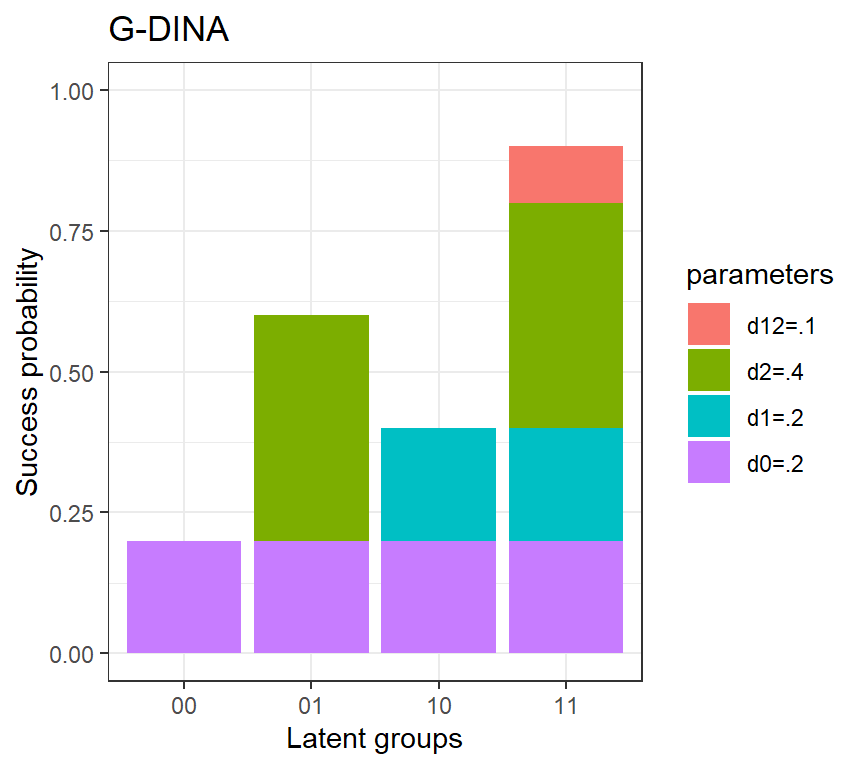
: Although the above IRF of the G-DINA model is very simple, researchers often reparmeterize it in a different, but equivalent, way:

$$P(Y_{j}=1|\alpha_{lj}^*)=\delta_{j0}+\sum_k^{K_j^*}\delta_{jk}\alpha_{lk}+\ldots+\delta_{j1,2,\ldots,K_j^*}\prod_k^{K_j^*}\alpha_{lk}$$

Based on this parameterization, which is often referred to as the identity link of the G-DINA model, please calculate the following probabilities of success:

$$\begin{aligned} P(Y_{j}=1|\alpha_{lj}^*=00) &= \delta_{j0} \\ P(Y_{j}=1|\alpha_{lj}^*=10) &= ? \\ P(Y_{j}=1|\alpha_{lj}^*=01) &= ? \\ P(Y_{j}=1|\alpha_{lj}^*=11) &= ? \\ \end{aligned}$$

References

Davier, M. (2008). A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology, 61(2), 287–307. https://doi.org/10.1348/000711007X193957

de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76(2), 179–199. https://doi.org/10.1007/s11336-011-9207-7

Henson, R. A., Templin, J. L., & Willse, J. T. (2009). Defining a Family of Cognitive Diagnosis Models Using Log-Linear Models with Latent Variables. Psychometrika, 74(2), 191–210. https://doi.org/10.1007/s11336-008-9089-5

---

1. Another two saturated CDMs are loglinear CDM (Henson et al., 2009) and the general diagnostic model (Davier, 2008)↩︎