3.7 Reduced RUM
The Reduced RUM is a reduction of the Reparameterized Unified Model (Hartz, n.d.)
The Reduced RUM allows each required attribute to contribute differentially to the probability of success
The probability of a correct response to item \(j\) for examinees who have mastered all the required attributes for the item is given by \(\pi_j^*\)
The penalty for not mastering attribute \(k\) is \(r_{jk}^*\)
An example
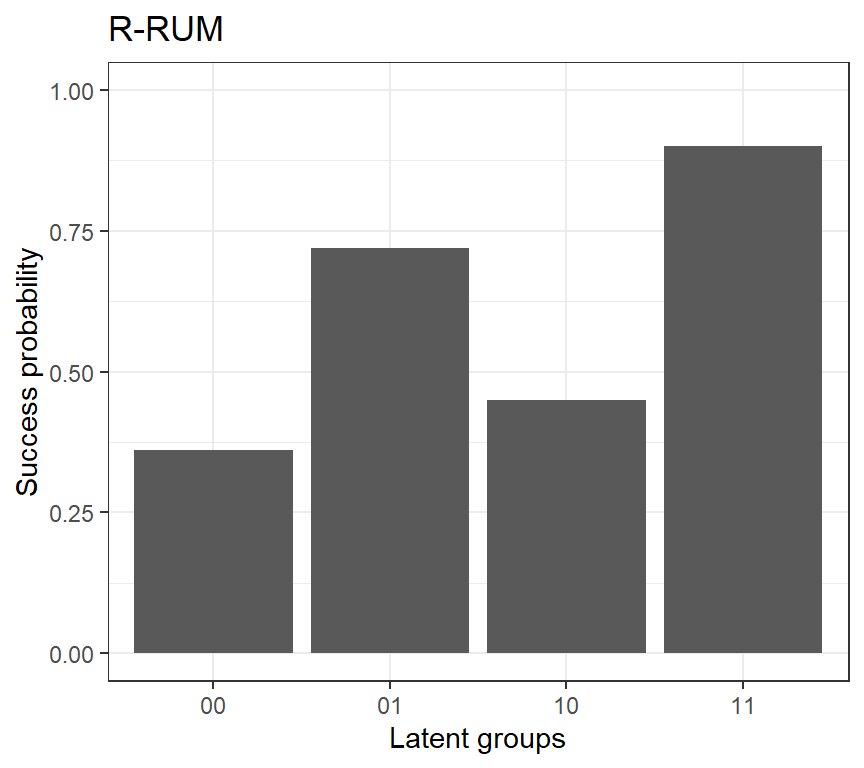
If an item measures attributes 1 and 2, there are four latent groups with reduced attribute profiles (00), (10), (01) and (11). Find the following success probabilities:
\[ P[Y_j=1|\alpha_{lj}^*=(0,0)]=?\\ P[Y_j=1|\alpha_{lj}^*=(1,0)]=?\\ P[Y_j=1|\alpha_{lj}^*=(0,1)]=?\\ P[Y_j=1|\alpha_{lj}^*=(1,1)]= \pi_j^* \]
The item response function of the Reduced RUM is
\[ P[Y_j=1|\alpha_{lj}^*]=\pi_j^*\prod_kr_{jk}^{*q_{jk}(1-\alpha_{jk})} \]
The plot below shows the RRUM with \(\pi_j^*=.9\),\(r_{j1}^*=.5\), and \(r_{j2}^*=.8\)