5.11 Bayesian approach for parameter estimation
In maximum likelihood estimation, we attempt to find parameters \(\{\mathbf{g},\mathbf{s}\}\) that can maximize the marginalized log likelihood \(\ell(\mathbf{Y})\).
In Bayesian framework, we aim to determine the posterior distribution of all model parameters \({\mathbf{g},\mathbf{s}},\ldots\): \[\begin{equation} P(\mathbf{g},\mathbf{s},\ldots|\mathbf{Y})=\frac{P(\mathbf{Y}|\mathbf{g},\mathbf{s},\ldots)p(\mathbf{g},\mathbf{s},\ldots)}{P(\mathbf{Y})} \end{equation}\]
Typically, in MCMC programs such as JAGS and nimble, one needs to specify two things:
- priors and
- model likelihood
All parameters have prior distributions
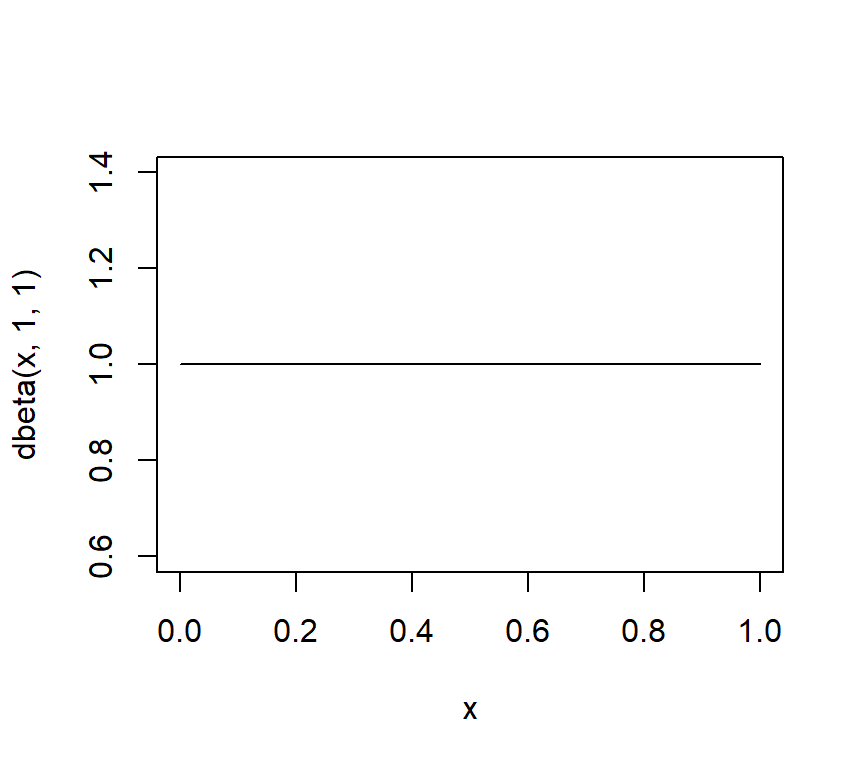
- Item parameters \(g\) and \(s\) follow \(beta(1,1)\), which is a uniform distribution ranging from 0 to 1:
Person’s latent class membership latent.group.index[n] follows a categorical distribution \(cat(p)\)
\(p\) in the categorical distribution \(cat(p)\) follows a dirichlet distribution \(dirich(\delta)\)
Regarding likelihood, we need to specify the likelihood of observing each item response:
\[\begin{equation} P(Y_{ij}=1|\mathbf{\alpha}_{c})= g_j + (1-s_j-g_j)I(\mathbf{\alpha}_{c}^T\mathbf{q}_j < \mathbf{q}_{j}^T\mathbf{q}_j) \end{equation}\]
Although MCMC is guaranteed to converge to the target distributions of model parameters, one may need a very long MCMC chain to achieve that.