3.14 The multivariate normal model for joint attribute distribution
The multivariate normal model is also referred to as unstructured tetrachoric model (Maris, 1999). This model assumes that attributes are generated from underlying continuous variables, which are usually assumed to be normally distributed.
Parameters in a multivariate normal model include \(K\) threshold parameters and \(\frac{K(K-1)}{2}\) tetrachoric correlation coefficients.
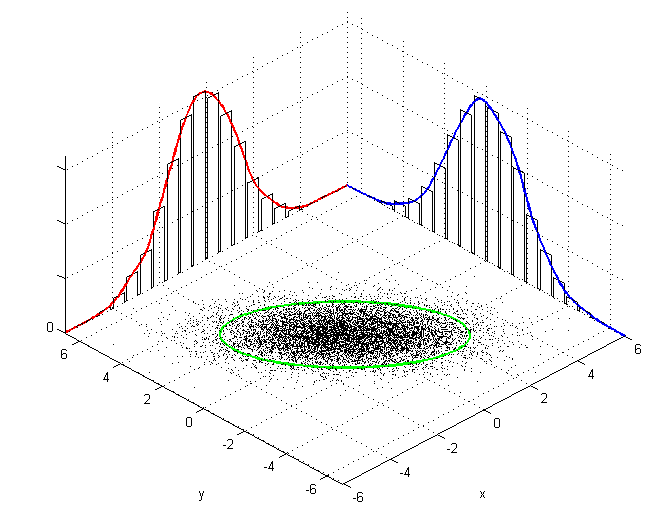
An example
What are the joint probabilities of two attributes in the following table under a multivariate normal model?
References
Maris, E. (1999). Estimating multiple classification latent class models. Psychometrika, 64(2), 187–212. https://doi.org/10.1007/bf02294535