1.11 転置
ベクトル・行列の転置とは行ベクトルと列ベクトルを入れ替えることをいう. ベクトルの転置については比較的簡単で
\[ \begin{align} \boldsymbol a &= \begin{pmatrix} a_1 & a_2 & \cdots & a_n \end{pmatrix} \\ \boldsymbol a^\top &= \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \end{align} \] という操作である.なお\(\top\)は転置する操作を表す.
次に行列の転置は行ベクトルを列ベクトルに,もしくは列ベクトルを行ベクトルとする操作である.イメージとしては左上から右下への直線を軸にくるっと回すような操作である.
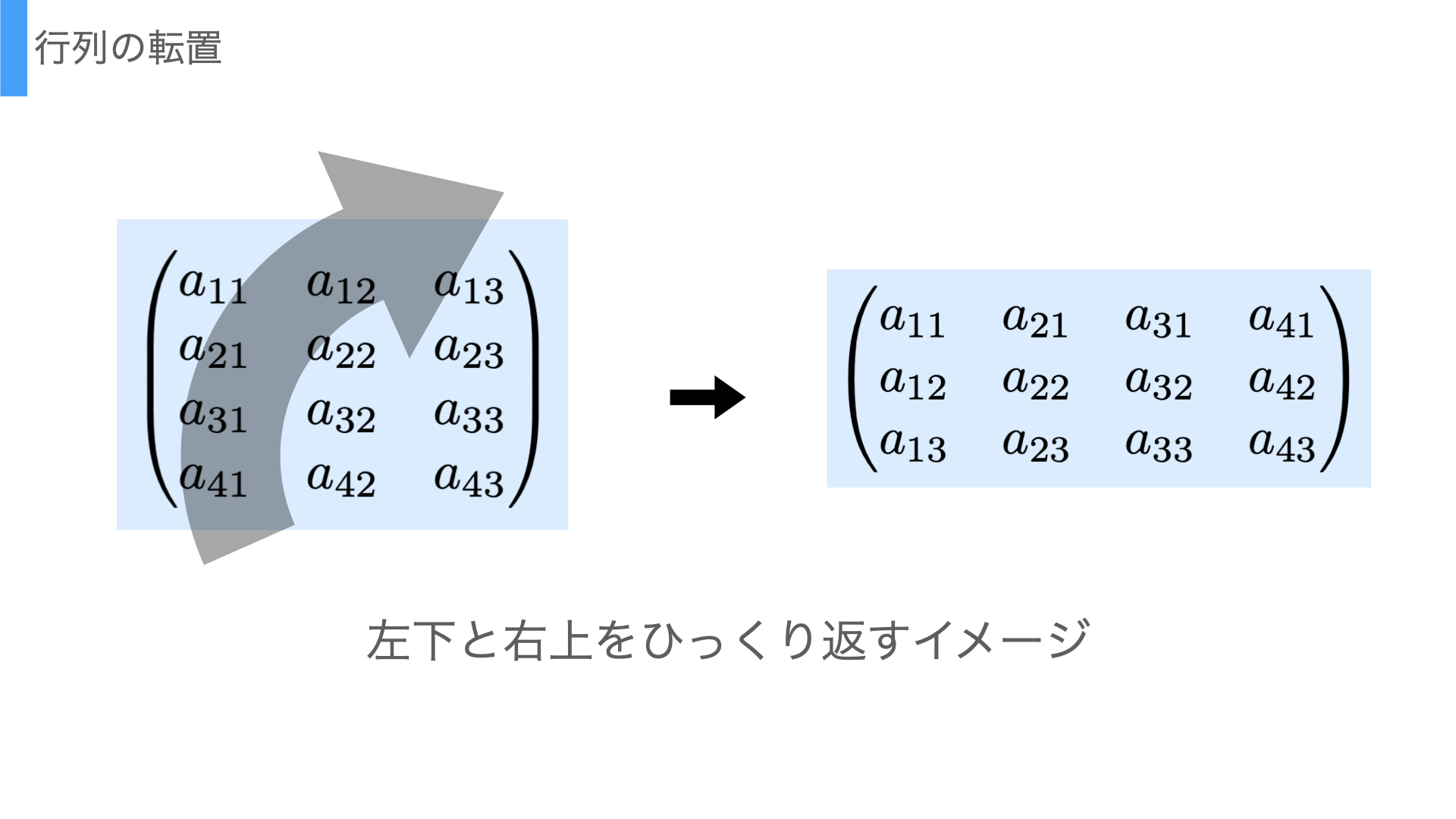
いま\(\boldsymbol a_{\cdot i} \in \mathbb R^{n}\)として
\[ A = \begin{pmatrix} \boldsymbol a_{\cdot 1} & \boldsymbol a_{\cdot 2} & \cdots & \boldsymbol a_{\cdot m} \end{pmatrix} \]
という\(n \times m\)行列を考えると,その転置\(A^\top\)は以下のように表せる.
\[ A^\top = \begin{pmatrix} \boldsymbol a^\top_{\cdot 1} \\ \boldsymbol a^\top_{\cdot 2} \\ \vdots \\ \boldsymbol a^\top_{\cdot m} \end{pmatrix} \]
Exercise 1.7 (ベクトルと行列の転置) 次のベクトル,行列についてそれぞれ転置したものを求めよ.
\[\begin{align} (1) \hspace{5mm} & \begin{pmatrix} 10 & 4 & 2 & 50 \end{pmatrix} \\ (2) \hspace{5mm} & \begin{pmatrix} 4 \\ 2 \\ 5 \end{pmatrix} \\ (3) \hspace{5mm} & \begin{pmatrix} 3 & 2 & 6 \\ 1 & 6 & 0 \\ 7 & 8 & 7 \end{pmatrix} \\ (4) \hspace{5mm} & \begin{pmatrix} 10 & 11 \\ 13 & 1 \\ 4 & 9 \end{pmatrix} \\ \end{align}\]