2.5 線型写像
あるベクトル\(\boldsymbol y\)が行列\(A\)とベクトル\(\boldsymbol x\)で表されるような状況を考える.
\[ \boldsymbol y = A \boldsymbol x \]
これは\(f(\boldsymbol x) = A \boldsymbol x\)のような\(\boldsymbol x\)の関数とも捉えられる.
関数を一般化した概念として写像というものがある.関数は写像の特別な場合である.
Definition 2.6 (写像) 集合\(X,Y\)とする.\({}^{\forall}\boldsymbol x \in X\)について\(Y\)のただ1つの元を対応させるものを写像という.ある写像\(f\)が\(X\)から\(Y\)への写像であることを
\(f : X \longrightarrow Y\)
と表す.このとき
- \(X\):\(f\)の定義域(始域)
- \(Y\):\(f\)の終域
- \(f(X)\):\(f\)の値域,象(Image)
などという.また,\(\text{Im}f\)を\(f\)の象を表す記号として用いることもある.
また,写像\(f\)によって\(x \in X\)と\(y \in Y\)に変換することを
\[\begin{align} f:x \longmapsto y \end{align}\]
と表す.
値域・終域とは写された元が属する集合であり,像とは写像によって写された元の集合であり終域全ての元が含まれるとは限らない.
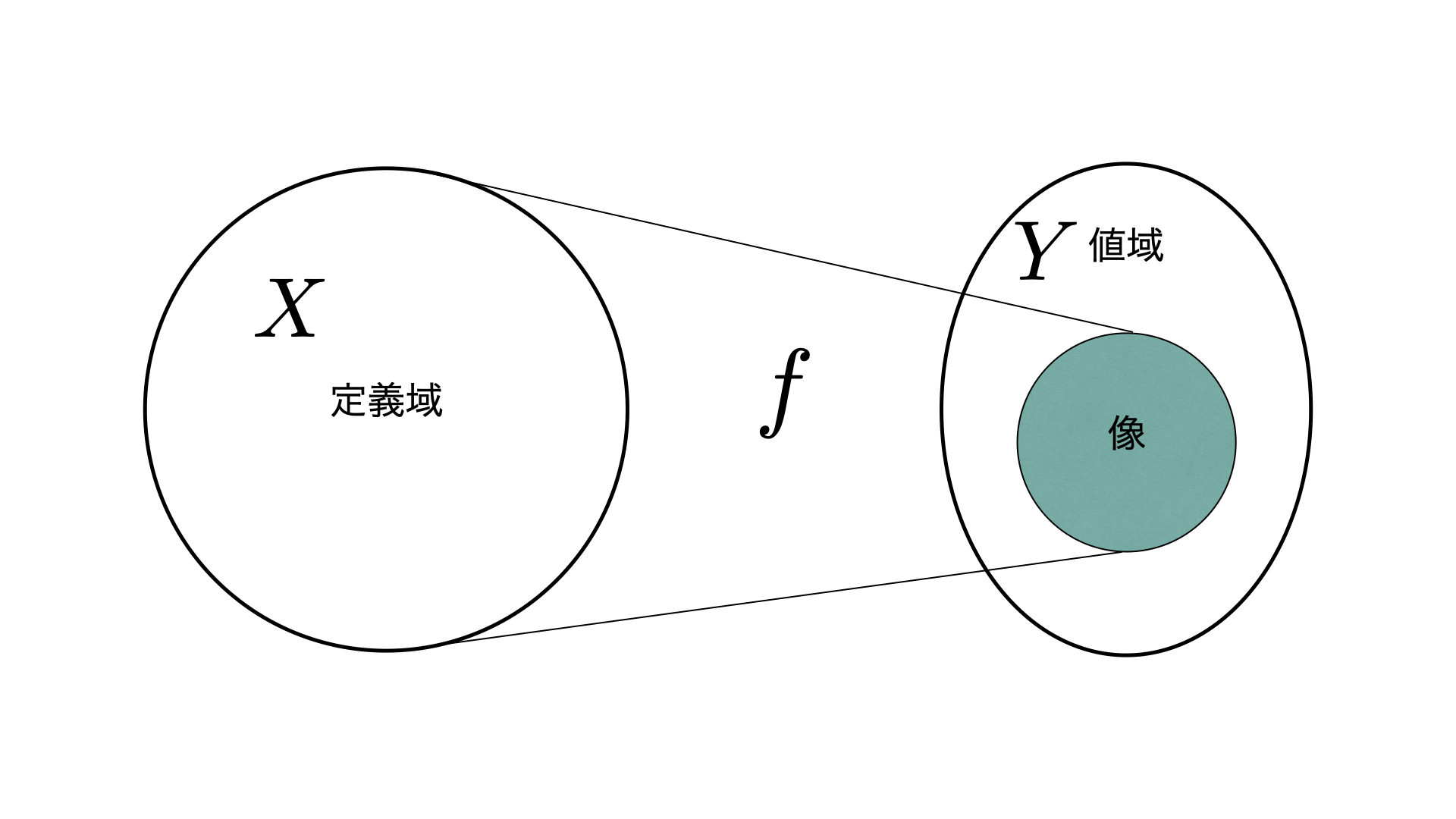
写像のが持つ性質によっていくつかの分類があり,それらの一部を紹介する.
Definition 2.7 (単射・全射) 写像\(f:X \longrightarrow Y\)について,\({}^{\forall}\boldsymbol x_1, \boldsymbol x_2, \boldsymbol x_1 \neq \boldsymbol x_2\)ならば\(f(\boldsymbol x_1) \neq f(\boldsymbol x_2)\)を満たす時,写像\(f\)は単射であるという.
また,\({}^{\forall}\boldsymbol y \in Y\)に対して\({}^{\exists}\boldsymbol x \in X\)であるとき,写像\(f\)は全射であるという.
写像\(f\)が単射かつ全射であるとき,全単射であるという.
単射とは,定義域の異なる元に対して写像によって写される先の元が同じであることは無いということを保証している. また,全射とは値域と像が一致することとも捉えられる.
Definition 2.8 (逆写像) 写像\(f:X \longrightarrow Y\)が全単射のとき,定義域\(X\)と値域\(Y\)の元は1対1対応の関係にある.すなわち,定義域を\(Y\)に,値域を\(X\)とした全単射となる写像\(g:Y \longrightarrow X\)を構成することができる. また,\({}^{\forall}\boldsymbol y \in Y\)に対して,\(\boldsymbol y = f(\boldsymbol x)\)となるような\(\boldsymbol x\)に写す写像を\(f^{-1}\)と表し\(f^{-1}:Y \longrightarrow X, \boldsymbol x = f^{-1}(\boldsymbol y)\)で定義される写像を写像\(f\)の逆写像という.
Definition 2.9 (線形写像) ベクトル空間\(V,W\)について,写像\(f:V \longrightarrow W\)が次の2つの条件を満たす時,\(f\)を\(V\)から\(W\)への線形写像であるという.
- \({}^{\forall}\boldsymbol v_1, \boldsymbol v_2 \in V \Rightarrow f(\boldsymbol v_1 + \boldsymbol v_2) = f(\boldsymbol v_1) + f(\boldsymbol v_2)\)
- \({}^{\forall}\boldsymbol v \in V, {}^{\forall}c \in \mathbb R\Rightarrow f(c \boldsymbol v) = c f(\boldsymbol v)\)
特に\(f:V \longrightarrow V\)の時,\(f\)を線形変換という.
\(\boldsymbol x A = \boldsymbol y\)という変換はまさに線形写像である.
Theorem 2.7 (行列と線型写像) ベクトル空間\(\mathbb R^{n}, \mathbb R^{m}\),行列\(A \in \mathbb R^{m\times n}\),ベクトル\(\boldsymbol x \in \mathbb R^{n}, \boldsymbol y \in \mathbb R^{m}\)を考える. このとき,写像\(f_A:\mathbb R^{n} \longrightarrow \mathbb R^{m}\)を
\[\begin{align} \boldsymbol y = f_A(\boldsymbol x) = A \boldsymbol x \end{align}\]
とすると,\(f_A\)は線形写像となる.
逆に,任意の線形写像\(g:\mathbb R^{m} \longrightarrow \mathbb R^{n}\)を考えた時,
\[\begin{align} \boldsymbol y = g(\boldsymbol x) = A \boldsymbol x \end{align}\]
となるような行列\(A \in \mathbb R^{m\times n}\)が一意に存在する.
Theorem 2.8 (線形写像の性質) ベクトル空間\(\mathbb R^{n}, \mathbb R^{m}, \mathbb R^{k}\)について,二つの線形写像\(f:\mathbb R^{n} \longrightarrow \mathbb R^{m}\)と\(g:\mathbb R^{m} \longrightarrow \mathbb R^{k}\)を考える.このとき,写像\(f\)によって\(\mathbb R^{n}\)から\(\mathbb R^{m}\)に写された元をさらに\(\mathbb R^{k}\)に写すような写像を\(f\)と\(g\)の合成写像といい\(g \circ f\)と表す.この写像は\(\mathbb R^{n} \longrightarrow \mathbb R^{k}\)への写像と見なすことができる.
Definition 2.10 (カーネル) 写像\(f:X \longrightarrow Y\)について
\[\begin{align} K(f) := \{ \boldsymbol x \in X | f(\boldsymbol x) = \boldsymbol 0 \} \end{align}\]
となる集合を写像\(f\)のカーネルと呼ぶ.
カーネルとは,像におけるゼロベクトルに対応する定義域の元の集合である.
Exercise 2.4 (写像の種類とカーネル) 次の行列\(A\)は\(\mathbb R^2 \rightarrow \mathbb R^2\)への写像\(f\)をなす。\(f\)のカーネルを求めよ。
\[\begin{align} A = \begin{pmatrix} 4 & 2 \\ 2 & 1 \end{align}\]