6.3 Kernel regression with mixed multivariate data

Until now, we have studied the simplest situation for performing nonparametric estimation of the regression function: a single, continuous, predictor \(X\) is available for explaining \(Y,\) a continuous response. This served for introducing the main concepts without the additional technicalities associated to more complex predictors. We now extend the study to the case in which there are

• multiple predictors \(X_1,\ldots,X_p\) and
• possible non-continuous predictors, namely categorical predictors and discrete predictors.

The first point is how to extend the local polynomial estimator \(\hat{m}(\cdot;q,h)\;\)²²⁷ to deal with \(p\) continuous predictors. Although this can be done for \(q\geq0,\) we focus on the local constant and linear estimators (\(q=0,1\)) for avoiding excessive technical complications.²²⁸ Also, to avoid a quickly escalation of the number of smoothing bandwidths, it is customary to consider product kernels. With these two restrictions, the estimators for \(m\) based on a sample \(\{(\mathbf{X}_i,Y_i)\}_{i=1}^n\) extend easily from the developments in Sections 6.2.1 and 6.2.2:

• Local constant estimator. We can replicate the argument in (6.13) with a multivariate kde for \(f_{\mathbf{X}}\) based on product kernels with bandwidth vector \(\mathbf{h},\) which gives

  \[\begin{align*} \hat{m}(\mathbf{x};0,\mathbf{h}):=\sum_{i=1}^n\frac{K_\mathbf{h}(\mathbf{x}-\mathbf{X}_i)}{\sum_{i=1}^nK_\mathbf{h}(\mathbf{x}-\mathbf{X}_i)}Y_i=\sum_{i=1}^nW^0_{i}(\mathbf{x})Y_i \end{align*}\]

  where

  \[\begin{align*} K_\mathbf{h}(\mathbf{x}-\mathbf{X}_i)&:=K_{h_1}(x_1-X_{i1})\times\stackrel{p}{\cdots}\times K_{h_p}(x_p-X_{ip}),\\ W^0_{i}(\mathbf{x})&:=\frac{K_\mathbf{h}(\mathbf{x}-\mathbf{X}_i)}{\sum_{i=1}^nK_\mathbf{h}(\mathbf{x}-\mathbf{X}_i)}. \end{align*}\]

• Local linear estimator. Considering the Taylor expansion \(m(\mathbf{X}_i)\approx m(\mathbf{x})+\nabla m(\mathbf{x})(\mathbf{X}_i-\mathbf{x})\;\)²²⁹ instead of (6.18) it is possible to arrive to the analogous of (6.21),

  \[\begin{align*} \hat{\boldsymbol{\beta}}_\mathbf{h}:=\arg\min_{\boldsymbol{\beta}\in\mathbb{R}^{p+1}}\sum_{i=1}^n\left(Y_i-\boldsymbol{\beta}'(1,(\mathbf{X}_i-\mathbf{x})')'\right)^2K_\mathbf{h}(\mathbf{x}-\mathbf{X}_i), \end{align*}\]

  and then solve the problem in the exact same way but now considering

  \[\begin{align*} \mathbf{X}:=\begin{pmatrix} 1 & (\mathbf{X}_1-\mathbf{x})'\\ \vdots & \vdots\\ 1 & (\mathbf{X}_n-\mathbf{x})'\\ \end{pmatrix}_{n\times(p+1)} \end{align*}\]

  and

  \[\begin{align*} \mathbf{W}:=\mathrm{diag}(K_{\mathbf{h}}(\mathbf{X}_1-\mathbf{x}),\ldots, K_\mathbf{h}(\mathbf{X}_n-\mathbf{x})). \end{align*}\]

  The estimate²³⁰ for \(m(x)\) is therefore computed as

  \[\begin{align*} \hat{m}(\mathbf{x};1,h):=&\,\hat{\beta}_{\mathbf{h},0}\\ =&\,\mathbf{e}_1'(\mathbf{X}'\mathbf{W}\mathbf{X})^{-1}\mathbf{X}'\mathbf{W}\mathbf{Y}\\ =&\,\sum_{i=1}^nW^1_{i}(\mathbf{x})Y_i \end{align*}\]

  where

  \[\begin{align*} W^1_{i}(\mathbf{x}):=\mathbf{e}_1'(\mathbf{X}'\mathbf{W}\mathbf{X})^{-1}\mathbf{X}'\mathbf{W}\mathbf{e}_i. \end{align*}\]

The cross-validation bandwidth selection rule studied on Section 6.2.4 extends neatly to the multivariate case:

\[\begin{align*} \mathrm{CV}(\mathbf{h})&:=\frac{1}{n}\sum_{i=1}^n(Y_i-\hat{m}_{-i}(\mathbf{X}_i;p,\mathbf{h}))^2,\\ \hat{\mathbf{h}}_\mathrm{CV}&:=\arg\min_{h_1,\ldots,h_p>0}\mathrm{CV}(\mathbf{h}). \end{align*}\]

Obvious complications appear in the optimization of \(\mathrm{CV}(\mathbf{h}),\) which now is a \(\mathbb{R}^p\rightarrow\mathbb{R}\) function. Importantly, the trick described in Proposition 6.1 also holds with obvious modifications.

Let’s see an application of multivariate kernel regression for the wine dataset.

# Employing the wine dataset
wine <- read.table(file = "wine.csv", header = TRUE, sep = ",")

# Bandwidth by CV for local linear estimator -- a product kernel with 4
# bandwidths. Employs 4 random starts for minimizing the CV surface
bwWine <- np::npregbw(formula = Price ~ Age + WinterRain + AGST + HarvestRain,
                      data = wine, regtype = "ll")
bwWine
## 
## Regression Data (27 observations, 4 variable(s)):
## 
##                   Age WinterRain      AGST HarvestRain
## Bandwidth(s): 3616691  290170218 0.8725243    106.5079
## 
## Regression Type: Local-Linear
## Bandwidth Selection Method: Least Squares Cross-Validation
## Formula: Price ~ Age + WinterRain + AGST + HarvestRain
## Bandwidth Type: Fixed
## Objective Function Value: 0.0873955 (achieved on multistart 4)
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 4

# Regression
fitWine <- np::npreg(bwWine)
summary(fitWine)
## 
## Regression Data: 27 training points, in 4 variable(s)
##                   Age WinterRain      AGST HarvestRain
## Bandwidth(s): 3616691  290170218 0.8725243    106.5079
## 
## Kernel Regression Estimator: Local-Linear
## Bandwidth Type: Fixed
## Residual standard error: 0.2079691
## R-squared: 0.8889649
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 4

# Plot marginal effects of each predictor on the response (the rest of
# predictors are fixed to their marginal medians)
plot(fitWine)
# Therefore:
# - Age is positively related with Price (almost linearly)
# - WinterRain is positively related with Price (with a subtle nonlinearity)
# - AGST is positively related with Price, but now we see what it looks like a
#   quadratic pattern
# - HarvestRain is negatively related with Price (almost linearly)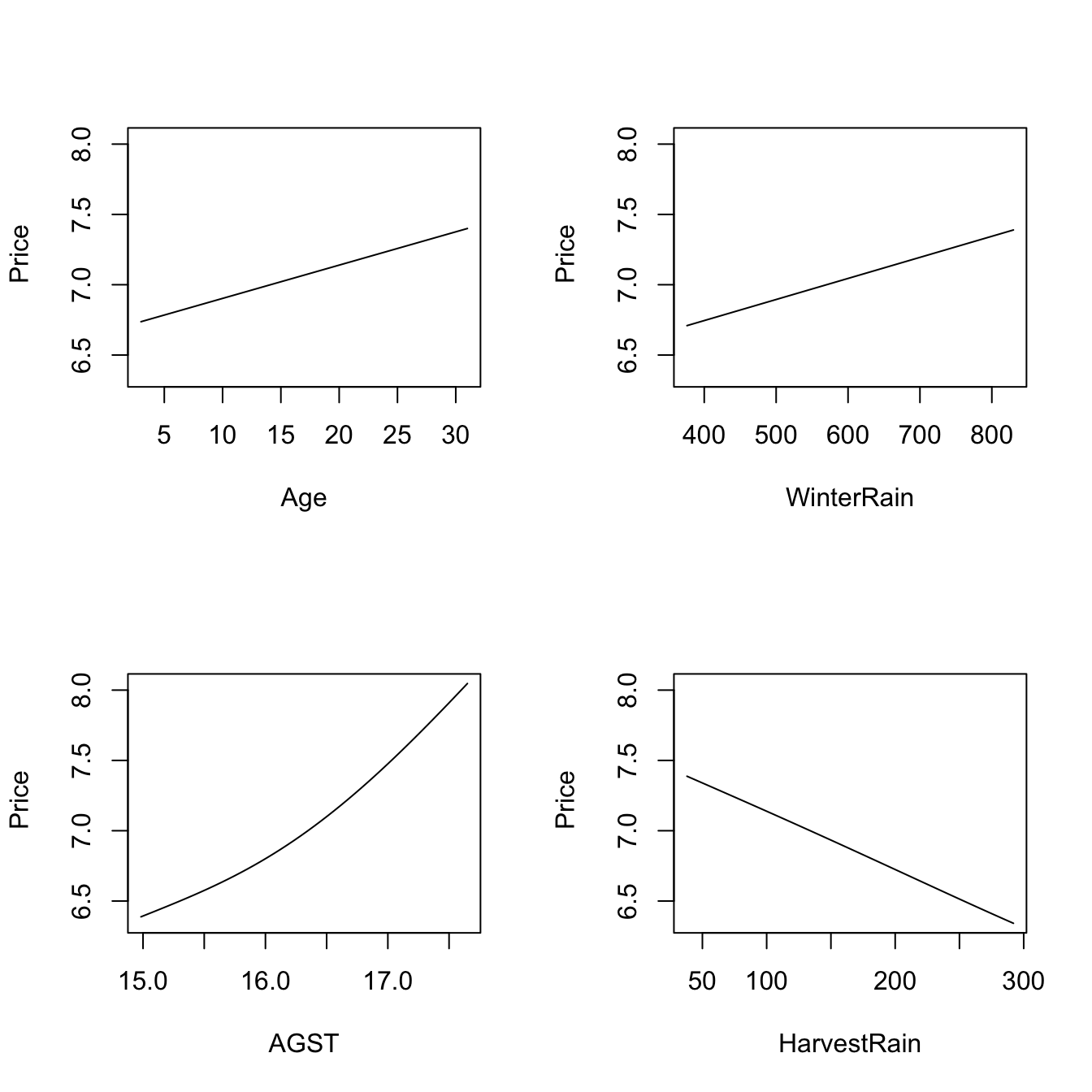

The \(R^2\) outputted by the summary of np::npreg is defined as

\[\begin{align*} R^2:=\frac{(\sum_{i=1}^n(Y_i-\bar{Y})(\hat{Y}_i-\bar{Y}))^2}{(\sum_{i=1}^n(Y_i-\bar{Y})^2)(\sum_{i=1}^n(\hat{Y}_i-\bar{Y})^2)} \end{align*}\]

and is neither the \(r^2_{y\hat{y}}\) (because it is not guaranteed that \(\bar{Y}=\bar{\hat{Y}}\)!) nor “the percentage of variance explained” by the model – this interpretation only makes sense within the linear model context. It is however a quantity in \([0,1]\) that attains \(R^2=1\) when the fit is perfect.

Non-continuous variables can be taken into account by defining suitably adapted kernels. The two main possibilities for non-continuous data are:

• Categorical or unordered discrete variables. For example, iris$species is a categorical variable in which ordering does not make sense. These variables are specified in R by factor. Due to the lack of ordering, the basic mathematical operation behind a kernel, a distance computation,²³¹ is senseless. That motivates the Aitchison and Aitken (1976) kernel.

  Assume that the categorical random variable \(X_d\) has \(c_d\) different levels. Then, it can be represented as \(X_d\in C_d:=\{0,1,\ldots,c_d-1\}.\) For \(x_d,X_d\in C_d,\) the Aitchison and Aitken (1976) unordered discrete kernel is

  \[\begin{align*} l(x_d,X_d;\lambda)=\begin{cases} 1-\lambda,&\text{ if }x_d=X_d,\\ \frac{\lambda}{c_d-1},&\text{ if }x_d\neq X_d, \end{cases} \end{align*}\]

  where \(\lambda\in[0,(c_d-1)/c_d]\) is the bandwidth.

• Ordinal or ordered discrete variables. For example, wine$Year is a discrete variable with a clear order, but it is not continuous. These variables are specified by ordered (an ordered factor). In these variables there is ordering, but distances are discrete.

  If the ordered discrete random variable \(X_d\) can take \(c_d\) different ordered values, then it can be represented as \(X_d\in C_d:=\{0,1,\ldots,c_d-1\}.\) For \(x_d,X_d\in C_d,\) a possible (Li and Racine 2007) ordered discrete kernel is

  \[\begin{align*} l(x_d,X_d;\lambda)=\lambda^{|x_d-X_d|}, \end{align*}\]

  where \(\lambda\in[0,1]\) is the bandwidth.

The np package employs a variation of the previous kernels. The following examples illustrate their use.

# Bandwidth by CV for local linear estimator
# Recall that Species is a factor!
bwIris <- np::npregbw(formula = Petal.Length ~ Sepal.Width + Species,
                      data = iris, regtype = "ll")
bwIris
## 
## Regression Data (150 observations, 2 variable(s)):
## 
##               Sepal.Width      Species
## Bandwidth(s):    898696.6 2.357536e-07
## 
## Regression Type: Local-Linear
## Bandwidth Selection Method: Least Squares Cross-Validation
## Formula: Petal.Length ~ Sepal.Width + Species
## Bandwidth Type: Fixed
## Objective Function Value: 0.1541057 (achieved on multistart 1)
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 1
## 
## Unordered Categorical Kernel Type: Aitchison and Aitken
## No. Unordered Categorical Explanatory Vars.: 1
# Product kernel with 2 bandwidths

# Regression
fitIris <- np::npreg(bwIris)
summary(fitIris)
## 
## Regression Data: 150 training points, in 2 variable(s)
##               Sepal.Width      Species
## Bandwidth(s):    898696.6 2.357536e-07
## 
## Kernel Regression Estimator: Local-Linear
## Bandwidth Type: Fixed
## Residual standard error: 0.3775005
## R-squared: 0.9539633
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 1
## 
## Unordered Categorical Kernel Type: Aitchison and Aitken
## No. Unordered Categorical Explanatory Vars.: 1

# Plot marginal effects of each predictor on the response
par(mfrow = c(1, 2))
plot(fitIris, plot.par.mfrow = FALSE)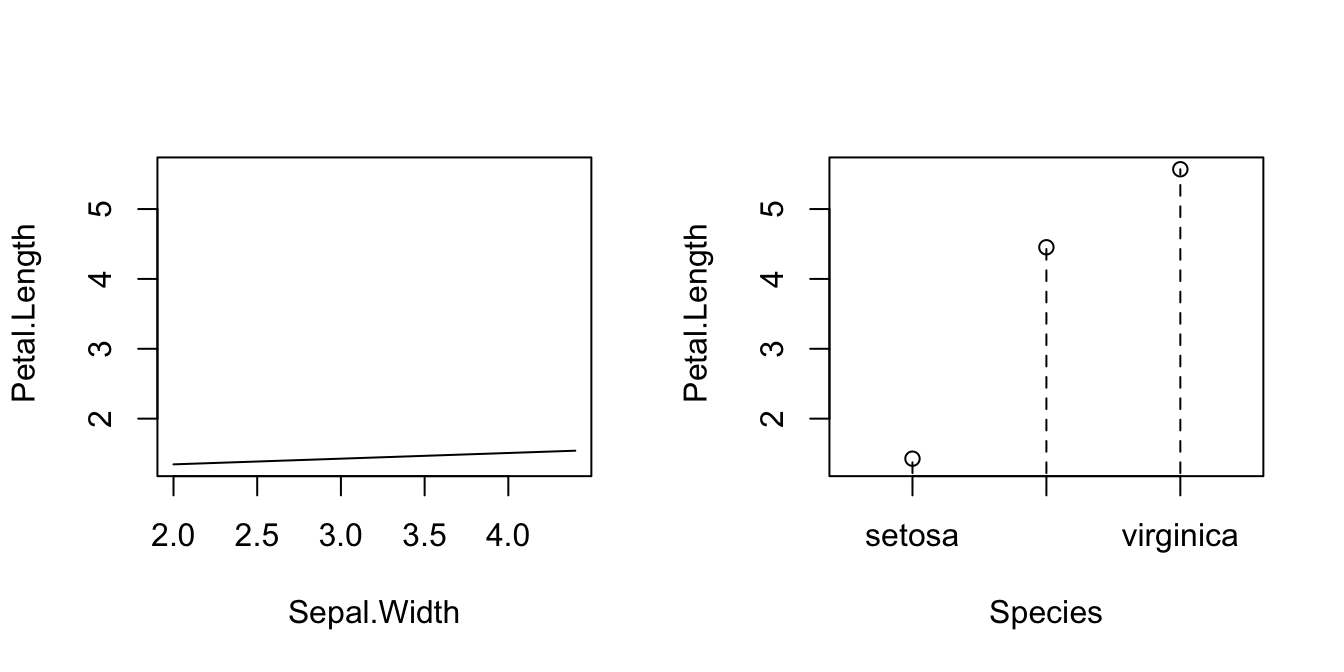

# Options for the plot method for np::npreg available at ?np::npplot
# For example, xq = 0.5 (default) indicates that all the predictors are set to
# their medians for computing the marginal effects

# Example from ?np::npreg: modeling of the GDP growth of a country from
# economic indicators of the country
# The predictors contain a mix of unordered, ordered, and continuous variables

# Load data
data(oecdpanel, package = "np")

# Bandwidth by CV for local constant -- use only two starts to reduce the
# computation time
bwOECD <- np::npregbw(formula = growth ~ factor(oecd) + ordered(year) +
                        initgdp + popgro + inv + humancap, data = oecdpanel,
                      regtype = "lc", nmulti = 2)
bwOECD
## 
## Regression Data (616 observations, 6 variable(s)):
## 
##               factor(oecd) ordered(year)   initgdp  popgro        inv humancap
## Bandwidth(s):   0.02413475     0.8944088 0.1940763 9672508 0.09140376 1.223202
## 
## Regression Type: Local-Constant
## Bandwidth Selection Method: Least Squares Cross-Validation
## Formula: growth ~ factor(oecd) + ordered(year) + initgdp + popgro + inv + 
##     humancap
## Bandwidth Type: Fixed
## Objective Function Value: 0.0006545946 (achieved on multistart 2)
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 4
## 
## Unordered Categorical Kernel Type: Aitchison and Aitken
## No. Unordered Categorical Explanatory Vars.: 1
## 
## Ordered Categorical Kernel Type: Li and Racine
## No. Ordered Categorical Explanatory Vars.: 1

# Regression
fitOECD <- np::npreg(bwOECD)
summary(fitOECD)
## 
## Regression Data: 616 training points, in 6 variable(s)
##               factor(oecd) ordered(year)   initgdp  popgro        inv humancap
## Bandwidth(s):   0.02413475     0.8944088 0.1940763 9672508 0.09140376 1.223202
## 
## Kernel Regression Estimator: Local-Constant
## Bandwidth Type: Fixed
## Residual standard error: 0.01814086
## R-squared: 0.6768302
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 4
## 
## Unordered Categorical Kernel Type: Aitchison and Aitken
## No. Unordered Categorical Explanatory Vars.: 1
## 
## Ordered Categorical Kernel Type: Li and Racine
## No. Ordered Categorical Explanatory Vars.: 1

# Plot marginal effects of each predictor
par(mfrow = c(2, 3))
plot(fitOECD, plot.par.mfrow = FALSE)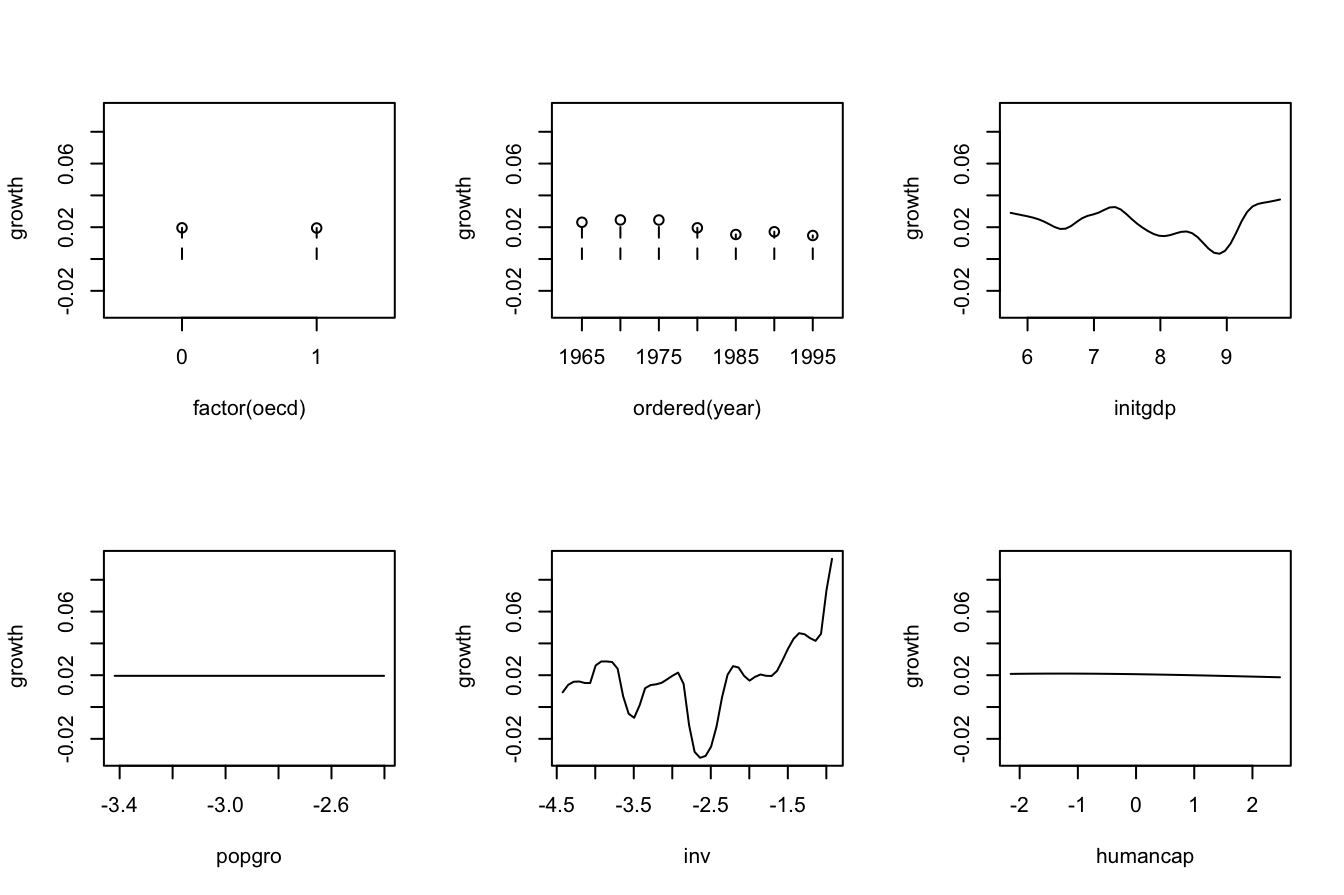

References

Aitchison, J., and C. G. G. Aitken. 1976. “Multivariate Binary Discrimination by the Kernel Method.” Biometrika 63 (3): 413–20. https://doi.org/10.1093/biomet/63.3.413.

Li, Q., and J. S. Racine. 2007. Nonparametric Econometrics. Princeton: Princeton University Press. https://press.princeton.edu/books/hardcover/9780691121611/nonparametric-econometrics.

---

227. Now \(q\) denotes the order of the polynomial fit since \(p\) stands for the number of predictors.↩︎

228. In particular, the consideration of Taylor expansions of \(m:\mathbb{R}^p\rightarrow\mathbb{R}\) of more than two orders that involve the consideration of the vector of partial derivatives \(\mathrm{D}^{\otimes s}m(\mathbf{x})\) formed by \(\frac{\partial^s m(\mathbf{x})}{\partial x_1^{s_1}\cdots \partial x_p^{s_1}},\) where \(s=s_1+\cdots+s_p.\) For example: if \(s=1,\) then \(\mathrm{D}^{\otimes 1}m(\mathbf{x})\) is just the transpose of the gradient \(\nabla m(\mathbf{x})';\) if \(s=2,\) then \(\mathrm{D}^{\otimes 2}m(\mathbf{x})\) is the column stacking of the Hessian matrix \(\mathcal{H}m(\mathbf{x});\) and if \(s\geq3\) the arrangement of derivatives is made in terms of tensors containing the derivatives \(\frac{\partial^s m(\mathbf{x})}{\partial x_1^{s_1}\cdots \partial x_p^{s_1}}.\)↩︎

229. The gradient \(\nabla m(\mathbf{x})=\left(\frac{\partial m(\mathbf{x})}{\partial x_1},\ldots,\frac{\partial m(\mathbf{x})}{\partial x_p}\right)\) is a row vector.↩︎

230. Recall that now the entries of \(\hat{\boldsymbol{\beta}}_\mathbf{h}\) are estimating \(\boldsymbol{\beta}=\left(m(\mathbf{x}), \nabla m(\mathbf{x})\right)'.\)↩︎

231. Recall \(K_h(x-X_i).\)↩︎