6.4 Prediction and confidence intervals
The prediction of the conditional response \(m(\mathbf{x})=\mathbb{E}[Y|\mathbf{X}=\mathbf{x}]\) with the local polynomial estimator reduces to evaluate \(\hat{m}(\mathbf{x};p,\mathbf{h}).\) The fitted values are, therefore, \(\hat{Y}_i:=\hat{m}(\mathbf{X}_i;p,\mathbf{h}),\) \(i=1,\ldots,n.\) The np package has methods to perform these operations via the predict and fitted functions.
More interesting is the discussion about the uncertainty of \(\hat{m}(\mathbf{x};p,\mathbf{h})\) and, as a consequence, of the predictions. Differently to what happened in parametric models, in nonparametric regression there is no parametric distribution of the response that can help to carry out the inference and, consequently, to address the uncertainty of the estimation. Because of this, it is required to resort to somehow convoluted asymptotic expressions233 (carried out by predict if se.fit = TRUE) or to bootstrap resampling procedures. The default bootstrap resampling procedure in np is the so-called wild bootstrap (Liu 1988), which is particularly well-suited for regression problems with potential heteroscedasticity.
Due to their increasing complexity, we just cover very superficially these methods with the following example.
# Asymptotic confidence bands for the marginal effects of each predictor on the
# response
par(mfrow = c(2, 3))
plot(fitOECD, plot.errors.method = "asymptotic", common.scale = FALSE,
plot.par.mfrow = FALSE)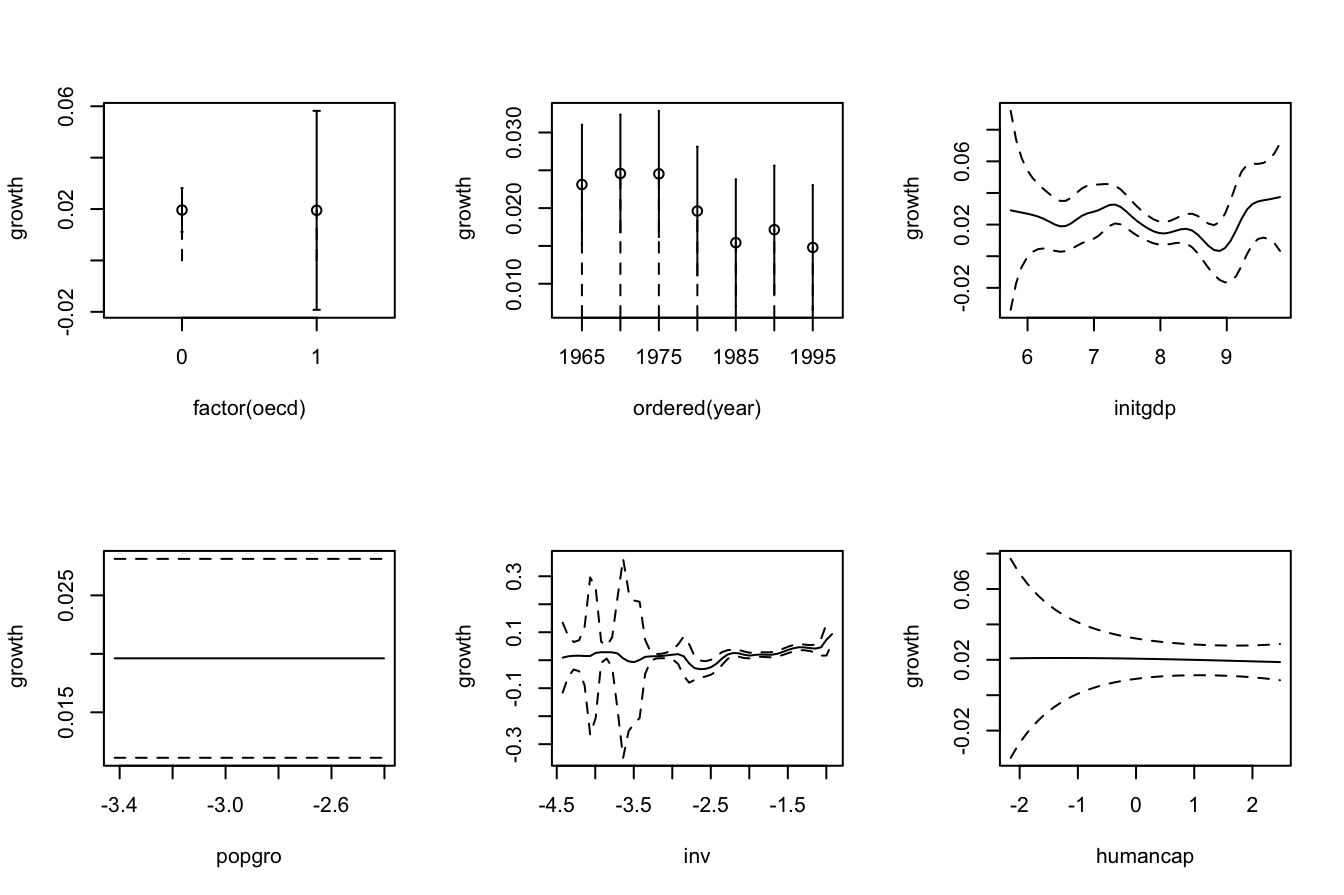
# Bootstrap confidence bands
# They take more time to compute because a resampling + refitting takes place
par(mfrow = c(2, 3))
plot(fitOECD, plot.errors.method = "bootstrap", plot.par.mfrow = FALSE)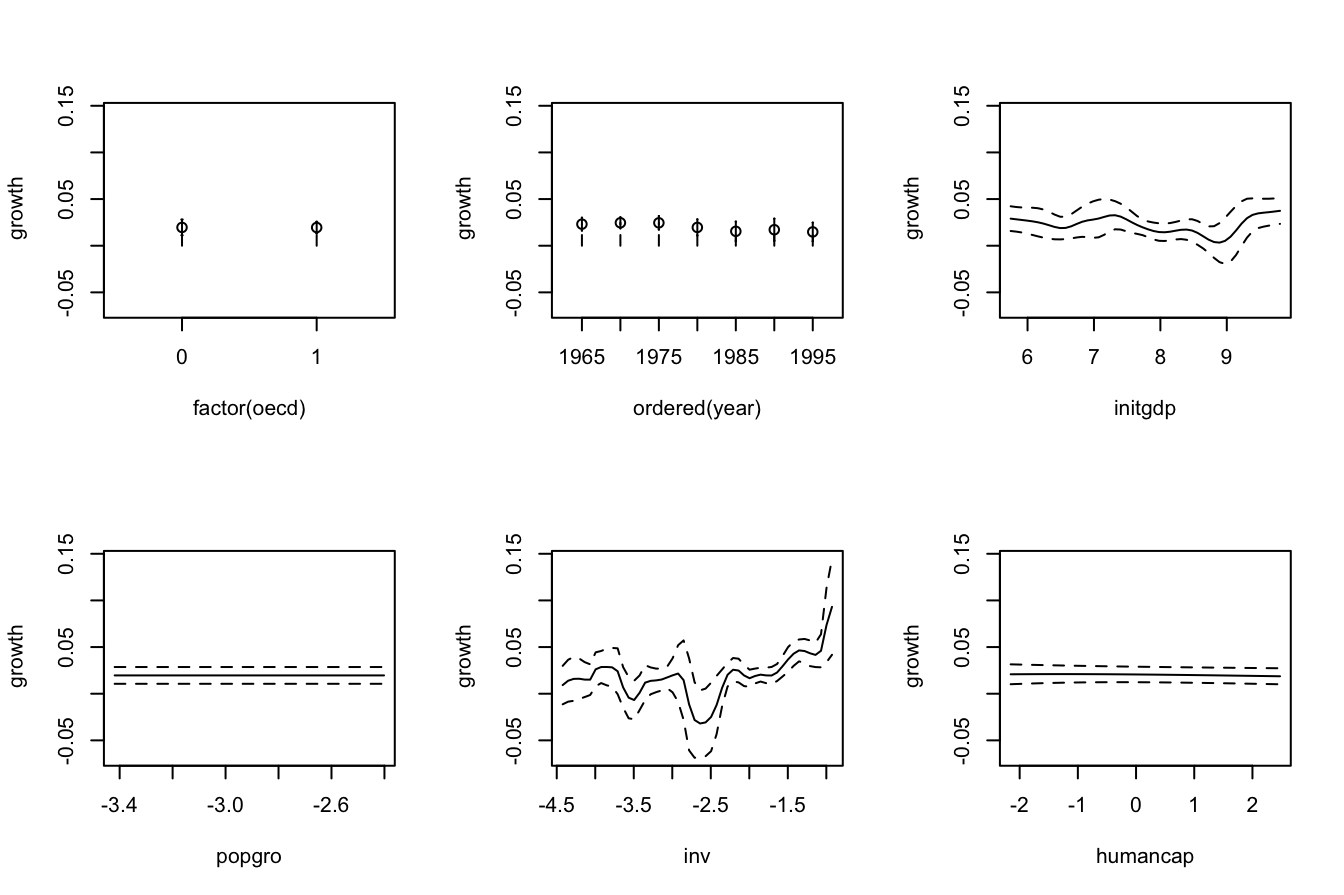
# The asymptotic standard error associated to the regression evaluated at the
# evaluation points are in $merr
head(fitOECD$merr)
## [1] 0.004534787 0.006105144 0.001558307 0.002400982 0.006213965 0.005274139
# Recall that in $mean we had the regression evaluated at the evaluation points,
# by default the sample of the predictors, so in this case the same as the
# fitted values
head(fitOECD$mean)
## [1] 0.02877743 0.02113513 0.03592755 0.04027579 0.01099637 0.03888485
# Prediction for the first 3 points + standard errors
pred <- predict(fitOECD, newdata = oecdpanel[1:3, ], se.fit = TRUE)
# Approximate (based on assuming asymptotic normality) 100(1 - alpha)% CI for
# the conditional mean of the first 3 points
alpha <- 0.05
pred$fit + (qnorm(1 - alpha / 2) * pred$se.fit) %o% c(-1, 1)
## [,1] [,2]
## [1,] 0.019889408 0.03766545
## [2,] 0.009169271 0.03310100
## [3,] 0.032873327 0.03898178Extrapolation with kernel regression estimators is particularly dangerous. Keep in mind that the kernel estimators smooth the data in order to estimate \(m,\) the trend. If there is no data close to the point \(\mathbf{x}\) at which \(m(\mathbf{x})\) is estimated, then the estimation will heavily depend on the closest data point to \(\mathbf{x}.\) If employing compactly-supported kernels (so that they can take the value \(0\) exactly), the estimate may not be even properly defined.