1.2 What is Predictive Modeling?
Predictive modeling is the process of developing a mathematical tool or model that generates an accurate prediction about a random quantity of interest.
In predictive modeling we are interested in predicting a random variable, typically denoted by \(Y,\) from a set of related variables \(X_1,\ldots,X_p.\) The focus is on learning what is the probabilistic model that relates \(Y\) with \(X_1,\ldots,X_p,\) and use that acquired knowledge for predicting \(Y\) given an observation of \(X_1,\ldots,X_p.\) Some concrete examples of this are:
- Predicting the wine quality (\(Y\)) from a set of environmental variables (\(X_1,\ldots,X_p\)).
- Predicting the number of sales (\(Y\)) from a set of marketing investments (\(X_1,\ldots,X_p\)).
- Modeling the average house value in a given suburb (\(Y\)) from a set of community-related features (\(X_1,\ldots,X_p\)).
- Predicting the probability of failure (\(Y\)) of a rocket launcher from the ambient temperature (\(X_1\)).
- Predicting students academic performance (\(Y\)) according to education resources and learning methodologies (\(X_1,\ldots,X_p\)).
- Predicting the fuel consumption of a car (\(Y\)) from a set of driving variables (\(X_1,\ldots,X_p\)).
The process of predictive modeling can be statistically abstracted in the following way. We believe that \(Y\) and \(X_1,\ldots,X_p\) are related by a regression model of the form
\[\begin{align} Y=m(X_1,\ldots,X_p)+\varepsilon,\tag{1.1} \end{align}\]
where \(m\) is the regression function and \(\varepsilon\) is a random error with zero mean that accounts for the uncertainty of knowing \(Y\) if \(X_1,\ldots,X_p\) are known. The function \(m:\mathbb{R}^p\rightarrow\mathbb{R}\) is unknown in practice and its estimation is the objective of predictive modeling: \(m\) encodes the relation2 between \(Y\) and \(X_1,\ldots,X_p\). In other words, \(m\) captures the trend of the relation between \(Y\) and \(X_1,\ldots,X_p,\) and \(\varepsilon\) represents the stochasticity of that relation. Knowing \(m\) allows to predict \(Y.\) This course is devoted to statistical models3 that allow us to come up with an estimate of \(m,\) denoted by \(\hat m,\) that can be used to predict \(Y.\)
Let’s see a concrete example of this with an artificial dataset. Suppose \(Y\) represents average fuel consumption (l/100km) of a car and \(X\) is the average speed (km/h). It is well-known from physics that the energy and speed have a quadratic relationship, and therefore we may assume that \(Y\) and \(X\) are truly quadratically-related for the sake of exposition:
\[\begin{align*} Y=a+bX+cX^2+\varepsilon. \end{align*}\]
Then \(m:\mathbb{R}\rightarrow\mathbb{R}\) (\(p=1\)) with \(m(x)=a+bx+cx^2.\) Suppose the following data consists of measurements from a given car model, measured in different drivers and conditions (we do not have data for accounting for all those effects, which go to the \(\varepsilon\) term4):
x <- c(64, 20, 14, 64, 44, 39, 25, 53, 48, 9, 100, 112, 78, 105, 116, 94, 71,
71, 101, 109)
y <- c(4, 6, 6.4, 4.1, 4.9, 4.4, 6.6, 4.4, 3.8, 7, 7.4, 8.4, 5.2, 7.6, 9.8,
6.4, 5.1, 4.8, 8.2, 8.7)
plot(x, y, xlab = "Speed", ylab = "Fuel consumption")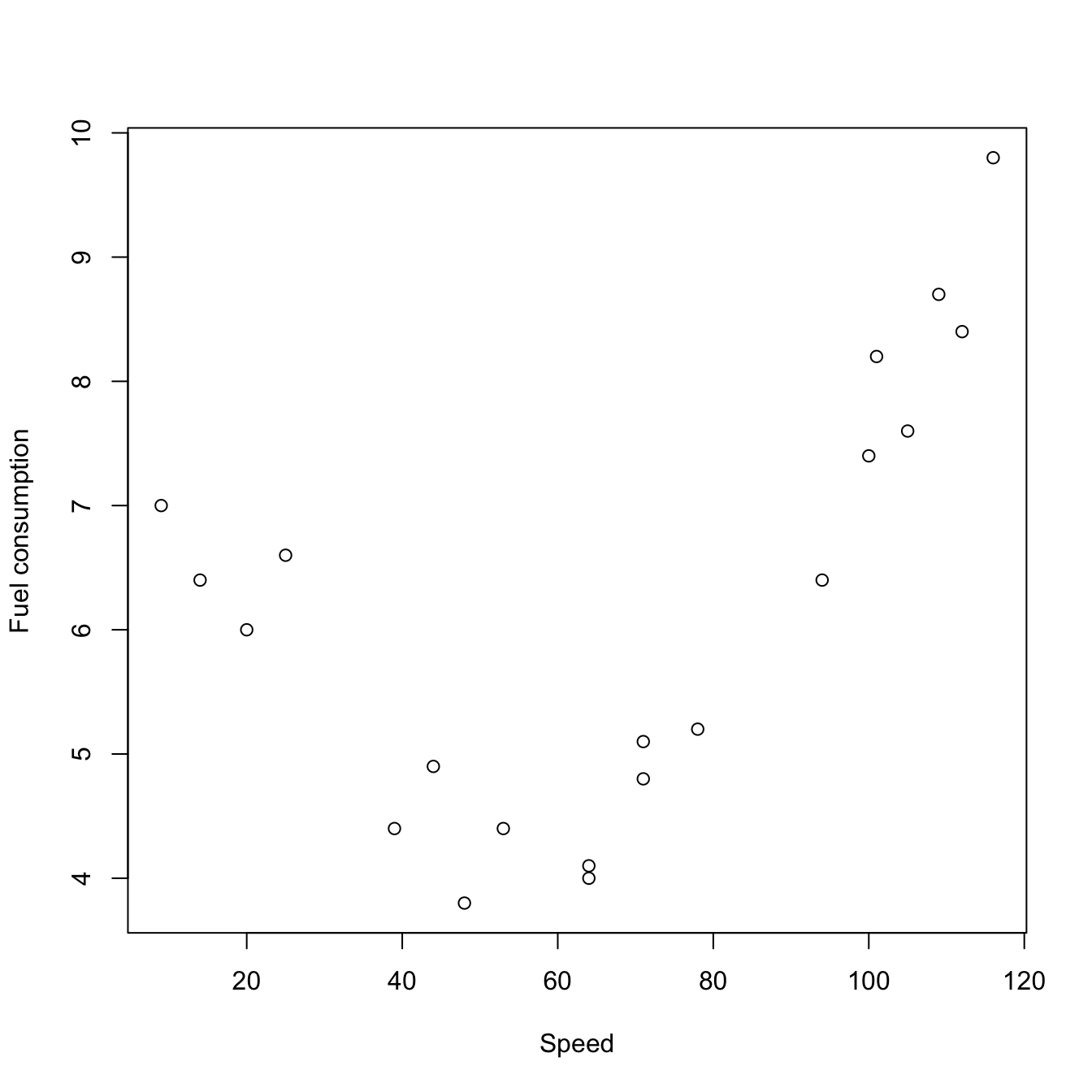
Figure 1.1: Scatterplot of fuel consumption vs. speed.
From this data, we can estimate \(m\) by means of a polynomial model5:
# Estimates for a, b, and c
lm(y ~ x + I(x^2))
##
## Call:
## lm(formula = y ~ x + I(x^2))
##
## Coefficients:
## (Intercept) x I(x^2)
## 8.512421 -0.153291 0.001408Then the estimate of \(m\) is \(\hat m(x)=\hat{a}+\hat{b} x+\hat{c} x^2=8.512-0.153x+0.001x^2\) and its fit to the data is pretty good. As a consequence, we can use this precise mathematical function to predict the \(Y\) from a particular observation \(X.\) For example, the estimated fuel consumption at speed 90 km/h is 8.512421 - 0.153291 * 90 + 0.001408 * 90^2 = 6.1210.
plot(x, y, xlab = "Speed", ylab = "Fuel consumption")
curve(8.512421 - 0.153291 * x + 0.001408 * x^2, add = TRUE, col = 2)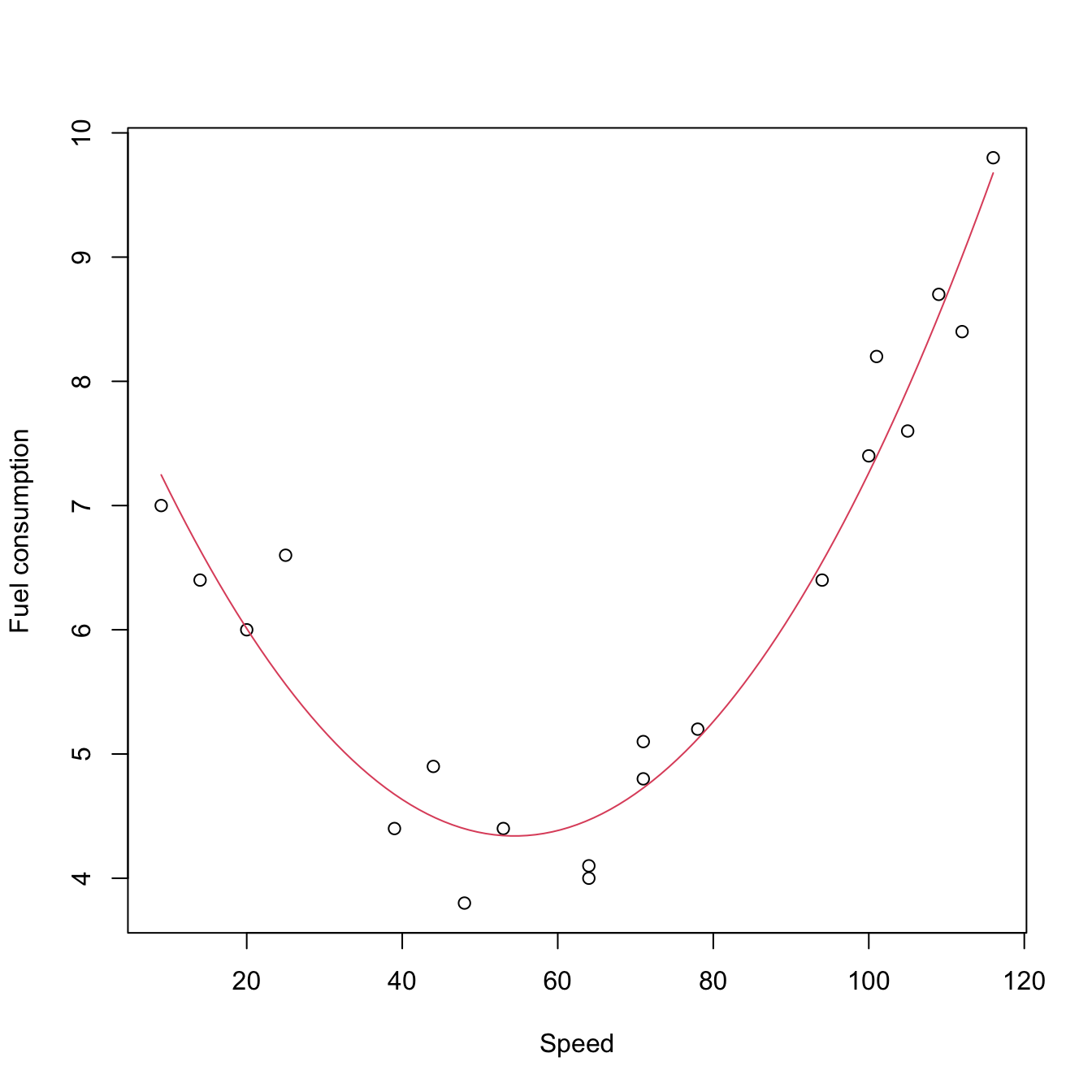
Figure 1.2: Fitted quadratic model.
There are a number of generic issues and decisions to take when building and estimating regression models that are worth to highlight:
The prediction accuracy versus interpretability trade-off. Prediction accuracy is key in any predictive model: of course, the better the model is able to predict \(Y,\) the more useful it will be. However, some models achieve this predictive accuracy in exchange of a clear interpretability of the model (the so-called black boxes). Interpretability is key in order to gain insights on the prediction process, to know exactly which variables are most influential in \(Y,\) to be able to interpret the parameters of the model, and to translate the prediction process to non-experts. In essence, interpretability allows to explain precisely how and why the model behaves when predicting \(Y\) from \(X_1,\ldots,X_p.\) Most of models seen in these notes clearly favor interpretability6 and hence they may make a sacrifice in terms of their prediction accuracy when compared with more convoluted models.
Model correctness versus model usefulness. Correctness and usefulness are two different concepts in modeling. The first refers to the model being statistically correct, this is, it translates to stating that the assumptions on which the model relating \(Y\) with \(X_1,\ldots,X_p\) is built are satisfied. The second refers to the model being useful for explaining or predicting \(Y\) from \(X_1,\ldots,X_p.\) Both concepts are certainly related (if the model is correct/useful, then likely it is useful/correct) but neither is implied by the other. For example, a regression model might be correct but useless if the variance of \(\varepsilon\) is large (too much noise). And yet if the model is not completely correct, it may give useful insights and predictions, but inference may be completely spurious.7
Flexibility versus simplicity. The best model is the one which is very simple (low number of parameters), highly interpretable, and delivers great predictions. This is often unachievable in practice. What can be achieved is a good model: the one that balances the simplicity with the prediction accuracy, which is often increased the more flexible the model is. However, flexibility comes at a price: more flexible (hence more complex) models use more parameters that need to be estimated from a finite amount of information – the sample. This is problematic, as overly flexible models are more dependent on the sample, up to the point in which they end up not estimating the true relation between \(Y\) and \(X_1,\ldots,X_p,\) \(m,\) but merely interpolating the observed data. This well-known phenomenon is called overfitting and it can be avoided by splitting the dataset in two datasets:8 the training dataset, used for estimating the model; and the testing dataset, used for evaluating the fitted model predictive performance. On the other hand, excessive simplicity (underfitting) is also problematic, since the true relation between \(Y\) and \(X_1,\ldots,X_p\) may be overly simplified. Therefore, a trade-off in the degree of flexibility has to be attained for having a good model. This is often referred to as the bias-variance trade-off (low flexibility increases the bias of the fitted model, high flexibility increases the variance). An illustration of this transversal problem in predictive modeling is given in Figure 1.3.
Figure 1.3: Illustration of overfitting in polynomial regression. The left plot shows the training dataset and the right plot the testing dataset. Better fitting of the training data with a higher polynomial order does not imply better performance in new observations (prediction), but just an over-fitting of the available data with an overly-parametrized model (too flexible for the amount of information available). Reduction in the predictive error is only achieved with fits (in red) of polynomial degrees close to the true regression (in black). Application available here.
The relation is encoded in average by means of the conditional expectation.↩︎
That can be regarded as “structures for \(m\)”.↩︎
This is an alternative useful view of \(\varepsilon\): the aggregation of the effects what we cannot account for predicting \(Y.\)↩︎
Note we use the information that \(m\) has to be of a particular form (in this case quadratic) which is an unrealistic situation for other data applications.↩︎
Not only that but they are neatly interpretable.↩︎
Particularly, it usually happens that the inference based on erroneous assumptions underestimates variability, as the assumptions tend to ensure that the information of the sample is maximal for estimating the model at hand. Thus, inference based on erroneous assumptions results in a false sense of confidence: a larger error is made in reality than the one the model theory states.↩︎
Three datasets if we are fitting hyperparameters or tuning parameters in our model: the training dataset for estimating the model parameters; the validation dataset for estimating the hyper-parameters; and the testing dataset for evaluating the final performance of the fitted model.↩︎