Chapter 5 Generalized linear models

As we saw in Chapter 2, linear regression assumes that the response variable \(Y\) is such that

\[\begin{align*} Y|(X_1=x_1,\ldots,X_p=x_p)\sim \mathcal{N}(\beta_0+\beta_1x_1+\cdots+\beta_px_p,\sigma^2) \end{align*}\]

and hence

\[\begin{align*} \mathbb{E}[Y|X_1=x_1,\ldots,X_p=x_p]=\beta_0+\beta_1x_1+\cdots+\beta_px_p. \end{align*}\]

This, in particular, implies that \(Y\) is continuous. In this chapter we will see how generalized linear models can deal with other kinds of distributions for \(Y|(X_1=x_1,\ldots,X_p=x_p),\) particularly with discrete responses, by modeling the transformed conditional expectation. The simplest generalized linear model is logistic regression, which arises when \(Y\) is a binary response, that is, a variable encoding two categories with \(0\) and \(1.\) This model would be useful, for example, to predict \(Y\) given \(X\) from the sample \(\{(X_i,Y_i)\}_{i=1}^n\) in Figure 5.1.

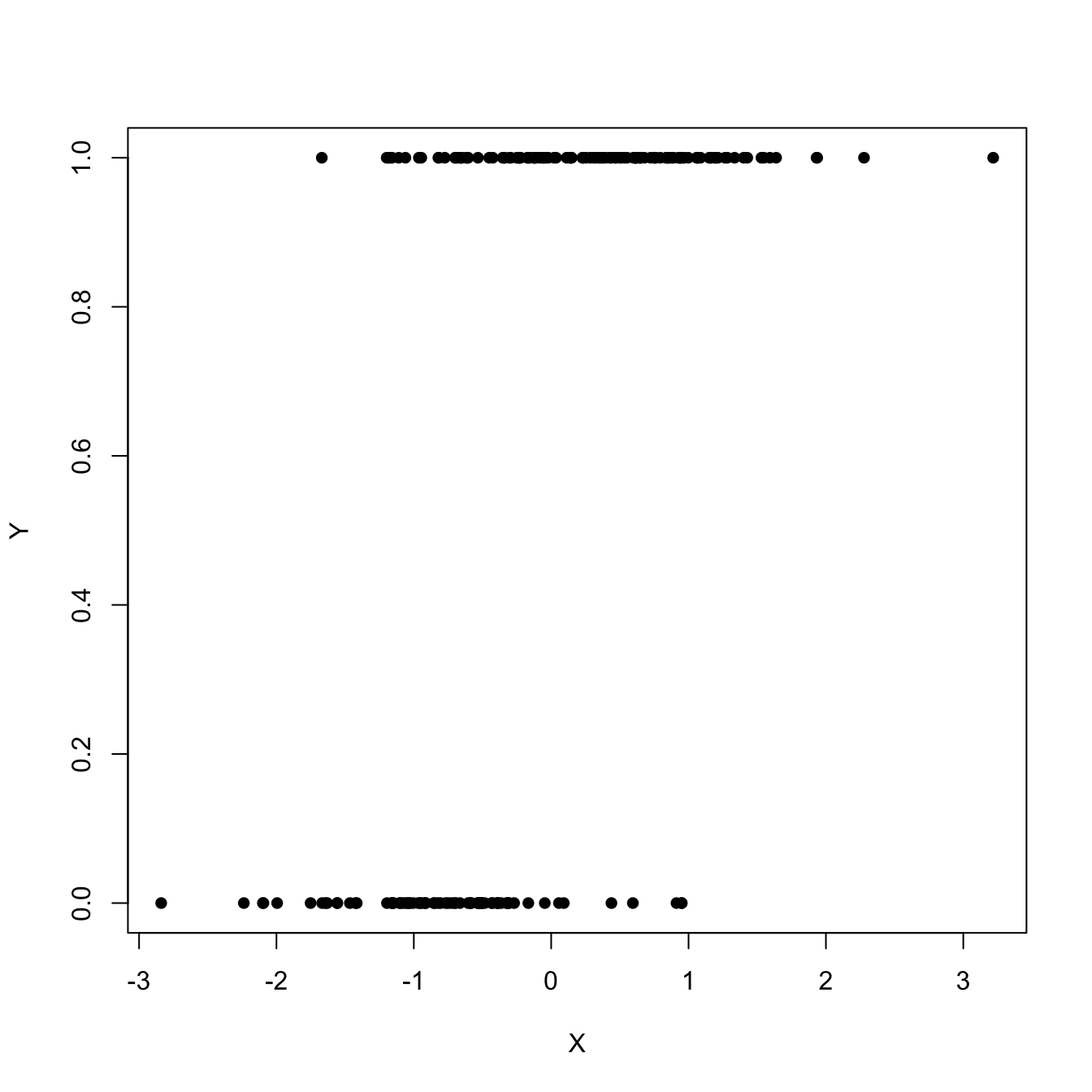
Figure 5.1: Scatterplot of a sample \(\{(X_i,Y_i)\}_{i=1}^n\) sampled from a logistic regression.