A.5 A note of caution with inference after model-selection
Inferences from models that result from model-selection procedures, such as stepwise regression, ridge, or lasso, have to be analyzed with caution. The reason is because we are using the sample twice: one for selecting the most significant / informative predictors in order to be included in the model, and other for making inference using the same sample. While making this, we are biasing the significance tests, and thus obtaining unrealistically small \(p\)-values. In other words, when included in the model, some selected predictors will be shown as significant when in reality they are not.
A relatively simple solution for performing valid inference in a data-driven selected model is to split the dataset in two parts: one part for performing model-selection (selection of important variables and model structure; inside this part we could have two subparts for training and validation) and another for fitting the model and carrying out inference on the coefficients based on that fit. Obviously, this approach has the undesirable consequence of losing power in the estimation and inference parts due to the sample splitting, but it guarantees valid inference in a simple and general way.
The next simulation exercise exemplifies the previous remarks. Consider the following linear model
\[\begin{align} Y=\beta_1X_1+\beta_2X_2+\beta_3X_3+\beta_4X_4+\varepsilon, \end{align}\]
where \(\beta_1=\beta_2=1,\) \(\beta_3=\beta_4=0,\) and \(\varepsilon\sim\mathcal{N}(0,1).\) The next chunk of code analyses the significances of the four coefficients for:
- The model with all the predictors. The inferences for the coefficients are correct: the distribution of the \(p\)-values (
pvalues1) is uniform whenever \(H_0:\beta_j=0\) holds (for \(j=3,4\)) and concentrated around \(0\) when \(H_0\) does not hold (for \(j=1,2\)). - The model with predictors selected by stepwise regression. The inferences for the coefficients are biased: when \(X_3\) and \(X_4\) are included in the model is because they are highly significant for the given sample by mere chance. Therefore, the distribution of the \(p\)-values (
pvalues2) is not uniform but concentrated at \(0.\) - The model with selected predictors by stepwise regression, but fitted in a separate dataset. In this case, the \(p\)-values (
pvalues3) are not unrealistically small if the non-significant predictors are included in the model and the inference is correct.
# Simulation setting
n <- 2e2
p <- 4
p0 <- p %/% 2
beta <- c(rep(1, p0), rep(0, p - p0))
# Generate two sets of independent data following the same linear model
# with coefficients beta and null intercept
x1 <- matrix(rnorm(n * p), nrow = n, ncol = p)
data1 <- data.frame("x" = x1)
xbeta1 <- x1 %*% beta
x2 <- matrix(rnorm(n * p), nrow = n, ncol = p)
data2 <- data.frame("x" = x2)
xbeta2 <- x2 %*% beta
# Objects for the simulation
M <- 1e4
pvalues1 <- pvalues2 <- pvalues3 <- matrix(NA, nrow = M, ncol = p)
set.seed(12345678)
data1$y <- xbeta1 + rnorm(n)
nam <- names(lm(y ~ 0 + ., data = data1)$coefficients)
# Simulation
# pb <- txtProgressBar(style = 3)
for (i in 1:M) {
# Generate new data
data1$y <- xbeta1 + rnorm(n)
# Obtain the significances of the coefficients for the usual linear model
mod1 <- lm(y ~ 0 + ., data = data1)
s1 <- summary(mod1)
pvalues1[i, ] <- s1$coefficients[, 4]
# Obtain the significances of the coefficients for a data-driven selected
# linear model (in this case, by stepwise regression using BIC)
mod2 <- MASS::stepAIC(mod1, k = log(n), trace = 0)
s2 <- summary(mod2)
ind <- match(x = names(s2$coefficients[, 4]), table = nam)
pvalues2[i, ind] <- s2$coefficients[, 4]
# Generate independent data
data2$y <- xbeta2 + rnorm(n)
# Significances of the coefficients by the data-driven selected model
s3 <- summary(lm(y ~ 0 + ., data = data2[, c(ind, p + 1)]))
pvalues3[i, ind] <- s3$coefficients[, 4]
# Progress
# setTxtProgressBar(pb = pb, value = i / M)
}
# Percentage of NA's: NA = predictor excluded
apply(pvalues2, 2, function(x) mean(is.na(x)))
## [1] 0.0000 0.0000 0.9774 0.9766
# Boxplots of significances
boxplot(pvalues1, names = expression(beta[1], beta[3], beta[3], beta[4]),
main = "p-values in the full model", ylim = c(0, 1))
boxplot(pvalues2, names = expression(beta[1], beta[3], beta[3], beta[4]),
main = "p-values in the stepwise model", ylim = c(0, 1))
boxplot(pvalues3, names = expression(beta[1], beta[3], beta[3], beta[4]),
main = "p-values in the model with the predictors selected by
stepwise regression, and fitted in an independent sample",
ylim = c(0, 1))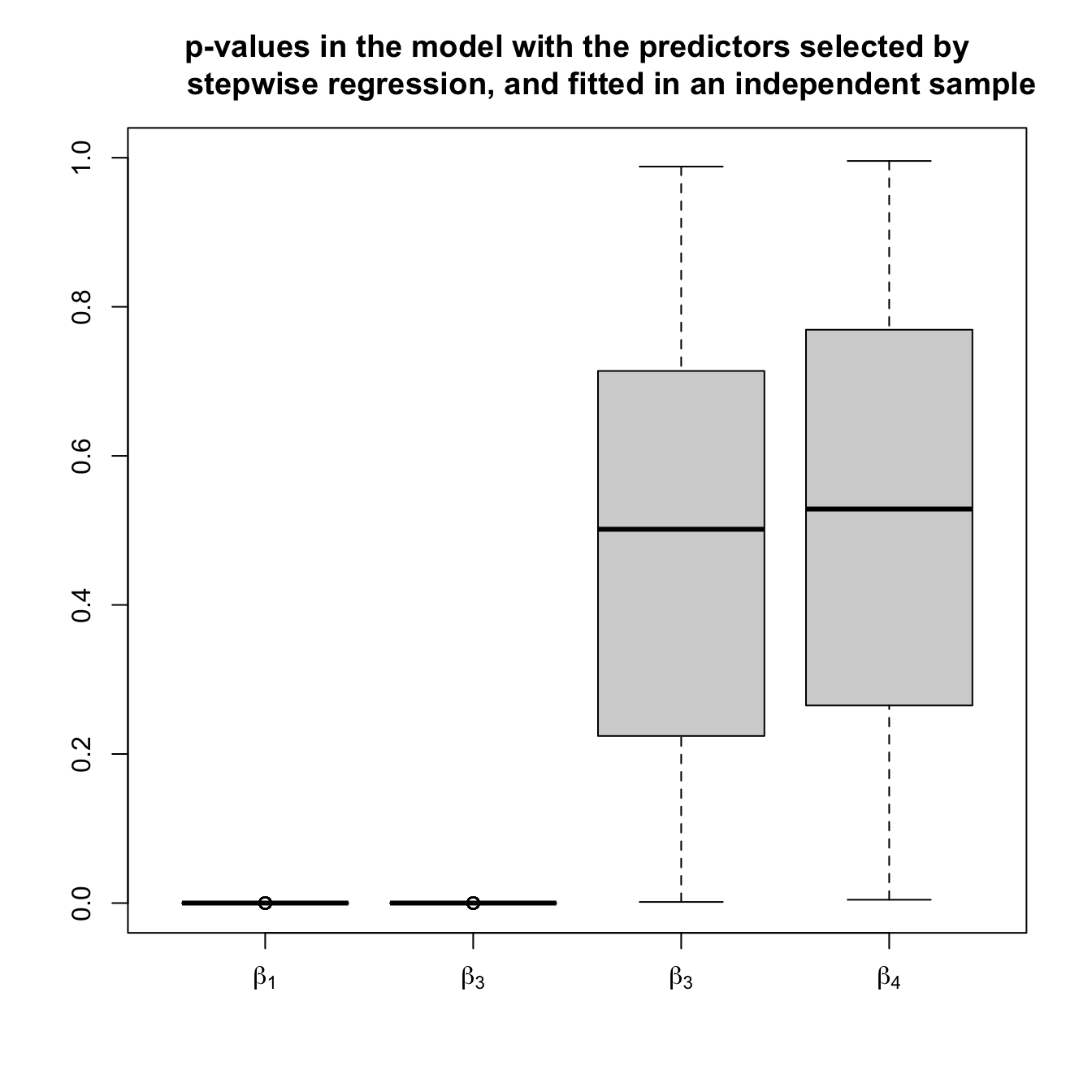
# Test uniformity of the p-values associated to the coefficients that are 0
apply(pvalues1[, (p0 + 1):p], 2, function(x) ks.test(x, y = "punif")$p.value)
## [1] 0.4755784 0.4965309
apply(pvalues2[, (p0 + 1):p], 2, function(x) ks.test(x, y = "punif")$p.value)
## [1] 0 0
apply(pvalues3[, (p0 + 1):p], 2, function(x) ks.test(x, y = "punif")$p.value)
## [1] 0.8322453 0.1940926