4.1 Kernel regression estimation

4.1.1 Nadaraya–Watson estimator

Our objective is to estimate the regression function $m:\mathbb{R}\longrightarrow\mathbb{R}$ nonparametrically. Due to its definition, we can rewrite $m$ in (4.1) as¹¹⁸

\[\begin{align} m(x)=&\,\mathbb{E}[Y| X=x]\nonumber\\ =&\,\int y f_{Y| X=x}(y)\,\mathrm{d}y\nonumber\\ =&\,\frac{\int y f(x,y)\,\mathrm{d}y}{f_X(x)}.\tag{4.2} \end{align}\]

Exercise 4.1 Prove that $\mathbb{E}[m(X)]=\mathbb{E}[Y]$ using Proposition 1.1.

Expression (4.2) shows an interesting point: the regression function can be computed from the joint density $f$ and the marginal $f_X.$ Therefore, given a sample $(X_1,Y_1),\ldots,(X_n,Y_n),$ a nonparametric estimate of $m$ may follow by replacing the previous densities with their kernel density estimators. From the previous section, we know how to do this using the multivariate and univariate kde’s given in (2.7) and (3.1), respectively.

For the multivariate kde, we can consider the kde (3.2) based on product kernels for the two-dimensional case and bandwidths $\mathbf{h}=(h_1,h_2)',$ that is, the estimate

\[\begin{align} \hat{f}(x,y;\mathbf{h})=\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_{i})K_{h_2}(y-Y_{i})\tag{4.3} \end{align}\]

of the joint pdf of $(X,Y).$ Besides, considering the same bandwidth $h_1$ for the kde of $f_X,$ we have

\[\begin{align} \hat{f}_X(x;h_1)=\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_{i}).\tag{4.4} \end{align}\]

We can therefore define the estimator of $m$ that results from replacing $f$ and $f_X$ in (4.2) with (4.3) and (4.4), respectively:

\[\begin{align*} \frac{\int y \hat{f}(x,y;\mathbf{h})\,\mathrm{d}y}{\hat{f}_X(x;h_1)}=&\,\frac{\int y \frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)K_{h_2}(y-Y_i)\,\mathrm{d}y}{\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)}\\ =&\,\frac{\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)\int y K_{h_2}(y-Y_i)\,\mathrm{d}y}{\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)}\\ =&\,\frac{\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)Y_i}{\frac{1}{n}\sum_{i=1}^nK_{h_1}(x-X_i)}\\ =&\,\sum_{i=1}^n\frac{K_{h_1}(x-X_i)}{\sum_{i=1}^nK_{h_1}(x-X_i)}Y_i. \end{align*}\]

The resulting estimator¹¹⁹ is the so-called Nadaraya–Watson¹²⁰ estimator of the regression function:

\[\begin{align} \hat{m}(x;0,h):=\sum_{i=1}^n\frac{K_h(x-X_i)}{\sum_{j=1}^nK_h(x-X_j)}Y_i=\sum_{i=1}^nW^0_{i}(x)Y_i, \tag{4.5} \end{align}\]

where¹²¹

\[\begin{align*} W^0_{i}(x):=\frac{K_h(x-X_i)}{\sum_{j=1}^nK_h(x-X_j)}. \end{align*}\]

The Nadaraya–Watson estimator can be seen as a weighted average of $Y_1,\ldots,Y_n$ by means of the set of weights $\{W_i(x)\}_{i=1}^n$ (they always add to one). The set of varying weights depends on the evaluation point $x.$ That means that the Nadaraya–Watson estimator is a local mean of $Y_1,\ldots,Y_n$ about $X=x$ (see Figure 4.2).

Exercise 4.2 Is it true that the unconditional expectation of $\hat m(x;0,h),$ for any $x,$ is $\mathbb{E}[Y]$? That is, is it true that $\mathbb{E}[\hat m(x;0,h)]=\mathbb{E}[Y]$? Prove or disprove the equality.

Let’s implement the Nadaraya–Watson estimator from scratch to get a feeling of how it works in practice.

# A naive implementation of the Nadaraya-Watson estimator
nw <- function(x, X, Y, h, K = dnorm) {

  # Arguments
  # x: evaluation points
  # X: vector (size n) with the predictor
  # Y: vector (size n) with the response variable
  # h: bandwidth
  # K: kernel

  # Matrix of size n x length(x) (rbind() is called for ensuring a matrix
  # output if x is a scalar)
  Kx <- rbind(sapply(X, function(Xi) K((x - Xi) / h) / h))

  # Weights
  W <- Kx / rowSums(Kx) # Column recycling!

  # Means at x ("drop" to drop the matrix attributes)
  drop(W %*% Y)

}

# Generate some data to test the implementation
set.seed(12345)
n <- 100
eps <- rnorm(n, sd = 2)
m <- function(x) x^2 * cos(x)
# m <- function(x) x - x^2 # Works equally well for other regression function
X <- rnorm(n, sd = 2)
Y <- m(X) + eps
x_grid <- seq(-10, 10, l = 500)

# Bandwidth
h <- 0.5

# Plot data
plot(X, Y)
rug(X, side = 1); rug(Y, side = 2)
lines(x_grid, m(x_grid), col = 1)
lines(x_grid, nw(x = x_grid, X = X, Y = Y, h = h), col = 2)
legend("top", legend = c("True regression", "Nadaraya-Watson"),
       lwd = 2, col = 1:2)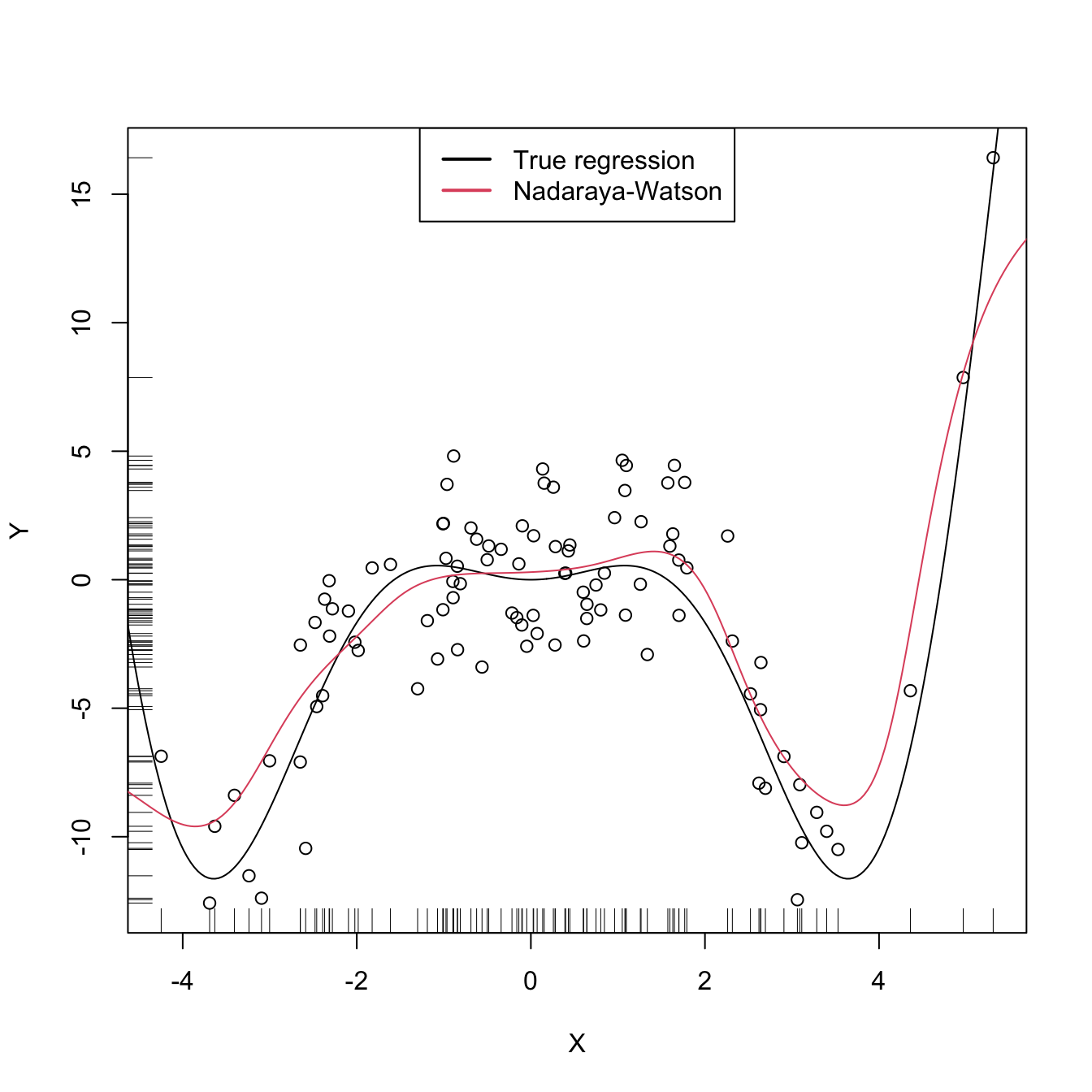

$The Nadaraya–Watson estimator of an arbitrary regression function $m.$ Observe how the Nadaraya–Watson estimator is able to estimate the nonlinear form of the regression function without prior knowledge about its shape.$

Figure 4.1: The Nadaraya–Watson estimator of an arbitrary regression function $m.$ Observe how the Nadaraya–Watson estimator is able to estimate the nonlinear form of the regression function without prior knowledge about its shape.

Exercise 4.3 Implement in R your own version of the Nadaraya–Watson estimator and compare it with the nw function. Focus only on the normal kernel. You may reduce the accuracy of the final computation up to 1e-7 to achieve better efficiency. How much are you able to improve the speed of nw? Use the microbenchmark::microbenchmark function to measure the running times for a sample of size $n=10,000.$

Similarly to kernel density estimation, in the Nadaraya–Watson estimator the bandwidth has a prominent effect on the shape of the estimator, whereas the kernel is clearly less important. The code below illustrates the effect of varying $h$ using the manipulate::manipulate function.

# Simple plot of N-W for varying h's
manipulate::manipulate({

  # Plot data
  plot(X, Y)
  rug(X, side = 1); rug(Y, side = 2)
  lines(x_grid, m(x_grid), col = 1)
  lines(x_grid, nw(x = x_grid, X = X, Y = Y, h = h), col = 2)
  legend("topright", legend = c("True regression", "Nadaraya-Watson"),
         lwd = 2, col = 1:2)

}, h = manipulate::slider(min = 0.01, max = 10, initial = 0.5, step = 0.01))

4.1.2 Local polynomial estimator

The Nadaraya–Watson estimator can be seen as a particular case of a wider class of nonparametric estimators, the so-called local polynomial estimators. Specifically, Nadaraya–Watson is the one that corresponds to performing a local constant fit. Let’s see this wider class of nonparametric estimators and their advantages with respect to the Nadaraya–Watson estimator.

A motivation for the local polynomial fit comes from attempting to find an estimator $\hat{m}$ of $m$ that “minimizes”¹²² the RSS

\[\begin{align} \sum_{i=1}^n(Y_i-\hat{m}(X_i))^2\tag{4.6} \end{align}\]

without assuming any particular form for the underlying $m.$ This is not achievable directly, since no knowledge about $m$ is available. Recall that what it was done in parametric models, such as linear regression (see Section B.1), was to assume a parametrization for $m$ (e.g., $m_{\boldsymbol{\beta}}(\mathbf{x})=\beta_0+\beta_1x$ for the simple linear model) which allowed tackling the minimization of (4.6) by means of solving

\[\begin{align*} m_{\hat{\boldsymbol{\beta}}}(\mathbf{x}):=\arg\min_{\boldsymbol{\beta}}\sum_{i=1}^n(Y_i-m_{\boldsymbol{\beta}}(X_i))^2. \end{align*}\]

When $m$ has no parametrization available and can adopt any mathematical form, an alternative approach is required. The first step is to induce a local parametrization on $m.$ By a $p$-th¹²³ order Taylor expression it is possible to obtain that, for $x$ close to $X_i,$

\[\begin{align} m(X_i)\approx&\, m(x)+m'(x)(X_i-x)+\frac{m''(x)}{2}(X_i-x)^2\nonumber\\ &+\cdots+\frac{m^{(p)}(x)}{p!}(X_i-x)^p.\tag{4.7} \end{align}\]

Then, plugging (4.7) in the population version of (4.6) that replaces $\hat{m}$ with $m,$ we have that

\[\begin{align} \sum_{i=1}^n\left(Y_i-\sum_{j=0}^p\frac{m^{(j)}(x)}{j!}(X_i-x)^j\right)^2.\tag{4.8} \end{align}\]

This expression is still not workable: it depends on $m^{(j)}(x),$ $j=0,\ldots,p,$ which of course are unknown, as $m$ is unknown. The key idea now is:

Set $\beta_j:=\frac{m^{(j)}(x)}{j!}$ and turn (4.8) into a linear regression problem where the unknown parameters are precisely $\boldsymbol{\beta}=(\beta_0,\beta_1,\ldots,\beta_p)'.$

Simply rewriting (4.8) using this idea gives

\[\begin{align} \sum_{i=1}^n\left(Y_i-\sum_{j=0}^p\beta_j(X_i-x)^j\right)^2.\tag{4.9} \end{align}\]

Now, estimates for $\boldsymbol{\beta}$ automatically produce estimates for $m^{(j)}(x),$ $j=0,\ldots,p.$ In addition, we know how to obtain an estimate $\hat{\boldsymbol{\beta}}$ that minimizes (4.9), since this is precisely the least squares problem studied in linear models.¹²⁴ The final touch is to weight the contributions of each datum $(X_i,Y_i)$ to the estimation of $m(x)$ according to the proximity of $X_i$ to $x.$¹²⁵ We can achieve this precisely with kernels:

\[\begin{align} \hat{\boldsymbol{\beta}}_h:=\arg\min_{\boldsymbol{\beta}\in\mathbb{R}^{p+1}}\sum_{i=1}^n\left(Y_i-\sum_{j=0}^p\beta_j(X_i-x)^j\right)^2K_h(x-X_i).\tag{4.10} \end{align}\]

Solving (4.10) is easy once the proper notation is introduced. To that end, denote

\[\begin{align*} \mathbf{X}:=\begin{pmatrix} 1 & X_1-x & \cdots & (X_1-x)^p\\ \vdots & \vdots & \ddots & \vdots\\ 1 & X_n-x & \cdots & (X_n-x)^p\\ \end{pmatrix}_{n\times(p+1)} \end{align*}\]

and

\[\begin{align*} \mathbf{W}:=\mathrm{diag}(K_h(X_1-x),\ldots, K_h(X_n-x)),\quad \mathbf{Y}:=\begin{pmatrix} Y_1\\ \vdots\\ Y_n \end{pmatrix}_{n\times 1}. \end{align*}\]

Then we can re-express (4.10) into a weighted least squares problem, which has an exact solution:

\[\begin{align} \hat{\boldsymbol{\beta}}_h&=\arg\min_{\boldsymbol{\beta}\in\mathbb{R}^{p+1}} (\mathbf{Y}-\mathbf{X}\boldsymbol{\beta})'\mathbf{W}(\mathbf{Y}-\mathbf{X}\boldsymbol{\beta})\tag{4.11}\\ &=(\mathbf{X}'\mathbf{W}\mathbf{X})^{-1}\mathbf{X}'\mathbf{W}\mathbf{Y}.\tag{4.12} \end{align}\]

The estimate¹²⁶ of $m(x)$ is therefore computed as¹²⁷

\[\begin{align} \hat{m}(x;p,h):=&\,\hat{\beta}_{h,0}\nonumber\\ =&\,\mathbf{e}_1'(\mathbf{X}'\mathbf{W}\mathbf{X})^{-1}\mathbf{X}'\mathbf{W}\mathbf{Y}\nonumber\\ =&\,\sum_{i=1}^nW^p_{i}(x)Y_i,\tag{4.13} \end{align}\]

where

\[\begin{align*} W^p_{i}(x):=\mathbf{e}_1'(\mathbf{X}'\mathbf{W}\mathbf{X})^{-1}\mathbf{X}'\mathbf{W}\mathbf{e}_i \end{align*}\]

and $\mathbf{e}_i$ is the $i$-th canonical vector.¹²⁸ Just as the Nadaraya–Watson was, the local polynomial estimator is a weighted linear combination of the responses.¹²⁹

Two cases on (4.13) deserve special attention:

$p=0$ is the local constant estimator, previously referred to as the Nadaraya–Watson estimator. In this situation, the estimator has explicit weights, as we saw before:

\[\begin{align} W_i^0(x)=\frac{K_h(x-X_i)}{\sum_{j=1}^nK_h(x-X_j)}.\tag{4.14} \end{align}\]
$p=1$ is the local linear estimator, which has weights equal to

\[\begin{align} W_i^1(x)=\frac{1}{n}\frac{\hat{s}_2(x;h)-\hat{s}_1(x;h)(X_i-x)}{\hat{s}_2(x;h)\hat{s}_0(x;h)-\hat{s}_1(x;h)^2}K_h(x-X_i),\tag{4.15} \end{align}\]

where $\hat{s}_r(x;h):=\frac{1}{n}\sum_{i=1}^n(X_i-x)^rK_h(x-X_i).$

Exercise 4.4 Show that (4.12) is the solution of (4.11), $\hat{\boldsymbol{\beta}}_h.$ To do so, first prove Exercise B.1.

Exercise 4.5 Show that the local polynomial estimator yields the Nadaraya–Watson estimator when $p=0.$ Use (4.12) to obtain (4.5).

Exercise 4.6 Prove that:

$\sum_{i=1}^nW_i^0(x)=1$ and $W_i^0(x)\geq0$ for all $i=1,\ldots,n$ (weighted mean).
$\sum_{i=1}^nW_i^1(x)=1$ and $W_i^1(x)\not\geq0$ for all $i=1,\ldots,n$ (not a weighted mean). Give an example of positive and negative weights.

Exercise 4.7 Obtain the weight expressions (4.15) of the local linear estimator using the matrix inversion formula for $2\times2$ matrices: $\begin{pmatrix}a & b\\ c & d\end{pmatrix}^{-1}=(ad-bc)^{-1}\begin{pmatrix}d & -b\\ -c & a\end{pmatrix}.$

Remark. The local polynomial fit is computationally more expensive than the local constant fit: $\hat{m}(x;p,h)$ is obtained as the solution of a weighted linear problem, whereas $\hat{m}(x;0,h)$ can directly be computed as a weighted mean of the responses. Even if the explicit form (4.15) is available when $p=1,$ (4.15) is roughly three times more costly than (4.14) (recall the $\hat{s}_r(x;h),$ $r=0,1,2$). The computational demand escalates with $p,$ since computing $\hat{m}(x;p,h)$ requires inverting the $p\times p$ matrix $\mathbf{X}'\mathbf{W}\mathbf{X}.$

The local polynomial estimator $\hat{m}(\cdot;p,h)$ of $m$ performs a series of weighted polynomial fits, as many as points $x$ on which $\hat{m}(\cdot;p,h)$ is to be evaluated.

Figure 4.2 illustrates the construction of the local polynomial estimator (up to cubic degree) and shows how $\hat\beta_0=\hat{m}(x;p,h),$ the intercept of the local fit, estimates $m$ at $x$ by constructing a local polynomial fit in the neighborhood of $x.$

Figure 4.2: Construction of the local polynomial estimator. The animation shows how local polynomial fits in a neighborhood of $x$ are combined to provide an estimate of the regression function, which depends on the polynomial degree, bandwidth, and kernel (gray density at the bottom). The data points are shaded according to their weights for the local fit at $x.$ Application available here.

An inefficient implementation of the local polynomial estimator can be done relatively straightforwardly from the previous insights and from expression (4.12). However, several R packages provide implementations, such as KernSmooth::locpoly and R’s loess¹³⁰ (but this one has a different control of the bandwidth plus a set of other modifications). Below are some examples of their use.

# Generate some data
set.seed(123456)
n <- 100
eps <- rnorm(n, sd = 2)
m <- function(x) x^3 * sin(x)
X <- rnorm(n, sd = 1.5)
Y <- m(X) + eps
x_grid <- seq(-10, 10, l = 500)

# KernSmooth::locpoly fits
h <- 0.25
lp0 <- KernSmooth::locpoly(x = X, y = Y, bandwidth = h, degree = 0,
                           range.x = c(-10, 10), gridsize = 500)
lp1 <- KernSmooth::locpoly(x = X, y = Y, bandwidth = h, degree = 1,
                           range.x = c(-10, 10), gridsize = 500)
# Provide the evaluation points through range.x and gridsize

# loess fits
span <- 0.25 # The default span is 0.75, which works very bad in this scenario
lo0 <- loess(Y ~ X, degree = 0, span = span)
lo1 <- loess(Y ~ X, degree = 1, span = span)
# loess employs a "span" argument that plays the role of a variable bandwidth
# "span" gives the proportion of points of the sample that are taken into
# account for performing the local fit about x and then uses a triweight kernel
# (not a normal kernel) for weighting the contributions. Therefore, the final
# estimate differs from the definition of local polynomial estimator, although
# the principles in which are based are the same

# Prediction at x = 2
x <- 2
lp1$y[which.min(abs(lp1$x - x))] # Prediction by KernSmooth::locpoly
## [1] 5.445975
predict(lo1, newdata = data.frame(X = x)) # Prediction by loess
##        1 
## 5.379652
m(x) # True regression
## [1] 7.274379

# Plot data
plot(X, Y)
rug(X, side = 1); rug(Y, side = 2)
lines(x_grid, m(x_grid), col = 1)
lines(lp0$x, lp0$y, col = 2)
lines(lp1$x, lp1$y, col = 3)
lines(x_grid, predict(lo0, newdata = data.frame(X = x_grid)), col = 2, lty = 2)
lines(x_grid, predict(lo1, newdata = data.frame(X = x_grid)), col = 3, lty = 2)
legend("bottom", legend = c("True regression", "Local constant (locpoly)",
                            "Local linear (locpoly)", "Local constant (loess)",
                            "Local linear (loess)"),
       lwd = 2, col = c(1:3, 2:3), lty = c(rep(1, 3), rep(2, 2)))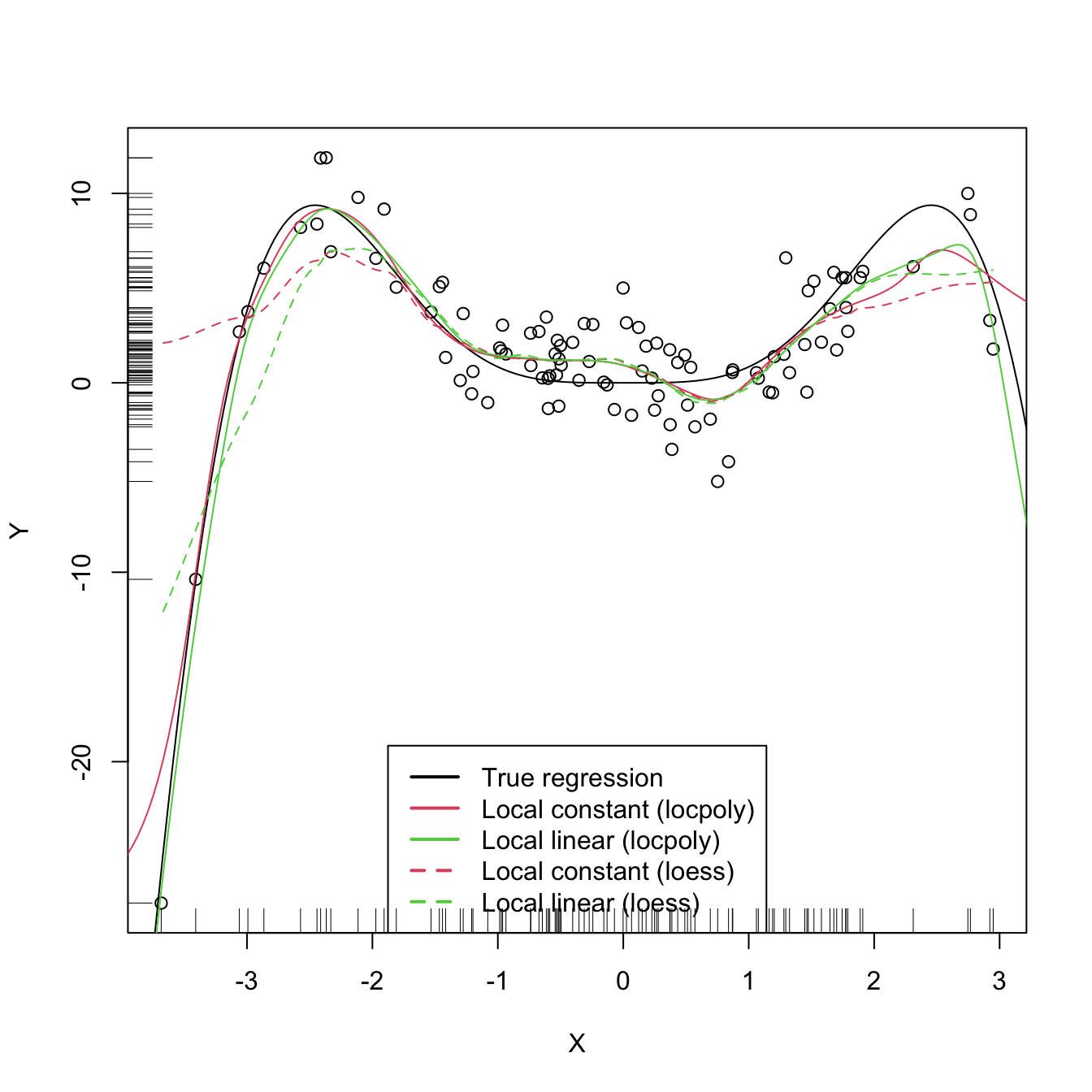

Exercise 4.8 Perform the following tasks:

Implement your own version of the local linear estimator. The function must take a sample X, a sample Y, the points x at which the estimate is to be obtained, the bandwidth h, and the kernel K.
Test its correct behavior by estimating an artificial dataset (e.g., the one considered in Exercise 4.16) that follows a linear model.

As with the Nadaraya–Watson, the local polynomial estimator heavily depends on $h.$

# Simple plot of local polynomials for varying h's
manipulate::manipulate({

  # Plot data
  lpp <- KernSmooth::locpoly(x = X, y = Y, bandwidth = h, degree = p,
                             range.x = c(-10, 10), gridsize = 500)
  plot(X, Y)
  rug(X, side = 1); rug(Y, side = 2)
  lines(x_grid, m(x_grid), col = 1)
  lines(lpp$x, lpp$y, col = p + 2)
  legend("bottom", legend = c("True regression", "Local polynomial fit"),
         lwd = 2, col = c(1, p + 2))

}, p = manipulate::slider(min = 0, max = 4, initial = 0, step = 1),
h = manipulate::slider(min = 0.01, max = 10, initial = 0.5, step = 0.01))

A more sophisticated framework for performing nonparametric estimation of the regression function is the np package, which is introduced in detail in Section 4.5. This package will be the approach chosen for the more challenging situation in which several predictors are present, since the former implementations (KernSmooth::locpoly, loess, and our own implementations) do not scale well for more than one predictor.

Exercise 4.9 Perform the following tasks:

Code your own implementation of the local cubic estimator. The function must take as input the vector of evaluation points x, the sample data, and the bandwidth h. Use the normal kernel. The result must be a vector of the same length as x containing the estimator evaluated at x.
Test the implementation by estimating the regression function in the location model $Y = m(X)+\varepsilon,$ where $m(x)=(x-1)^2,$ $X\sim\mathcal{N}(1,1),$ and $\varepsilon\sim\mathcal{N}(0,0.5).$ Do it for a sample of size $n=500.$

References

Nadaraya, E. A. 1964. “On Estimating Regression.” Teoriya Veroyatnostei i Ee Primeneniya 9 (1): 157–59. https://doi.org/10.1137/1109020.

Watson, G. S. 1964. “Smooth Regression Analysis.” Sankhyā, Series A 26 (4): 359–72. https://www.jstor.org/stable/25049340.

Observe that in the third equality we use that $(X,Y)$ is continuous to motivate the construction of the estimator.↩︎
Notice that the estimator does not depend on $h_2;$ rather, it depends on $h_1,$ the bandwidth employed for smoothing $X.$↩︎
Termed due to the coetaneous proposals by Nadaraya (1964) and Watson (1964). Also known as the local-constant estimators for reasons explained next.↩︎
The change of the sum in the denominator from $\sum_{i=1}^n$ to $\sum_{j=1}^n$ is aimed to avoid confusions with the numerator.↩︎
Obviously, avoiding the spurious perfect fit attained with $\hat{m}(X_i):=Y_i,$ $i=1,\ldots,n.$↩︎
Here we employ $p$ to denote the order of the Taylor expansion (Theorem 1.11) and, correspondingly, the order of the associated polynomial fit. Do not confuse $p$ with the number of original predictors for explaining $Y$ – there is one predictor only, $X.$ However, with a local polynomial fit we expand this predictor to $p$ predictors based on $(X^1,X^2,\ldots,X^p).$↩︎
See (B.4) in Section B.1.1.↩︎
The rationale is simple: $(X_i,Y_i)$ should be more informative about $m(x)$ than $(X_j,Y_j)$ if $x$ and $X_i$ are closer than $x$ and $X_j.$↩︎
Recall that the entries of $\hat{\boldsymbol{\beta}}_h$ are estimating $\boldsymbol{\beta}=\left(m(x), m'(x),\frac{m''(x)}{2},\ldots,\frac{m^{(p)}(x)}{p!}\right)',$ so we are indeed estimating $m(x)$ (first entry) and, in addition, its derivatives up to order $p.$↩︎
An alternative and useful view is that, by minimizing (4.10), we are fitting the linear model $\hat{m}_x(t):=\hat{\beta}_{h,0}+\hat{\beta}_{h,1}(t-x)+\cdots+\hat{\beta}_{h,p}(t-x)^p$ that is centered about $x.$ Then, we employ this model to predict $Y$ for $X=t=x,$ resulting $\hat{\beta}_{h,0}.$↩︎
That is, the entries of $\mathbf{e}_i$ are all zero except for the $i$-th one, which is $1.$↩︎
Which is not a weighted mean in general, only if $p=0;$ see Exercise 4.6.↩︎
The lowess estimator, related to loess, is the one employed in R’s panel.smooth, which is the function in charge of displaying the smooth fits in lm and glm regression diagnostics (employing a prefixed and not data-driven smoothing span of $2/3$ – which makes it inevitably a bad choice for certain data patterns).↩︎