1.1 Probability review

1.1.1 Random variables

A triple $(\Omega,\mathcal{A},\mathbb{P})$ is called a probability space. $\Omega$ represents the sample space, the set of all possible individual outcomes of a random experiment. $\mathcal{A}$ is a $\sigma$-field, a class of subsets of $\Omega$ that is closed under complementation and numerable unions, and such that $\Omega\in\mathcal{A}.$ $\mathcal{A}$ represents the collection of possible events (combinations of individual outcomes) that are assigned a probability by the probability measure $\mathbb{P}.$ A random variable is a map $X:\Omega\longrightarrow\mathbb{R}$ such that $X^{-1}((-\infty,x])=\{\omega\in\Omega:X(\omega)\leq x\}\in\mathcal{A},$ $\forall x\in\mathbb{R}$ (the set $X^{-1}((-\infty,x])$ of possible outcomes of $X$ is said measurable).

1.1.2 Cumulative distribution and probability density functions

The cumulative distribution function (cdf) of a random variable $X$ is $F(x):=\mathbb{P}[X\leq x].$ When an independent and identically distributed (iid) sample $X_1,\ldots,X_n$ is given, the cdf can be estimated by the empirical distribution function (ecdf)

$$\begin{align} F_n(x)=\frac{1}{n}\sum_{i=1}^n1_{\{X_i\leq x\}}, \tag{1.1} \end{align}$$

where $1_A:=\begin{cases}1,&A\text{ is true},\\0,&A\text{ is false}\end{cases}$ is an indicator function.²

Continuous random variables are characterized by either the cdf $F$ or the probability density function (pdf) $f=F',$ the latter representing the infinitesimal relative probability of $X$ per unit of length. We write $X\sim F$ (or $X\sim f$) to denote that $X$ has a cdf $F$ (or a pdf $f$). If two random variables $X$ and $Y$ have the same distribution, we write $X\stackrel{d}{=}Y.$

1.1.3 Expectation

The expectation operator is constructed using the Riemann–Stieltjes “$\,\mathrm{d}F(x)$” integral.³ Hence, for $X\sim F,$ the expectation of $g(X)$ is

$$\begin{align*} \mathbb{E}[g(X)]:=&\,\int g(x)\,\mathrm{d}F(x)\\ =&\, \begin{cases} \displaystyle\int g(x)f(x)\,\mathrm{d}x,&\text{ if }X\text{ is continuous,}\\\displaystyle\sum_{\{x\in\mathbb{R}:\mathbb{P}[X=x]>0\}} g(x)\mathbb{P}[X=x],&\text{ if }X\text{ is discrete.} \end{cases} \end{align*}$$

Unless otherwise stated, the integration limits of any integral are $\mathbb{R}$ or $\mathbb{R}^p.$ The variance operator is defined as $\mathbb{V}\mathrm{ar}[X]:=\mathbb{E}[(X-\mathbb{E}[X])^2].$

1.1.4 Random vectors, marginals, and conditionals

We employ bold face to denote vectors, assumed to be column matrices, and matrices. A $p$-random vector is a map $\mathbf{X}:\Omega\longrightarrow\mathbb{R}^p,$ $\mathbf{X}(\omega):=(X_1(\omega),\ldots,X_p(\omega))',$ such that each $X_i$ is a random variable. The (joint) cdf of $\mathbf{X}$ is $F(\mathbf{x}):=\mathbb{P}[\mathbf{X}\leq \mathbf{x}]:=\mathbb{P}[X_1\leq x_1,\ldots,X_p\leq x_p]$ and, if $\mathbf{X}$ is continuous, its (joint) pdf is $f:=\frac{\partial^p}{\partial x_1\cdots\partial x_p}F.$

The marginals of $F$ and $f$ are the cdfs and pdfs of $X_i,$ $i=1,\ldots,p,$ respectively. They are defined as

$$\begin{align*} F_{X_i}(x_i)&:=\mathbb{P}[X_i\leq x_i]=F(\infty,\ldots,\infty,x_i,\infty,\ldots,\infty),\\ f_{X_i}(x_i)&:=\frac{\partial}{\partial x_i}F_{X_i}(x_i)=\int_{\mathbb{R}^{p-1}} f(\mathbf{x})\,\mathrm{d}\mathbf{x}_{-i}, \end{align*}$$

where $\mathbf{x}_{-i}:=(x_1,\ldots,x_{i-1},x_{i+1},\ldots,x_p)'.$ The definitions can be extended analogously to the marginals of the cdf and pdf of different subsets of $\mathbf{X}.$

The conditional cdf and pdf of $X_1\vert(X_2,\ldots,X_p)$ are defined, respectively, as

$$\begin{align*} F_{X_1\vert \mathbf{X}_{-1}=\mathbf{x}_{-1}}(x_1)&:=\mathbb{P}[X_1\leq x_1\vert \mathbf{X}_{-1}=\mathbf{x}_{-1}],\\ f_{X_1\vert \mathbf{X}_{-1}=\mathbf{x}_{-1}}(x_1)&:=\frac{f(\mathbf{x})}{f_{\mathbf{X}_{-1}}(\mathbf{x}_{-1})}. \end{align*}$$

The conditional expectation of $Y| X$ is the following random variable⁴

$$\begin{align*} \mathbb{E}[Y\vert X]:=\int y \,\mathrm{d}F_{Y\vert X}(y\vert X). \end{align*}$$

The conditional variance of $Y|X$ is defined as

$$\begin{align*} \mathbb{V}\mathrm{ar}[Y\vert X]:=\mathbb{E}[(Y-\mathbb{E}[Y\vert X])^2\vert X]=\mathbb{E}[Y^2\vert X]-\mathbb{E}[Y\vert X]^2. \end{align*}$$

Proposition 1.1 (Laws of total expectation and variance) Let $X$ and $Y$ be two random variables.

• Total expectation: if $\mathbb{E}[|Y|]<\infty,$ then $\mathbb{E}[Y]=\mathbb{E}[\mathbb{E}[Y\vert X]].$
• Total variance: if $\mathbb{E}[Y^2]<\infty,$ then $\mathbb{V}\mathrm{ar}[Y]=\mathbb{E}[\mathbb{V}\mathrm{ar}[Y\vert X]]+\mathbb{V}\mathrm{ar}[\mathbb{E}[Y\vert X]].$

Exercise 1.1 Prove the law of total variance from the law of total expectation.

Figure 1.1 graphically summarizes the concepts of joint, marginal, and conditional distributions within the context of a $2$-dimensional normal.

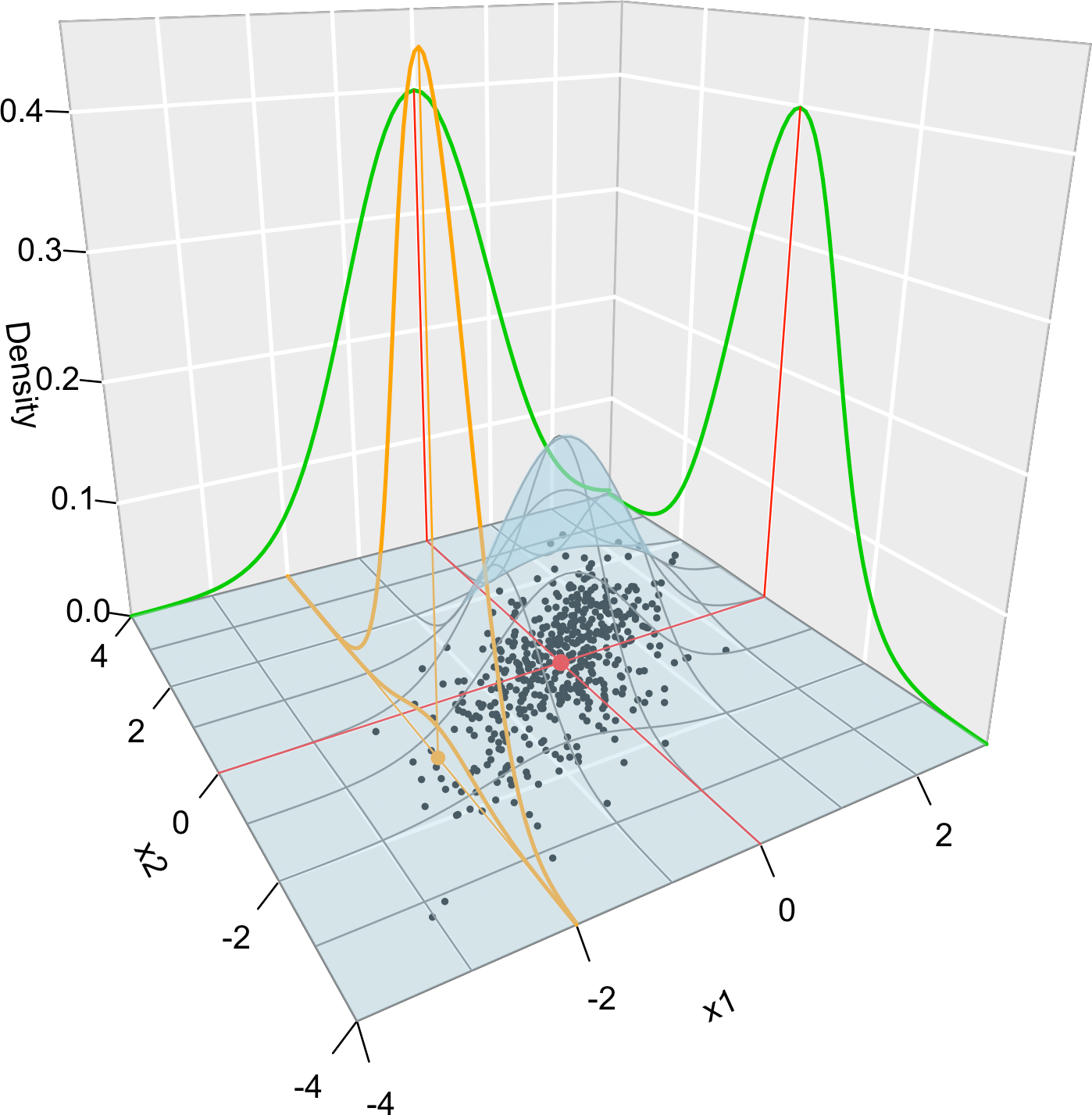
Figure 1.1: Visualization of the joint pdf (in blue), marginal pdfs (green), conditional pdf of $X_2| X_1=x_1$ (orange), expectation (red point), and conditional expectation $\mathbb{E}\lbrack X_2 | X_1=x_1 \rbrack$ (orange point) of a $2$-dimensional normal. The conditioning point of $X_1$ is $x_1=-2.$ Note the different scales of the densities, as they have to integrate one over different supports. Note how the conditional density (upper orange curve) is not the joint pdf $f(x_1,x_2)$ (lower orange curve) with $x_1=-2$ but its rescaling by $\frac{1}{f_{X_1}(x_1)}.$ The parameters of the $2$-dimensional normal are $\mu_1=\mu_2=0,$ $\sigma_1=\sigma_2=1$ and $\rho=0.75$ (see Exercise 1.9). $500$ observations sampled from the distribution are shown in black.

Exercise 1.2 Consider the random vector $(X,Y)$ with joint pdf $$\begin{align*} f(x,y)=\begin{cases} y e^{-a x y},&x>0,\,y\in(0, b),\\ 0,&\text{else.} \end{cases} \end{align*}$$

1. Determine the value of $b>0$ that makes $f$ a valid pdf.
2. Compute $\mathbb{E}[X]$ and $\mathbb{E}[Y].$
3. Verify the law of the total expectation.
4. Verify the law of the total variance.

Exercise 1.3 Consider the continuous random vector $(X_1,X_2)$ with joint pdf given by

$$\begin{align*} f(x_1,x_2)=\begin{cases} 2,&0<x_1<x_2<1,\\ 0,&\mathrm{else.} \end{cases} \end{align*}$$

1. Check that $f$ is a proper pdf.
2. Obtain the joint cdf of $(X_1,X_2).$
3. Obtain the marginal pdfs of $X_1$ and $X_2.$
4. Obtain the marginal cdfs of $X_1$ and $X_2.$
5. Obtain the conditional pdfs of $X_1|X_2=x_2$ and $X_2|X_1=x_1.$

1.1.5 Variance-covariance matrix

For two random variables $X_1$ and $X_2,$ the covariance between them is defined as

$$\begin{align*} \mathrm{Cov}[X_1,X_2]:=\mathbb{E}[(X_1-\mathbb{E}[X_1])(X_2-\mathbb{E}[X_2])]=\mathbb{E}[X_1X_2]-\mathbb{E}[X_1]\mathbb{E}[X_2], \end{align*}$$

and the correlation between them, as

$$\begin{align*} \mathrm{Cor}[X_1,X_2]:=\frac{\mathrm{Cov}[X_1,X_2]}{\sqrt{\mathbb{V}\mathrm{ar}[X_1]\mathbb{V}\mathrm{ar}[X_2]}}. \end{align*}$$

The variance and the covariance are extended to a random vector $\mathbf{X}=(X_1,\ldots,X_p)'$ by means of the so-called variance-covariance matrix:

$$\begin{align*} \mathbb{V}\mathrm{ar}[\mathbf{X}]:=&\,\mathbb{E}[(\mathbf{X}-\mathbb{E}[\mathbf{X}])(\mathbf{X}-\mathbb{E}[\mathbf{X}])']\\ =&\,\mathbb{E}[\mathbf{X}\mathbf{X}']-\mathbb{E}[\mathbf{X}]\mathbb{E}[\mathbf{X}]'\\ =&\,\begin{pmatrix} \mathbb{V}\mathrm{ar}[X_1] & \mathrm{Cov}[X_1,X_2] & \cdots & \mathrm{Cov}[X_1,X_p]\\ \mathrm{Cov}[X_2,X_1] & \mathbb{V}\mathrm{ar}[X_2] & \cdots & \mathrm{Cov}[X_2,X_p]\\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{Cov}[X_p,X_1] & \mathrm{Cov}[X_p,X_2] & \cdots & \mathbb{V}\mathrm{ar}[X_p]\\ \end{pmatrix}, \end{align*}$$

where $\mathbb{E}[\mathbf{X}]:=(\mathbb{E}[X_1],\ldots,\mathbb{E}[X_p])'$ is just the componentwise expectation. As in the univariate case, the expectation is a linear operator, which now means that

$$\begin{align} \mathbb{E}[\mathbf{A}\mathbf{X}+\mathbf{b}]=\mathbf{A}\mathbb{E}[\mathbf{X}]+\mathbf{b},\quad\text{for a $q\times p$ matrix } \mathbf{A}\text{ and }\mathbf{b}\in\mathbb{R}^q.\tag{1.2} \end{align}$$

It follows from (1.2) that

$$\begin{align} \mathbb{V}\mathrm{ar}[\mathbf{A}\mathbf{X}+\mathbf{b}]=\mathbf{A}\mathbb{V}\mathrm{ar}[\mathbf{X}]\mathbf{A}',\quad\text{for a $q\times p$ matrix } \mathbf{A}\text{ and }\mathbf{b}\in\mathbb{R}^q.\tag{1.3} \end{align}$$

1.1.6 Inequalities

We conclude this section by reviewing some useful probabilistic inequalities.

Proposition 1.2 (Markov's inequality) Let $X$ be a nonnegative random variable with $\mathbb{E}[X]<\infty.$ Then

$$\begin{align*} \mathbb{P}[X\geq t]\leq\frac{\mathbb{E}[X]}{t}, \quad\forall t>0. \end{align*}$$

Proposition 1.3 (Chebyshev's inequality) Let $X$ be a random variable with $\mu=\mathbb{E}[X]$ and $\sigma^2=\mathbb{V}\mathrm{ar}[X]<\infty.$ Then

$$\begin{align*} \mathbb{P}[|X-\mu|\geq t]\leq\frac{\sigma^2}{t^2},\quad \forall t>0. \end{align*}$$

Exercise 1.4 Prove Markov’s inequality using $X=X1_{\{X\geq t\}}+X1_{\{X< t\}}.$

Exercise 1.5 Prove Chebyshev’s inequality using Markov’s.

Remark. Chebyshev’s inequality gives a quick and handy way of computing confidence intervals for the values of any random variable $X$ with finite variance:

$$\begin{align} \mathbb{P}[X\in(\mu-t\sigma, \mu+t\sigma)]\geq 1-\frac{1}{t^2},\quad \forall t>0.\tag{1.4} \end{align}$$

That is, for any $t>0,$ the interval $(\mu-t\sigma, \mu+t\sigma)$ has, at least, a probability $1-1/t^2$ of containing a random realization of $X.$ The intervals are conservative, but extremely general. The table below gives the guaranteed coverage probability $1-1/t^2$ for common values of $t.$

$t$	$2$	$3$	$4$	$5$	$6$
Guaranteed coverage	$0.75$	$0.8889$	$0.9375$	$0.96$	$0.9722$

Exercise 1.6 Prove (1.4) from Chebyshev’s inequality.

Proposition 1.4 (Cauchy–Schwartz inequality) Let $X$ and $Y$ such that $\mathbb{E}[X^2]<\infty$ and $\mathbb{E}[Y^2]<\infty.$ Then

$$\begin{align*} |\mathbb{E}[XY]|\leq\sqrt{\mathbb{E}[X^2]\mathbb{E}[Y^2]}. \end{align*}$$

Exercise 1.7 Prove Cauchy–Schwartz inequality “pulling a rabbit out of a hat”: consider the polynomial $p(t)=\mathbb{E}[(tX+Y)^2]=At^2+2Bt+C\geq0,$ $\forall t\in\mathbb{R}.$

Exercise 1.8 Does $\mathbb{E}[|XY|]\leq\sqrt{\mathbb{E}[X^2]\mathbb{E}[Y^2]}$ hold? Observe that, due to the next proposition, $|\mathbb{E}[XY]|\leq \mathbb{E}[|XY|].$

Proposition 1.5 (Jensen's inequality) If $g$ is a convex function, then

$$\begin{align*} g(\mathbb{E}[X])\leq\mathbb{E}[g(X)]. \end{align*}$$

Example 1.1 Jensen’s inequality has interesting derivations. For example:

1. Take $h=-g.$ Then $h$ is a concave function and $h(\mathbb{E}[X])\geq\mathbb{E}[h(X)].$
2. Take $g(x)=x^r$ for $r\geq 1,$ which is a convex function. Then $\mathbb{E}[X]^r\leq \mathbb{E}[X^r].$ If $0<r<1,$ then $g(x)=x^r$ is concave and $\mathbb{E}[X]^r\geq \mathbb{E}[X^r].$
3. The previous results hold considering $g(x)=|x|^r.$ In particular, $|\mathbb{E}[X]|^r\leq \mathbb{E}[|X|^r]$ for $r\geq 1.$
4. Consider $0\leq r\leq s.$ Then $g(x)=x^{s/r}$ is convex (since $s/r\geq 1$) and $g(\mathbb{E}[|X|^r])\leq \mathbb{E}[g(|X|^r)]=\mathbb{E}[|X|^s].$ As a consequence, $\mathbb{E}[|X|^s]<\infty\implies\mathbb{E}[|X|^r]<\infty$ for $0\leq r\leq s.$⁵
5. The exponential (logarithm) function is convex (concave). Consequently, $\exp(\mathbb{E}[X])\leq\mathbb{E}[\exp(X)]$ and $\log(\mathbb{E}[|X|])\geq\mathbb{E}[\log(|X|)].$

---

2. Inspiration for (1.1) comes from realizing that $F(x)=\mathbb{E}[1_{\{X\leq x\}}].$↩︎

3. See Riemann–Stieltjes integral.↩︎

4. Recall that the $X$-part of $\mathbb{E}[Y| X]$ is random. However, $\mathbb{E}[Y| X=x]$ is deterministic.↩︎

5. “Finite moments of higher order imply finite moments of lower order”.↩︎