1.4 OP and oP notation

1.4.1 Deterministic versions

In computer science the O notation is used to measure the complexity of algorithms. For example, when an algorithm is O(n2), it is said that it is quadratic in time and we know that is going to take on the order of n2 operations to process an input of size n. We do not care about the specific amount of computations; rather, we focus on the big picture by looking for an upper bound for the sequence of computation times in terms of n. This upper bound disregards constants. For example, the dot product between two vectors of size n is an O(n) operation, although it takes n multiplications and n−1 sums, hence 2n−1 operations.

In mathematical analysis, O-related notation is mostly used to bound sequences that shrink to zero. The technicalities are however the same.

Definition 1.5 (Big-O) Given two strictly positive sequences an and bn,

an=O(bn):⟺lim sup

If a_n=O(b_n), then we say that a_n is big-O of b_n. To indicate that a_n is bounded, we write a_n=O(1).11

Definition 1.6 (Little-o) Given two strictly positive sequences a_n and b_n,

\begin{align*} a_n=o(b_n)\,:\!\iff \lim_{n\to\infty}\frac{a_n}{b_n}=0. \end{align*}

If a_n=o(b_n), then we say that a_n is little-o of b_n. To indicate that a_n\to0, we write a_n=o(1).

Remark. An immediate but important consequence of the big-O and little-o definitions is that

\begin{align} a_n=O(b_n)\!\iff \frac{a_n}{b_n}=O(1) \text{ and } a_n=o(b_n)\!\iff \frac{a_n}{b_n}=o(1). \tag{1.7} \end{align}

Exercise 1.11 Show the following statements by directly applying the previous definitions.

  1. n^{-2}=o(n^{-1}).
  2. \log n=O(n).
  3. n^{-1}=o((\log n)^{-1}).
  4. n^{-4/5}=o(n^{-2/3}).
  5. 3\sin(n)=O(1).
  6. n^{-2}-n^{-3}+n^{-1}=O(n^{-1}).
  7. n^{-2}-n^{-3}=o(n^{-1/2}).

The interpretation of these two definitions is simple:

  • a_n=O(b_n) means that a_n is “not larger than” b_n asymptotically. If a_n,b_n\to0, then it means that a_n “decreases as fast or faster” than b_n.
  • a_n=o(b_n) means that a_n is “smaller than” b_n asymptotically. If a_n,b_n\to0, then it means that a_n “decreases faster” than b_n.

Obviously, little-o implies big-O (take any C>0 in Definition 1.5). Playing with limits we can get a list of useful facts.

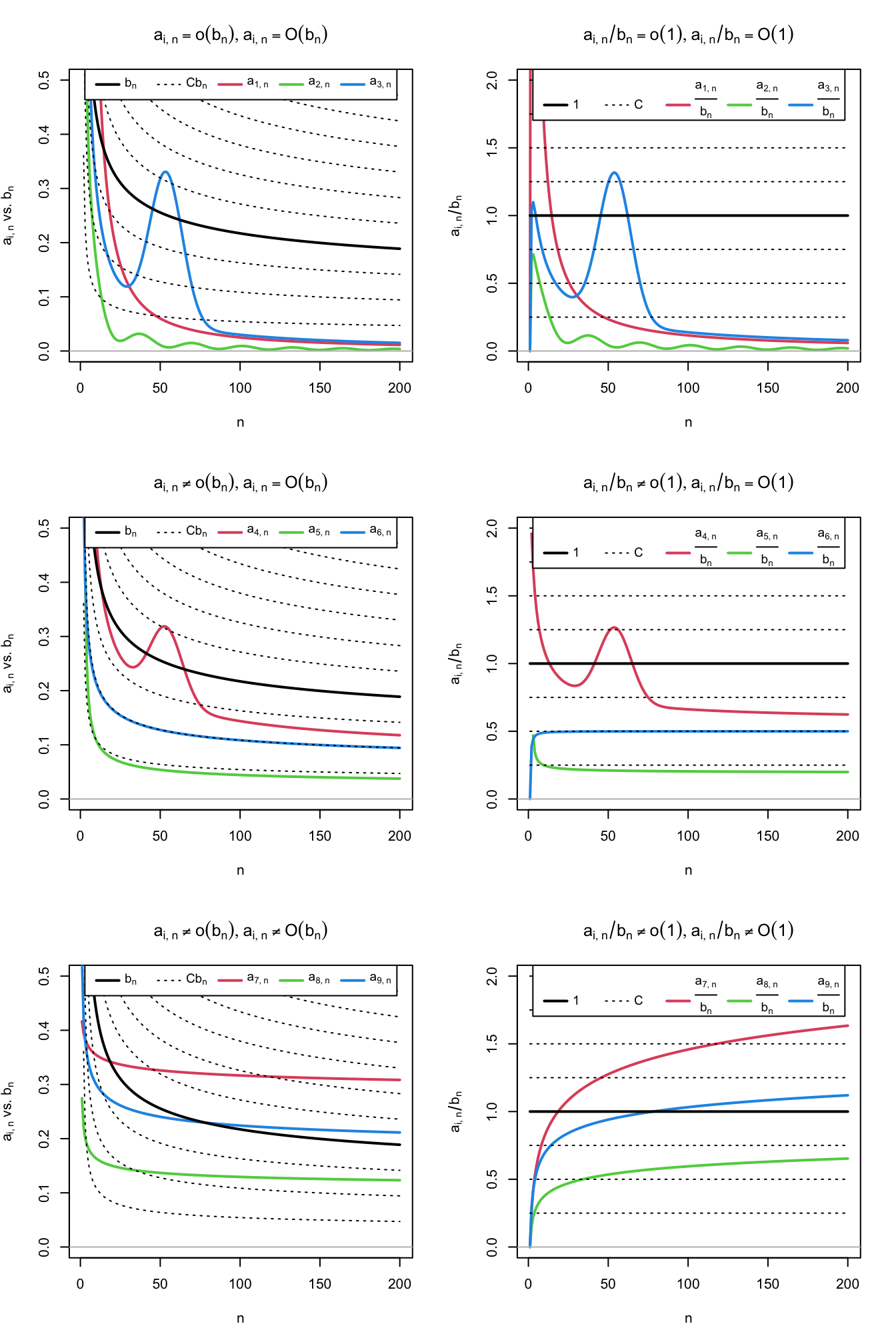
Differences and similarities between little-\(o\) and big-\(O,\) illustrated for the dominating sequence \(b_n=1/\log(n)\) (black solid curve) and sequences \(a_{i,n},\) \(j=1,\ldots,9\) (colored curves). The dashed lines represent the sequences \(Cb_n,\) for a grid of constants \(C.\) The plots on the left column compare \(a_{i,n}\) against \(b_n,\) whereas the right column plots show the equivalent view in terms of the ratios \(a_{i,n}/b_n\) (recall (1.7)). Sequences \(a_{1,n}=2 / n + 50 / n^2,\) \(a_{2,n}=(\sin(n/5) + 2) / n^{5/4},\) and \(a_{3,n}=3(1 + 5 \exp(-(n - 55.5)^2 / 200)) / n\) are \(o(b_n)\) (hence also \(O(b_n)\)). Sequences \(a_{4,n}=(2\log_{10}(n)((n + 3) / (2n)))^{-1} + a_{3,n}/2,\) \(a_{5,n}=(4\log_2(n/2))^{-1},\) and \(a_{6,n}=(\log(n^2 + n))^{-1}\) are \(O(b_n),\) but not \(o(b_n).\) Finally, sequences \(a_{7,n}=\log(5n + 3)^{-1/4}/2,\) \(a_{8,n}=(4\log(\log(10n + 2)))^{-1},\) and \(a_{9,n}=(2\log(\log(n^2 + 10n + 2)))^{-1}\) are not \(O(b_n)\) (hence neither \(o(b_n)\)).

Figure 1.2: Differences and similarities between little-o and big-O, illustrated for the dominating sequence b_n=1/\log(n) (black solid curve) and sequences a_{i,n}, j=1,\ldots,9 (colored curves). The dashed lines represent the sequences Cb_n, for a grid of constants C. The plots on the left column compare a_{i,n} against b_n, whereas the right column plots show the equivalent view in terms of the ratios a_{i,n}/b_n (recall (1.7)). Sequences a_{1,n}=2 / n + 50 / n^2, a_{2,n}=(\sin(n/5) + 2) / n^{5/4}, and a_{3,n}=3(1 + 5 \exp(-(n - 55.5)^2 / 200)) / n are o(b_n) (hence also O(b_n)). Sequences a_{4,n}=(2\log_{10}(n)((n + 3) / (2n)))^{-1} + a_{3,n}/2, a_{5,n}=(4\log_2(n/2))^{-1}, and a_{6,n}=(\log(n^2 + n))^{-1} are O(b_n), but not o(b_n). Finally, sequences a_{7,n}=\log(5n + 3)^{-1/4}/2, a_{8,n}=(4\log(\log(10n + 2)))^{-1}, and a_{9,n}=(2\log(\log(n^2 + 10n + 2)))^{-1} are not O(b_n) (hence neither o(b_n)).

Proposition 1.7 Consider two strictly positive sequences a_n,b_n\to0. The following properties hold:

  1. kO(a_n)=O(a_n), ko(a_n)=o(a_n), k\in\mathbb{R}.
  2. o(a_n)+o(b_n)=o(a_n+b_n), O(a_n)+O(b_n)=O(a_n+b_n).
  3. o(a_n)o(b_n)=o(a_nb_n), O(a_n)O(b_n)=O(a_nb_n).
  4. o(a_n)+O(b_n)=O(a_n+b_n), o(a_n)O(b_n)=o(a_nb_n).
  5. o(1)O(a_n)=o(a_n).
  6. a_n^r=o(a_n^s), for r>s\geq 0.
  7. a_nb_n=o(a_n^2+b_n^2).
  8. a_nb_n=o(a_n+b_n).
  9. (a_n+b_n)^k=O(a_n^k+b_n^k).

The last result is a consequence of a useful inequality.

Lemma 1.1 (C_p inequality) Given a,b\in\mathbb{R} and p>0,

\begin{align*} |a+b|^p\leq C_p(|a|^p+|b|^p), \quad C_p=\begin{cases} 1,&p\leq1,\\ 2^{p-1},&p>1. \end{cases} \end{align*}

Exercise 1.12 Illustrate the properties of Proposition 1.7 considering a_n=n^{-1} and b_n=n^{-1/2}.

1.4.2 Stochastic versions

The previous notation is purely deterministic. Let’s add some stochastic flavor by establishing the stochastic analogous of little-o.

Definition 1.7 (Little-o_\mathbb{P}) Given a strictly positive sequence a_n and a sequence of random variables X_n,

\begin{align*} X_n=o_\mathbb{P}(a_n)\,:\!\iff& \frac{|X_n|}{a_n}\stackrel{\mathbb{P}}{\longrightarrow}0 \\ \iff& \lim_{n\to\infty}\mathbb{P}\left[\frac{|X_n|}{a_n}>\varepsilon\right]=0,\;\forall\varepsilon>0. \end{align*}

If X_n=o_\mathbb{P}(a_n), then we say that X_n is little-o_\mathbb{P} of a_n. To indicate that X_n\stackrel{\mathbb{P}}{\longrightarrow}0, we write X_n=o_\mathbb{P}(1).

Therefore, little-o_\mathbb{P} allows us to easily quantify the speed at which a sequence of random variables converges to zero in probability.

Example 1.3 Let Y_n=o_\mathbb{P}\big(n^{-1/2}\big) and Z_n=o_\mathbb{P}(n^{-1}). Then Z_n converges faster to zero in probability than Y_n. To visualize this, recall that X_n=o_\mathbb{P}(a_n) and that limit definitions entail that

\begin{align*} \forall\varepsilon,\delta>0,\,\exists \,n_0=n_0(\varepsilon,\delta)\in\mathbb{N}:\forall n\geq n_0(\varepsilon,\delta),\, \mathbb{P}\left[|X_n|>a_n\varepsilon\right]<\delta. \end{align*}

Therefore, for fixed \varepsilon,\delta>0 and a fixed n\geq\max(n_{0,Y},n_{0,Z}), then \mathbb{P}\left[Y_n\in\big(-n^{-1/2}\varepsilon,n^{-1/2}\varepsilon\big)\right]>1-\delta and \mathbb{P}\left[Z_n\in(-n^{-1}\varepsilon,n^{-1}\varepsilon)\right]>1-\delta, but the latter interval is much shorter, hence Z_n is forced to be more tightly concentrated about 0.

Big-O_\mathbb{P} allows us to bound a sequence of random variables in probability, in the sense that we can state that the probability of being above an arbitrarily large threshold C converges to zero. As with its deterministic versions o and O, a little-o_\mathbb{P} is more restrictive than a big-O_\mathbb{P}, and the former implies the latter.

Definition 1.8 (Big-O_\mathbb{P}) Given a strictly positive sequence a_n and a sequence of random variables X_n,

\begin{align*} X_n=O_\mathbb{P}(a_n)\,:\!\iff&\forall\varepsilon>0,\,\exists\,C_\varepsilon>0,\,n_0(\varepsilon)\in\mathbb{N}:\\ &\forall n\geq n_0(\varepsilon),\, \mathbb{P}\left[\frac{|X_n|}{a_n}>C_\varepsilon\right]<\varepsilon\\ \iff& \lim_{C\to\infty}\limsup_{n\to\infty}\mathbb{P}\left[\frac{|X_n|}{a_n}>C\right]=0. \end{align*}

If X_n=O_\mathbb{P}(a_n), then we say that X_n is big-O_\mathbb{P} of a_n.

Remark. An immediate but important consequence of the big-O_\mathbb{P} and little-o_\mathbb{P} definitions is that

\begin{align} X_n=O_\mathbb{P}(a_n)\!\iff \frac{X_n}{a_n}=O_\mathbb{P}(1) \text{ and } X_n=o_\mathbb{P}(a_n)\!\iff \frac{X_n}{a_n}=o_\mathbb{P}(1). \tag{1.8} \end{align}

Example 1.4 Any sequence of random variables such that X_n=X for all n\geq 1, with X any random variable, is trivially X_n=O_\mathbb{P}(1). Indeed, it is satisfied that \lim_{C\to\infty}\limsup_{n\to\infty}\mathbb{P}\left[\frac{|X_n|}{1}>C\right]=\lim_{C\to\infty}\mathbb{P}[|X_n|>C]=0.

Example 1.5 Chebyshev inequality entails that \mathbb{P}[|X_n-\mathbb{E}[X_n]|\geq t]\leq \mathbb{V}\mathrm{ar}[X_n]/t^2, \forall t>0. Setting \varepsilon:=\mathbb{V}\mathrm{ar}[X_n]/t^2 and C_\varepsilon:=1/\sqrt{\varepsilon}, then \mathbb{P}\left[|X_n-\mathbb{E}[X_n]|\geq \sqrt{\mathbb{V}\mathrm{ar}[X_n]}C_\varepsilon\right]\leq \varepsilon. Therefore,

\begin{align} X_n-\mathbb{E}[X_n]=O_\mathbb{P}\left(\sqrt{\mathbb{V}\mathrm{ar}[X_n]}\right).\tag{1.9} \end{align}

This is a very useful result, as it gives an efficient way of deriving the big-O_\mathbb{P} form of a sequence of random variables X_n with finite variances.

An application of Example 1.5 shows that X_n=O_\mathbb{P}(n^{-1/2}) for X_n\stackrel{d}{=}\mathcal{N}(0,1/n). The nature of this statement and its relation with little-o_\mathbb{P} is visualized with Figure 1.3, which shows a particular realization X_n(\omega) of the sequence of random variables.

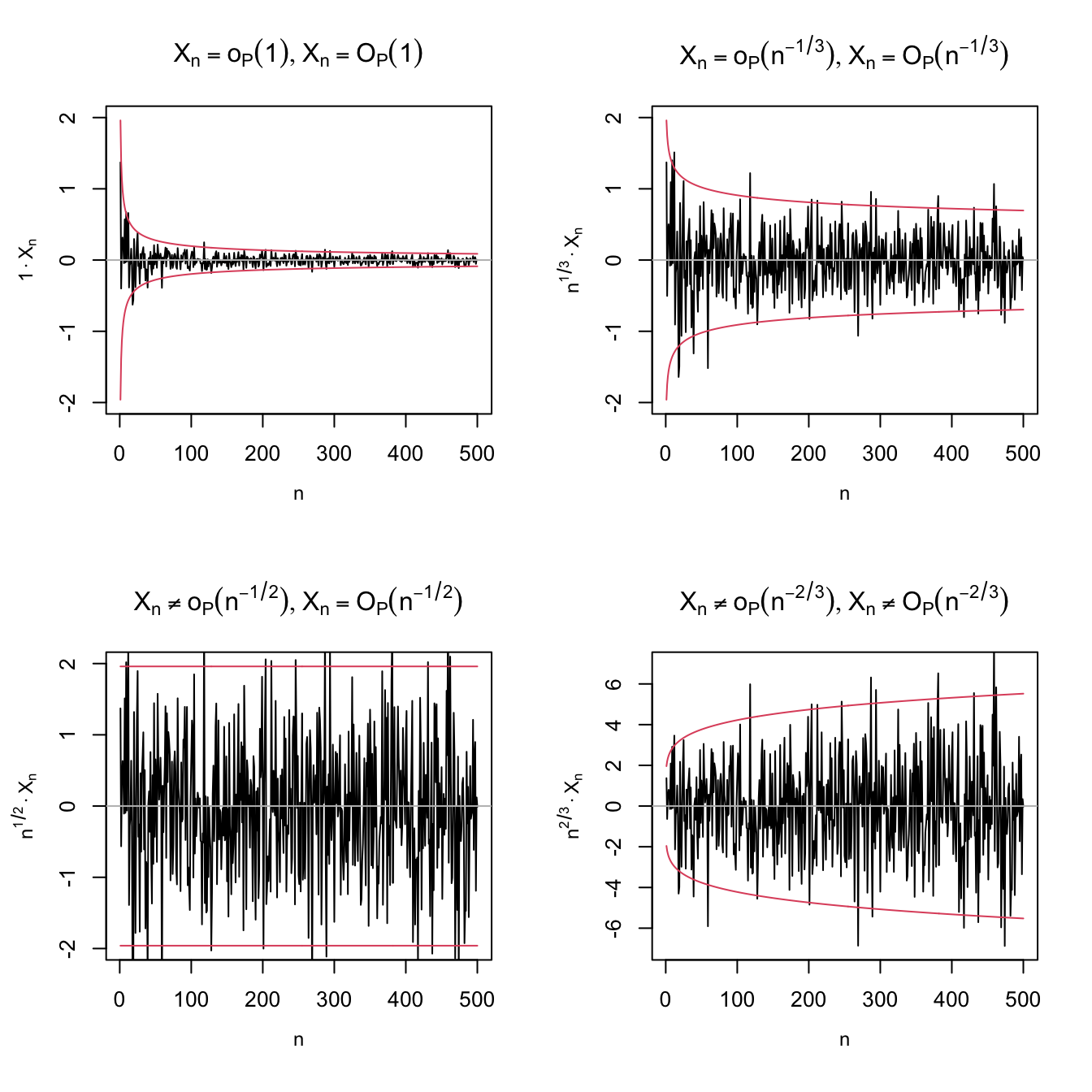
Differences and similarities between little-\(o_\mathbb{P}\) and big-\(O_\mathbb{P},\) illustrated for the sequence of random variables \(X_n\stackrel{d}{=}\mathcal{N}(0,1/n).\) Since \(X_n\stackrel{\mathbb{P}}{\longrightarrow}0,\) \(X_n=o_\mathbb{P}(1),\) as evidenced in the upper left plot. The next plots check if \(X_n=o_\mathbb{P}(a_n)\) by evaluating if \(X_n/a_n\stackrel{\mathbb{P}}{\longrightarrow}0\) (recall (1.8)), for \(a_n=n^{-1/3},n^{-1/2},n^{-2/3}.\) Clearly, \(X_n=o_\mathbb{P}(n^{-1/3})\) (\(n^{1/3}X_n\stackrel{\mathbb{P}}{\longrightarrow}0\)) but \(X_n\neq o_\mathbb{P}(n^{-1/2})\) (\(n^{1/2}X_n\stackrel{\mathbb{P}}{\longrightarrow}\mathcal{N}(0,1)\)) and \(X_n\neq o_\mathbb{P}(n^{-2/3})\) (\(n^{2/3}X_n\) diverges). In the first three cases, \(X_n=O_\mathbb{P}(a_n);\) the fourth is \(X_n\neq O_\mathbb{P}(n^{-2/3}),\) \(n^{2/3}X_n\) is not bounded in probability. The red lines represent the \(95\%\) confidence intervals \(\left(-z_{0.025}/(a_n\sqrt{n}),z_{0.025}/(a_n\sqrt{n})\right)\) of the random variable \(X_n/a_n,\) and help evaluating graphically the convergence in probability towards zero.

Figure 1.3: Differences and similarities between little-o_\mathbb{P} and big-O_\mathbb{P}, illustrated for the sequence of random variables X_n\stackrel{d}{=}\mathcal{N}(0,1/n). Since X_n\stackrel{\mathbb{P}}{\longrightarrow}0, X_n=o_\mathbb{P}(1), as evidenced in the upper left plot. The next plots check if X_n=o_\mathbb{P}(a_n) by evaluating if X_n/a_n\stackrel{\mathbb{P}}{\longrightarrow}0 (recall (1.8)), for a_n=n^{-1/3},n^{-1/2},n^{-2/3}. Clearly, X_n=o_\mathbb{P}(n^{-1/3}) (n^{1/3}X_n\stackrel{\mathbb{P}}{\longrightarrow}0) but X_n\neq o_\mathbb{P}(n^{-1/2}) (n^{1/2}X_n\stackrel{\mathbb{P}}{\longrightarrow}\mathcal{N}(0,1)) and X_n\neq o_\mathbb{P}(n^{-2/3}) (n^{2/3}X_n diverges). In the first three cases, X_n=O_\mathbb{P}(a_n); the fourth is X_n\neq O_\mathbb{P}(n^{-2/3}), n^{2/3}X_n is not bounded in probability. The red lines represent the 95\% confidence intervals \left(-z_{0.025}/(a_n\sqrt{n}),z_{0.025}/(a_n\sqrt{n})\right) of the random variable X_n/a_n, and help evaluating graphically the convergence in probability towards zero.

Exercise 1.13 As illustrated in Figure 1.3, prove that it is actually true that:

  1. X_n\stackrel{\mathbb{P}}{\longrightarrow}0.
  2. n^{1/3}X_n\stackrel{\mathbb{P}}{\longrightarrow}0.
  3. n^{1/2}X_n\stackrel{\mathbb{P}}{\longrightarrow}\mathcal{N}(0,1).

Exercise 1.14 Prove that if X_n\stackrel{d}{\longrightarrow}X, then X_n=O_\mathbb{P}(1). Hint: use the double-limit definition and note that X=O_\mathbb{P}(1).

Example 1.6 (Example 1.18 in DasGupta (2008)) Suppose that a_n(X_n-c_n)\stackrel{d}{\longrightarrow}X for deterministic sequences a_n and c_n such that c_n\to c. Then, if a_n\to\infty, X_n-c=o_\mathbb{P}(1). The argument is simple:

\begin{align*} X_n-c&=X_n-c_n+c_n-c\\ &=\frac{1}{a_n}a_n(X_n-c_n)+o(1)\\ &=\frac{1}{a_n}O_\mathbb{P}(1)+o(1). \end{align*}

Exercise 1.15 Using the previous example, derive the weak law of large numbers as a consequence of the CLT, both for id and non-id independent random variables.

Proposition 1.8 Consider two strictly positive sequences a_n,b_n\to 0. The following properties hold:

  1. o_\mathbb{P}(a_n)=O_\mathbb{P}(a_n) (little-o_\mathbb{P} implies big-O_\mathbb{P}).
  2. o(1)=o_\mathbb{P}(1), O(1)=O_\mathbb{P}(1) (deterministic implies probabilistic).
  3. kO_\mathbb{P}(a_n)=O_\mathbb{P}(a_n), ko_\mathbb{P}(a_n)=o_\mathbb{P}(a_n), k\in\mathbb{R}.
  4. o_\mathbb{P}(a_n)+o_\mathbb{P}(b_n)=o_\mathbb{P}(a_n+b_n), O_\mathbb{P}(a_n)+O_\mathbb{P}(b_n)=O_\mathbb{P}(a_n+b_n).
  5. o_\mathbb{P}(a_n)o_\mathbb{P}(b_n)=o_\mathbb{P}(a_nb_n), O_\mathbb{P}(a_n)O_\mathbb{P}(b_n)=O_\mathbb{P}(a_nb_n).
  6. o_\mathbb{P}(a_n)+O_\mathbb{P}(b_n)=O_\mathbb{P}(a_n+b_n), o_\mathbb{P}(a_n)O_\mathbb{P}(b_n)=o_\mathbb{P}(a_nb_n).
  7. o_\mathbb{P}(1)O_\mathbb{P}(a_n)=o_\mathbb{P}(a_n).
  8. (1+o_\mathbb{P}(1))^{-1}=O_\mathbb{P}(1).

Example 1.7 Example 1.5 allows us to obtain the O_\mathbb{P}-part of a sequence of random variables X_n with finite variances using (1.9). As a result of ii and iv in Proposition 1.8, we can also further simplify the coarse-grained description of X_n as

\begin{align*} X_n&=O(\mathbb{E}[X_n])+O_\mathbb{P}\left(\sqrt{\mathbb{V}\mathrm{ar}[X_n]}\right)\\ &=O_\mathbb{P}\left(\mathbb{E}[X_n]+\sqrt{\mathbb{V}\mathrm{ar}[X_n]}\right). \end{align*}

Exercise 1.16 Consider the following sequences of random variables:

  1. X_n\stackrel{d}{=}\Gamma(n+1,2n)-2.
  2. X_n\stackrel{d}{=}\mathrm{B}(n,1/n)-1.
  3. X_n\stackrel{d}{=}\mathcal{LN}(0,n^{-1})-\exp((2n)^{-1}). Hint: Use that e^x=1+x+o(x) for x\to0.

For each X_n, obtain, if possible, two different positive sequences a_n,b_n\to0 such that:

  1. X_n=o_\mathbb{P}(a_n).
  2. X_n\neq o_\mathbb{P}(b_n), X_n=O_\mathbb{P}(b_n).

Use (1.9) and check your results by performing an analogous analysis to that in Figure 1.3.

References

DasGupta, A. 2008. Asymptotic Theory of Statistics and Probability. Springer Texts in Statistics. New York: Springer. https://doi.org/10.1007/978-0-387-75971-5.

  1. For a deterministic sequence a_n, \limsup_{n\to\infty}a_n:=\lim_{n\to\infty}\left(\sup_{k\geq n}a_k\right) is the largest limit of the subsequences of a_n. It can be defined even if \lim_{n\to\infty}a_n does not exist (e.g., in trigonometric functions). If \lim_{n\to\infty}a_n exists, as in most of the common usages of the big-O notation, then \limsup_{n\to\infty}a_n=\lim_{n\to\infty}a_n.↩︎