2.4 Bandwidth selection

As we saw in the previous sections, the kde critically depends on the bandwidth employed. The purpose of this section is to introduce objective and automatic bandwidth selectors that attempt to minimize the estimation error of the target density \(f.\)

The first step is to define a global, rather than local, error criterion. The Integrated Squared Error (ISE),

\[\begin{align*} \mathrm{ISE}[\hat{f}(\cdot;h)]:=\int (\hat{f}(x;h)-f(x))^2\,\mathrm{d}x, \end{align*}\]

is the squared distance between the kde and the target density. The ISE is a random quantity, since it depends directly on the sample \(X_1,\ldots,X_n.\) As a consequence, looking for an optimal-ISE bandwidth is a hard task, since the optimality is dependent on the sample itself and not only on the population and \(n.\) To avoid this problem, it is usual to compute the Mean Integrated Squared Error (MISE):

\[\begin{align*} \mathrm{MISE}[\hat{f}(\cdot;h)]:=&\,\mathbb{E}\left[\mathrm{ISE}[\hat{f}(\cdot;h)]\right]\\ =&\,\mathbb{E}\left[\int (\hat{f}(x;h)-f(x))^2\,\mathrm{d}x\right]\\ =&\,\int \mathbb{E}\left[(\hat{f}(x;h)-f(x))^2\right]\,\mathrm{d}x\\ =&\,\int \mathrm{MSE}[\hat{f}(x;h)]\,\mathrm{d}x. \end{align*}\]

The MISE is convenient due to its mathematical tractability and its natural relation to the MSE. There are, however, other error criteria that present attractive properties, such as the Mean Integrated Absolute Error (MIAE):

\[\begin{align*} \mathrm{MIAE}[\hat{f}(\cdot;h)]:=&\,\mathbb{E}\left[\int |\hat{f}(x;h)-f(x)|\,\mathrm{d}x\right]\\ =&\,\int \mathbb{E}\left[|\hat{f}(x;h)-f(x)|\right]\,\mathrm{d}x. \end{align*}\]

The MIAE, unlike the MISE, has the appeal of being invariant with respect to monotone transformations of the density. For example, if \(g(x)=f(t^{-1}(x))(t^{-1})'(x)\) is the density of \(Y=t(X)\) and \(X\sim f,\) then the change of variables³⁷ \(y=t(x)\) gives

\[\begin{align*} \int |\hat{f}(x;h)-f(x)|\,\mathrm{d}x&=\int |\hat{f}(t^{-1}(y);h)-f(t^{-1}(y))|(t^{-1})'(y)\,\mathrm{d}y\\ &=\int |\hat g(y;h)-g(y)|\,\mathrm{d}y. \end{align*}\]

Despite this attractive invariance property, the analysis of MIAE is substantially more complicated than the MISE. We refer to Devroye and Györfi (1985) for a comprehensive treatment of absolute value metrics for kde.

Once the MISE is set as the error criterion to be minimized, our aim is to find

\[\begin{align} h_\mathrm{MISE}:=\arg\min_{h>0}\mathrm{MISE}[\hat{f}(\cdot;h)]. \tag{2.22} \end{align}\]

For that purpose, we need an explicit expression of the MISE which we can attempt to minimize. The following asymptotic expansion for the MISE solves this issue.

Corollary 2.2 Under A1–A3,

\[\begin{align} \mathrm{MISE}[\hat{f}(\cdot;h)]=&\,\frac{1}{4}\mu^2_2(K)R(f'')h^4+\frac{R(K)}{nh}\nonumber\\ &+o(h^4+(nh)^{-1}).\tag{2.23} \end{align}\]

Therefore, \(\mathrm{MISE}[\hat{f}(\cdot;h)]\to0\) when \(n\to\infty.\)

Exercise 2.13 Prove Corollary 2.2 by integrating the MSE of \(\hat{f}(x;h).\)

The dominating part of the MISE is denoted by AMISE, which stands for Asymptotic MISE:

\[\begin{align*} \mathrm{AMISE}[\hat{f}(\cdot;h)]=\frac{1}{4}\mu^2_2(K)R(f'')h^4+\frac{R(K)}{nh}. \end{align*}\]

The closed-form expression of the AMISE allows obtaining a bandwidth that minimizes this error.

Corollary 2.3 The bandwidth that minimizes the AMISE is

\[\begin{align*} h_\mathrm{AMISE}=\left[\frac{R(K)}{\mu_2^2(K)R(f'')n}\right]^{1/5}. \end{align*}\]

The optimal AMISE is:

\[\begin{align} \inf_{h>0}\mathrm{AMISE}[\hat{f}(\cdot;h)]=\frac{5}{4}(\mu_2^2(K)R(K)^4)^{1/5}R(f'')^{1/5}n^{-4/5}.\tag{2.24} \end{align}\]

Exercise 2.14 Prove Corollary 2.3 by solving \(\frac{\mathrm{d}}{\mathrm{d}h}\mathrm{AMISE}[\hat{f}(\cdot;h)]=0.\)

The AMISE-optimal order deserves some further inspection. It can be seen in Section 3.2 in Scott (2015) that the AMISE-optimal order for the histogram of Section 2.1.1 (not the moving histogram) is \(\left(3/4\right)^{2/3}R(f')^{1/3}n^{-2/3}.\) Two aspects are interesting when comparing this result with (2.24):

• First, the MISE of the histogram is asymptotically larger than the MISE of the kde.³⁸ This is a quantification of the quite apparent visual improvement of the kde over the histogram.
• Second, \(R(f')\) appears instead of \(R(f''),\) evidencing that the histogram is affected by how fast \(f\) varies and not only by the curvature of the target density \(f.\)

Unfortunately, the AMISE bandwidth depends on \(R(f'')=\int(f''(x))^2\,\mathrm{d}x,\) which measures the curvature of the density. As a consequence, it can not be readily applied in practice, as \(R(f'')\) is unknown! In the next subsection we will see how to plug-in estimates for \(R(f'').\)

2.4.1 Plug-in rules

A simple solution to estimate \(R(f'')\) is to assume that \(f\) is the density of a \(\mathcal{N}(\mu,\sigma^2)\) and then plug-in the form of the curvature for such density,³⁹

\[\begin{align*} R(\phi''_\sigma(\cdot-\mu))=\frac{3}{8\pi^{1/2}\sigma^5}. \end{align*}\]

While doing so, we approximate the curvature of an arbitrary density by means of the curvature of a normal and we have that

\[\begin{align*} h_\mathrm{AMISE}=\left[\frac{8\pi^{1/2}R(K)}{3\mu_2^2(K)n}\right]^{1/5}\sigma. \end{align*}\]

Interestingly, the bandwidth is directly proportional to the standard deviation of the target density. Replacing \(\sigma\) by an estimate yields the normal scale bandwidth selector, which we denote \(\hat{h}_\mathrm{NS}\) to emphasize its randomness:

\[\begin{align*} \hat{h}_\mathrm{NS}=\left[\frac{8\pi^{1/2}R(K)}{3\mu_2^2(K)n}\right]^{1/5}\hat\sigma. \end{align*}\]

The estimate \(\hat\sigma\) can be chosen as the standard deviation \(s,\) or, in order to avoid the effects of potential outliers, as the standardized interquantile range

\[\begin{align*} \hat \sigma_{\mathrm{IQR}}:=\frac{X_{([0.75n])}-X_{([0.25n])}}{\Phi^{-1}(0.75)-\Phi^{-1}(0.25)} \end{align*}\]

or as

\[\begin{align} \hat\sigma=\min(s,\hat \sigma_{\mathrm{IQR}}). \tag{2.25} \end{align}\]

When combined with a normal kernel, for which \(\mu_2(K)=1\) and \(R(K)=\frac{1}{2\sqrt{\pi}},\) this particularization of \(\hat{h}_{\mathrm{NS}}\) featuring (2.25) gives the famous rule-of-thumb for bandwidth selection:

\[\begin{align*} \hat{h}_\mathrm{RT}=\left(\frac{4}{3}\right)^{1/5}n^{-1/5}\hat\sigma\approx1.06n^{-1/5}\hat\sigma. \end{align*}\]

\(\hat{h}_{\mathrm{RT}}\) is implemented in R through the function bw.nrd.⁴⁰

# Data
set.seed(667478)
n <- 100
x <- rnorm(n)

# Rule-of-thumb
bw.nrd(x = x)
## [1] 0.4040319
# bwd.nrd employs 1.34 as an approximation for diff(qnorm(c(0.25, 0.75)))

# Same as
iqr <- diff(quantile(x, c(0.25, 0.75))) / diff(qnorm(c(0.25, 0.75)))
1.06 * n^(-1/5) * min(sd(x), iqr)
## [1] 0.4040319

The previous selector is an example of a zero-stage plug-in selector, a terminology inspired by the fact that the scalar \(R(f'')\) was estimated by plugging a parametric assumption directly, without attempting a nonparametric estimation first. Another possibility could have been to estimate \(R(f'')\) nonparametrically and then to plug-in the estimate into \(h_\mathrm{AMISE}.\) Let’s explore this possibility in more detail next.

First, note the useful equality

\[\begin{align*} \int f^{(s)}(x)^2\,\mathrm{d}x=(-1)^s\int f^{(2s)}(x)f(x)\,\mathrm{d}x. \end{align*}\]

This equality follows by an iterative application of integration by parts. For example, for \(s=2,\) take \(u=f''(x)\) and \(\,\mathrm{d}v=f''(x)\,\mathrm{d}x.\) It gives

\[\begin{align*} \int f''(x)^2\,\mathrm{d}x&=[f''(x)f'(x)]_{-\infty}^{+\infty}-\int f'(x)f'''(x)\,\mathrm{d}x\\ &=-\int f'(x)f'''(x)\,\mathrm{d}x \end{align*}\]

under the assumption that the derivatives vanish at infinity. Applying again integration by parts with \(u=f'''(x)\) and \(\,\mathrm{d}v=f'(x)\,\mathrm{d}x\) gives the result. This simple derivation has an important consequence: for estimating the functionals \(R(f^{(s)})\) it suffices to estimate the functionals

\[\begin{align} \psi_r:=\int f^{(r)}(x)f(x)\,\mathrm{d}x=\mathbb{E}[f^{(r)}(X)] \tag{2.26} \end{align}\]

for \(r=2s.\) In particular, \(R(f'')=\psi_4.\)

Thanks to the expression (2.26), a possible way to estimate \(\psi_r\) nonparametrically is

\[\begin{align} \hat\psi_r(g)&=\frac{1}{n}\sum_{i=1}^n\hat{f}^{(r)}(X_i;g)\nonumber\\ &=\frac{1}{n^2}\sum_{i=1}^n\sum_{j=1}^nL_g^{(r)}(X_i-X_j),\tag{2.27} \end{align}\]

where \(\hat{f}^{(r)}(\cdot;g)\) is the \(r\)-th derivative of a kde with bandwidth \(g\) and kernel \(L,\) i.e.,

\[\begin{align*} \hat{f}^{(r)}(x;g)=\frac{1}{ng^{r+1}}\sum_{i=1}^nL^{(r)}\left(\frac{x-X_i}{g}\right). \end{align*}\]

Note that \(g\) and \(L\) can be different from \(h\) and \(K,\) respectively. It turns out that estimating \(\psi_r\) involves the adequate selection of a bandwidth \(g.\) The agenda is analogous to the one for \(h_\mathrm{AMISE},\) but now taking into account that both \(\hat\psi_r(g)\) and \(\psi_r\) are scalar quantities:

1. Under certain regularity assumptions,⁴¹ the asymptotic bias and variance of \(\hat\psi_r(g)\) are obtained. With them, we can compute the asymptotic expansion of the MSE⁴² and obtain the Asymptotic Mean Squared Error AMSE:

   \[\begin{align*} \mathrm{AMSE}[\hat \psi_r(g)]=&\,\left\{\frac{L^{(r)}(0)}{ng^{r+1}}+\frac{\mu_2(L)\psi_{r+2}g^2}{4}\right\}+\frac{2R(L^{(r)})\psi_0}{n^2g^{2r+1}}\\ &+\frac{4}{n}\left\{\int f^{(r)}(x)^2f(x)\,\mathrm{d}x-\psi_r^2\right\}. \end{align*}\]

   Note: \(k\) is the highest integer such that \(\mu_k(L)>0.\) In these notes we have restricted the exposition to the case \(k=2\) for the kernels \(K,\) but there are theoretical gains if one allows high-order kernels \(L\) with vanishing even moments larger than \(2\) for estimating \(\psi_r.\)

2. Obtain the AMSE-optimal bandwidth:

   \[\begin{align*} g_\mathrm{AMSE}=\left[-\frac{k!L^{(r)}(0)}{\mu_k(L)\psi_{r+k}n}\right]^{1/(r+k+1)} \end{align*}\]

   The order of the optimal AMSE is

   \[\begin{align*}\inf_{g>0}\mathrm{AMSE}[\hat \psi_r(g)]=\begin{cases} O(n^{-(2k+1)/(r+k+1)}),&k<r,\\ O(n^{-1}),&k\geq r, \end{cases}\end{align*}\]

   which shows that a parametric-like rate of convergence can be achieved with high-order kernels. If we consider \(L=K\) and \(k=2,\) then

   \[\begin{align*} g_\mathrm{AMSE}=\left[-\frac{2K^{(r)}(0)}{\mu_2(K)\psi_{r+2}n}\right]^{1/(r+3)}. \end{align*}\]

The result above has a major problem: it depends on \(\psi_{r+2}\)! Thus, if we want to estimate \(R(f'')=\psi_4\) by \(\hat\psi_4(g_\mathrm{AMSE})\) we will need to estimate \(\psi_6.\) But \(\hat\psi_6(g_\mathrm{AMSE})\) will depend on \(\psi_8,\) and so on! The solution to this convoluted problem is to stop estimating the functional \(\psi_r\) after a given number \(\ell\) of stages, hence the terminology \(\ell\)-stage plug-in selector. At the \(\ell\)-th stage, the functional \(\psi_{2\ell+4}\) inside the AMSE-optimal bandwidth for estimating \(\psi_{2\ell+2}\;\) nonparametrically⁴³ is computed assuming that the density is a \(\mathcal{N}(\mu,\sigma^2),\)⁴⁴ for which

\[\begin{align*} \psi_r=\frac{(-1)^{r/2}r!}{(2\sigma)^{r+1}(r/2)!\sqrt{\pi}},\quad \text{for }r\text{ even.} \end{align*}\]

Typically, two stages are considered a good trade-off between bias (mitigated when \(\ell\) increases) and variance (increases with \(\ell\)) of the plug-in selector. This is the method proposed by Sheather and Jones (1991), where they consider \(L=K\) and \(k=2,\) yielding what we call the Direct Plug-In (DPI). The algorithm is:

1. Estimate \(\psi_8\) using \(\hat\psi_8^\mathrm{NS}:=\frac{105}{32\sqrt{\pi}\hat\sigma^9},\) where \(\hat\sigma\) is given in (2.25).

2. Estimate \(\psi_6\) using \(\hat\psi_6(g_1)\) from (2.27), where

   \[\begin{align*} g_1:=\left[-\frac{2K^{(6)}(0)}{\mu_2(K)\hat\psi^\mathrm{NS}_{8}n}\right]^{1/9}. \end{align*}\]

3. Estimate \(\psi_4\) using \(\hat\psi_4(g_2)\) from (2.27), where

   \[\begin{align*} g_2:=\left[-\frac{2K^{(4)}(0)}{\mu_2(K)\hat\psi_6(g_1)n}\right]^{1/7}. \end{align*}\]

4. The selected bandwidth is

   \[\begin{align*} \hat{h}_{\mathrm{DPI}}:=\left[\frac{R(K)}{\mu_2^2(K)\hat\psi_4(g_2)n}\right]^{1/5}. \end{align*}\]

Remark. The derivatives \(K^{(r)}\) for the normal kernel can be obtained using the (probabilists’) Hermite polynomials: \(\phi^{(r)}(x)=\phi(x)H_r(x).\) For \(r=0,\ldots,6,\) these are: \(H_0(x)=1,\) \(H_1(x)=x,\) \(H_2(x)=x^2-1,\) \(H_3(x)=x^3-3x,\) \(H_4(x)=x^4-6x^2+3,\) \(H_5(x)=x^5-10x^3+15x,\) and \(H_6(x)=x^6-15x^4+45x^2-15.\) Hermite polynomials satisfy the recurrence relation \(H_{\ell+1}(x)=xH_\ell(x)-\ell H_{\ell-1}(x)\) for \(\ell\geq1.\)

\(\hat{h}_{\mathrm{DPI}}\) is implemented in R through the function bw.SJ (use method = "dpi"). An alternative and faster implementation is ks::hpi, which also accounts for more flexibility and has a somehow more complete documentation.

# Data
set.seed(672641)
x <- rnorm(100)

# DPI selector
bw.SJ(x = x, method = "dpi")
## [1] 0.5006905

# Similar to
ks::hpi(x) # Default is two-stage
## [1] 0.4999456

Exercise 2.15 Apply and inspect the kde of airquality$Ozone using the DPI selector (both bw.SJ and ks::hpi). What can you conclude from the estimate?

2.4.2 Cross-validation

We now turn our attention to a different philosophy of bandwidth estimation. Instead of trying to minimize the AMISE by plugging estimates for the unknown curvature term, we directly attempt to minimize the MISE. The idea is to use the sample twice: one for computing the kde and other for evaluating its performance on estimating \(f.\) To avoid the clear dependence on the sample, we do this evaluation in a cross-validatory way: the data used for computing the kde is not used for its evaluation.

We begin by expanding the square in the MISE expression:

\[\begin{align*} \mathrm{MISE}[\hat{f}(\cdot;h)]=&\,\mathbb{E}\left[\int (\hat{f}(x;h)-f(x))^2\,\mathrm{d}x\right]\\ =&\,\mathbb{E}\left[\int \hat{f}(x;h)^2\,\mathrm{d}x\right]-2\mathbb{E}\left[\int \hat{f}(x;h)f(x)\,\mathrm{d}x\right]\\ &+\int f(x)^2\,\mathrm{d}x. \end{align*}\]

Since the last term does not depend on \(h,\) minimizing \(\mathrm{MISE}[\hat{f}(\cdot;h)]\) is equivalent to minimizing

\[\begin{align} \mathbb{E}\left[\int \hat{f}(x;h)^2\,\mathrm{d}x\right]-2\mathbb{E}\left[\int \hat{f}(x;h)f(x)\,\mathrm{d}x\right].\tag{2.28} \end{align}\]

This quantity is unknown, but it can be estimated unbiasedly by

\[\begin{align} \mathrm{LSCV}(h):=\int\hat{f}(x;h)^2\,\mathrm{d}x-2n^{-1}\sum_{i=1}^n\hat{f}_{-i}(X_i;h),\tag{2.29} \end{align}\]

where \(\hat{f}_{-i}(\cdot;h)\) is the leave-one-out kde and is based on the sample with the \(X_i\) removed:

\[\begin{align*} \hat{f}_{-i}(x;h)=\frac{1}{n-1}\sum_{\substack{j=1\\j\neq i}}^n K_h(x-X_j). \end{align*}\]

Exercise 2.16 Prove that (2.29) is indeed an unbiased estimator of (2.28).

Exercise 2.17 (Exercise 3.3 in Wand and Jones (1995)) Prove that \(\mathbb{E}[\mathrm{LSCV}(h)]=\mathrm{MISE}[\hat{f}(\cdot;h)]-R(f).\)

The motivation for (2.29) is the following. The first term is unbiased by design.⁴⁵ The second arises from approximating \(\int \hat{f}(x;h)f(x)\,\mathrm{d}x\) by Monte Carlo from the sample \(X_1,\ldots,X_n\sim f;\) in other words, by replacing \(f(x)\,\mathrm{d}x=\,\mathrm{d}F(x)\) with \(\mathrm{d}F_n(x).\) This gives

\[\begin{align*} \int \hat{f}(x;h)f(x)\,\mathrm{d}x\approx\frac{1}{n}\sum_{i=1}^n \hat{f}(X_i;h) \end{align*}\]

and, in order to mitigate the dependence of the sample, we replace \(\hat{f}(X_i;h)\) with \(\hat{f}_{-i}(X_i;h)\) above. In that way, we use the sample for estimating the integral involving \(\hat{f}(\cdot;h),\) but for each \(X_i\) we compute the kde on the remaining points.

The Least Squares Cross-Validation (LSCV) selector, also denoted Unbiased Cross-Validation (UCV) selector, is defined as

\[\begin{align*} \hat{h}_\mathrm{LSCV}:=\arg\min_{h>0}\mathrm{LSCV}(h). \end{align*}\]

Numerical optimization is required for obtaining \(\hat{h}_\mathrm{LSCV},\) contrary to the previous plug-in selectors, and there is little control on the shape of the objective function. This will also be the case for the subsequent bandwidth selectors. The following remark warns about the dangers of numerical optimization in this context.

Remark. Numerical optimization of the LSCV function can be challenging. In practice, several local minima are possible, and the roughness of the objective function can vary notably depending on \(n\) and \(f.\) As a consequence, optimization routines may get trapped in spurious solutions. To be on the safe side, it is always advisable to check (when possible) the solution by plotting \(\mathrm{LSCV}(h)\) for a range of \(h,\) or to perform a search in a bandwidth grid: \(\hat{h}_\mathrm{LSCV}\approx\arg\min_{h_1,\ldots,h_G}\mathrm{LSCV}(h).\)

\(\hat{h}_{\mathrm{LSCV}}\) is implemented in R through the function bw.ucv. This function uses R’s optimize, which is quite sensitive to the selection of the search interval.⁴⁶ Therefore, some care is needed; that is why the bw.ucv.mod function is presented below.

# Data
set.seed(123456)
x <- rnorm(100)

# UCV gives a warning
bw.ucv(x = x)
## [1] 0.4499177

# Extend search interval
bw.ucv(x = x, lower = 0.01, upper = 1)
## [1] 0.5482419

# bw.ucv.mod replaces the optimization routine of bw.ucv with an exhaustive
# search on "h_grid" (chosen adaptatively from the sample) and optionally
# plots the LSCV curve with "plot_cv"
bw.ucv.mod <- function(x, nb = 1000L,
                       h_grid = 10^seq(-3, log10(1.2 * sd(x) *
                                                   length(x)^(-1/5)), l = 200),
                       plot_cv = FALSE) {
  if ((n <- length(x)) < 2L)
    stop("need at least 2 data points")
  n <- as.integer(n)
  if (is.na(n))
    stop("invalid length(x)")
  if (!is.numeric(x))
    stop("invalid 'x'")
  nb <- as.integer(nb)
  if (is.na(nb) || nb <= 0L)
    stop("invalid 'nb'")
  storage.mode(x) <- "double"
  hmax <- 1.144 * sqrt(var(x)) * n^(-1/5)
  Z <- .Call(stats:::C_bw_den, nb, x)
  d <- Z[[1L]]
  cnt <- Z[[2L]]
  fucv <- function(h) .Call(stats:::C_bw_ucv, n, d, cnt, h)
  ## Original
  # h <- optimize(fucv, c(lower, upper), tol = tol)$minimum
  # if (h < lower + tol | h > upper - tol)
  #   warning("minimum occurred at one end of the range")
  ## Modification
  obj <- sapply(h_grid, function(h) fucv(h))
  h <- h_grid[which.min(obj)]
  if (h %in% range(h_grid)) 
    warning("minimum occurred at one end of h_grid")
  if (plot_cv) {
    plot(h_grid, obj, type = "o")
    rug(h_grid)
    abline(v = h, col = 2, lwd = 2)
  }
  h
}

# Compute the bandwidth and plot the LSCV curve
bw.ucv.mod(x = x, plot_cv = TRUE, h_grid = 10^seq(-1.25, 0.5, l = 200))
## [1] 0.5431561

# We can compare with the default bw.ucv output
abline(v = bw.ucv(x = x), col = 3)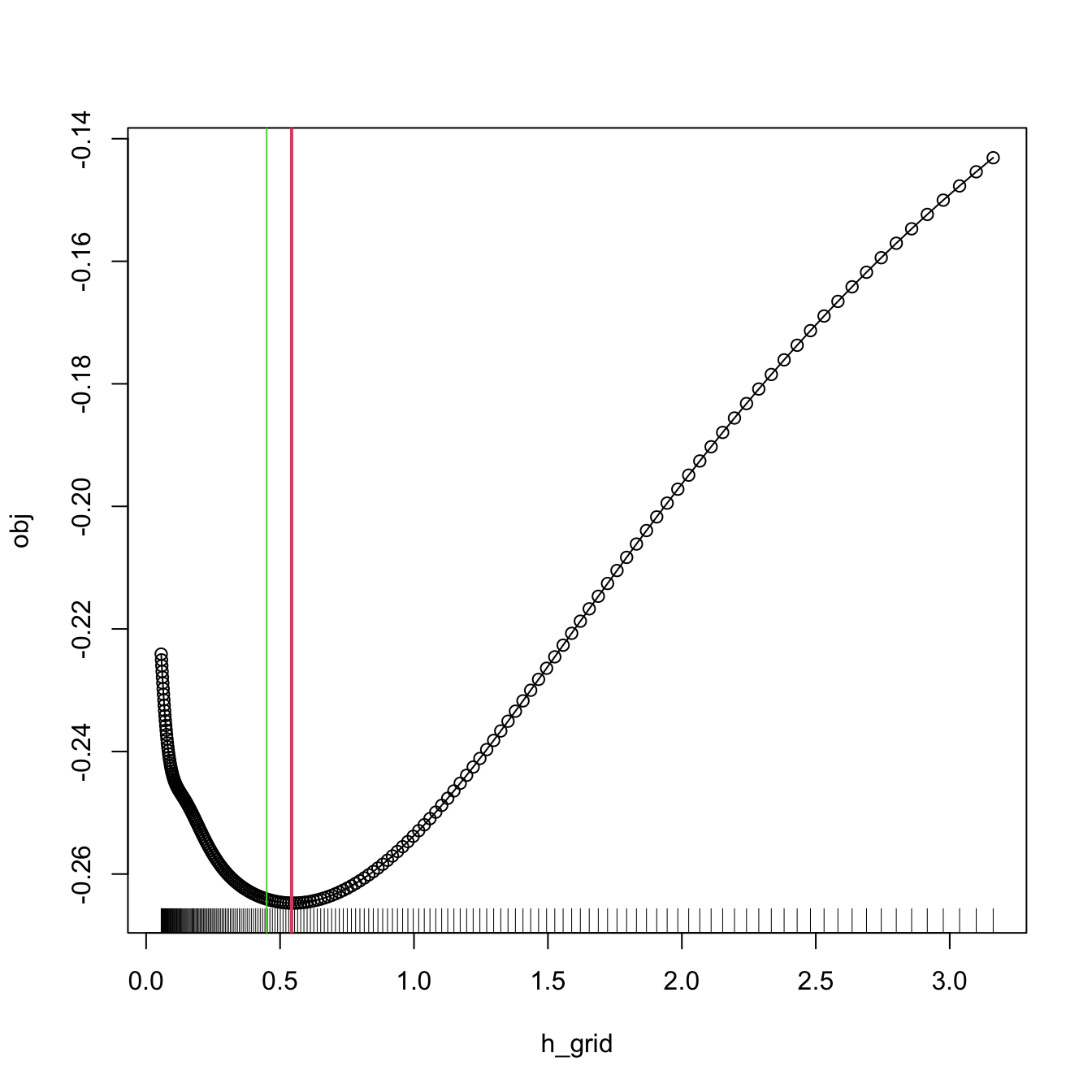

Figure 2.9: LSCV curve evaluated for a grid of bandwidths, with a clear global minimum corresponding to \(\hat{h}_\mathrm{LSCV}.\)

The next cross-validation selector is based on Biased Cross-Validation (BCV). The BCV selector presents a hybrid strategy that combines plug-in and cross-validation ideas. It starts by considering the AMISE expression in (2.23)

\[\begin{align*} \mathrm{AMISE}[\hat{f}(\cdot;h)]=\frac{1}{4}\mu^2_2(K)R(f'')h^4+\frac{R(K)}{nh} \end{align*}\]

and then plugs-in an estimate for \(R(f'')\) based on a modification of \(R(\hat{f}{}''(\cdot;h)).\) The modification is

\[\begin{align} \widetilde{R(f'')}:=&\,R(\hat{f}{}''(\cdot;h))-\frac{R(K'')}{nh^5}\nonumber\\ =&\,\frac{1}{n^2}\sum_{i=1}^n\sum_{\substack{j=1\\j\neq i}}^n(K_h''*K_h'')(X_i-X_j)\tag{2.30}, \end{align}\]

a leave-out-diagonals estimate of \(R(f'').\) It is designed to reduce the bias of \(R(\hat{f}{}''(\cdot;h)),\) since \(\mathbb{E}\big[R(\hat{f}{}''(\cdot;h))\big]=R(f'')+\frac{R(K'')}{nh^5}+O(h^2)\) (Scott and Terrell 1987). Plugging (2.30) into the AMISE expression yields the BCV objective function and the BCV bandwidth selector:

\[\begin{align*} \mathrm{BCV}(h)&:=\frac{1}{4}\mu^2_2(K)\widetilde{R(f'')}h^4+\frac{R(K)}{nh},\\ \hat{h}_\mathrm{BCV}&:=\arg\mathrm{locmin}_{h>0}\mathrm{BCV}(h), \end{align*}\]

where \(\arg\mathrm{locmin}_{h>0}\mathrm{BCV}(h)\) stands for the smallest local minimizer of \(\mathrm{BCV}(h).\) The consideration of the local minimum is because, by design, \(\mathrm{BCV}(h)\to0\) as \(h\to\infty\) for fixed \(n\): \(\widetilde{R(f'')}\to0,\) at a faster rate than \(O(h^{-4}).\) Therefore, when minimizing \(\mathrm{BCV}(h),\) some care is required, as one is actually interested in obtaining the smallest local minimizer. Consequently, bandwidth grids with an upper extreme that is too large⁴⁷ are to be avoided, as these will miss the local minimum in favor of the global one at \(h\to\infty.\)

The most appealing property of \(\hat{h}_\mathrm{BCV}\) is that it has a considerably smaller variance than \(\hat{h}_\mathrm{LSCV}.\) This reduction in variance comes at the price of an increased bias, which tends to make \(\hat{h}_\mathrm{BCV}\) larger than \(h_\mathrm{MISE}.\)

\(\hat{h}_{\mathrm{BCV}}\) is implemented in R through the function bw.bcv. Again, bw.bcv uses R’s optimize so the bw.bcv.mod function is presented to have better guarantees on finding the first local minimum. Quite some care is needed with the range of bandwidth grid, though, to avoid the global minimum for large bandwidths.

# Data
set.seed(123456)
x <- rnorm(100)

# BCV gives a warning
bw.bcv(x = x)
## [1] 0.4500924

# Extend search interval
args(bw.bcv)
## function (x, nb = 1000L, lower = 0.1 * hmax, upper = hmax, tol = 0.1 * 
##     lower) 
## NULL
bw.bcv(x = x, lower = 0.01, upper = 1)
## [1] 0.5070129

# bw.bcv.mod replaces the optimization routine of bw.bcv with an exhaustive
# search on "h_grid" (chosen adaptatively from the sample) and optionally
# plots the BCV curve with "plot_cv"
bw.bcv.mod <- function(x, nb = 1000L,
                       h_grid = 10^seq(-3, log10(1.2 * sd(x) *
                                                   length(x)^(-1/5)), l = 200),
                       plot_cv = FALSE) {
  if ((n <- length(x)) < 2L)
    stop("need at least 2 data points")
  n <- as.integer(n)
  if (is.na(n))
    stop("invalid length(x)")
  if (!is.numeric(x))
    stop("invalid 'x'")
  nb <- as.integer(nb)
  if (is.na(nb) || nb <= 0L)
    stop("invalid 'nb'")
  storage.mode(x) <- "double"
  hmax <- 1.144 * sqrt(var(x)) * n^(-1/5)
  Z <- .Call(stats:::C_bw_den, nb, x)
  d <- Z[[1L]]
  cnt <- Z[[2L]]
  fbcv <- function(h) .Call(stats:::C_bw_bcv, n, d, cnt, h)
  ## Original code
  # h <- optimize(fbcv, c(lower, upper), tol = tol)$minimum
  # if (h < lower + tol | h > upper - tol)
  #   warning("minimum occurred at one end of the range")
  ## Modification
  obj <- sapply(h_grid, function(h) fbcv(h))
  h <- h_grid[which.min(obj)]
  if (h %in% range(h_grid)) 
    warning("minimum occurred at one end of h_grid")
  if (plot_cv) {
    plot(h_grid, obj, type = "o")
    rug(h_grid)
    abline(v = h, col = 2, lwd = 2)
  }
  h
}

# Compute the bandwidth and plot the BCV curve
bw.bcv.mod(x = x, plot_cv = TRUE, h_grid = 10^seq(-1.25, 0.5, l = 200))
## [1] 0.5111433

# We can compare with the default bw.bcv output
abline(v = bw.bcv(x = x), col = 3)

Figure 2.10: BCV curve evaluated for a grid of bandwidths, with a clear local minimum corresponding to \(\hat{h}_\mathrm{BCV}.\) Observe the decreasing pattern when \(h\to\infty.\)

2.4.3 Comparison of bandwidth selectors

Next, we state some insights from the convergence results of the DPI, LSCV, and BCV selectors. All of them are based on results of the kind

\[\begin{align} n^\nu(\hat{h}/h_\mathrm{MISE}-1)\stackrel{d}{\longrightarrow}\mathcal{N}(0,\sigma^2),\tag{2.31} \end{align}\]

where \(\sigma^2\) depends on \(K\) and \(f\) only, and measures how variable the selector is. The rate \(n^\nu\) serves to quantify how fast⁴⁸ the relative error \(\hat{h}/h_\mathrm{MISE}-1\) decreases (the larger the \(\nu,\) the faster the convergence).

Under certain regularity conditions, we have:

• \(n^{1/10}(\hat{h}_\mathrm{LSCV}/h_\mathrm{MISE}-1)\stackrel{d}{\longrightarrow}\mathcal{N}(0,\sigma_\mathrm{LSCV}^2)\) and \(n^{1/10}(\hat{h}_\mathrm{BCV}/h_\mathrm{MISE}-1)\stackrel{d}{\longrightarrow}\mathcal{N}(0,\sigma_\mathrm{BCV}^2).\) Both cross-validation selectors have a slow rate of convergence.⁴⁹ Inspection of the variances of both selectors reveals that, for the normal kernel, \(\sigma_\mathrm{LSCV}^2/\sigma_\mathrm{BCV}^2\approx 15.7.\) Therefore, LSCV is considerably more variable than BCV.

• \(n^{5/14}(\hat{h}_\mathrm{DPI}/h_\mathrm{MISE}-1)\stackrel{d}{\longrightarrow}\mathcal{N}(0,\sigma_\mathrm{DPI}^2).\) Thus, the DPI selector has a convergence rate much faster than the cross-validation selectors. There is an appealing explanation for this phenomenon. Recall that \(\hat{h}_\mathrm{BCV}\) minimizes the slightly modified version of \(\mathrm{BCV}(h)\) given by

  \[\begin{align*} \frac{1}{4}\mu_2^2(K)\tilde\psi_4(h)h^4+\frac{R(K)}{nh} \end{align*}\]

  and

  \[\begin{align*} \tilde\psi_4(h):=&\frac{1}{n(n-1)}\sum_{i=1}^n\sum_{\substack{j=1\\j\neq i}}^n(K_h''*K_h'')(X_i-X_j)\nonumber\\ =&\frac{n}{n-1}\widetilde{R(f'')}. \end{align*}\]

  \(\tilde\psi_4\) is a leave-out-diagonals estimate of \(\psi_4.\) Despite being different from \(\hat\psi_4,\) it serves for building a DPI analogous to BCV that points towards the precise fact that drags down the performance of BCV. The modified version of the DPI minimizes

  \[\begin{align*} \frac{1}{4}\mu_2^2(K)\tilde\psi_4(g)h^4+\frac{R(K)}{nh}, \end{align*}\]

  where \(g\) is independent of \(h.\) The two methods differ in the way \(g\) is chosen: BCV sets \(g=h\) and the modified DPI looks for the best \(g\) in terms of the \(\mathrm{AMSE}[\tilde\psi_4(g)].\) It can be seen that \(g_\mathrm{AMSE}=O(n^{-2/13}),\) whereas the \(h\) used in BCV is asymptotically \(O(n^{-1/5}).\) This suboptimality on the choice of \(g\) is the reason of the asymptotic deficiency of BCV.

We now focus on exploring the empirical performance of bandwidth selectors. The workhorse for doing that is simulation. A popular collection of simulation scenarios was given by Marron and Wand (1992) and is conveniently available through the package nor1mix. This collection is formed by normal \(m\)-mixtures of the form

\[\begin{align} f(x;\boldsymbol{\mu},\boldsymbol{\sigma},\mathbf{w}):&=\sum_{j=1}^m w_j\phi_{\sigma_j}(x-\mu_j), \tag{2.32} \end{align}\]

where \(w_j\geq0,\) \(j=1,\ldots,m\) and \(\sum_{j=1}^m w_j=1.\) Densities of this form are especially attractive since they allow for arbitrary flexibility and, if the normal kernel is employed, they allow for explicit and exact MISE expressions:

\[\begin{align} \begin{split} \mathrm{MISE}_m[\hat{f}(\cdot;h)]&=(2\sqrt{\pi}nh)^{-1}+\mathbf{w}'\{(1-n^{-1})\boldsymbol{\Omega}_2-2\boldsymbol{\Omega}_1+\boldsymbol{\Omega}_0\}\mathbf{w},\\ (\boldsymbol{\Omega}_a)_{ij}&=\phi_{(ah^2+\sigma_i^2+\sigma_j^2)^{1/2}}(\mu_i-\mu_j),\quad i,j=1,\ldots,m. \end{split} \tag{2.33} \end{align}\]

These exact MISE expressions are highly convenient for computing \(h_\mathrm{MISE},\) as defined in (2.22), by minimizing (2.33) numerically.

# Available models
?nor1mix::MarronWand

# Simulating
samp <- nor1mix::rnorMix(n = 500, obj = nor1mix::MW.nm9)
# MW object in the second argument
hist(samp, freq = FALSE)

# Density evaluation
x <- seq(-4, 4, length.out = 400)
lines(x, nor1mix::dnorMix(x = x, obj = nor1mix::MW.nm9), col = 2)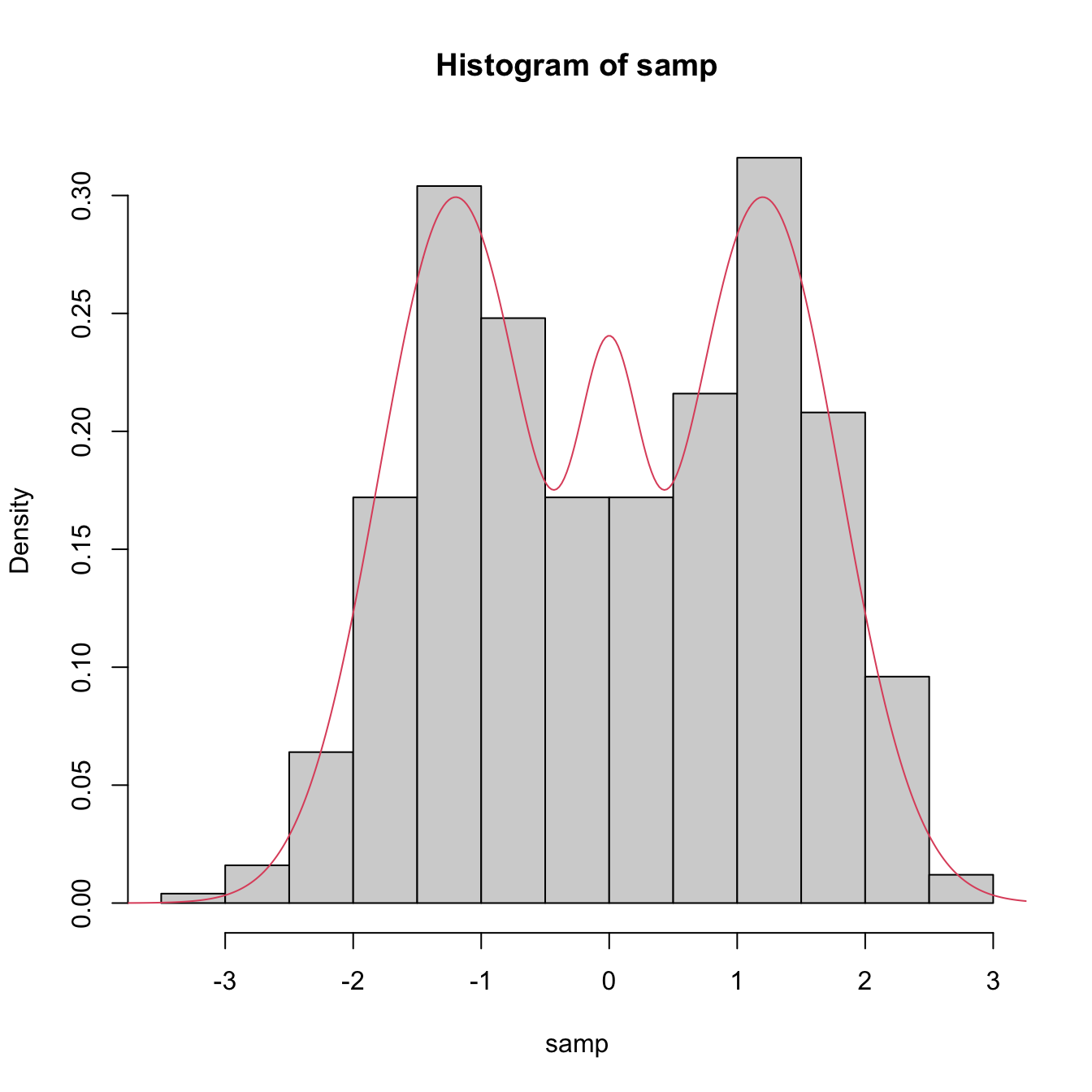

# Plot a MW object directly
# A normal with the same mean and variance is plotted in dashed lines --
# you can remove it with argument p.norm = FALSE
par(mfrow = c(2, 2))
plot(nor1mix::MW.nm5)
plot(nor1mix::MW.nm7)
plot(nor1mix::MW.nm10)
plot(nor1mix::MW.nm12)
lines(nor1mix::MW.nm7, col = 2) # Also possible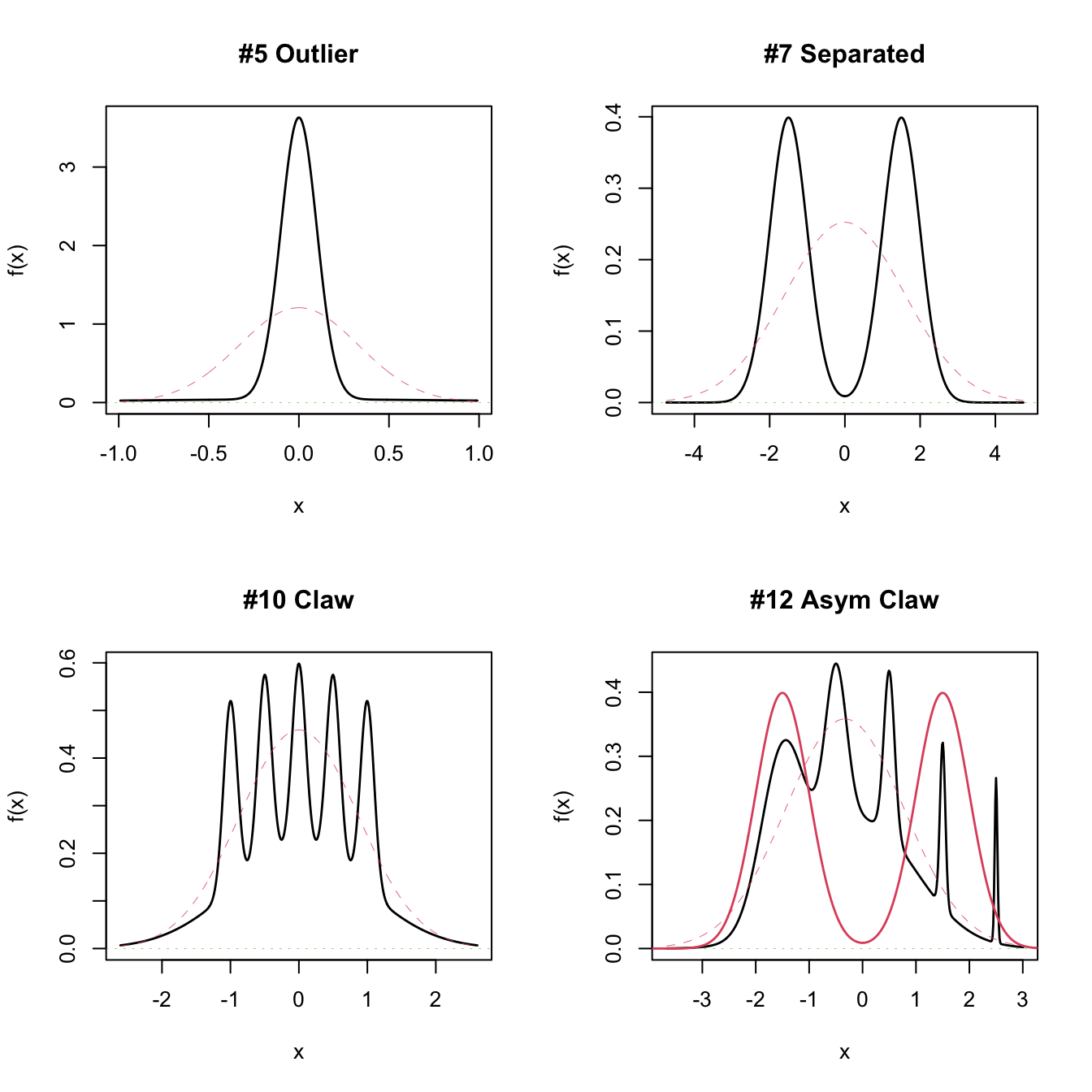

Exercise 2.18 Implement the \(h_\mathrm{MISE}\) using (2.22) and (2.33) for model nor1mix::MW.nm6. Then, compute by Monte Carlo the densities of \(\hat{h}_\mathrm{DPI}/h_\mathrm{MISE}-1,\) \(\hat{h}_\mathrm{LSCV}/h_\mathrm{MISE}-1,\) and \(\hat{h}_\mathrm{BCV}/h_\mathrm{MISE}-1.\) Compare them for \(n=100,200,500.\) Describe in detail the results and the major takeaways in relation to the properties of the bandwidth selectors.

Exercise 2.19 Compare the MISE and AMISE criteria in three densities in nor1mix of your choice. To that purpose, code (2.33) and the AMISE expression for the normal kernel, and compare the two error curves. Compare them for \(n=100,200,500,\) adding a vertical line to represent the \(h_\mathrm{MISE}\) and \(h_\mathrm{AMISE}\) bandwidths. Describe in detail the results and the major takeaways in relation to using \(h_\mathrm{AMISE}\) as a proxy for \(h_\mathrm{MISE}\).

A key practical issue that emerges after discussing several bandwidth selectors is the following:

Which bandwidth selector is the most adequate for a given dataset?

Unfortunately, there is no simple and universal answer to this question. There are, however, a series of useful facts and suggestions:

• Trying several selectors and inspecting the results may help to determine which one is estimating the density better.
• The DPI selector has a convergence rate much faster than the cross-validation selectors. Therefore, in theory it is expected to perform better than LSCV and BCV. For this reason, it tends to be among the preferred bandwidth selectors in the literature.
• Cross-validatory selectors may be better suited for highly non-normal and rough densities, in which plug-in selectors may end up oversmoothing.
• LSCV tends to be considerably more variable than BCV.
• The RT is a quick, simple, and inexpensive selector. However, it tends to give bandwidths that are too large for non-normal-like data.

Figure 2.11 presents a visualization of the performance of the kde with different bandwidth selectors, carried out in the family of mixtures by Marron and Wand (1992).

Figure 2.11: Performance comparison of bandwidth selectors. The RT, DPI, LSCV, and BCV are computed for each sample for a normal mixture density. For each sample, the animation computes the ISEs of the selectors and sorts them from best to worst. Changing the scenarios gives insight into the adequacy of each selector to hard- and simple-to-estimate densities. Application available here.

References

Devroye, L., and L. Györfi. 1985. Nonparametric Density Estimation. Wiley Series in Probability and Mathematical Statistics. New York: John Wiley & Sons. https://www.szit.bme.hu/~gyorfi/L1bookBW.pdf.

Marron, J. S., and M. P. Wand. 1992. “Exact Mean Integrated Squared Error.” The Annals of Statistics 20 (2): 712–36. https://doi.org/10.1214/aos/1176348653.

Scott, D. W. 2015. Multivariate Density Estimation. Second. Wiley Series in Probability and Statistics. Hoboken: John Wiley & Sons. https://doi.org/10.1002/9781118575574.

Scott, D. W., and G. R. Terrell. 1987. “Biased and Unbiased Cross-Validation in Density Estimation.” Journal of the American Statistical Association 82 (400): 1131–46. https://doi.org/10.1080/01621459.1987.10478550.

Sheather, S. J., and M. C. Jones. 1991. “A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.” Journal of the Royal Statistical Society, Series B (Methodological) 53 (3): 683–90. https://doi.org/10.1111/j.2517-6161.1991.tb01857.x.

Wand, M. P., and M. C. Jones. 1995. Kernel Smoothing. Vol. 60. Monographs on Statistics and Applied Probability. London: Chapman & Hall. https://doi.org/10.1201/b14876.

---

37. For defining \(\hat g(y;h)\) we consider the transformed kde seen in Section 2.5.1.↩︎

38. Since \(n^{-4/5}=o(n^{-2/3}).\)↩︎

39. We only use a parametric assumption for estimating the curvature of \(f\) in present \(h_\mathrm{AMISE},\) not for directly estimating \(f\) itself.↩︎

40. Not to confuse with bw.nrd0!↩︎

41. See Section 3.5 in Wand and Jones (1995) for full details.↩︎

42. Recall there is no “I”, since we are estimating a scalar, not a function.↩︎

43. For the rule-of-thumb selector, \(\ell=0\) and we estimate \(\psi_{4}\) parametrically. If \(\ell=2,\) we estimate \(\psi_{8}\) parametrically, which is then required for estimating \(\psi_{6}\) nonparametrically.↩︎

44. Hence, what we are doing is “sweeping under \(\ell\) nonparametric carpets” this parametric estimate on the characteristic \(\psi_{\ell+4}\) of the density, ultimately required for computing the bandwidth selector.↩︎

45. Why so? Because \(X\) is unbiased for estimating \(\mathbb{E}[X].\)↩︎

46. Long intervals containing the solution may lead to unsatisfactory termination of the search; short intervals might not contain the minimum.↩︎

47. The precise point at which a bandwidth is “too big” can be formalized with the maximal smoothing principle, as elaborated in Section 3.2.2 in Wand and Jones (1995).↩︎

48. Recall that another way of writing (2.31) is as the relative error \(\frac{\hat{h}-h_\mathrm{MISE}}{h_\mathrm{MISE}}\) being asymptotically distributed as a \(\mathcal{N}\left(0,\frac{\sigma^2}{n^{2\nu}}\right).\)↩︎

49. Compare it with the \(n^{1/2}\) rate of the CLT!↩︎