2.3 Asymptotic properties
Asymptotic results serve the purpose of establishing the large-sample (\(n\to\infty\)) properties of an estimator. One might question why they are useful, since in practice we only have finite sample sizes. Apart from purely theoretical reasons, asymptotic results usually give highly valuable insights into the properties of the estimator, typically much simpler to grasp than those obtained from finite-sample results.29
Throughout this section we will make the following assumptions:
- A1.30 The density \(f\) is square integrable, twice continuously differentiable, and the second derivative is square integrable.
- A2.31 The kernel \(K\) is a symmetric and bounded pdf with finite second moment and square integrable.
- A3.32 \(h=h_n\) is a deterministic sequence of positive scalars33 such that, when \(n\to\infty,\) \(h\to0\) and \(nh\to\infty.\)
We need to introduce some notation. The squared integral of a function \(f\) is denoted by \(R(f):=\int f(x)^2\,\mathrm{d}x.\) The convolution between two real functions \(f\) and \(g,\) \(f*g,\) is the function
\[\begin{align} (f*g)(x):=\int f(x-y)g(y)\,\mathrm{d}y=(g*f)(x).\tag{2.10} \end{align}\]
We are now ready to obtain the bias and variance of \(\hat{f}(x;h).\) Recall that is not possible to apply the “binomial trick” we used previously for the histogram and moving histogram: now the estimator is not piecewise constant. Instead, we use the linearity of the kde and the convolution definition. For the expectation, we have
\[\begin{align} \mathbb{E}[\hat{f}(x;h)]&=\frac{1}{n}\sum_{i=1}^n\mathbb{E}[K_h(x-X_i)]\nonumber\\ &=\int K_h(x-y)f(y)\,\mathrm{d}y\nonumber\\ &=(K_h * f)(x).\tag{2.11} \end{align}\]
Similarly, the variance is obtained as
\[\begin{align} \mathbb{V}\mathrm{ar}[\hat{f}(x;h)]&=\frac{1}{n}((K_h^2*f)(x)-(K_h*f)^2(x)).\tag{2.12} \end{align}\]
These two expressions are exact, but hard to interpret. Equation (2.11) indicates that the estimator is biased,34 but it does not explicitly differentiate the effects of kernel, bandwidth, and density on the bias. The same happens with (2.12), yet more emphasized. Clarity is why the following asymptotic expressions are preferred.
Theorem 2.1 Under A1–A3, the bias and variance of the kde at \(x\) are
\[\begin{align} \mathrm{Bias}[\hat{f}(x;h)]&=\frac{1}{2}\mu_2(K)f''(x)h^2+o(h^2),\tag{2.13}\\ \mathbb{V}\mathrm{ar}[\hat{f}(x;h)]&=\frac{R(K)}{nh}f(x)+o((nh)^{-1}).\tag{2.14} \end{align}\]
Proof. For the bias we consider the change of variables \(z=\frac{x-y}{h},\) \(y=x-hz,\) \(\mathrm{d}y=-h\,\mathrm{d}z.\) The integral limits flip and we have
\[\begin{align} \mathbb{E}[\hat{f}(x;h)]&=\int K_h(x-y)f(y)\,\mathrm{d}y\nonumber\\ &=\int K(z)f(x-hz)\,\mathrm{d}z.\tag{2.15} \end{align}\]
Since \(h\to0,\) an application of a second-order Taylor expansion gives
\[\begin{align} f(x-hz)=&\,f(x)-f'(x)hz+\frac{f''(x)}{2}h^2z^2\nonumber\\ &+o(h^2z^2). \tag{2.16} \end{align}\]
Substituting (2.16) in (2.15), and bearing in mind that \(K\) is a symmetric density about \(0,\) we have
\[\begin{align*} \int K(z)&f(x-hz)\,\mathrm{d}z\\ =&\,\int K(z)\Big\{f(x)-f'(x)hz+\frac{f''(x)}{2}h^2z^2\\ &+o(h^2z^2)\Big\}\,\mathrm{d}z\\ =&\,f(x)+\frac{1}{2}\mu_2(K)f''(x)h^2+o(h^2), \end{align*}\]
which provides (2.13).
For the variance, first note that
\[\begin{align} \mathbb{V}\mathrm{ar}[\hat{f}(x;h)]&=\frac{1}{n^2}\sum_{i=1}^n\mathbb{V}\mathrm{ar}[K_h(x-X_i)]\nonumber\\ &=\frac{1}{n}\left\{\mathbb{E}[K_h^2(x-X)]-\mathbb{E}[K_h(x-X)]^2\right\}. \tag{2.17} \end{align}\]
The second term of (2.17) is already computed, so we focus on the first. Using the previous change of variables and a first-order Taylor expansion, we have
\[\begin{align} \mathbb{E}[K_h^2(x-X)]&=\frac{1}{h}\int K^2(z)f(x-hz)\,\mathrm{d}z\nonumber\\ &=\frac{1}{h}\int K^2(z)\left\{f(x)+O(hz)\right\}\,\mathrm{d}z\nonumber\\ &=\frac{R(K)}{h}f(x)+O(1). \tag{2.18} \end{align}\]
Plugging (2.17) into (2.18) gives
\[\begin{align*} \mathbb{V}\mathrm{ar}[\hat{f}(x;h)]&=\frac{1}{n}\left\{\frac{R(K)}{h}f(x)+O(1)-O(1)\right\}\\ &=\frac{R(K)}{nh}f(x)+O(n^{-1})\\ &=\frac{R(K)}{nh}f(x)+o((nh)^{-1}), \end{align*}\]
since \(n^{-1}=o((nh)^{-1}).\)
Remark. Integrating little-\(o\)’s is a tricky issue. In general, integrating a \(o^x(1)\) quantity, possibly dependent on \(x\) (this is emphasized with the superscript), does not provide an \(o(1).\) In other words: \(\int o^x(1)\,\mathrm{d}x\neq o(1).\) If the previous inequality becomes an equality, then the limits and integral will be interchangeable. But this is not always true – only if certain conditions are met, recall the DCT (Theorem 1.12). If one wants to be completely rigorous on the two implicit commutations of integrals and limits that took place in the proof, it is necessary to have explicit control of the remainder via Taylor’s theorem (Theorem 1.11) and then apply the DCT. This has been skipped for simplicity in the exposition.
The bias and variance expressions (2.13) and (2.14) yield interesting insights (see Figure 2.5 for visualizations thereof):
The bias decreases with \(h\) quadratically. In addition, the bias at \(x\) is directly proportional to \(f''(x).\) This has an interesting interpretation:
- The bias is negative where \(f\) is concave, i.e., \(\{x\in\mathbb{R}:f''(x)<0\}.\) These regions correspond to peaks and modes of \(f,\) where the kde underestimates \(f\) (it tends to be below \(f\)).
- Conversely, the bias is positive where \(f\) is convex, i.e., \(\{x\in\mathbb{R}:f''(x)>0\}.\) These regions correspond to valleys and tails of \(f,\) where the kde overestimates \(f\) (it tends to be above \(f\)).
- The “wilder” the curvature \(f'',\) the harder to estimate \(f.\) Flat density regions are easier to estimate than wiggling regions with high curvature (e.g., with several modes).
The variance depends directly on \(f(x).\) The higher the density, the more variable is the kde. Interestingly, the variance decreases as a factor of \((nh)^{-1},\) a consequence of \(nh\) playing the role of the effective sample size for estimating \(f(x).\) The effective sample size can be thought of as the amount of data35 in the neighborhood of \(x\) that is employed for estimating \(f(x).\)
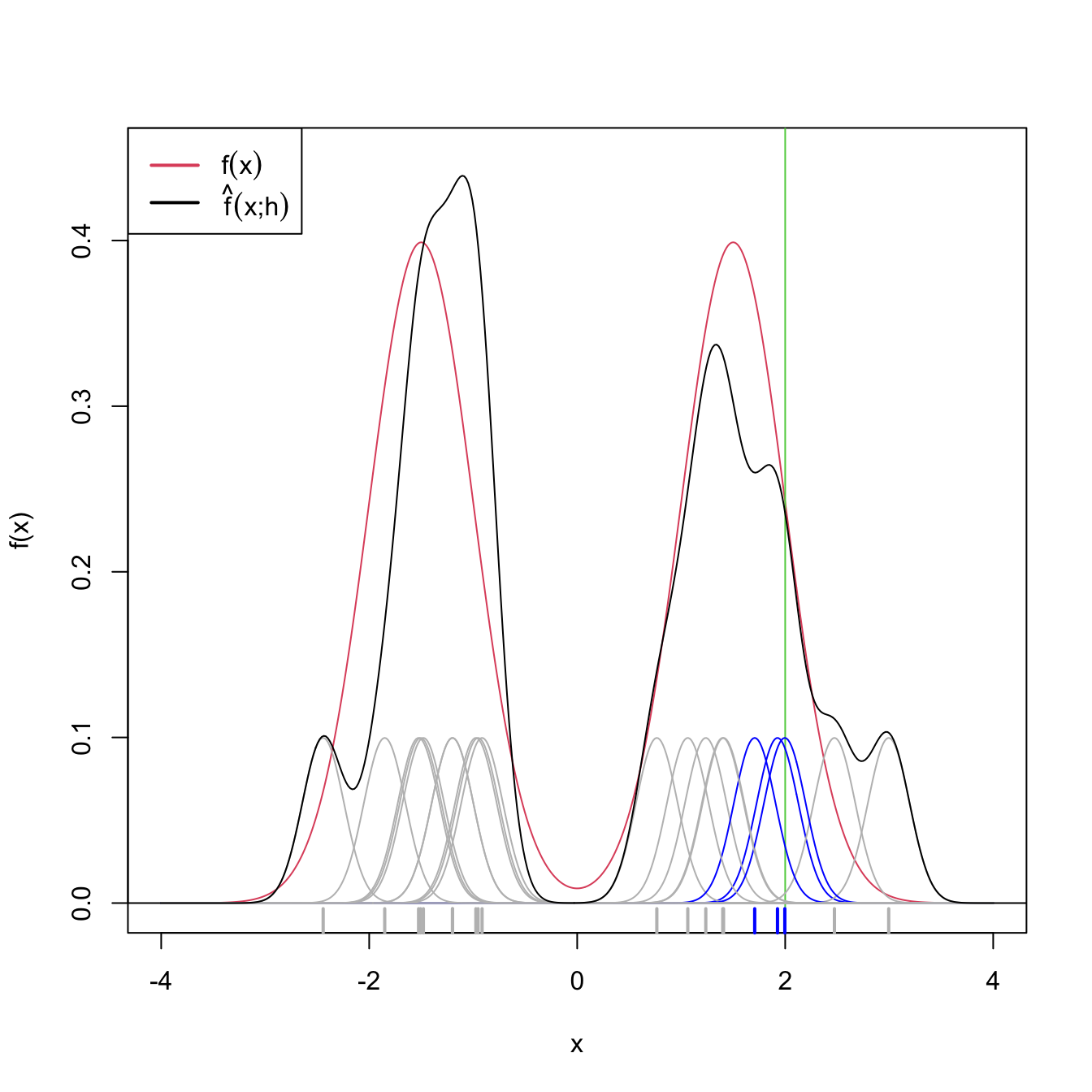
Figure 2.8: Illustration of the effective sample size for estimating \(f(x)\) at \(x=2.\) In blue, the kernels with contribution to the kde larger than \(0.01.\) In gray, rest of the kernels. Only \(3\) observations are effectively employed for estimating \(f(2)\) by \(\hat f(2;0.2),\) despite the sample size being \(n=20\).
Exercise 2.10 Using Example 1.5 and Theorem 2.1, show that:
- \(\hat{f}(x;h)=f(x)+O(h^2)+O_\mathbb{P}\big((nh)^{-1/2}\big).\)
- \(\hat{f}(x;h)=f(x)(1+o_\mathbb{P}(1)).\)
The MSE of the kde is trivial to obtain from the bias and variance.
Corollary 2.1 Under A1–A3, the MSE of the kde at \(x\) is
\[\begin{align} \mathrm{MSE}[\hat{f}(x;h)]=\,&\frac{\mu^2_2(K)}{4}(f''(x))^2h^4+\frac{R(K)}{nh}f(x)\nonumber\\ &+o(h^4+(nh)^{-1}).\tag{2.19} \end{align}\]
Therefore, the kde is pointwise consistent in MSE, i.e., \(\hat{f}(x;h)\stackrel{2}{\longrightarrow}f(x).\)
Note that, due to the MSE-consistency of \(\hat{f}(x;h),\) \[\begin{align*} \hat{f}(x;h)\stackrel{2}{\longrightarrow}f(x)\implies\hat{f}(x;h)\stackrel{\mathbb{P}}{\longrightarrow}f(x)\implies\hat{f}(x;h)\stackrel{d}{\longrightarrow}f(x) \end{align*}\] under A1–A2. However, these results are not useful for quantifying the randomness of \(\hat{f}(x;h)\): the convergence is towards the degenerate random variable \(f(x),\) for a given \(x\in\mathbb{R}.\)36 For that reason, we now turn our attention to the asymptotic normality of the estimator.
Theorem 2.2 Assume that \(\int K^{2+\delta}(z)\,\mathrm{d}z<\infty\,\)37 for some \(\delta>0.\) Then, under A1–A3,
\[\begin{align} &\sqrt{nh}\left(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)]\right)\stackrel{d}{\longrightarrow}\mathcal{N}(0,R(K)f(x)).\tag{2.20} \end{align}\]
Additionally, if \(nh^5=O(1),\) then
\[\begin{align} &\sqrt{nh}\left(\hat{f}(x;h)-f(x)-\frac{1}{2}\mu_2(K)f''(x)h^2\right)\stackrel{d}{\longrightarrow}\mathcal{N}(0,R(K)f(x)).\tag{2.21} \end{align}\]
Proof. First note that \(K_h(x-X_n)\) is a sequence of independent but not identically distributed random variables: \(h=h_n\) depends on \(n.\) Therefore, we look forward to applying Theorem 1.3.
We first prove (2.20). For simplicity, denote \(K_i:=K_h(x-X_i),\) \(i=1,\ldots,n.\) From the proof of Theorem 2.1 we know that \(\mathbb{E}[K_i]=\mathbb{E}[\hat{f}(x;h)]=f(x)+o(1)\) and
\[\begin{align*} s_n^2&=\sum_{i=1}^n \mathbb{V}\mathrm{ar}[K_i]\\ &=n^2\mathbb{V}\mathrm{ar}[\hat{f}(x;h)]\\ &=n\frac{R(K)}{h}f(x)(1+o(1)). \end{align*}\]
An application of the \(C_p\) inequality of Lemma 1.1 (first) and Jensen’s inequality (second), gives
\[\begin{align*} \mathbb{E}\left[|K_i-\mathbb{E}[K_i]|^{2+\delta}\right]&\leq C_{2+\delta}\left(\mathbb{E}\left[|K_i|^{2+\delta}\right]+|\mathbb{E}[K_i]|^{2+\delta}\right)\\ &\leq 2C_{2+\delta}\mathbb{E}\left[|K_i|^{2+\delta}\right]\\ &=O\left(\mathbb{E}\left[|K_i|^{2+\delta}\right]\right). \end{align*}\]
In addition, due to a Taylor expansion after \(z=\frac{x-y}{h}\) and using that \(\int K^{2+\delta}(z)\,\mathrm{d}z<\infty,\)
\[\begin{align*} \mathbb{E}\left[|K_i|^{2+\delta}\right]&=\frac{1}{h^{2+\delta}}\int K^{2+\delta}\left(\frac{x-y}{h}\right)f(y)\,\mathrm{d}y\\ &=\frac{1}{h^{1+\delta}}\int K^{2+\delta}(z)f(x-hz)\,\mathrm{d}z\\ &=\frac{1}{h^{1+\delta}}\int K^{2+\delta}(z)(f(x)+o(1))\,\mathrm{d}z\\ &=O\left(h^{-(1+\delta)}\right). \end{align*}\]
Then,
\[\begin{align*} \frac{1}{s_n^{2+\delta}}&\sum_{i=1}^n\mathbb{E}\left[|K_i-\mathbb{E}[K_i]|^{2+\delta}\right]\\ &=\left(\frac{h}{nR(K)f(x)}\right)^{1+\frac{\delta}{2}}(1+o(1))O\left(nh^{-(1+\delta)}\right)\\ &=O\left((nh)^{-\frac{\delta}{2}}\right) \end{align*}\]
and the Lyapunov’s condition is satisfied. As a consequence, by Lyapunov’s CLT and Slutsky’s theorem,
\[\begin{align*} \sqrt{\frac{nh}{R(K)f(x)}}&(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)])\\ &=(1+o(1))\frac{1}{s_n}\sum_{i=1}^n(K_i-\mathbb{E}[K_i])\\ &\stackrel{d}{\longrightarrow}\mathcal{N}(0,1) \end{align*}\]
and (2.20) is proved.
To prove (2.21), we consider
\[\begin{align*} \sqrt{nh}&\left(\hat{f}(x;h)-f(x)-\frac{1}{2}\mu_2(K)f''(x)h^2\right)\\ &=\sqrt{nh}(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)]+o(h^2)). \end{align*}\]
Therefore, Slutsky’s theorem and the assumption \(nh^5=O(1)\) give
\[\begin{align*} \sqrt{nh}&(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)]+o(h^2))\\ &=\sqrt{nh}\left(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)]+o(\sqrt{nh^5})\right)\\ &=\sqrt{nh}\left(\hat{f}(x;h)-\mathbb{E}[\hat{f}(x;h)]\right)+o(1)\\ &\stackrel{d}{\longrightarrow}\mathcal{N}(0,R(K)f(x)). \end{align*}\]
Remark. Note the rate \(\sqrt{nh}\) in the asymptotic normality results. This is different from the standard CLT rate \(\sqrt{n}\) (see Theorem 1.2). Indeed, \(\sqrt{nh}\) is slower than \(\sqrt{n}\): the variance of the limiting normal distribution decreases as \(O((nh)^{-1})\) and not as \(O(n^{-1}).\) The phenomenon is related to the effective sample size previously illustrated with Figure 2.8.
Finite-sample results might be either analytically unfeasible or dependent on simulation studies that are necessarily limited in their scope.↩︎
This assumption requires certain smoothness of the pdf, allowing thus for Taylor expansions to be performed on \(f.\)↩︎
Mild assumption that makes the first term of the Taylor expansion of \(f\) negligible and the second one bounded.↩︎
The key assumption for reducing the bias and variance of \(\hat{f}(\cdot;h)\) simultaneously.↩︎
\(h=h_n\) always depends on \(n\) from now on, although the subscript is dropped for the ease of notation.↩︎
Since \(\mathrm{Bias}[\hat{f}(x;h)]=(K_h*f)(x)-f(x)\neq 0.\) An example of this bias in given in Section A.↩︎
The variance of an unweighted mean is reduced by a factor \(n^{-1}\) when \(n\) observations are employed. For computing \(\hat{f}(x;h),\) \(n\) observations are used but in a weighted fashion that roughly amounts to considering \(nh\) unweighted observations.↩︎
That is, towards the random variable that always takes the value \(f(x).\)↩︎
This is satisfied, for example, if the kernel decreases exponentially, i.e., if \(\exists\, \alpha,\,M>0: K(z)\leq e^{-\alpha|z|},\,\forall|z|>M.\)↩︎