Chapter 38: GLM

An introduction to Generalized Linear Models.

Motivating scenario: We want to model nonlinear data. Here we use yes/no (or proportion) data as an example.

Review

Linear models and their assumptions

A statistical model describes the predicted value of a response variable as a function of one or more explanatory variables.

A linear model predicts the response variable by adding up all components of the model. So, In a linear model, we predict the value of a response variable, \(\widehat{Y_i}\) knowing that the observed value, \(Y_i\) will deviate from this prediction by some normally distributed “residual” value, \(e_i\).

\[Y_i = \widehat{Y_i} -e_i\]

We predict Y as a deviation from some constant, a, as a function of a bunch of stuff.

\[\widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times y_{2,i} + \dots\]

Assumptions of Linear Models

Linear models assume

When data do not meet assumptions

If data do not meet assumptions, we can forge ahead (if the test will be robust), permute/bootstrap, transform, or find a better model.

Common violations

We know that a lot of real-world data can be modeled by a linear model, and we also know that the linear model is relatively robust to violations of its assumptions.

Still, there are some relatively violations of assumptions of linear models that are particularly common, especially in biological data.

How biology breaks assumptions of the linear model (better approach in parentheses):

Likelihood-Based Inference

We have previously seen the idea of likelihood-based inference, which we can use to infer parameters, estimate uncertainty, and test null hypotheses for any data that we can appropriately model. We previously used likelihood for our familiar linear models. That is we could have done without the likelihood approach. Here, we’ll show the true strength of likelihood-based inference – its flexibility.

Generalized Linear Models

Generalized Linear Models (GLMs) allow us to model non-linear data by modeling data the way it is distributed. They do so by:

  1. Specifying the distribution family they come from (the random component).
  2. Finding a “linear predictor” (systematic component).
  3. Using a link function to translate from linear predictor to the data.

What does this mean? Let’s look at the example below to clarify!

Today we focus on logistic regression (usd for yes/no) data. However, we can use a generalized linear model to model data from any distribution. We will skip poisson regression (used for count data) this year, but **check out last years chapter on poisson regression if you want more!!!!

Assumptions of generalized linear models

GLMs are flexible and allow us to model just about anything. But our models must be appropriate for our data. Specifically, GLMs assume

GLM Example: “logistic regression”

A particularly common type of biological data is yes / no data. Common examples of yes / no data are

Such data are poorly described by a standard linear model, but we can generalize the linear model to nonlinear data.. Logistic regression is a type of generalized linear model (GLM) which models a yes/no outcome as a function of a continuous predictor (e.g. win/lose, live/die, presence/absence). The linear predictor is the familiar regression equation:

\[\widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times y_{2,i} + \dots\]

\(\widehat{Y_i}\) is not our prediction for the probability of “yes”, \(\widehat{p_i}\). Rather, in a GLM, we use this “linear predictor” through the “link function” to find our prediction.

For a logistic regression, the “linear predictor” describes the log odds, which we can convert to the predicted probability of success, \(\widehat{p_i}\) with the logit link function. That is,

\[\widehat{p_i} = \frac{e^{Y_i}}{1+e^{Y_i}}\]
So if our link function says that the log-odds, \(\widehat{Y_i}\), equals negative one, the probability of “yes” is \(\frac{e^{-1}}{1+e^{-1}} = 0.269\). We can find this in R as

Logistic Regression Example: Cold fish

How does the length of exposure to cold water impact fish mortality? fish survive in cold weather?

Pitkow et al (1960) exposed guppies to 2, 8, 12, or 18 minutes in 5 degree Celsius water. The data – with a value of 1 for Alive meaning alive and a value of zero meaning dead – are presented below

cold.fish <- tibble(Time  = rep(c(2,8,12,18), times = 2),
                    Alive = rep(c(0,1), each = 4),
                    n     = c(11, 24, 29, 38, 29, 16, 11, 2)) %>%
  uncount(weights = n)

What to do??

(Imperfect) Option 1: Linear model with zero / one data

We could build a linear model in which we predict survival as a function of time in cold water.

ggplot(cold.fish, aes(x = Time, y = Alive)) + 
  geom_jitter(size = 2, alpha = .35, height = .05, width = .5)+
  geom_smooth(method = "lm")+
  scale_x_continuous(breaks = seq(2,18,6),limits = c(0,20))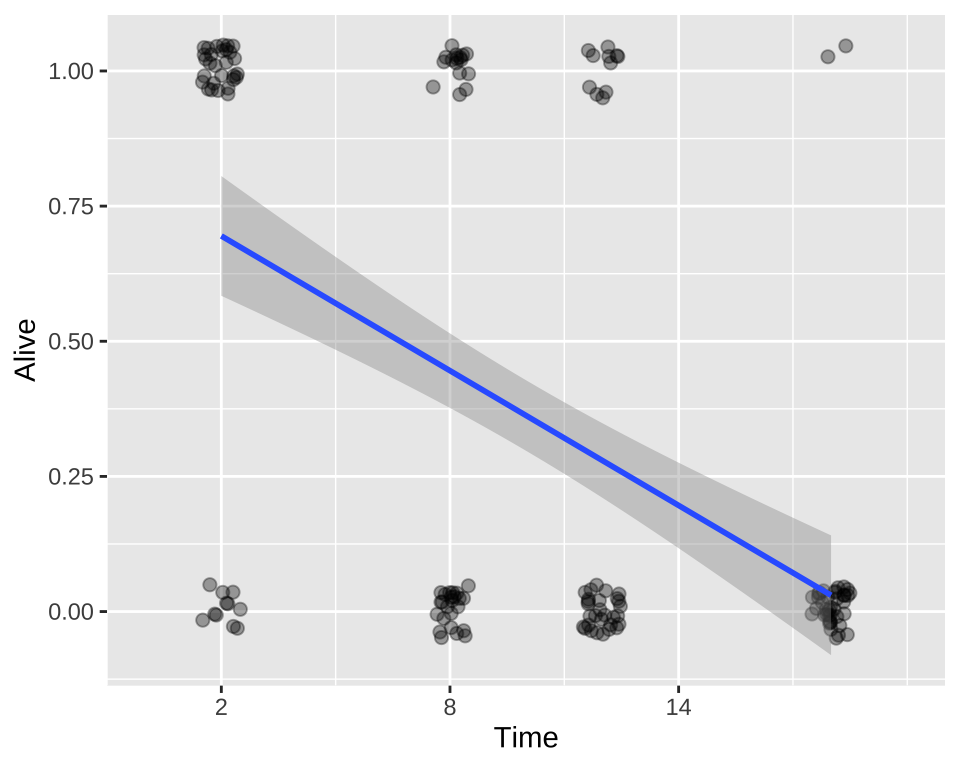

lm_cold_fish1 <- lm(Alive ~ Time, data = cold.fish)
summary.lm(lm_cold_fish1)

Call:
lm(formula = Alive ~ Time, data = cold.fish)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.69485 -0.27941 -0.03015  0.30515  0.96985 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.777941   0.065580  11.863  < 2e-16 ***
Time        -0.041544   0.005665  -7.333  1.1e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4178 on 158 degrees of freedom
Multiple R-squared:  0.2539,    Adjusted R-squared:  0.2492 
F-statistic: 53.78 on 1 and 158 DF,  p-value: 1.101e-11

We see – unsurprisingly, that fish survival strongly and significantly decreases, the longer they are in cold water.

autoplot(lm_cold_fish1 , ncol = 4)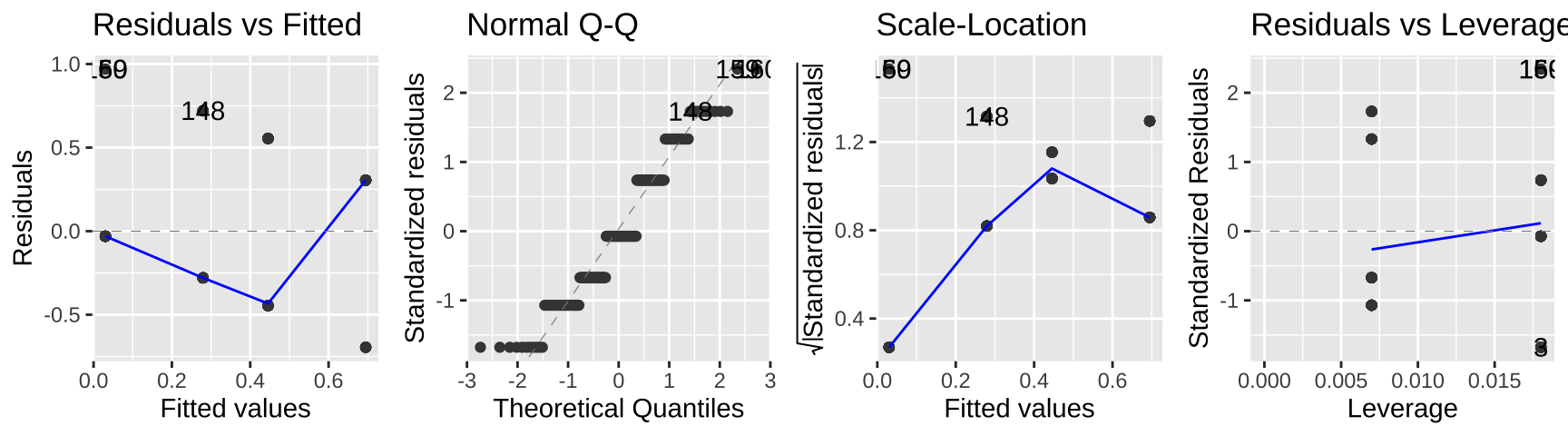

While this isn’t terrible, we do so greatest residuals for intermediate predictions, and the small values are too big (above the xy line) and large values are too big.

So, this isn’t the end of the world, but isn’t ideal.

(Imperfect) option 2: Linear model with proportions

Alternatively, we could convert data to proportions and run a linear model.

cold.fish.summary <- cold.fish %>% 
    group_by(Time, Alive) %>%
    summarise(n = n())    %>%
    mutate(n_tot = sum(n),
           prop_survive = n /n_tot)  %>%
    filter(Alive == 1) %>% 
    ungroup()
Time Alive n n_tot prop_survive
2 1 29 40 0.725
8 1 16 40 0.400
12 1 11 40 0.275
18 1 2 40 0.050 
lm_cold_fish2 <- lm(prop_survive ~ Time, cold.fish.summary)
summary.lm(lm_cold_fish2)

Call:
lm(formula = prop_survive ~ Time, data = cold.fish.summary)

Residuals:
        1         2         3         4 
 0.030147 -0.045588 -0.004412  0.019853 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)  0.777941   0.040931   19.01  0.00276 **
Time        -0.041544   0.003536  -11.75  0.00717 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.04124 on 2 degrees of freedom
Multiple R-squared:  0.9857,    Adjusted R-squared:  0.9786 
F-statistic:   138 on 1 and 2 DF,  p-value: 0.007166

We see – unsurprisingly, that fish survival strongly and significantly decreases (although the p-value is considerably greater than above), the longer they are in cold water.

autoplot(lm_cold_fish2, ncol = 4)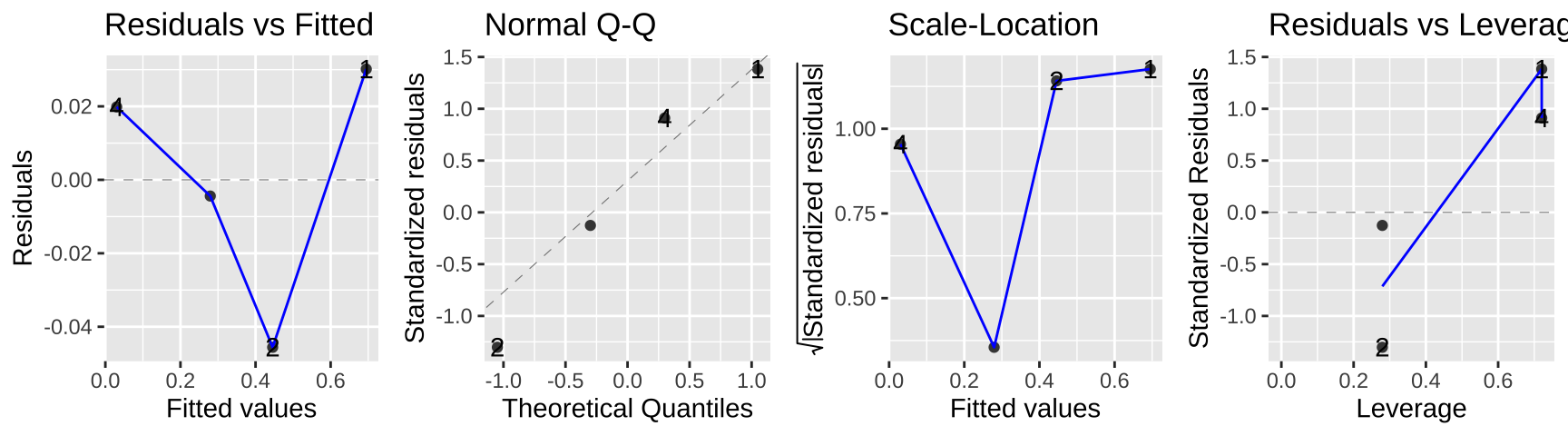

In this case the data seem to meet assumptions, but often they will not. In this case, a bigger issue is that we gave up a ton of power – we went from 160 to four data points. look ok…

(Better) option three – logistic regression

A better option is to model the data as they are – 160 observations of Alive or Dead with forty fish at four different temperatures.

Fitting the model

In R, do this with the glm() function, noting that the data are binomially distributed and that we want our link function to be the logit.

There are two equivalent ways to do this.

cold.fish.glm1 <- glm(prop_survive ~ Time, weights = n_tot, 
    data = cold.fish.summary, family = binomial(link = "logit"))
cold.fish.glm2 <- glm(prop_survive ~ Time, 
                       weights = n_tot, data = cold.fish.summary, 
                       family = binomial(link = "logit"))

Regardless, we get the same result for our estimates (and p-values). As in a linear model, we pay attention to the estimates but ignore the incorrect p-values below, and find the correct values with the anova function (see below).

summary.glm(cold.fish.glm1)

Call:
glm(formula = prop_survive ~ Time, family = binomial(link = "logit"), 
    data = cold.fish.summary, weights = n_tot)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.44470    0.37462   3.856 0.000115 ***
Time        -0.22191    0.03886  -5.711 1.12e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 45.72062  on 3  degrees of freedom
Residual deviance:  0.87086  on 2  degrees of freedom
AIC: 19.408

Number of Fisher Scoring iterations: 4

How can we take this output and predict the proportion of fish that will survive exposure to 4C water for some time? Say 6 minutes?

\[\widehat{Y_i} = 1.44470 -0.22191 \times Time\]
So we predict the log odds of a fish surviving following six minutes of exposure to 4C water to equal \(1.44470 - 6 \times 0.22191 = 0.11324\).

This does not mean that a fish has a 0.11324 probability of surviving six minutes of exposure to 4C water – this is just the log-odds of surviving. We convert this to a survival probability with the logit link function.

\[p_\text{survive six min} = \frac{e^{0.11324}}{1+e^{0.11324}} = 0.528\]

Or with plogis(), plogis(.11324) = 0.5282798.

This prediction – that a fish at 4C for six minutes has a 52.8% chance of surviving is in line with our plots while incorrectly interpreting the output of the linear predictor as the predicted proportion is not.

Testing the model

We formally test the null hypothesis by conducting a likelihood ratio test – that is, we take two times the difference in log-likelihoods and compare this value to its null sampling distribution (which happens to be a \(\chi^2\) distribution with degrees of freedom equal to the difference in the number of parameters estimated for the null and the fitted model).

We can do this with the anova function, telling R tht we want our test tb be the LRT (we get the same answer if we ask or a Chisq).

anova(cold.fish.glm1, test = "LRT")
Analysis of Deviance Table

Model: binomial, link: logit

Response: prop_survive

Terms added sequentially (first to last)

     Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                     3     45.721              
Time  1    44.85         2      0.871 2.127e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Plotting the model

We can add this fit to a plot!!!

For either the raw data

ggplot(cold.fish, aes(x = Time, y = Alive)) + 
  geom_jitter(size = 2, alpha = .35, height = .05, width = .5)+
  geom_smooth(method = "glm",method.args = list('binomial'))+
  scale_x_continuous(breaks = seq(2,18,6),limits = c(0,20))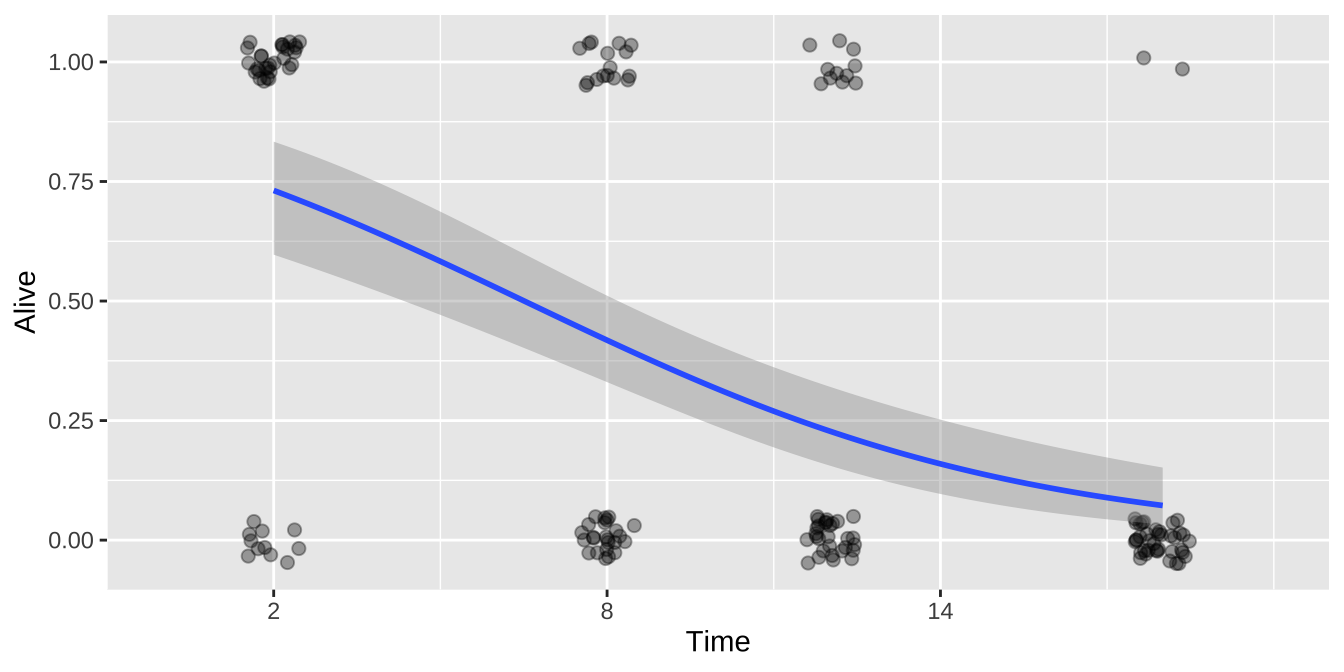

Or the summary

ggplot(cold.fish.summary, aes(x = Time, y = prop_survive, weight = n_tot)) + 
  geom_point(aes(size = n_tot))+
  geom_smooth(method = "glm",method.args = list('binomial'))+
  scale_x_continuous(breaks = seq(2,18,6),limits = c(0,20))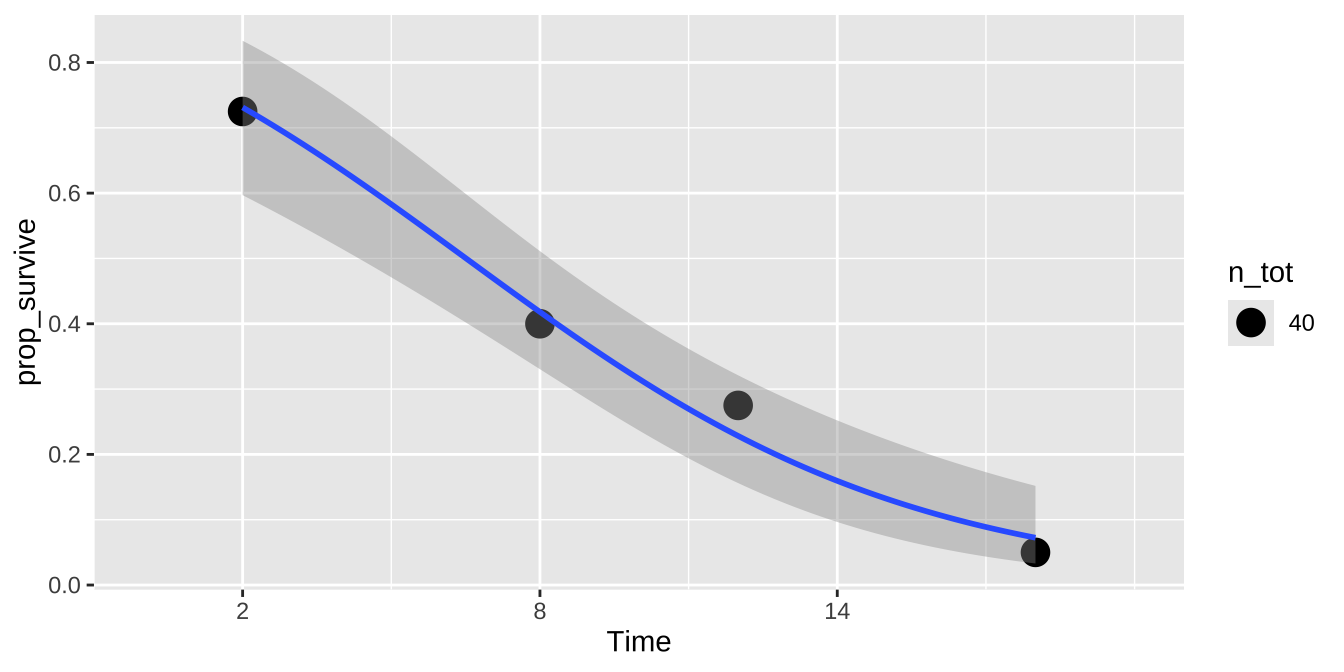

GLM Example 2: “Poisson regression” and count data

A particularly common type of biological data is count data. Common examples of count data are

Such data are poorly described by a standard linear model, but can be modeled. Below, I simulate leaves falling randomly on a landscape. We see that the number of leaves in each quadrant does not follow a normal distribution.

sim_rand_location <- tibble(x = runif(110), y = runif(110)) %>%
  mutate(x_box = cut(x, breaks = seq(0,1,.1)),
         y_box = cut(y, breaks = seq(0,1,.1)))

plot_location <- ggplot(sim_rand_location , aes(x = x, y = y, label = emoji("fallen_leaf"))) +
  geom_text(family="EmojiOne", color = "brown", hjust = 0.5, vjust = 0.5)+
  theme_tufte() +  geom_vline(xintercept = seq(0,1,.1), color = "black", alpha = .3)+ 
  geom_hline(yintercept = seq(0,1,.1), color = "black", alpha = .3)+
  scale_x_continuous(expand = c(0,0)) +    scale_y_continuous(expand = c(0,0)) 

location_histogram <- sim_rand_location %>% 
  group_by(x_box, y_box, .drop = FALSE) %>%
  summarise(n = n())     %>%
  ggplot(aes(x = n))+
  geom_histogram(binwidth = 1, color = "white", size = 2)+ 
  scale_x_continuous(breaks = seq(0,8,1))+
  theme_light()

plot_grid(plot_location, location_histogram, ncol =2)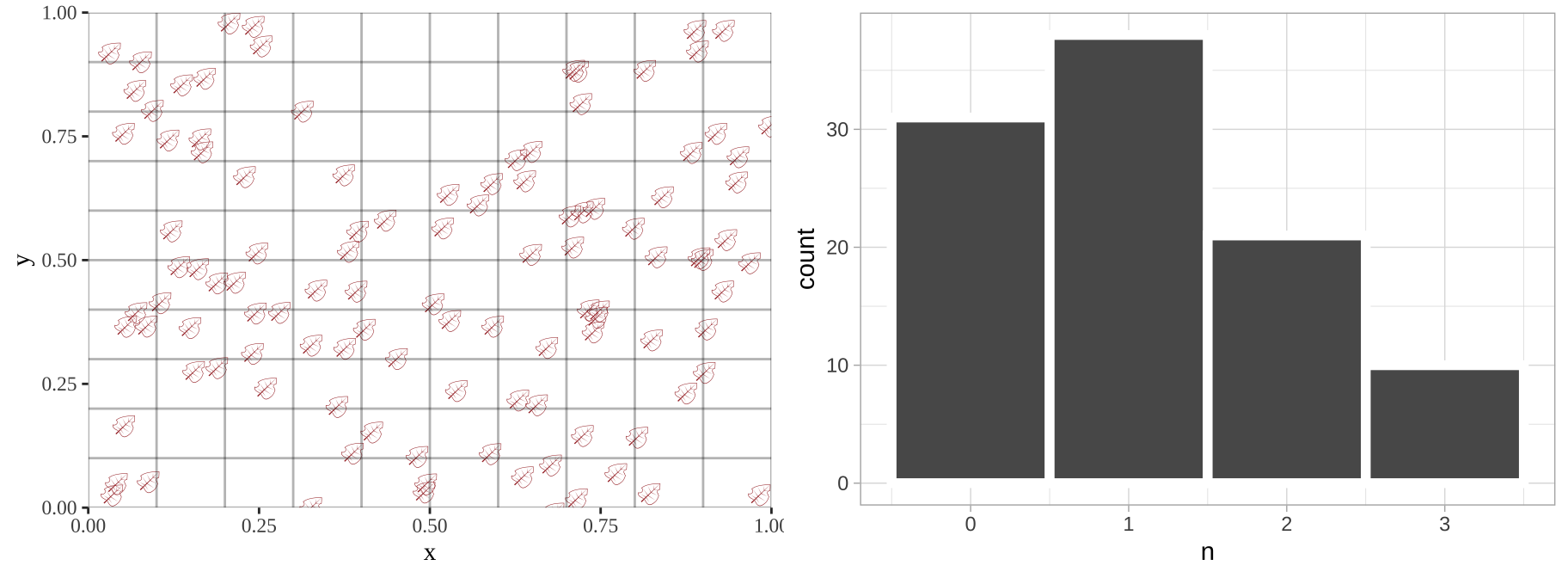

The poisson distribution

If these counts are randomly distributed over time or space, they will follow a Poisson distribution. For this reason, the Poisson is a common starting place for modeling count data.

If there are, on average, \(\lambda\) things per unit of time or space, the poisson equation predicts the probability the we have X things in one unit of time or space equals

\[P(X) = \frac{e^{-\lambda} \lambda^X}{X!}\] The mean of the Poisson is \(\lambda\), as is the variance. Because the variance increases with the mean, Poisson distributed data often violates the homoscedasticity assumption of linear models.

So, for the leaf example, above we have

leaves_per_quadrant <- 1.1
n_quadrants         <- 100

expected_leaves <- tibble(n_leaves = 0:6, 
       prob_n_leaves = dpois(x = n_leaves, lambda = leaves_per_quadrant),
       expected_number_quadrats = n_quadrants * prob_n_leaves)
n_leaves prob_n_leaves expected_number_quadrats
0 0.3328711 33.2871084
1 0.3661582 36.6158192
2 0.2013870 20.1387006
3 0.0738419 7.3841902
4 0.0203065 2.0306523
5 0.0044674 0.4467435
6 0.0008190 0.0819030 
location_histogram +
  geom_line(data = expected_leaves, aes(x = n_leaves , y = expected_number_quadrats), color = "red")+
  annotate(x = 4, y = 30, geom = "text", label = "Poisson\nexpectations", color = "red", hjust = 0)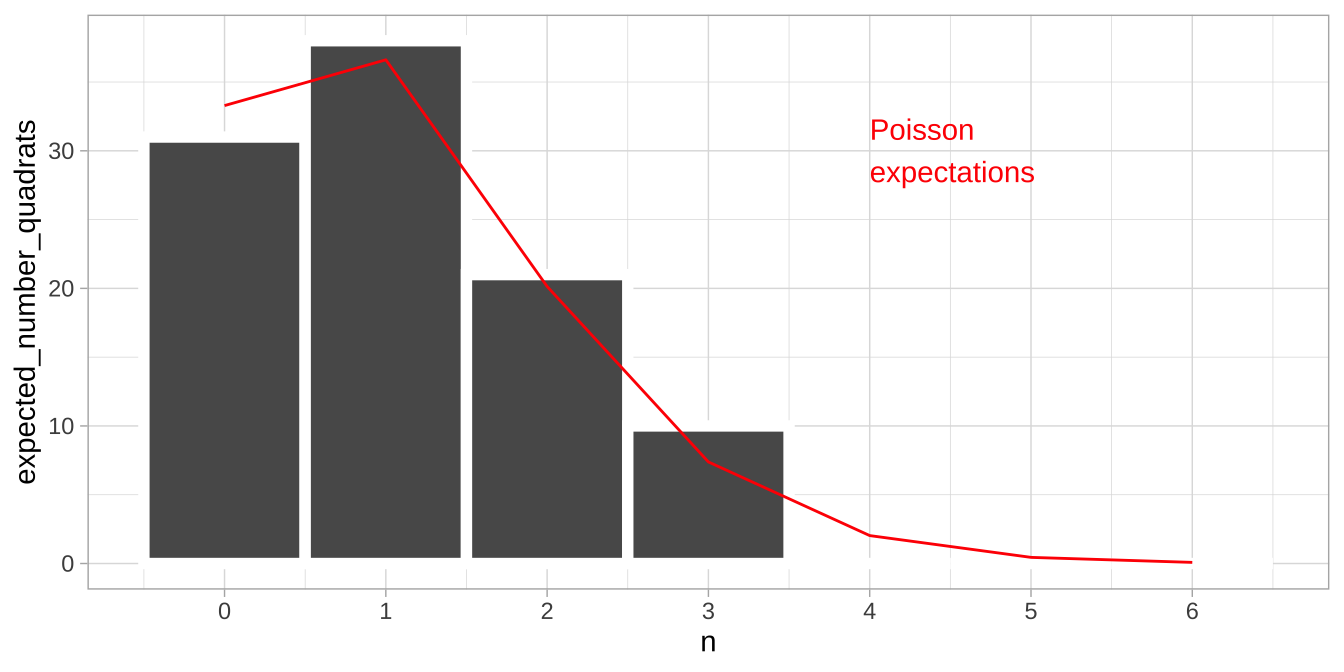

The Poisson regression

The poison regression is a generalized linear model for Poisson distributed data. As in the logistic regression, the linear predictor is the familiar regression equation:

\[\widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times y_{2,i} + \dots\]

\(\widehat{Y_i}\) is not our prediction for the count \(\widehat{\lambda_i}\). Rather, in a GLM, we use this “linear predictor” through the “link function” to find our prediction.

For a Poisson regression, the “linear predictor” describes the log of the predicted number, which we can convert to the predicted count by exponentiation. That is,

\[\widehat{\lambda_i} = e^{Y_i}\]
So if our link function says that the log of the expected count, \(\widehat{Y_i}\), equals 3, we expect, on average, a count of \(e^{3} = 20\). We can find this in R as

Poisson regression example: Elephent

Do older elephant males have more mates?

elephants <- tibble(mates = c(0,1,1,1,3,0,0,0,2,2,2,1,2,4,3,3, 3,2,1,1,2,3,5,6,1, 1,6,2,1,3,4,0,2,3,4,9,3,5,7,2,9), 
                    age = c(27,28,28,28,28,29,29,29,29,29,29,30,32,33,33,33, 33,33,34,34, 34,34,36,36,37,37,37,38,39,41,42,43, 43,43,43,43,44,45,47,48,52))

(Imperfect) Option 1: Linear model on raw data

ggplot(elephants, aes(x = age, y = mates, label = emoji("elephant"))) +
  geom_text(family="EmojiOne", color = "black",
            position = position_jitter(width = .1, height = .1))+
  geom_smooth(method = "lm")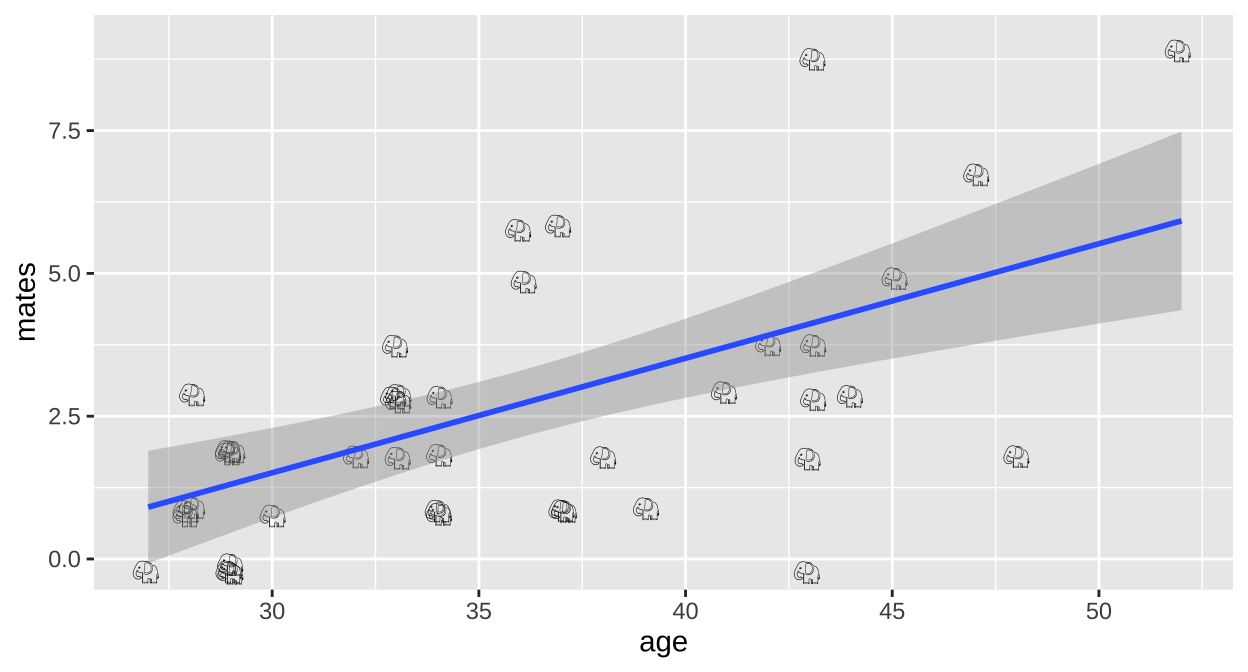

We could simply run a linear regression.

elephant_lm1 <- lm(mates ~ age, data = elephants)
summary(elephant_lm1)

Call:
lm(formula = mates ~ age, data = elephants)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.1158 -1.3087 -0.1082  0.8892  4.8842 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -4.50589    1.61899  -2.783  0.00826 ** 
age          0.20050    0.04443   4.513 5.75e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.849 on 39 degrees of freedom
Multiple R-squared:  0.343, Adjusted R-squared:  0.3262 
F-statistic: 20.36 on 1 and 39 DF,  p-value: 5.749e-05

Here we estimate that elephant males expect, on avaerage, an additional 0.20 mates (95% CI 0.11, 0.29) for every year they live.

But we can see a few issues in the diagnostic plots – namely, the “scale-location” plot shows that the variance in the residuals increases with the predicted value.

autoplot(elephant_lm1, ncol = 4)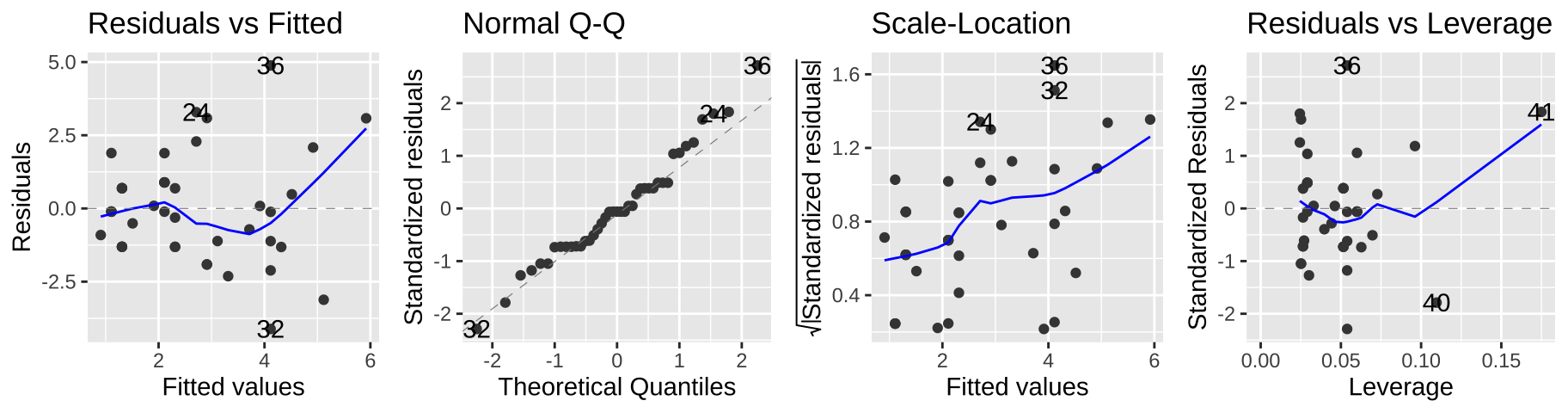

(Imperfect) Option 2: Linear model on log plus one transformed data

ggplot(elephants, aes(x = age, y = mates, label = emoji("elephant"))) +
  geom_text(family="EmojiOne", color = "black",
            position = position_jitter(width = .1, height = .1))+
  geom_smooth(method = "lm")+
  scale_y_continuous(trans = "log1p")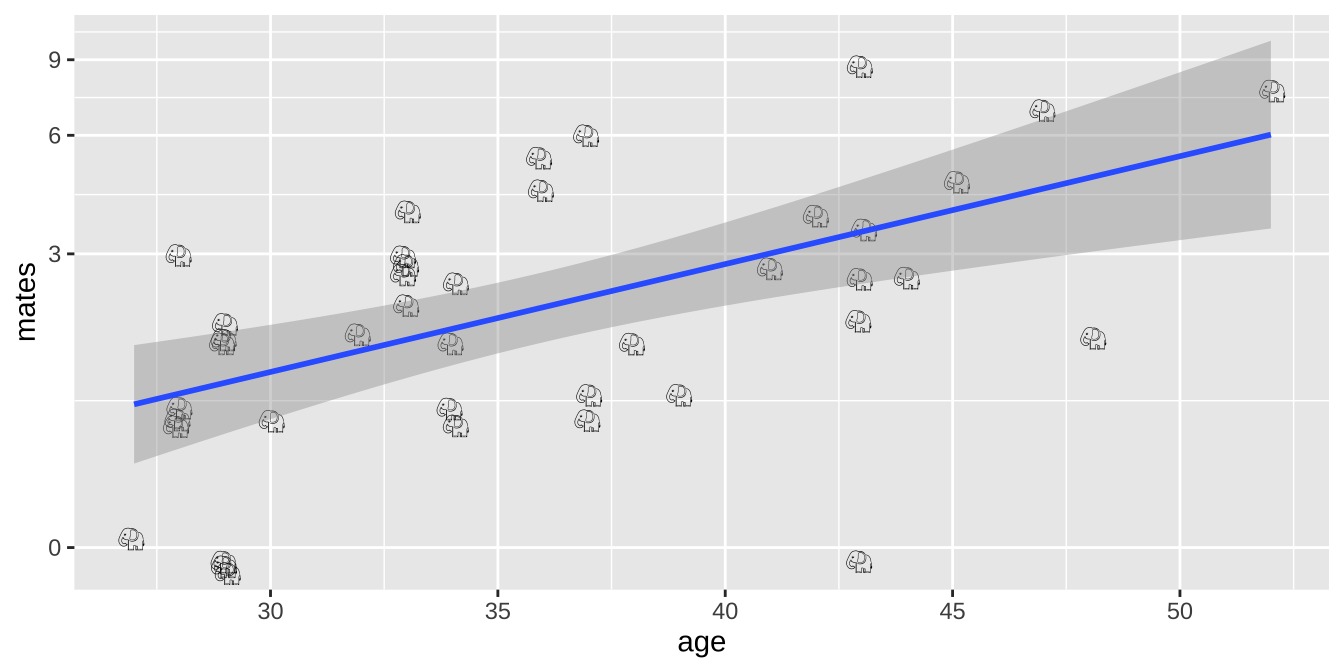

Alternatively, we could add one to the number of maters and then log transfoarm to better meet assumptions of the linear model

elephant_lm2 <- lm(log1p(mates) ~ age, data = elephants)
summary(elephant_lm2)

Call:
lm(formula = log1p(mates) ~ age, data = elephants)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.49087 -0.33939  0.06607  0.35376  0.81171 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.69893    0.45861  -1.524 0.135567    
age          0.05093    0.01259   4.046 0.000238 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5237 on 39 degrees of freedom
Multiple R-squared:  0.2957,    Adjusted R-squared:  0.2776 
F-statistic: 16.37 on 1 and 39 DF,  p-value: 0.0002385

These model parameters take a minute to interpret – we start with an intercept of -0.69893 and add 0.05093 for each year lived. To turn this into a prediction, we exponentiate ad subtract one. So, for example, we predict that a 40 year old elephant will have \(e^{(-0.69893 + 40 \times 0.05093)}-1 = 2.81\) mates.

autoplot(elephant_lm2, ncol = 4)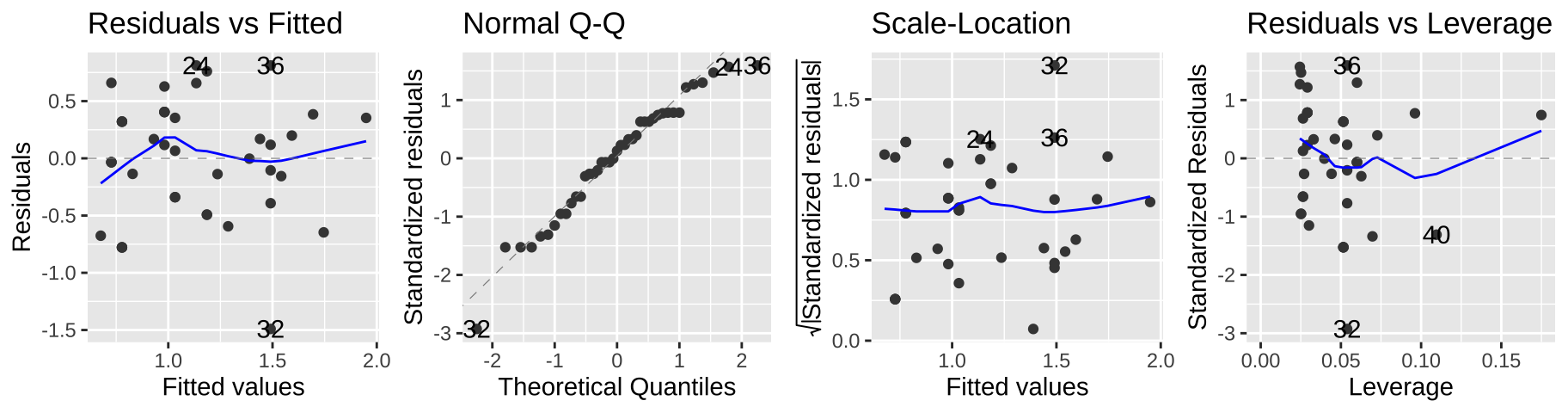

This seems to meet model assumptions pretty well, and is a totally acceptable option – but in a sense, we already dealt with the complexity of transforming our data for the model and then back-transforming to explain the results, so a Poisson regression might be more convenient.

(Better) Option 3: Poisson regression

Rather than transforming the data to fit the test, we can actually model the data we have. We do this with the Poisson Regression.

We model data as being Poisson distributed – that is, we ultimately predict the expected count for a given predictor \(\lambda_i\) assuming Poisson distributed errors. But remember that before that, we find our linear predictor, \(Y_i\), as we do for a standard linear model, and the exponential our prediction, \(Y_i\) to find \(\lambda_i\).

As with the logistic regression (above), we find the linear predictor with the glm() function. This time, we specify that we are modeling a Poisson random variable with a log link function:

elephant.glm <- glm(mates ~ age, data = elephants, family = poisson(link = "log"))
elephant.glm 

Call:  glm(formula = mates ~ age, family = poisson(link = "log"), data = elephants)

Coefficients:
(Intercept)          age  
   -1.58201      0.06869  

Degrees of Freedom: 40 Total (i.e. Null);  39 Residual
Null Deviance:      75.37 
Residual Deviance: 51.01    AIC: 156.5

Predictions from a poisson regression

So for our linear predictor, we begin with an intercept of -1.582 and add 0.06869 for every year an elephant has lived. So for a 40 year old elephant, the linear predictor, \(Y_{age = 40} = -1.582 + 40 \times 0.06869 = 1.1656\). Exponentiating this (to convert from log to linear scale), we predict that a 40 year old elephant male, will have, on average \(e^{1.1656} = 3.2\) mates (in R exp(1.1656)), with Poisson distributed error.

Plotting results of a poisson regression

We can visualize the poisson regression as follows:

ggplot(elephants, aes(x = age, y = mates, label = emoji("elephant"))) +
  geom_text(family="EmojiOne", color = "black",
            position = position_jitter(width = .1, height = .1))+
  geom_smooth(method = "glm",method.args = list('poisson'))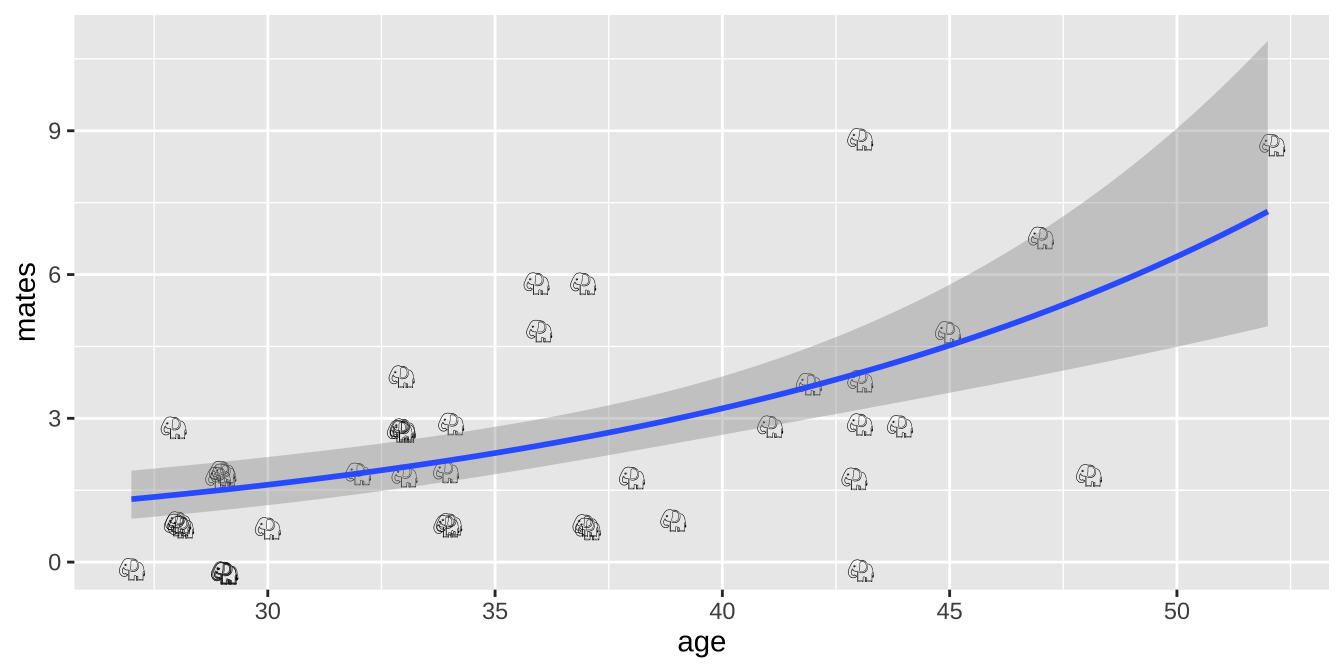

Hypothesis testing for a poisson regression

As with the logistic regression (Ch ??), we compare the likelihood of our MLE parameter estimate to a null model with a likelihood ratio test.

We can do this ourselves

null.elephant.glm <- glm(mates ~1, data = elephants, family = poisson(link = "log"))
D                 <- 2 * (logLik(elephant.glm) - logLik(null.elephant.glm))
p.val             <- pchisq(q = D, df = 1, lower.tail = FALSE)
c(D=D, p.val = p.val)
           D        p.val 
2.436011e+01 7.990620e-07

Or with the anova() function

anova(elephant.glm, test = "LRT")
Analysis of Deviance Table

Model: poisson, link: log

Response: mates

Terms added sequentially (first to last)

     Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                    40     75.372              
age   1    24.36        39     51.012 7.991e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We see that the “deviance” that R calculates is our D, and that our p-values match R’s.

We reject thee null!

An aside on the deviance

If we look at our GLM output, wee see “Null Deviance” and “Reidual Deviance”, with our D eaul to two times their difference.

elephant.glm

Call:  glm(formula = mates ~ age, family = poisson(link = "log"), data = elephants)

Coefficients:
(Intercept)          age  
   -1.58201      0.06869  

Degrees of Freedom: 40 Total (i.e. Null);  39 Residual
Null Deviance:      75.37 
Residual Deviance: 51.01    AIC: 156.5

What does this mean?

Well, we first find the log likelihood likelihood of the perfect, “oversaturated” model, for which every prediction is perfect.

oversaturated_elephants <- elephants %>%
  dplyr::select(mates) %>%
  mutate(logLik = dpois(x = mates, lambda = mates, log = TRUE))

So the log likelihood of a perfect model is summarise(oversaturated_elephants, logLik = sum(logLik)) = -50.7230814.

We find the log likelihood of our model is

logLik_elephant_glm <- broom::augment(elephant.glm) %>%
   dplyr::select(mates,   age, .fitted)%>% 
    mutate(lambda = exp(.fitted),
           logLik = dpois(x = mates, lambda = lambda, log = TRUE))
DT::datatable(logLik_elephant_glm %>%
                mutate(.fitted = round(.fitted,digits = 3),
                       lambda = round(lambda, digits = 3),
                       logLik = round(logLik, digits =3)), 
              options = list(autoWidth = TRUE,pageLength = 5, lengthMenu = c(5, 25, 50)))

So the log likelihood of our model is summarise(logLik_elephant_glm, logLik = sum(logLik)) = -76.2288953, which is what we could have found by logLik(elephant.glm) = -76.2288953.

The “Residual Deviance” is two times the difference in the log likelihood of a perfect model, -50.72308 and our model, -76.2289 – i.e. 2 * ((-50.72308 ) - (-76.2289 )) = 51.01164.

We can then get our “Deviance” of 75.37174 - 51.01164 = 24.3601, which we previously found by simply taking two times the difference in the log likelihood of the MLE and null models.

An aside on residuals

If we look at the residuals of our model, we see something strange…

broom::augment(elephant.glm)

It is not the difference between our observation, mates and \(\widehat{Y_i}\), nor is it the difference between our prediction and the predicted \(\lambda_i\) (for example we have zero mates and a prediction of $e^{0.273} = 1.3139. The acutal calculation is a bit obscure, and we won’t adress it here, just know that they should look good on a diagnostic plot, and if they don’t, there may be better options that a Poisson regression.

See this for more background on interpretting residuals from poisson regression.

Assumptions of poisson regression

Remember that a GLM still makes assumptions and that these assumptions can differ from the of a linear model because we are building a different model.

A poisson regression assumes that

Viewing our standard diagnostic plots can help us evaluate some of these assumptions. As I said above, don’t think too hard about these y-values – think of them as a residual that would look as we hpoe if the model was a good fit.

autoplot(elephant.glm, ncol=4)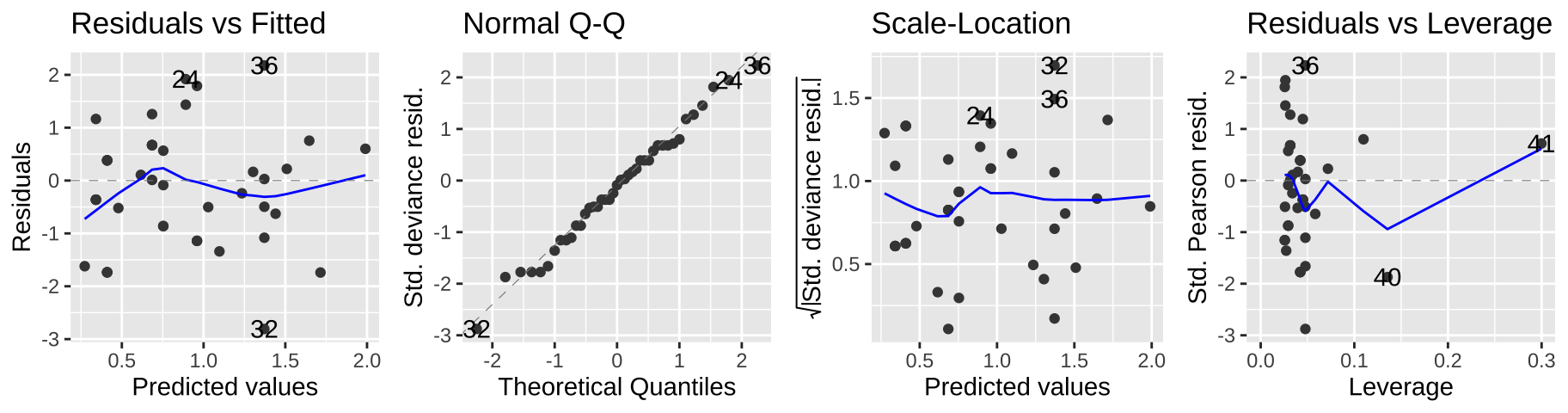

Another rough diagnostic is to look at the “Dispersion” – a measure of how much more variance we see than we expect from a Poisson model. We can approximate this by dividing the Residual deviance by the degrees of freedom.

In our case this is 51.01/40 = 1.275, which is just fine.

Model fit

We can also evaluate if the model is a reasonable description of the data by comparing our likelihoods to the likelihood of data simulated directly from the model.

Let’s make this concretre by simulating once with the rpois() function:

sim1 <- broom::augment(elephant.glm) %>%
  dplyr::select(mates,   age, .fitted) %>%
  mutate(simulated = rpois(n=n(), lambda = exp(.fitted)),
         logLikSim = dpois(x = simulated, lambda = exp(.fitted), log = TRUE))

So the log likelihood of this data set simulaed from our mode is sim1 %>% summarise(sum(logLikSim)) = -72.803015. Which isn’t far from the likelihood of the the model for the actual data– logLik(elephant.glm) -76.2288953.

If we did a bunch of these simulations and our log likelihood way further from zero than nearly all simulated cases, we’d worry about model fit. The histogram below suggests

# here we write a function to simulate data from a poisson with predictions of a linear model 
# and return the log likelihood

simPois <- function(pois.glm){
  broom::augment(pois.glm) %>%
    dplyr::select(.fitted) %>%
    mutate(simulated = rpois(n=n(), lambda = exp(.fitted)),
           logLikSim = dpois(x = simulated, lambda = exp(.fitted), log = TRUE)) %>%
    summarise(loglik = sum(logLikSim)) %>% 
    pull()
}


tibble(simLogLiks = replicate(n = 1000, simPois(pois.glm = elephant.glm))) %>% # simulate 1000 times
  ggplot(aes(x = simLogLiks)) +
  geom_histogram(bins = 30)+
  scale_x_reverse()+
  geom_vline(xintercept =  logLik(elephant.glm), color = "red")+ 
  labs(subtitle = "Comparing the log likelihood with real and simulated data")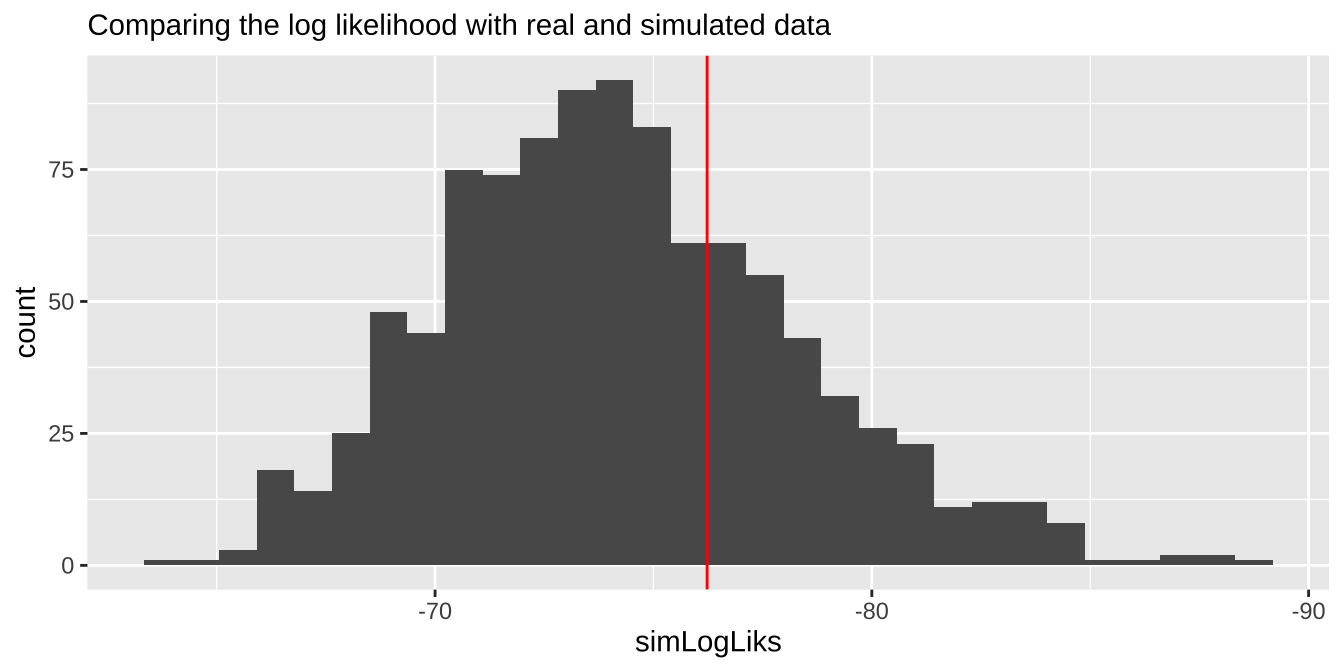

Alternatives to the poisson regresssion

So, the Poisson is a good model if count data are random over space or time. But sometimes they are not. Common violations of Poisson assumptions include

Quasipoisson & beta-binomial are usually good options for modeling overdispersion.

“Hurdle” models can be used to model “zero inflated” data.

Quiz

Figure 1: Quiz on generalized linear models here

Advanced / under the hood.

How did we find the maximum likelihood?

A straightforward but computationally intense way is a grid search. Here we look over a bunch of parameter combinations and then find the one with the largest log likelihood. R uses more efficient methods to basically do the same thing.

Here’s how we can do this

  1. Propose a bunch of plausible parameter values (aka models)
models <- crossing(intercept = seq(-2, 2, 0.025),
                   slope     = seq(-.5,.5, .01)) %>%
  mutate(model = 1:n())
  1. Evaluate the log-likelihood of each model given the data.
fishLogLik <- function(slope, intercept, dat){
    model_log_lik <- dat %>%
    mutate(p = plogis(intercept + slope * Time),
           logLik = dbinom(x = Alive, size = 1, prob = p, log = TRUE)) %>%
    summarise(sum(logLik)) %>%
    pull()
  return(model_log_lik)
}

models_logLiks <- models %>%
  nest(params = c(intercept, slope)) %>%
  mutate(log_lik = purrr::map_dbl(.x = params, ~ fishLogLik(slope = .x$slope,
                                                   intercept = .x$intercept, 
                                                   dat = cold.fish)))%>%
  unnest(cols = c(params))
  1. Find the MLE as the proposed parameters with the greatest log likelihood
top_n(models_logLiks, log_lik, n=1)                                                                                                    %>% kable()
model intercept slope log_lik
13866 1.425 -0.22 -82.35143

Reasuringly, this matches R’s answer.

  1. We can also use this output to plot a likelihood surface
ggplot(models_logLiks, aes(x = slope, y = intercept, fill = log_lik))+
  geom_tile()+
  scale_fill_gradientn(colours = terrain.colors(500))+ 
  geom_text(data = . %>% top_n(log_lik, n=1), aes(label = "* MLE"), 
            hjust = 0, color = "red")+ 
  theme_tufte()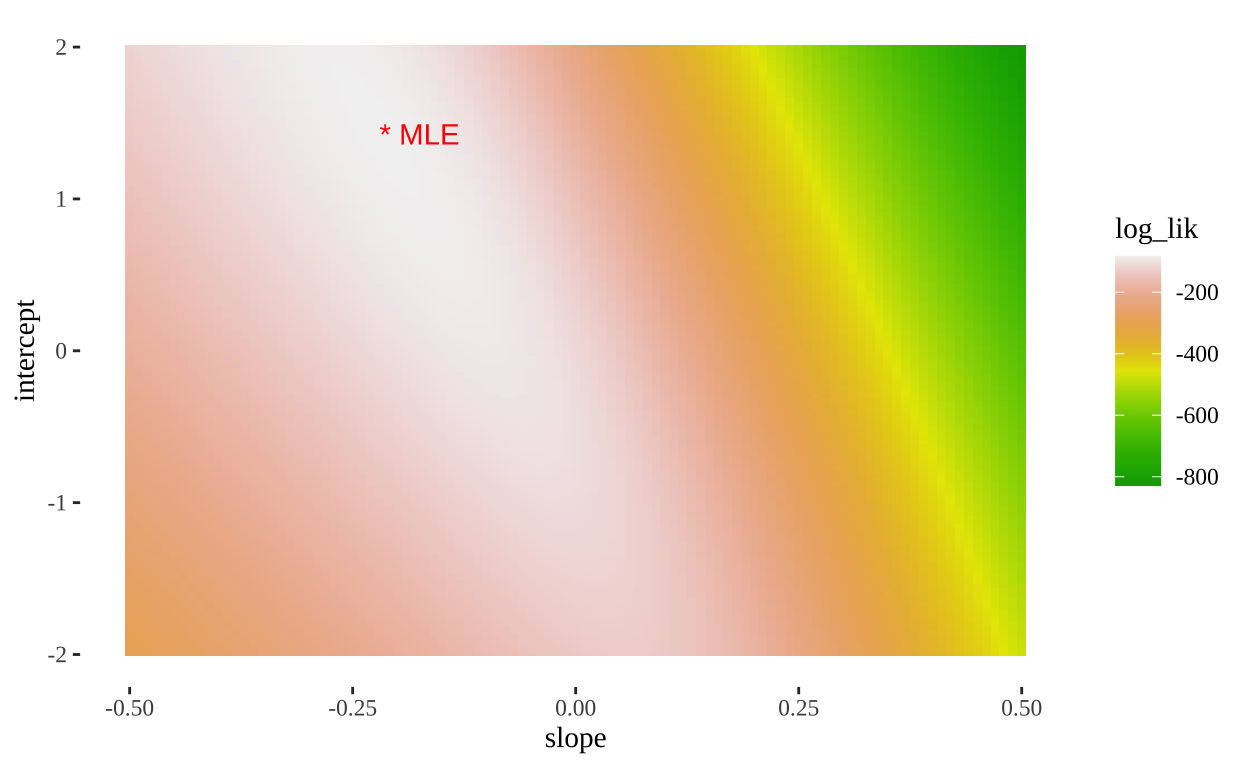

  1. Finally, we can compare the logLikihood of this model (our best) which equals -82.35143 to the one where we just take the overal mean proportion
cold.fish %>%
    mutate(logLik = dbinom(x = Alive, size = 1, 
                           prob =  summarise(cold.fish, mean(Alive)) %>% pull(),
                           log = TRUE)) %>%
    summarise(sum(logLik)) %>%
  pull()
[1] -104.7749

So D = 2* (-82.35143 - (-104.7749)) = 44.84694, and our p-value is pchisq(q = 44.84694, df = 1, lower.tail = FALSE) = 2.1305356^{-11}, which is basically our answer above, save minor rounding error!

References