Chapter 32: Likelihood

An introduction to likelihood based inference.

Motivating Scenario: We aim to make inferences on data from various types of null models.

Likelihood-Based Inference

So far, we’ve focused extensively on the normal distribution in our linear modeling. This makes sense: many things are approximately normal, but certainly not everything. We’ve also assumed independence — though this assumption is more tenuous, as true independence usually only holds in carefully controlled experiments.

The good news is that we can step beyond the assumptions of linear models and build inferences under any model we can describe through an equation using likelihood-based inference! This approach allows us to model more complex scenarios, like phylogenies, genome sequences, or any structured data. For now, however, we’ll stick to our simple normal distribution so that we can follow along.

Probabilities and Likelihoods

Remember, a probability represents the proportion of times a model would produce a particular result if we did the same thing many many times.

Mathematically, calculating a likelihood is identical to calculating a probability. The key difference lies in our perspective.

In this way, a likelihood represents a conditional probability.

\[P(\text{Data} | \text{Model}) = \mathscr{L}(\text{Model} | \text{Data})\]

Log-Likelihoods

If our data points are independent, we can calculate the likelihood of all data points by taking the product of each individual likelihood. However, this approach introduces some practical challenges:

To address these issues, we typically take the log of each likelihood and sum them all. In log space, addition replaces multiplication — for example, 0.5 * 0.2 = 0.1 becomes log(0.5) + log(0.2) = -2.302585, and \(e^{-2.302585} = 0.1\). So you will almost always see people talking about log-likelihoods instead of raw likelihoods.

Log Likelihood of \(\mu\)

How can we calculate likelihoods for a parameter of a normal distribution? Here’s how!

Suppose we have a sample with values 0.01, 0.07, and 2.2, and we know the population standard deviation is one, but we don’t know the population mean. We can find the likelihood of a proposed mean by multiplying the probability of each observation, given the proposed mean. For example, the likelihood of \(\mu = 0 | \sigma = 1, \text{ and } Data = \{0.01, 0.07, 2.2\}\) is:

dnorm(x = 0.01, mean = 0, sd = 1) * 
  dnorm(x = 0.07, mean = 0, sd = 1) * 
  dnorm(x = 2.20, mean = 0, sd = 1)
[1] 0.00563186

A more compact way to write this is

dnorm(x = c(0.01, 0.07, 2.20), mean = 0, sd = 1) %>% prod()
[1] 0.00563186

Remember, we multiply because we assume that all observations are independent.

As discussed above, we typically work with log likelihoods rather than linear likelihoods. Because multiplying on the linear scale is equivalent to adding on the log scale, the log likelihood in this case is:

dnorm(x = c(0.01, 0.07, 2.20), mean = 0, sd = 1, log = TRUE) %>% sum()
[1] -5.179316

Reassuringly, \(ln(0.00563186) =\) -5.1793155, and similarly \(e^{5.179316} =\) 0.0056319

The Likelihood Profile

We can consider a range of plausible parameter values and calculate the (log) likelihood of the data for each of these “models.” This is called a likelihood profile. We can create a likelihood profile with the following:

obs            <- c(0.01, 0.07, 2.2)    # our observations
proposed.means <- seq(-1, 2, .001)      # proposing means from -1 to 2 in 0.001 increments

likelihood_profile <- tibble(proposed_mean = proposed.means)%>%
  group_by(proposed_mean)%>%
  # find the logliklihood of each proposed "model"
  mutate(log_lik = sum(dnorm(x = obs, mean = proposed_mean , sd = 1, log = TRUE)))%>%
  ungroup()

Now you can scroll trrough and see the log likelihoods of each proposed mean

Above I just said the santdard deviation was one. But more often we find it rom our data. however

The stadard deviation in our likelihood calcualtions is a bit differet than we are used to.

  • First, we consider our sums of squares as deviations away from the proposed mean, rather than the estimated mean.
  • Second we divide by n, not not n-1 (because we state the mean and do not estimate it)

Maximum Likelihood Estimate

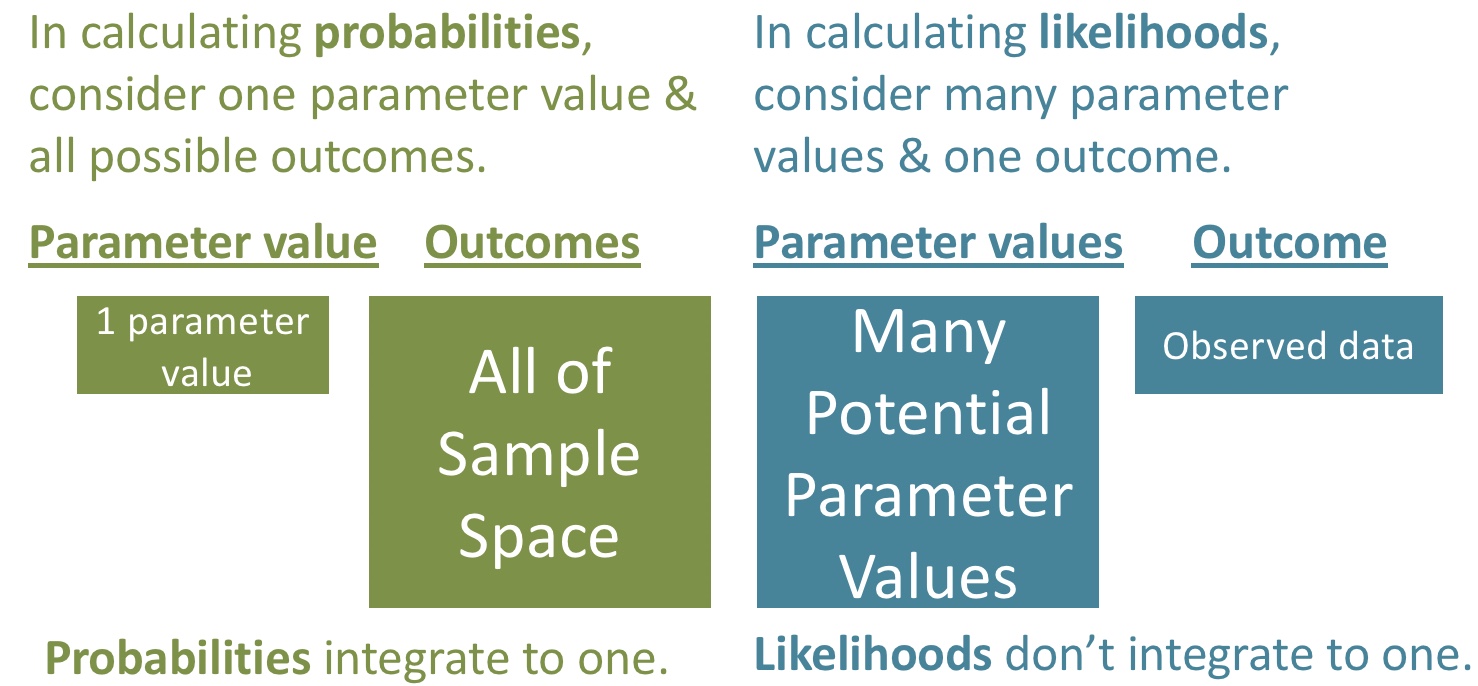
How can we use this for inference? One estimate of our parameter is the value that “maximizes the likelihood” of our data (e.g., the x-value corresponding to the highest point on the plot above).

To find the maximum likelihood estimate, we find the biggest value (i.e. the smallest negative number) in our likelihood profile. We can find this by arranging our data set from largest to smallest number

likelihood_profile%>% 
  arrange(desc(log_lik))

Or by filtering our data so we only have the proposed mean that maximizes the liklihood of our data

MLE <- likelihood_profile %>%
  filter(log_lik == max(log_lik))
print(MLE)
# A tibble: 1 × 2
  proposed_mean log_lik
          <dbl>   <dbl>
1          0.76   -4.31

This equals the mean of our observations: mean(c(0.01, 0.07, 2.2)) = 0.76. In general, for normally distributed data, the maximum likelihood estimate of the population mean is the sample mean.

NOTE The maximium liklihood estimate is not the parameter with the best chance of being correct (that’s a Bayesian question); rather, it’s the parameter that, if true, would have the greatest likelihood of producing our observed data.

Likelihood based inference: Uncertainty and hypothesis testing.

Uncertainty

We need one more trick to use the likelihood profile to estimate uncertainty – log likelihoods are roughly \(\chi^2\) distributed with degrees of freedom equal to the number of parameters we’re trying to guess (here, just one – corresponding to the mean). So for 95% confidence intervals are everything within qchisq(p = .95, df =1) /2 = 1.92 log likelihood units of the maximum likelihood estimate.

in95CI <- pull(MLE, log_lik) -1.92

CI <- likelihood_profile %>%
  filter(log_lik > in95CI) %>%
  reframe(CI = range(proposed_mean))
CI
-0.371
1.891

Now we can plot our likelihood profile, noting our MLE (in red) and 95% confidence intervals (the shaded area):

ggplot(likelihood_profile)+
  geom_rect(data = .  %>% summarise(ymin = min(log_lik),ymax = max(log_lik),
                                 xmin = min(pull(CI )),xmax = max(pull(CI ))),
            aes(xmin = xmin,xmax = xmax, ymin = ymin, ymax = ymax), 
            fill= "lightgrey", alpha = .4)+
  geom_line(aes(x = proposed_mean, y = log_lik))+
  geom_vline(xintercept = pull(MLE, proposed_mean), color = "red")+
  theme_light()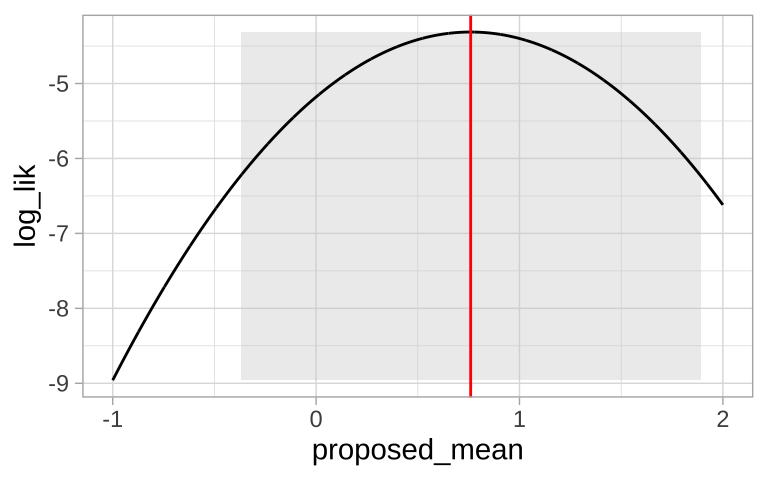

Null hypothesis significance testing.

We can find a p-value and test the null hypothesis by comparing the likelihood of our MLE (\(log\mathscr{L}(MLE|D)\)) to the likelihood of the null model (\(log\mathscr{L}(H_0|D)\)). We call this a likelihood ratio test, because we divide the likelihood of the MLE by the likelihood of the null – but we’re doing this in logs, so we subtract rather than divide. For this arbitrary example, lets pretent we want to test the null that the true mean is zero:

We then calculate \(D\) which is simply two times this difference in lof likelihoods, and calculate a p-value with it by noting that \(D\) is \(\chi^2\) distributed with degrees of freedom equal to the number of parameters we’re inferring (here, just one – corresponding to the mean). We see that our p value is greater than 0.05 so we fail to reject the null.

log_lik_MLE <- pull(MLE, log_lik)
log_lik_H0  <- likelihood_profile %>% filter(proposed_mean == 0)%>% pull(log_lik)
D      <- 2 * (log_lik_MLE - log_lik_H0)
p_val  <- pchisq(q = D, df = 1, lower.tail = FALSE)
D p_val
1.733 0.188

Unfortunately, the LRT test give poorly calibrated p-values – especially when we have a small sample size.

Compare our LRT pvalue of 0.188 to thats from a one sample t-test

t.test(obs,mu=0) %>%tidy() %>% pull(p.value)
[1] 0.401964

A simple solution is applying Bartlett’s Correction for Small Samples correction, here \(D_\text{corrected} = \frac{D}{1+\frac{1}{2\times n}}\). This gets us closer, but we still must recognize that the LRT is a very rough approximtation

Bartlett_D      <- D / (1+1/(2 * length(obs)))
Bartlett_p_val  <- pchisq(q = Bartlett_D, df = 1, lower.tail = FALSE)
print(Bartlett_p_val)
[1] 0.2229538

Example 1: Are species moving uphill?

Chen et al. (2011) tested the idea that organisms move to higher elevation as the climate warms. To test this, they collected data (available here) from 31 species, plotted below (Fig 1).

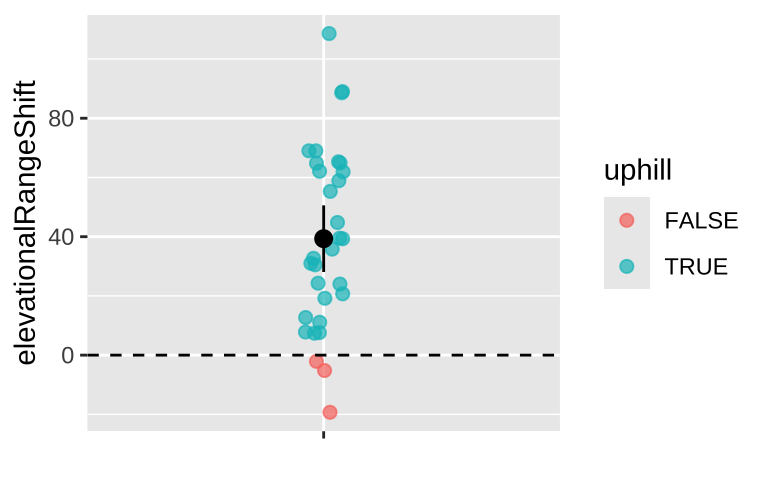
Change in the elevation of 31 species. Data from @Chen2011.

Figure 1: Change in the elevation of 31 species. Data from Chen et al. (2011).

We could conduct a one sample t-test against of the null hypothesis that there has been zero net change on average.

lm(elevationalRangeShift ~ 1, data = range_shift) %>%
  tidy()                                                                                                                                                                           %>% mutate(p.value = p.value* 10^8)%>%mutate_at(2:5, round, digits = 2) %>% mutate(p.value = paste(p.value,"x 10^-8"))%>% gt()
term estimate std.error statistic p.value
(Intercept) 39.33 5.51 7.14 6.06 x 10^-8

Calculate log likelihoods for each model

There is nothing wrong with that one-sample t-test, but let’s use this as an opportunity to learn about how to apply likelihood. First we grab our observations, write down our proposed means – lets say from negative one hundred to two hundred in increments of .01.

observations   <-  pull(range_shift, elevationalRangeShift)
proposed_means <- seq(-100,200,.01)
n               <- length(observations)

We then go on to make a likelihood surface by.

  1. Making a vector of proposed means

  2. Calculate the population standard deviation (sigma) for each proposed parameter value,

  3. For each proposed mean, find the log likelihood of each observation (with dnorm)

  4. Sum the log likelihoods of each observation for a given proposed mean to find the log likelihood of that parameter estimate given the data.

Just for fun well arrange them with the MLE on top!

log_lik_uphill <- tibble(mu = proposed_means)%>%      # Step 1 
  group_by(mu)%>%                                        # R stuff to make sure we only work within a parameter
  mutate(sigma   = sqrt(sum((observations-mu)^2) / n) ,  # Step 2: Find the standard deviation  
         log_lik = dnorm(x = observations,               # Step 3: Find the 
                         mean = mu,                      #    log-likelihood
                         sd = sigma,                     #    if each data 
                         log= TRUE)%>%                   #    point
           sum())%>%                                     # Step 4: Sum the log-liklihoods
  ungroup()%>%
  arrange(desc(log_lik))

Figure 2: Log likelihoods of for 100 proposed means (a subst of those investigated above), sorted from highest to lowest log likelihood.

MLE

This sorted list shows that our maximum likelihood estimate is about 39 meters. The actual MLE is about

MLE <- log_lik_uphill %>%
  filter(log_lik == max(log_lik))
mu sigma log_lik
39.3 30.2 -149.6

95% CI

Again, because log likelihoods are roughly \(\chi^2\) distributed with one degree of freedom, everything within qchisq(p = .95, df =1) /2 = 1.92 log likelihood units of the maximum likelihood estimate is in the 95% confidence interval:

in95CI <- pull(MLE, log_lik) -1.92

CI <- log_lik_uphill  %>%
  filter(log_lik > in95CI) %>%
  reframe(CI = range(mu))
CI
28.38
50.28

Now we can plot our likelihood profile, noting our MLE (in red) and 95% confidence intervals (the shaded area):

ggplot(log_lik_uphill)+
  geom_rect(data = .  %>% summarise(ymin = min(log_lik),ymax = max(log_lik),
                                 xmin = min(pull(CI )),xmax = max(pull(CI ))),
            aes(xmin = xmin,xmax = xmax, ymin = ymin, ymax = ymax), 
            fill= "lightgrey", alpha = .4)+
  geom_line(aes(x = mu, y = log_lik))+
  geom_vline(xintercept = pull(MLE, mu), color = "red")+
  theme_light()

Null hypothesis significance testing.

As above we find the p-value by comparing two times the difference in log likelihoods under the MLE and the null model (\(D\)), to the \(\chi^2\) distribution with one degress of freedom. This value is in the same ballpart as what we got from the one sample t-test (\(6.06 \times 10^{-8}\))

log_lik_MLE <- pull(MLE, log_lik)
log_lik_H0  <- log_lik_uphill %>% filter(mu == 0)%>% pull(log_lik)
D      <- 2 * (log_lik_MLE - log_lik_H0)
p_val  <- pchisq(q = D, df = 1, lower.tail = FALSE)
log_lik_MLE log_lik_H0 D p_val
-149.59 -164.99 30.79 2.87 x 10^-8

R tricks

You can grag the log likelihoods of a model with the logLikfunction.

MLE_model <- lm(elevationalRangeShift ~ 1, data = range_shift) # Estimate the intercept
logLik(MLE_model ) %>% as.numeric()
[1] -149.5937
Null_model <- lm(elevationalRangeShift ~ 0, data = range_shift) # Set intercept to zero
logLik(Null_model ) %>% as.numeric()
[1] -164.9888

Or with the glance() function from broom

library(broom)
glance(MLE_model) %>% select(logLik) %>% pull()
[1] -149.5937

You can also use the lrtest function in the lmtest package to conduct this test:

library(lmtest)
lrtest(Null_model,MLE_model )
Likelihood ratio test

Model 1: elevationalRangeShift ~ 0
Model 2: elevationalRangeShift ~ 1
  #Df  LogLik Df Chisq Pr(>Chisq)    
1   1 -164.99                        
2   2 -149.59  1 30.79  2.875e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Bayesian inference

We often care about how probable our model is given the data, rather than the reverse. Likelihoods can help us approach this! Remember Bayes’ theorem:

\[ P(Model|Data) = \frac{P(Data|Model) \times P(Model)}{P(Data)} \]

Taking this apart:

Today, we’ll assign an arbitrary prior probability for demonstration purposes. This is not ideal—Bayesian inferences are only meaningful to the extent that we can meaningfully interpret the posterior, which depends on having a well-justified prior. However, for the sake of this example, let’s assume a prior: the parameter is normally distributed with a mean of 0 and a standard deviation of 30.

bayes_uphill <- log_lik_uphill %>%
  mutate(lik   = exp(log_lik),
         prior = dnorm(x = mu, mean = 0, sd = 30) / sum(dnorm(x = mu, mean = 0, sd = 30) ),
         evidence  = sum(lik * prior),
         posterior =  (lik *  prior) / evidence)

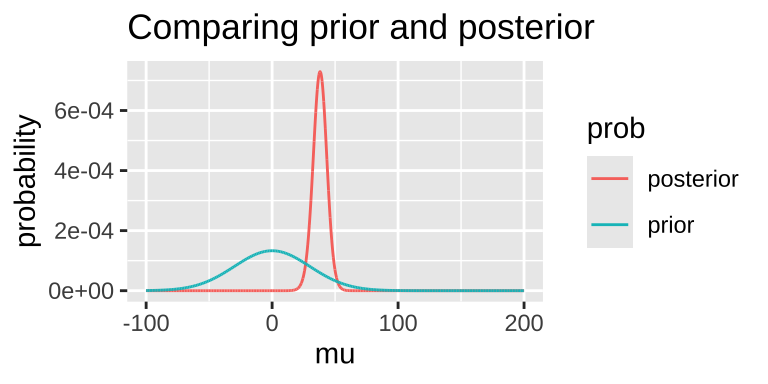
We can grab interesting thing from the posterior distribution.

bayes_uphill %>%
  filter(posterior == max(posterior))                                                                                                  %>% data.frame()
     mu    sigma   log_lik          lik        prior     evidence
1 38.08 30.19035 -149.6203 1.048907e-65 5.944371e-05 8.550126e-67
     posterior
1 0.0007292396

Note that this MAP estimate does not equal our MLE as it is pulled away from it by our prior.

bayes_uphill %>%
  mutate(cumProb = cumsum(posterior)) %>%
  filter(cumProb > 0.025 & cumProb < 0.975)%>%
  summarise(lower_95cred = min(mu),
            upper_95cred = max(mu))                                                                                                %>% data.frame()
  lower_95cred upper_95cred
1        26.18        52.48

Prior sensitivity

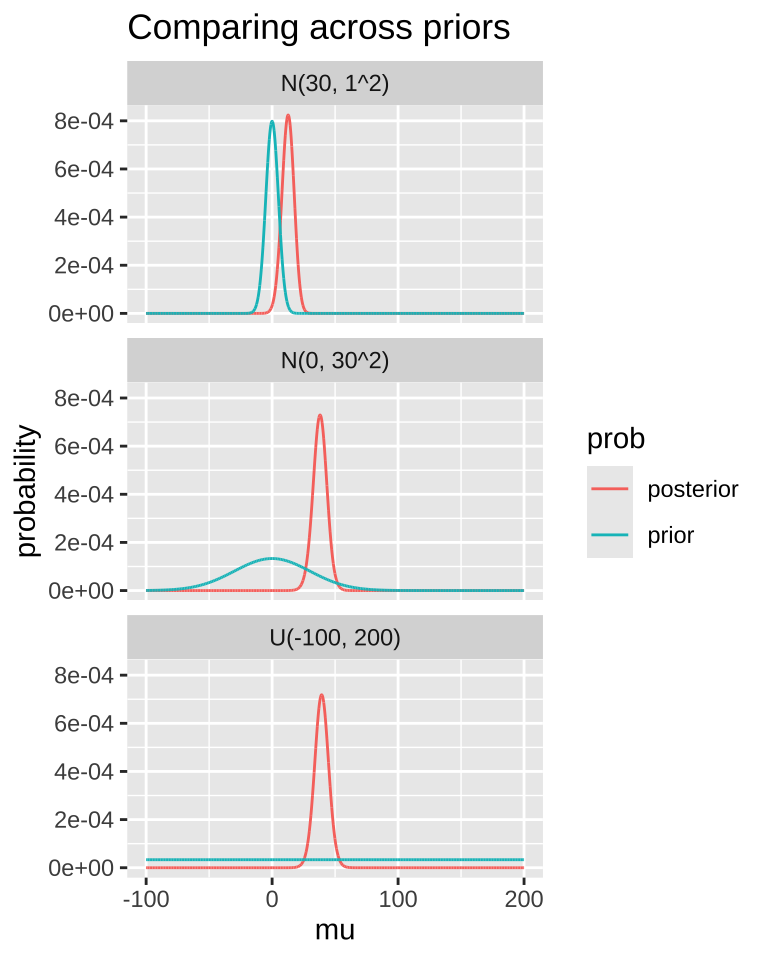
In a good world our priors are well calibrated.
In a better world, the evidence in the data is so strong, that our priors don’t matter.

A good thing to do is to compare our posterior distributions across different prior models. The plot below shows that if our prior is very tight, we have trouble moving the posterior away from it. Another way to say this, is that if your prior believe is strong, it would take loads of evidence to gr you to change it.

MCMC / STAN / brms

With more complex models, we usually can’t use the math above to solve Bayesian problems. Rather we use computer ticks – most notably the Markov Chain Monte Carlo MCMC to approximate the posterior distribution.

The programming here can be tedious so there are many programs – notable WINBUGS, JAGS and STAN – that make the computation easier. But even those can be a lot of work. Here I use the R package brms, which runs stan for us, to do an MCMC and do Bayesian stats. I suggest looking into this if you want to get stared, and learning STAN for more serious analyses

library(brms)
change.fit <- brm(elevationalRangeShift ~ 1, 
  data   = range_shift,
  family = gaussian(),
  prior  = set_prior("normal(0, 30)", 
                      class = "Intercept"),
  chains = 4,
  iter   = 5000)

change.fit$fit
term mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
b_Intercept 37.82 0.06 5.69 26.56 34.11 37.86 41.59 48.82 7863 1
sigma 31.70 0.05 4.25 24.84 28.68 31.24 34.20 41.34 6444 1
lp__ -156.70 0.02 1.04 -159.48 -157.09 -156.38 -155.97 -155.70 4340 1

Figure 3: Quiz on likelihood-based inference here

Chen, I-Ching, Jane K. Hill, Ralf Ohlemüller, David B. Roy, and Chris D. Thomas. 2011. “Rapid Range Shifts of Species Associated with High Levels of Climate Warming.” Science 333 (6045): 1024–26. https://doi.org/10.1126/science.1206432.

References