Chapter 21: Normal

The normal distribution.

Motivating Scenarios: We want to understand what’s so special about the normal distribution — what are its properties? Why do we see it so often? Why do we use it so frequently? What makes it so useful?

Learning Goals: By the end of this chapter, you should be able to:

• Describe the properties of a normal distribution.
  
• Understand that the standard error of the sampling distribution for a sample size n from a normal distribution equals \(\frac{\sigma}{\sqrt{n}}\).
  
• Find the probability density of a (range of) sample mean(s).
  
• Use a Z-transform to convert any normal distribution into the standard normal distribution.
  
• Interpret histograms and QQ-plots to evaluate whether data are roughly normal.
  
• Explain why normal distributions are common, and describe the Central Limit Theorem.
  
• Transform non-normal data to become approximately normal.
  
• Use the _norm() family of functions to:
  • Simulate random numbers from a normal distribution using rnorm().
    
  • Calculate the probability density of an observation from a specified normal distribution using dnorm().
    
  • Calculate the probability of observing a value more extreme than a number of interest in a specified normal distribution using pnorm().
    
  • Find a specified quantile of a normal distribution using qnorm().

Probability Densities for Continuous Variables

Unlike discrete distributions, where we can list every possible outcome (e.g., zero success, one success, etc., up to n successes) and sum their probabilities to one (i.e., \(\sum p_x=1\)), the probability of any single outcome from a continuous distribution, such as the normal distribution, is infinitesimally small because there are infinite numbers within any range. Thus, we describe continuous distributions using probability densities. Probability densities integrate to one (i.e., \(\int p_x=1\)), and can even exceed one at some points. (See Fig 1)

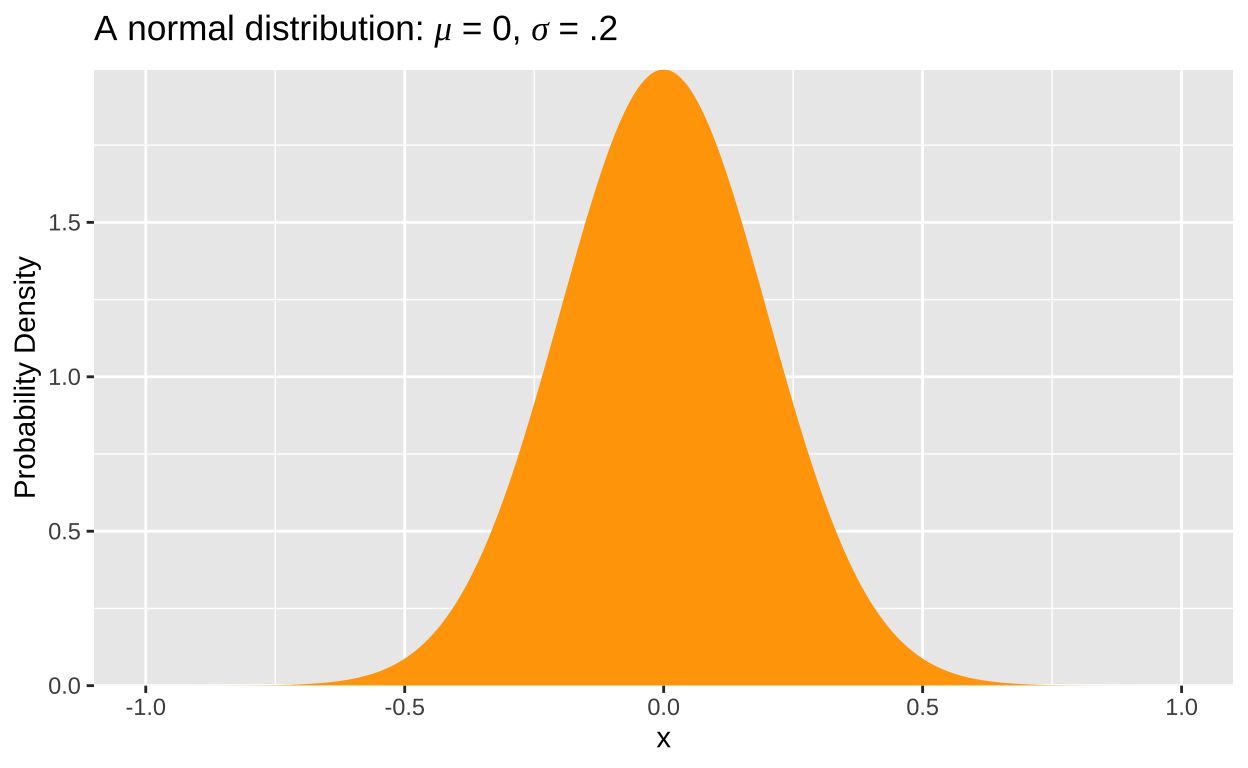
Figure 1: A normal distribution with a mean, μ, of zero, and standard deviation, σ, of 0.2.

The many normal distributions

Each normal distribution is fully characterized by two parameters: the mean \(\mu\) and the variance \(\sigma^2\) (or the standard deviation, \(\sigma\)). To the right, I show four different normal distributions, illustrating all combinations of \(\mu = 0\) or \(\mu = 5\) and \(\sigma = 2\) or \(\sigma = 0.2\).

The probability density for each value on the x-axis is given by the formula:

\[\begin{equation} f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}} \tag{1} \end{equation}\]

We efficiently describe a normally distributed random variable as \(X \sim N(\mu, \sigma^2)\), where \(\sim\) means is distributed as. For example, \(X\) is normally distributed with mean \(\mu\) and variance \(\sigma^2\). So, the mathematical notation for a variable \(X\) being normally distributed with a mean of \(\mu = 0.5\) and variance \(\sigma^2 = 0.1^2\) is \(X \sim N(0.5, 0.01)\).

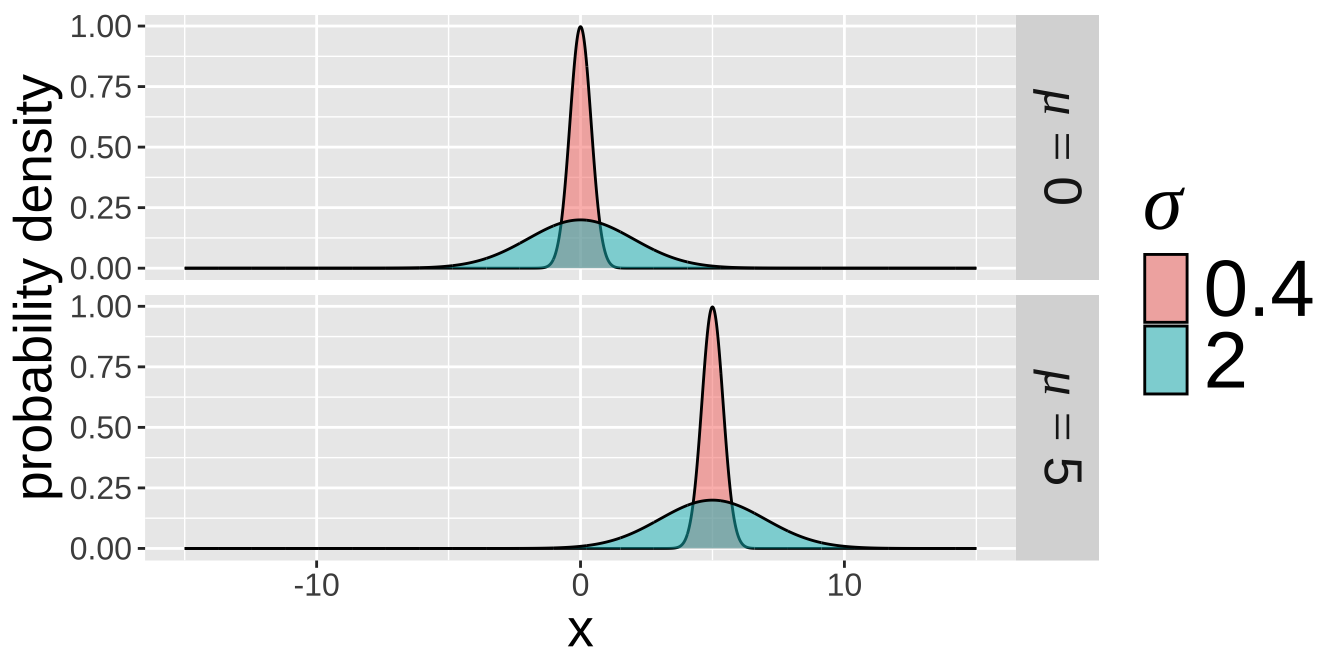
Figure 2: Four potential normal distributions. The top panel shows two normal distributions, both with a mean of zero. The distribution in red has a standard deviation of 0.4, while the blue distribution has a standard deviation of 2. In the lower panel, both normal distributions have a mean of 5, with standard deviations of 0.4 and 2.0 for the red and blue distributions, respectively.

Using R to Calculate a Probability Density

Just like the dbinom() function calculates the probability of a given observation from a binomial distribution by handling the math for us, the dnorm() function calculates the probability density of an observation from a normal distribution by plugging the values into Equation (1).

For example, dnorm(x = .4, mean = .5, sd = .1) computes the probability density by plugging in \(0.4\) for \(x\), \(0.5\) for \(\mu\), and \(0.1\) for \(\sigma\), returning 2.42.

The Probability Density of a Sample Mean

Remember that the standard deviation of the sampling distribution is called the standard error. The standard error for a sample of size n from a normal distribution is given by \(\frac{\sigma}{\sqrt{n}}\).

To calculate the probability density of a sample mean, we substitute \(\sigma\) in Equation (1) with the standard error \(\frac{\sigma}{\sqrt{n}}\). For instance, the probability density that a random draw from a normal distribution with \(\mu = 0.5\) and \(\sigma = 0.1\) equals 0.4 is:

dnorm(x = .4, mean = .5, sd = .1)
= 2.42.

By contrast, the probability density that the mean of a sample of size 25 from the distribution equals 0.4 is:

• dnorm(x = .4, mean = .5, sd = .1 / sqrt(25)) =
  
• dnorm(x = .4, mean = .5, sd = .02) =
  
• \(7.43 \times 10^{-5}\)

You should definitely know that the standard deviation of a normal sampling distribution, \(\sigma_\overline{x}\) (also known as the standard error), is the standard deviation divided by the square root of the sample size: \(\sigma_\overline{x} = \frac{\sigma}{\sqrt{n}}\)

The Standard Normal Distribution and the Z-Transform

The most well-known normal distribution, the “standard normal distribution” (also known as Z), has a mean of zero and a standard deviation of one. That is, \(X \sim N(0,1)\).

Any normal distribution can be converted to the standard normal distribution by subtracting the population mean, \(\mu\), from each value and dividing by the population standard deviation, \(\sigma\) — this process is known as the Z-transform.

\[Z = \frac{X - \mu}{\sigma}\]

For example, using the Z-transform, a value of \(X = 0.4\) from a normal distribution with \(\mu = 0.5\) and \(\sigma = 0.1\) would be:

\[\frac{0.4 - 0.5}{0.1} = \frac{-0.1}{0.1} = -1.\]

The Z-transform is useful because it provides a simple way to interpret results on a common scale. I think of a Z-value as the number of standard deviations between an observation and the population mean.

Properties of a normal distribution

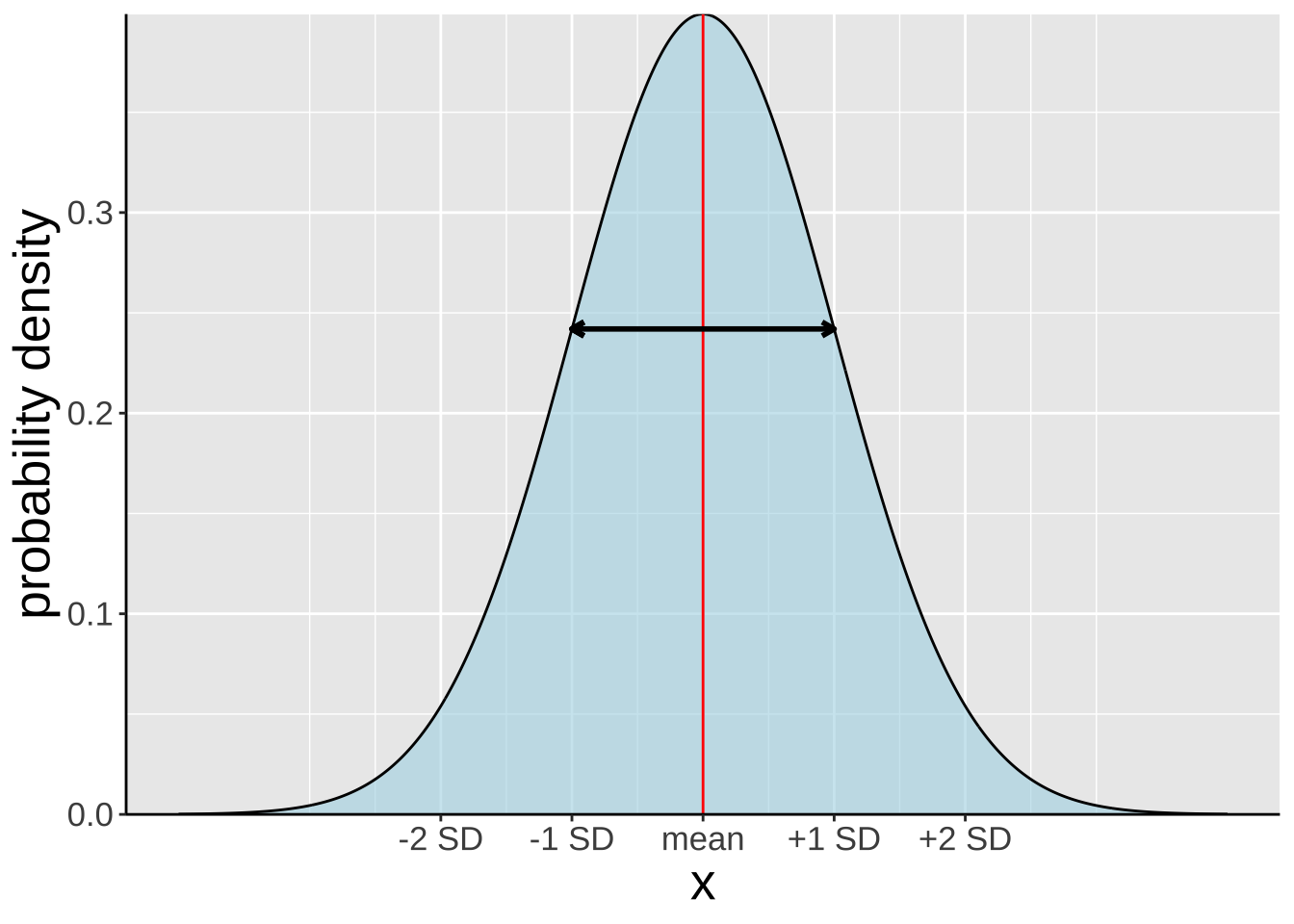
Figure 3: Any old normal distribution.

A Normal Distribution is Symmetric About its Mean

This means:

1. Half of the normal distribution lies above the mean, and half lies below it. For example, if \(X \sim N(0.5, 0.1^2)\):
   • pnorm(q = 0.5, mean = 0.5, sd = 0.1, lower.tail = TRUE) =
     
   • pnorm(q = 0.5, mean = 0.5, sd = 0.1, lower.tail = FALSE) =
     
   • 0.5.
2. The probability density of being a certain distance away from the mean is the same in either direction. For example:
   • dnorm(x = 0.4, mean = 0.5, sd = 0.1) =
     
   • dnorm(x = 0.6, mean = 0.5, sd = 0.1) =
     
   • 2.4197.
3. The probability of being a certain distance away from the mean (or more extreme) is the same whether you’re below or above the mean. For example:
   • pnorm(q = 0.4, mean = 0.5, sd = 0.1, lower.tail = TRUE) =
     
   • pnorm(q = 0.6, mean = 0.5, sd = 0.1, lower.tail = FALSE) =
     
   • 0.1587.

Probability that X Falls Within a Range

The probability that X lies between two values, \(a\) and \(b\), is given by:

\[P[a < X < b] = \int_{a}^{b} \frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{-\frac{(x-\mu) ^{2}}{2\sigma ^{2}}} dx\]

Some helpful (approximate) ranges:

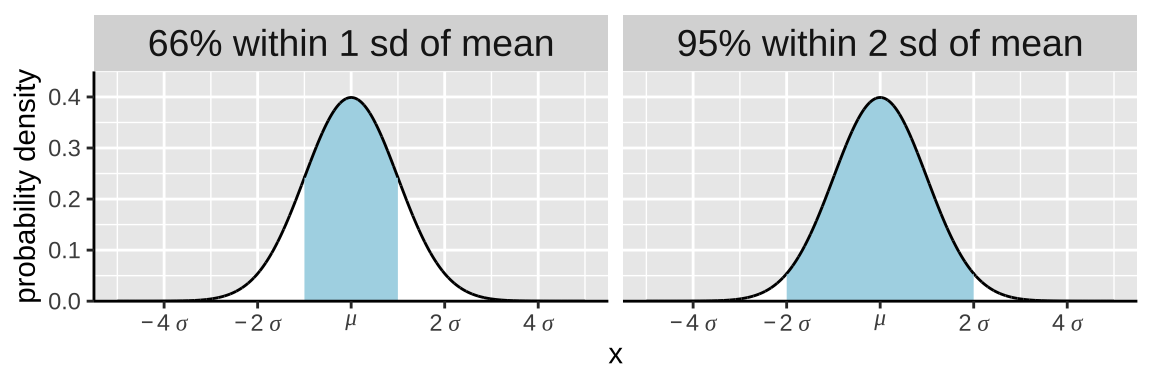
More exactly, the probability that X is within one standard deviation away from the mean equals

• The probability it is not more than one standard deviation less than its mean
  • pnorm(q = -1, mean = 0, sd = 1, lower.tail = FALSE)
    
  • = 0.8413
    
• Minus the probability it is not more than one standard deviation greater than its mean
  • pnorm(q = 1, mean = 0, sd = 1, lower.tail = FALSE)
    
  • = 0.1587.
    
• Which equals
  • 0.841 - 0.158
    
  • = 0.683

For this example we used the standard normal distribution for ease, but this is true for any normal distribution… e.g. pnorm(q = 10, mean = 5, sd = 5, lower.tail = FALSE) = 0.1587.

Probability that a mean, \(\overline{X}\), falls in a range

Again, we can take advantage of the fact that the standard deviation of a sampling distribution is the standard error divided by the square root of the sample size. So the probability that a mean, \(\overline{X}\) lies between two values, \(a\) and \(b\) is \[P[a < \overline{X} < b] = \int_{a}^{b} \frac{1}{\sqrt{2\pi \sigma ^{2}/n}}e^{-\frac{(x-\mu) ^{2}}{2\sigma ^{2}/n}} dx\].

So, for example, the probability that the mean of four draws from the standard normal distribution is between -1 and 1 is

• The probablity is is greater than negative one
  • pnorm(q = -1, mean = 0, sd = 1/sqrt(4), lower.tail = FALSE)
    
  • rpnorm(q = -1, mean = 0, sd = 1/sqrt(4), lower.tail = FALSE) %>% round(digits = 4)`
    
• Minus the probablity is greater than one
  • pnorm(q = 1, mean = 0, sd = 1/sqrt(4), lower.tail =FALSE)
    
  • 0.0228
• Equals \(0.977 - 0.022 = 0.955\)

Let’s prove this to ourselves by generating four random numbers from the standard normal distribution many times using rnorm()

# set up
n_reps      <- 100000
sample_size <- 4
this_mean   <- 0
this_sd     <- 1

tibble(sample = rep(1:n_reps, each = sample_size),
       value  = rnorm(n = n_reps * sample_size, mean = this_mean, sd = this_sd)) %>%
  group_by(sample)                              %>%
  summarise(mean_x          = mean(value))      %>%
  mutate(within_one         = abs(mean_x) < 1 ) %>%
  summarise(prop_within_one = mean(within_one))

# A tibble: 1 × 1
  prop_within_one
            <dbl>
1           0.956

Quantiles of a Normal Distribution

Above, I mentioned that about 95% of samples are within two standard deviations of the mean in a normal distribution. This is a close approximation. As demonstrated earlier, we can calculate the proportion of samples within two standard deviations of the mean using pnorm(q = 2, mean = 0, sd = 1) - pnorm(q = -2, mean = 0, sd = 1) which equals 0.9544997.

Now, let’s reverse the question and find the values that separate the middle 95% of samples from the extremes (i.e., the critical values for \(\alpha = 0.05\)). The qnorm() function (where “q” stands for quantile) helps us here. We can find a two-tailed critical value with qnorm(p = 1 - alpha/2, mean = 0, sd = 1), where \(\alpha\) is the specified significance level, and we divide by two because we’re considering equal areas in both tails. Therefore, 95% of samples (of size one) from a normal distribution lie within qnorm(p = 1 - 0.05/2, mean = 0, sd = 1) = 1.96 standard deviations from the mean.

Is it normal?

Much of the statistics we will soon learn relies, to some extent, on normal data (or more specifically, a normally distributed sampling distribution of residuals). While there are statistical procedures to test the null hypothesis that data come from a normal distribution, we rarely use these because deviations from normality can be most critical when we have the least power to detect them. For this reason, we typically rely on visual inspection rather than null hypothesis significance testing to assess whether data are approximately normal.

“Quantile-Quantile” plots and the eye test

In a “quantile-quantile” (QQ) plot, the x-axis represents the z-transformed expectation of y, i.e., mutate(data, qval = rank(y)/(n + 0.5), x = qnorm(qval)), and the y-axis represents the data. Data from a normal distribution should fall near a straight line.

In R, we can create a QQ-plot using the geom_qq() function and add a line with geom_qq_line(). Here, we map our quantity of interest onto the sample attribute. As an example, Figure 4 shows a QQ-plot of petal lengths in Iris versicolor.

iris %>%
  filter(Species == "versicolor") %>%
  ggplot(aes(sample = Petal.Length)) +
  geom_qq() +
  geom_qq_line()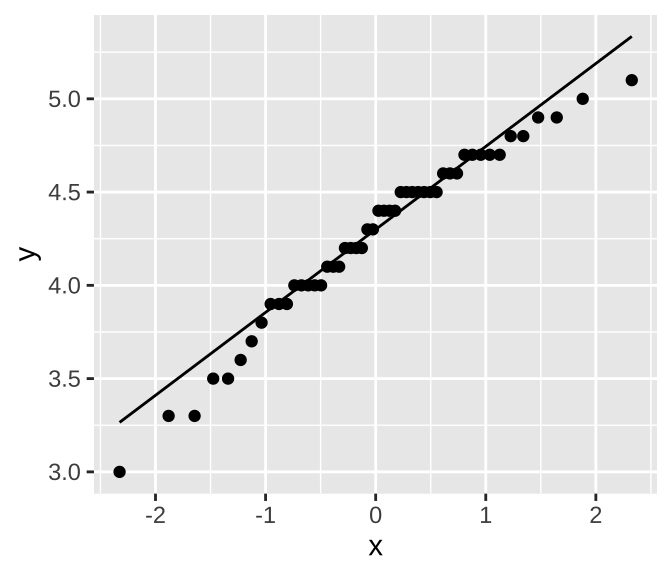

Figure 4: A quantile-quantile plot of Petal Length in Iris versicolor.

We can see that the points are fairly close to the predicted line, although both the small and large values are slightly smaller than expected. Is this a big deal? Is this deviation surprising? To answer that, we need to understand the variability we expect from a normal distribution.

What normal distributions look like

I’m always surprised by how easily I can convince myself that a sample doesn’t come from a normal distribution. Try hitting the Generate a sample from the normal distribution button in the app below a few times, and experiment with the sample size to get a sense of the variability in what samples from a normal distribution can look like.

Figure 5: Run this about ten times with five different sample sizes to get a sense of the variability in how normal a sample from the normal distribution can appear. This process takes your sample size, n, and simulates random data from the standard normal distribution using the following R code: my_dat <- tibble(x = rnorm(n = n, mean = 0, sd = 1)), and then plots the output.

Examples of a sample not from a normal distribution

Let’s compare the samples from a normal distribution, in Figure 5 to cases in which the data are not normal. For example,

• Figures 6A-D makes it clear that across the three Iris species, sepal length is bimodal.
• Figure 6E-H makes it clear that across all mammals the distribution of body weights are exponentially distributed.

These examples are a bit extreme. Over the term, we’ll get practice in visually assessing if data are normallish.

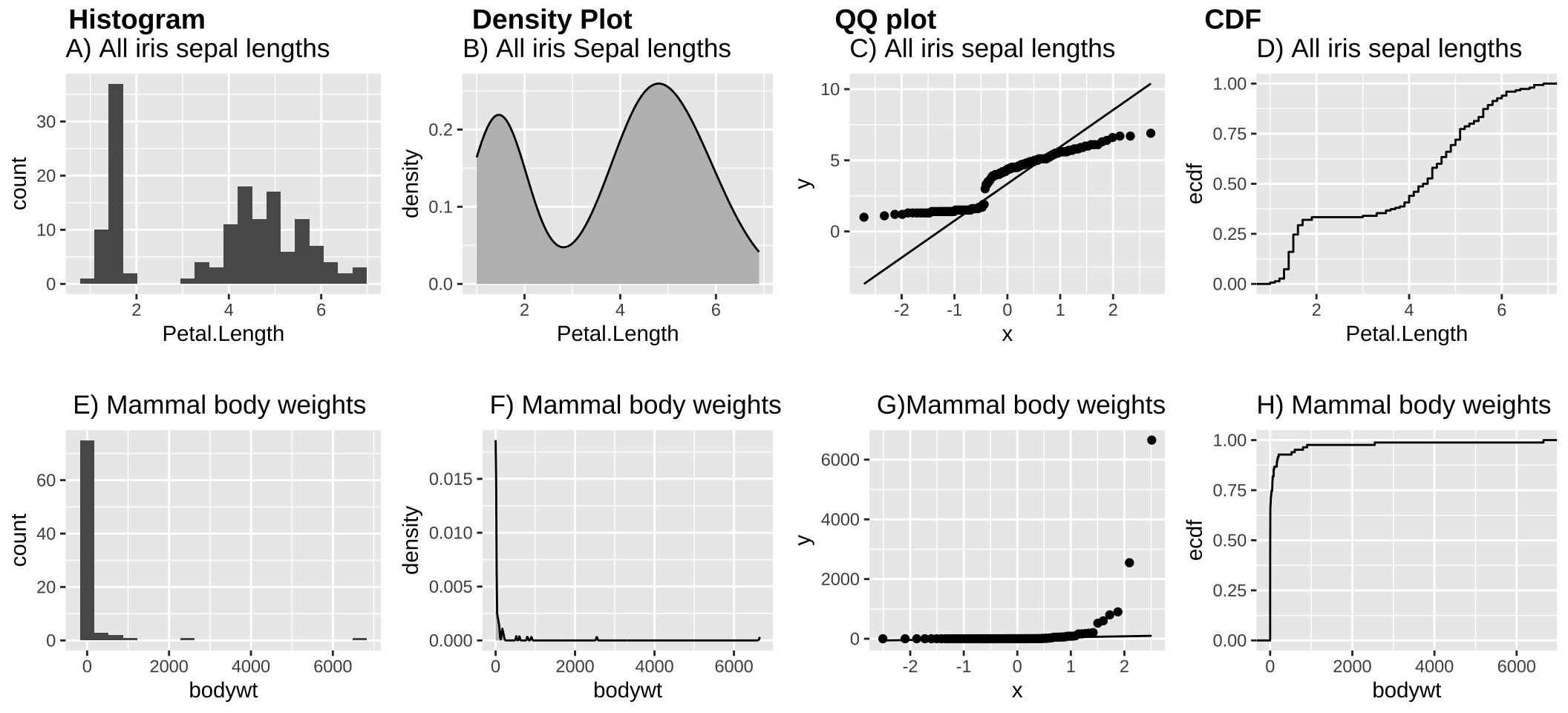
Figure 6: (A-D) The distribution of petal lengths across all three iris species is bimodal – as the extremely small petals of iris setosa sticks out. (E-H) The distribution of mammal body size is exponentially distributed.

Why Normal Distributions Are Common

One amazing thing about the world is just how frequently normal distributions occur. The reason for this is that whenever a value results from adding up MANY INDEPENDENT factors, that value will follow a normal distribution, regardless of the underlying distribution of these individual factors. For example, your height is influenced by many genes in your genome, as well as numerous environmental factors, all contributing to this outcome.

An important consequence of this is that the sampling distribution of means tends to be normally distributed, provided the sample size isn’t too small. This principle, known as the Central Limit Theorem, is very useful in statistics. It allows us to create reasonable statistical models of sample means by assuming normality, even when the underlying data may not be perfectly normal.

The Central Limit Theorem is crucial for statistics because many of the statistical analyses we perform, which assume normality, are still valid even if the underlying data are not perfectly normal. This enables us to model complex scenarios by assuming normality.

How Large Must a Sample Be for Us to Trust the Central Limit Theorem?

The Central Limit Theorem assures us that with a sufficiently large sample size, the sampling distribution of means will be normal, regardless of the distribution of the underlying data points.

But how large is sufficiently large? The answer depends on how far from normal the initial data are. The less normal the original data, the larger the sample size needed before the sampling distribution becomes normal.

Figure 7: The sampling distribution of a sample of size, sample size, from a few different distributions. A sample of size one corresponds to the raw data, while all other sample sizes show a sampling distribution. For each distribution, explore how many samples we need before the sampling distribution looks normal.

Transforming Data

Because the normal distribution is so common, and because the Central Limit Theorem is so useful, many statistical approaches are built on the assumption of some form of normality. However, sometimes data are too far from normal to be modeled as if they are normal. Other times, certain characteristics of the data’s distribution may break other assumptions of statistical tests. When this happens, we have a few options:

1. We can permute and bootstrap!
   
2. We can use or develop tools to model the data based on their actual distribution.
   
3. We can transform the data to better meet our assumptions.
   
4. We can use robust and/or nonparametric approaches.

We have already discussed option 1 at length, and will return to options 3 and 4 later in the term.

Rules for Legitimate Transformations

There is nothing inherently “natural” about the linear scale, so transforming data to a different scale is perfectly valid. In fact, we should estimate and test hypotheses on a meaningful scale. Often, an appropriate transformation will result in data that are more “normal-ish.” Effective transformations are guided by the characteristics of the data, the processes that generated them, and the specific questions being addressed, ensuring that the transformation makes sense in context.

Rules for Transforming Data:

• Let biology guide you. Often, you can determine an appropriate transformation by considering a mathematical model that describes your data. For example, if values naturally grow exponentially, a log transformation may be appropriate.
  
• Apply the same transformation consistently to each individual in the dataset.
  
• Transformed values must have a one-to-one correspondence with the original values. For example, don’t square values if some are less than 0 and others greater than 0.
  
• Transformed values must maintain a monotonic relationship with the original values. This means that the order of the values should be preserved after the transformation—larger values in the original data should remain larger after the transformation.
  
• Conduct your statistical tests after you settle on the appropriate transformation.
  
• Be cautious not to bias your results by inadvertently losing data points. This can happen, for example, if a log transformation fails on zero or negative values, or when extreme values are removed during the transformation process.

Common Transformations

There are several common transformations that can make data more normal, depending on their initial shape:

Name	Formula	What type of data?
Log	\(Y'=\log_x(Y + \epsilon)\)	Right skewed
Square-root	\(Y'=\sqrt{Y+1/2}\)	Right skewed
Reciprocal	\(Y'=1/Y\)	Right skewed
Arcsine	\(\displaystyle p'=arcsin[\sqrt{p}]\)	Proportions
Square	\(Y'=Y^2\)	Left skewed
Exponential	\(\displaystyle Y'=e^Y\)	Left skewed

Notes:
- Log transformations handle right-skewed data well, but be sure to add a small constant (\(\epsilon\)) to avoid taking the log of zero or negative numbers. - Arcsine transformations are specifically useful for proportions between 0 and 1, but can be problematic near the boundaries (values close to 0 or 1) due to the transformation’s behavior at these points.

Transformation example: The log transformation

We have seen that the normal distribution arises when we add up a bunch of things. If we multiply a bunch of things, we get an exponential distribution. Because adding logs is like multiplying untransformed data, a log transform makes exponential data look normal.

Take our distribution of mammal body weights, for example. It is initially far from normal (Fig. 8A,C), but after a log transformation it is much closer to normal (Fig. 8B,D) and would likely have a normal sampling distribution for relatively modest sample sizes.

# log10 transform
msleep <-  mutate(msleep, log10_bodywt = log10(bodywt))

# let's evaluate normality          
plot_grid(
  ggplot(msleep, aes(x = bodywt))            + geom_histogram() + labs(title = "Raw body weight"),
  ggplot(msleep, aes(x = log10_bodywt))      + geom_histogram() + labs(title = "log10(body weight)") ,
  ggplot(msleep, aes(sample = bodywt))       + geom_qq()        + geom_qq_line() ,
  ggplot(msleep, aes(sample = log10_bodywt)) + geom_qq()        + geom_qq_line() ,
  ncol =2, labels = "AUTO", rel_heights = c(5,4.5))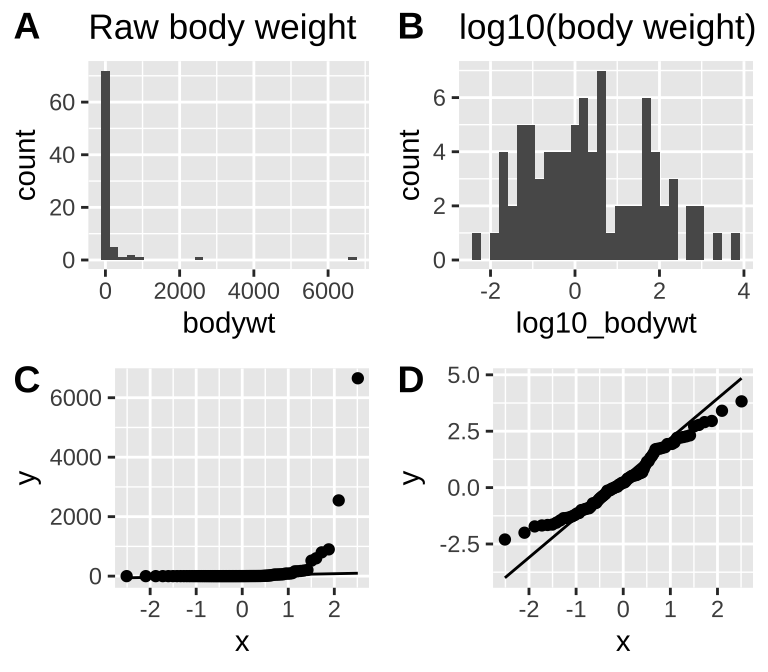

Figure 8: The mammal body mass data is very far from normal as seen in the histogram (A) and qq-plot (C). After log_10 transformation, data are much closer to normal (B and D). log_10 was chosen over the natural log because it is easier for most readers to interpret

Be careful when log-transforming!! All data with a value of zero or less will disappear. For this reason, we often use a log1p transform, which adds one to each number before logging them.

Quiz

Figure 9: Quiz here

[Optional] Log Likelihood of \(\mu\)

Later on, we’ll see that calculating likelihoods is the foundation of both maximum likelihood and Bayesian inference. But how can we calculate likelihoods for a parameter of a normal distribution? Let’s take a look!

Imagine we have a sample with values 0.01, 0.07, and 2.2, and we know the population standard deviation is one, but we don’t know the population mean. To calculate the likelihood of a proposed mean, we multiply the probability of each observation given that proposed mean. For example, the likelihood of \(\mu = 0\) when \(\sigma = 1\) and the data are \(\{0.01, 0.07, 2.2\}\) is:

dnorm(x = 0.01, mean = 0, sd = 1) * dnorm(x = 0.07, mean = 0, sd = 1) * dnorm(x = 2.20, mean = 0, sd = 1)

[1] 0.00563186

A more concise way to express this is:

dnorm(x = c(0.01, 0.07, 2.20), mean = 0, sd = 1) %>% prod()

[1] 0.00563186

Remember, we multiply the probabilities because all the observations are independent.

For both mathematical reasons (e.g., working with small numbers) and computational efficiency, it’s often better to work with log likelihoods instead of likelihoods on the linear scale. Multiplication on the linear scale translates to addition on the log scale. So, the log likelihood for this case is:

dnorm(x = c(0.01, 0.07, 2.20), mean = 0, sd = 1, log = TRUE) %>% sum()

[1] -5.179316

This evaluates to -5.1793156. To check, note that log(0.00563186) equals -5.1793155.

We can generate a likelihood profile by plotting how the log likelihood changes as we vary the proposed mean:

obs            <- c(0.01, 0.07, 2.2)
proposed.means <- seq(-1, 2, .001)
tibble(proposed_means = rep(proposed.means , each = length(obs)),
       observations   = rep(obs, times = length(proposed.means)),
       log_liks       = dnorm(x = observations, mean = proposed_means, sd = 1, log = TRUE)) %>%
  group_by(proposed_means) %>%
  summarise(logLik = sum(log_liks)) %>%
  ggplot(aes(x = proposed_means, y = logLik))+
  geom_line()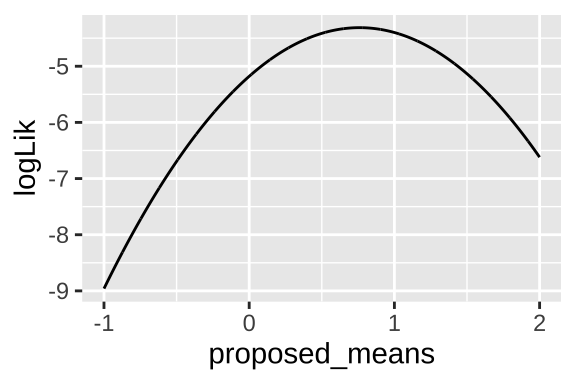

To find the maximum likelihood estimate (MLE) of the mean:

tibble(proposed_means = rep(proposed.means , each = length(obs)),
       observations   = rep(obs, times = length(proposed.means)),
       log_liks       = dnorm(x = observations, mean = proposed_means, sd = 1, log = TRUE)) %>%
  group_by(proposed_means) %>%
  summarise(logLik = sum(log_liks)) %>%
  filter(logLik == max(logLik)) %>%
  pull(proposed_means)

[1] 0.76

This will give us the MLE, which equals the sample mean: mean(c(0.01, 0.07, 2.2)) = 0.76. More generally, for normally distributed data, the maximum likelihood estimate of the population mean is the sample mean.