Motivating Scenario:
We have numerous continuous explanatory variables and aim to develop a comprehensive model.
Learning Goals: By the end of this chapter, you should be able to:
- Write and interpret linear models with two predictors.
- Conduct and interpret a polynomial regression in R.
- Conduct and interpret two-factor ANOVAs in R.
- Calculate Type I sums of squares.
- Calculate Type II sums of squares.
Review of Linear Models
A linear model predicts the response variable, \(\widehat{Y_i}\), by summing all components of the model:
\[ \hat{Y_i} = a + b_1 y_{1,i} + b_2 y_{2,i} + \dots{} \]
Linear Models We Have Covered
- One-sample t-tests: \(\widehat{Y} = \mu\)
- Two-sample t-tests: \(\widehat{Y_i} = \mu + A_i\) (\(A_i\) can take one of two values)
- ANOVA: \(\widehat{Y_i} = \mu + A_i\) (\(A_i\) can take one of more than two values)
- Regression: \(\widehat{Y_i} = \mu + X_i\) (\(X_i\) is continuous)
So far, we’ve primarily modeled a continuous response variable as a function of a single explanatory variable. However, linear models can include multiple predictors. For example, we could predict Dragon Weight as a function of both a categorical variable (e.g., spotted: yes/no) and a continuous variable in the same model.
Test Statistics for a Linear Model
- The \(t\) value shows how many standard errors an estimate is from its null value.
- The \(F\) value quantifies the ratio of variation in the response variable associated with a focal explanatory variable (\(MS_{model}\)), relative to the variation not attributable to this variable (\(MS_{error}\)).
Assumptions of a Linear Model
Linear models rely on the following assumptions:
- Linearity: The observations are appropriately modeled by summing all predictions in our equation.
- Homoscedasticity: The variance of residuals is constant across values of the predicted value, \(\hat{Y_i}\).
- Independence: Observations are independent of one another (aside from the model’s predictors).
- Normality: Residuals are normally distributed.
- Unbiased Data Collection: Data should be collected without bias.
Polynomial Regression Example
Linear models can incorporate terms like squared or other nonlinear transformations, as long as predictions result from adding all model components. A common example is polynomial regression, where the response variable is predicted as a function of the predictor and higher-order terms, often including the explanatory variable and its square, as shown below.
\[\begin{equation} \begin{split} \widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times X_{2,i}\\ \\ \text{ where } X_{2,i} = X_{1,i}^2 \end{split} \tag{1} \end{equation}\]
Polynomial Regression Example
Let’s revisit our example of polynomial regression, where we predict the number of species from the productivity of a plot to work through these ideas. Recall that:
- A simple linear regression did not fit the data well and violated regression assumptions, as residuals were large and positive for intermediate predictions and large and negative for small or large predictions.
- Including a squared term improved the model fit and allowed the data to meet assumptions.
Let’s write a descriptive equation for each model:
\[\text{N.SPECIES = CONSTANT + PRODUCTIVITY}\] \[\text{N.SPECIES = CONSTANT + PRODUCTIVITY + PRODUCTIVITY}^2\]
We present these models in Figure 1. Note that we can add a polynomial fit to our ggplot by including formula = y ~ poly(x, 2, raw = TRUE) in the geom_smooth function.
bmass <- tibble( Biomass = c(192.982,308.772,359.064,377.778,163.743,168.421,128.655,98.246,107.602,
93.567,83.041,33.918,63.158,139.181,148.538,133.333,127.485,88.889,138.012),
n.species = c(25.895,12.729,8.342,2.885,21.504,20.434,18.293,16.046,16.046,11.655,
12.725,9.515,7.16,16.042,16.042,11.655,12.725,2.88,8.338))
base_plot <- ggplot(bmass, aes(x = Biomass, y = n.species))+ geom_point()+ xlab("Productivity (g/15 Days)" )
linear_plot <- base_plot + labs(title = "Linear term") +
geom_smooth(method = 'lm')
polynomial_plot <- base_plot + labs(title = "Linear and squared term") +
geom_smooth(method = 'lm',formula = y ~ poly(x, 2, raw = TRUE))
plot_grid(linear_plot, polynomial_plot, labels = c("a","b"))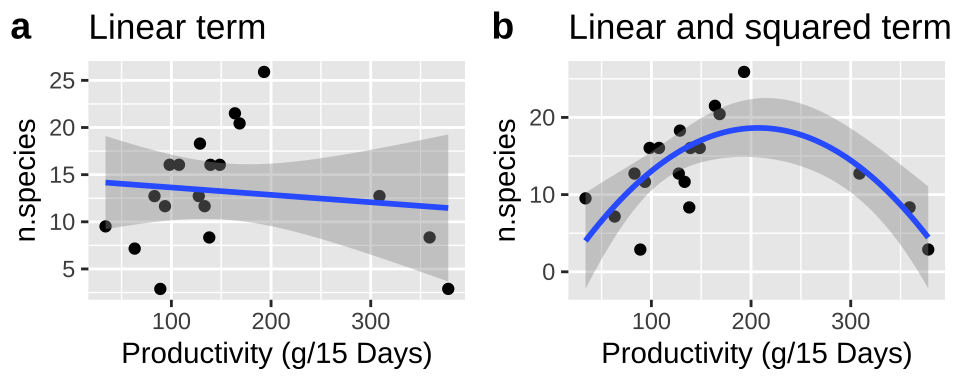
Figure 1: (A) Fitting a linear regression to predict the number of plant species from productivity of a plot. (B) Adding a squared term to our linear regression.
Fitting Polynomial Regressions in R
Fitting a model with a linear term in R should look familiar:
Call:
lm(formula = n.species ~ Biomass, data = bmass)
Residuals:
Min 1Q Median 3Q Max
-10.8481 -3.9559 -0.7005 2.7449 12.9831
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.425079 2.777151 5.194 7.31e-05 ***
Biomass -0.007841 0.015369 -0.510 0.616
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.167 on 17 degrees of freedom
Multiple R-squared: 0.01508, Adjusted R-squared: -0.04286
F-statistic: 0.2603 on 1 and 17 DF, p-value: 0.6165There are several ways to add a polynomial term:
lm(n.species ~ poly(Biomass, degree = 2, raw = TRUE), bmass): This is what we typed into ourgeom_smoothfunction above. Settingdegree = 3would add a cubed term as well.lm(n.species ~ Biomass + I(Biomass^2), bmass): This is a more explicit way to do this. When performing math on variables in a linear model, wrap them inI()to avoid R interpreting the syntax incorrectly.lm(n.species ~ Biomass + Biomass2, bmass %>% mutate(Biomass2 = Biomass^2)): Alternatively, usemutateto add a squared transformation before fitting the model. NOTE: I did not pipemutateintolm()becauselm()does not accept the standard%>%pipe. To use%>%, load themagrittrpackage and use%$%as inbmass %>% mutate(Biomass2 = Biomass^2) %$% lm(n.species ~ Biomass + Biomass2).
Interpreting the Output of a Polynomial Regression — Model Coefficients
Now, let’s examine this polynomial regression:
poly_term <- lm(n.species ~ Biomass + I(Biomass^2), bmass)
summary.lm(poly_term)
Call:
lm(formula = n.species ~ Biomass + I(Biomass^2), data = bmass)
Residuals:
Min 1Q Median 3Q Max
-8.9394 -1.4605 -0.3453 2.5914 7.3527
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.2887063 4.4420728 -0.515 0.613435
Biomass 0.2020729 0.0511573 3.950 0.001146 **
I(Biomass^2) -0.0004878 0.0001161 -4.200 0.000678 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.384 on 16 degrees of freedom
Multiple R-squared: 0.5316, Adjusted R-squared: 0.473
F-statistic: 9.078 on 2 and 16 DF, p-value: 0.002318The output should look familiar, with rows for:
(Intercept): The predicted number of species at zero productivity. This value of -2.29 emphasizes not making predictions outside the data range—species counts cannot be negative.Biomass: This describes how the number of species changes linearly with productivity. It’s critical to note that this does not imply species counts always increase with productivity because of the next term.Biomass2: This term shows how species counts change with the square of productivity. The negative sign indicates that species counts decrease with productivity squared. Polynomial regressions are often useful in such cases, where intermediate values are the largest or smallest, resulting in contrasting signs for linear and squared terms.
Writing down this equation, we predict species count as:
\[\widehat{n.species}_i = -2.29 + 0.202 \times Biomass_i -0.000488 \times Biomass_i^2\]
For example, with a plot productivity of 250 g/15 days, we would predict:
\[ \begin{split} \widehat{n.species}_{|Biomass=250} &= -2.29 + 0.202 \times 250 - 0.000488 \times 250^2\\ &= 17.71 \end{split} \]
A reasonable value, as it aligns with our curve intersecting 250 in Figure ??B.
Our columns (Estimate, Std. Error, t value, Pr(>|t|)) should feel familiar. The standard error indicates uncertainty in the estimate, the t-value shows how far the estimate is from zero in standard errors, and the p-value gives the probability of seeing such a deviation from zero under the null hypothesis. However:
The p-values in this output do not describe the statistical significance of the predictors! Do not interpret these p-values as such.
For instance, in our simple linear model, biomass and species count show no strong association, with the association being slightly negative.
broom::tidy(linear_term) %>%
mutate(across(estimate:statistic, round, 4), p.value = round(p.value, 5)) %>%
kable()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 14.4251 | 2.7772 | 5.1942 | 0.00007 |
| Biomass | -0.0078 | 0.0154 | -0.5102 | 0.61648 |
Note: The summary.lm() output still usefully provides our estimates and their uncertainties—so it’s worth consulting!
An ANOVA approach
So how do we get significance of each term? We look at the ANOVA output!
anova(poly_term)Analysis of Variance Table
Response: n.species
Df Sum Sq Mean Sq F value Pr(>F)
Biomass 1 9.90 9.90 0.5151 0.4832884
I(Biomass^2) 1 339.02 339.02 17.6417 0.0006782 ***
Residuals 16 307.47 19.22
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We now conclude that the association between n.species and the linear term of Biomass would be quite expected from the null. How do we square these ideas? I think of the significance of the linear term as how weird it would be to see a non-zero linear estimate in the absence of a squared term. However, this is not fully correct, as this P-value differs from the one above with just the linear term. To make sense of this, let’s dig into how we calculate the sums of squares for these larger models.
“Sequential” Type I Sums of squares
We’ll see in this and the next section that there’s a real issue in which variable we attribute our sums of squares to in larger linear models.
In many cases (see below) Sequential “Type I” sums of squares make the most sense. Here we
- Calculate \(SS_{error}\) and \(SS_{total}\) as we always do! (Figure 2A,D)
- Calculate the \(SS_{thing1}\) (in this case Biomass), as if it where the only thing in the model, \(\widehat{Y_{i|bmass}}\). (Figure 2B).
- Calculate the \(SS_{thing2}\) (in this case \(Biomass^2\)), as the deviation of predicted values from a model with both things in it, \(\widehat{Y_{i|bmass,bmass^2}}\), minus predictions from a model with just thing1 in it, \(\widehat{Y_{i|bmass}}\) (Figure 2C).
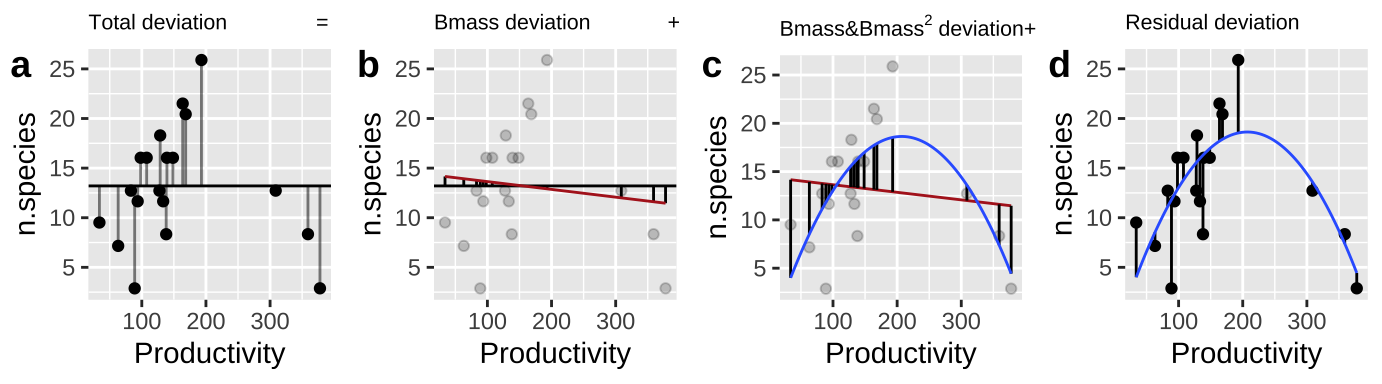
Figure 2: Calculating sequential sums of squares for our model. a Total deviations, as usual. b Deviations from predicted values of Biomass alone without considering the squared term (red line) – this makes up \(SS_{Biomass}\). c Deviations of predictions from \(Biomass + Biomass^2\) (blue line) away from predictions of Biomass alone (red line) – this makes up \(SS_{Biomass^2}\). d Deviation of data points from full model (blue line) – this makes up \(SS_{error}\)
We can calculate these sums of squares in R as follows, and then compute mean squares and p-values. Before I do this, I make a tibble with prediction from both the simple linear model with just a linear term, and the fuller linear model with the linear and squared term.
combine_models <- full_join(augment(linear_term) %>%
dplyr::select(n.species, Biomass, .fitted_lin = .fitted, .resid_lin = .resid),
augment(poly_term) %>%
dplyr::select(n.species, Biomass, .fitted_full = .fitted, .resid_full= .resid),
by = c("n.species", "Biomass"))
combine_models %>%
summarise(ss_tot = sum( (n.species - mean(n.species))^2 ),
ss_bmass = sum( (.fitted_lin - mean(n.species))^2 ),
ss_bmass2 = sum( (.fitted_full - .fitted_lin )^2 ),
ss_error = sum( (n.species - .fitted_full)^2 ),
#df
df_bmass = 1, df_bmass2 = 1, df_error = n() - 3,
#
ms_bmass = ss_bmass / df_bmass ,
ms_bmass2 = ss_bmass2 / df_bmass2 ,
ms_error = ss_error / df_error,
#
F_bmass = ms_bmass / ms_error, F_bmass2 = ms_bmass2/ ms_error,
p_bmass = pf(q = F_bmass, df1 = df_bmass, df2 = df_error, lower.tail = FALSE),
p_bmass2 = pf(q = F_bmass2, df1 = df_bmass2, df2 = df_error, lower.tail = FALSE)) %>% mutate_all(round,digits = 4) %>%DT::datatable( options = list( scrollX='400px'))You can scroll through the output above to see that our calculations match what anova() tells us!!!
Type I Sums of Squares (and others)
Calculating Sums of Squares sequentially, as we did in Figure 2, is the default way R does things.
Sequential Type I sums of squares calculate the sums of squares for the first thing in your model first, then the second thing, then the third thing etc… This means that while our
- Sums of square, Mean squares, F values, and p-values might change, depending on the order in which variables are entered into our model.
- Parameter estimates and uncertainty in them will not change with order.
In general sequential sums of squares make the most sense when
- We are not interested in the significance of the earlier terms in our model, which we want to take account of, but don’t really care about their statistical significance.
- Designs are “balanced” (Figure 3), as in these cases, we get the same SS, F and P values regardless of the order that we put terms into the model.
.](images/balanced-and-unbalanced-design.webp)
Figure 3: Examples of balanced and unbalanced statistical designs, from statistics how to.
Multiple regression.
In a way, a polynomial regression is a special type of multiple regression – we are predicting our continuous response variable as a function of two (?ish?) continuous predictors.
We also are often interested in predicting a continous response from two (or more) different explanatory variables
\[\begin{equation} \widehat{Y_i} = a + b_1 \times y_{1,i} + b_2 \times X_{2,i}\\ \\ \tag{2} \end{equation}\]
Multiple Regression Assumptions
Multiple regression models follow the same assumptions as any linear model:
- Homoscedasticity: The variance of residuals is constant across all levels of the predicted value, \(\hat{Y_i}\), meaning it remains consistent regardless of the values of the predictors.
- Independence: Observations are independent of each other, except as influenced by the predictors included in the model.
- Normality: Residuals are normally distributed.
- Unbiased Data Collection: Data are collected without systematic bias.
When we have more than one explanatory variable in our model (e.g., in a two-way ANOVA, ANCOVA, multiple regression, etc.), linear models additionally assume:
- Linearity: Observations are appropriately modeled by the sum of all predictions in the equation.
- Limited Multicollinearity: Predictor variables are not highly correlated; otherwise, interpreting estimates becomes challenging (more on this later).
Multiple Regression Example: Admixed Clarkia
Here, I present a snapshot of some ongoing research we are working on with collaborators Dave Moeller, Shelly Sianta, and Brooke Kern.
Over the past twenty years, research in speciation genomics has revealed that gene flow between sister taxa is quite common. We are investigating what factors influence the extent of gene flow between two sister species of Clarkia xantiana: Clarkia xantiana xantiana and Clarkia xantiana parviflora (hereafter referred to as xan and parv). These taxa show an interesting difference in reproductive biology:
- xan predominantly outcrosses, meaning it receives pollen from other individuals of the same (or even different) species.
- parv predominantly self-fertilizes, where one individual often pollinates itself.
Our study focuses on understanding what influences the amount of gene flow we observe. Specifically, we are interested in whether differences in traits within parv associated with its self-fertilization tendency (e.g., petal area, petal color, herkogamy—the distance between a flower’s male and female parts) impact the extent of gene flow. Additionally, we are curious to see if proximity to the other species (xan) increases gene flow.
To explore these questions, we sequenced the genomes of a number of plants, noting their collection locations and key phenotypic traits. Here, we will focus on parviflora plants from one population (Site 22) and examine:
Whether physical distance between a parviflora plant and the nearest xantiana plant influences the extent of admixture (i.e., the proportion of its genome derived from xantiana).
Whether herkogamy, the distance between male (anther) and female (stigma) parts, influences the extent of admixture. Our underlying biological idea is – if you’re fertilizing yourself you cannot be fertilized by the other species.
](images/parvxant.png)
Figure 4: Our species. Images taken from Calflora
The data
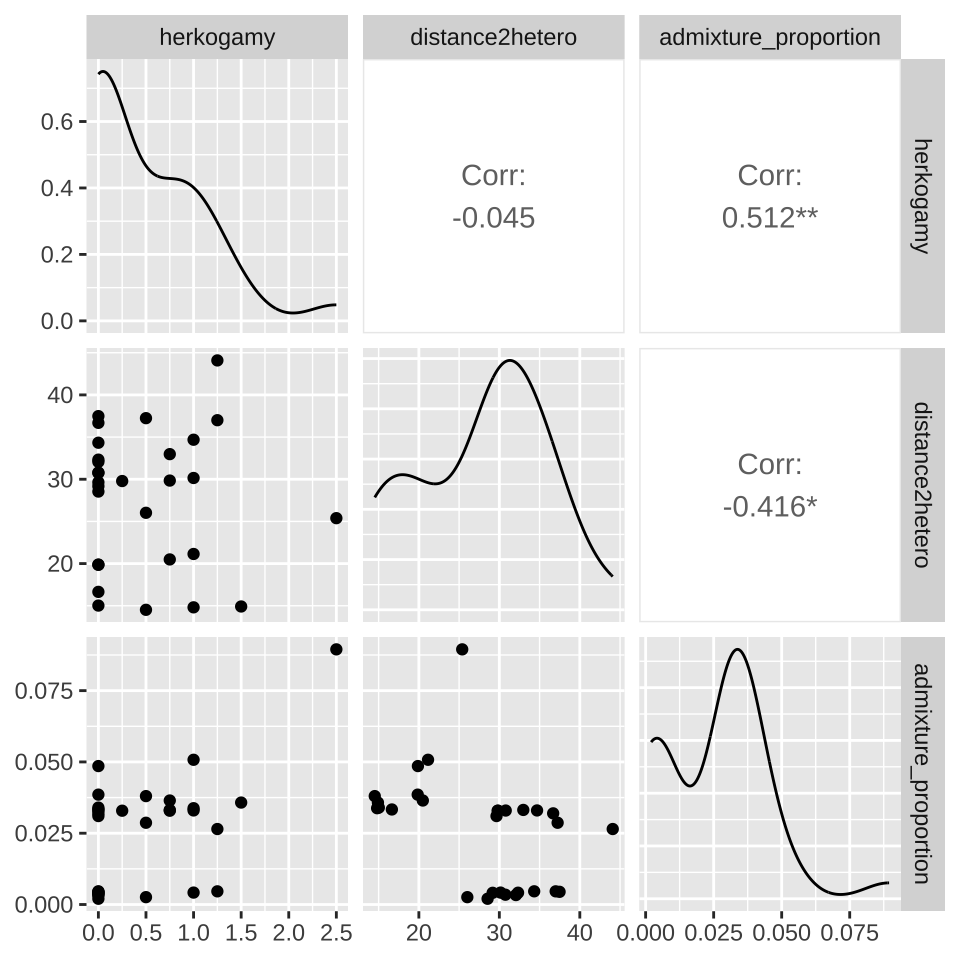
The data are available here. A quick plot shows that
- The admixture proportion appears to decrease as plants are further from the other species and
- The admixture proportion appears to increase as stigma are further from anthers
clarkia_link <- "https://raw.githubusercontent.com/ybrandvain/datasets/refs/heads/master/clarkia_admix_S22P.csv"
clarkia <- read_csv(clarkia_link)
a <- ggplot(clarkia,aes(x = herkogamy, y = admixture_proportion, color = distance2hetero))+
geom_point(size = 3, alpha = .72)+
geom_smooth(method = "lm") + scale_color_viridis_c(option = "viridis")+ theme_light()+ theme(axis.text = element_text(size = 12),axis.title = element_text(size = 15), legend.text = element_text(size = 12),legend.title = element_text(size = 15), legend.position = "bottom",legend.key.width = unit(1.5, "cm") )
b <- ggplot(clarkia,aes(x = distance2hetero, y =admixture_proportion, color = herkogamy))+
geom_point(size = 3, alpha = .72)+
geom_smooth(method = "lm") + scale_color_viridis_c(option = "plasma")+ theme_light()+ theme(axis.text = element_text(size = 12),axis.title = element_text(size = 15), legend.text = element_text(size = 12),legend.title = element_text(size = 15), legend.position = "bottom",legend.key.width = unit(1.5, "cm") )
a+b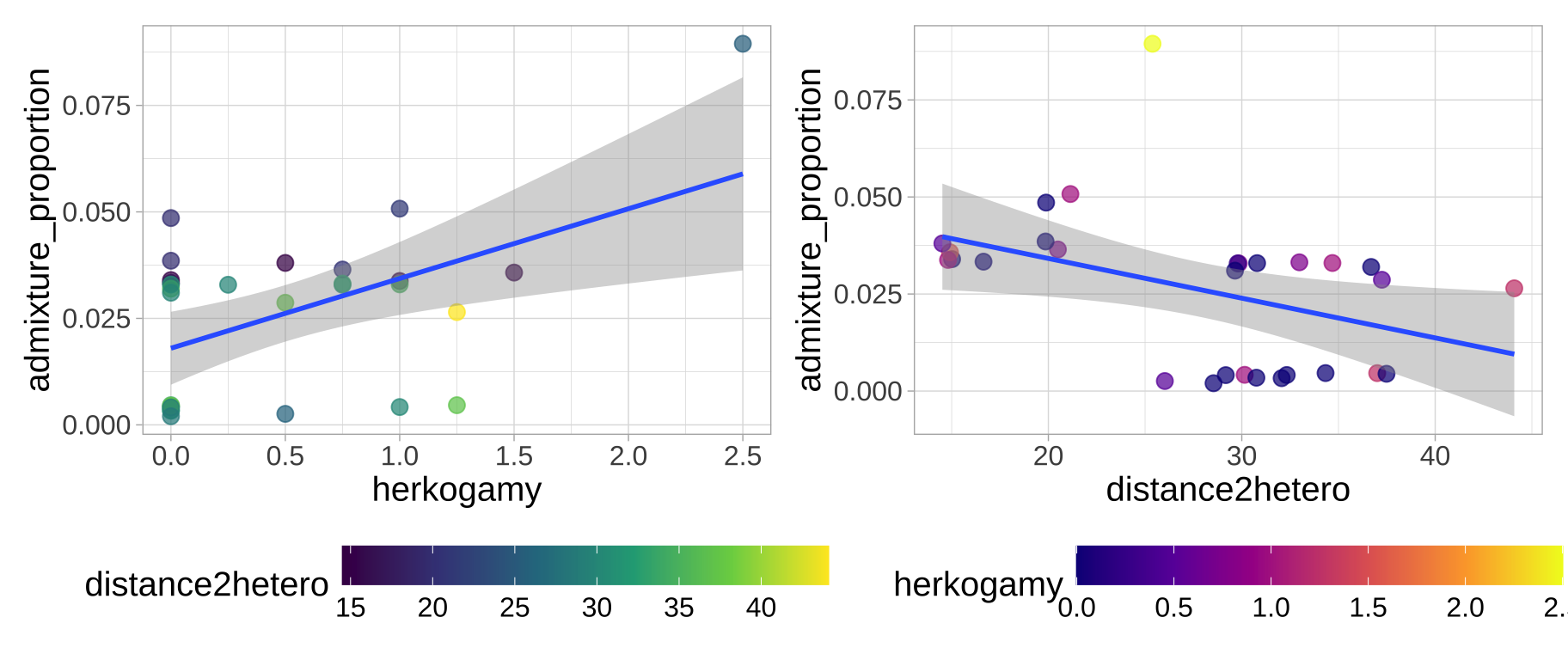
Or you can look at a bunch at once with the ggpairs() function in the GGally package.
Modeling Residuals
One way to approach multiple regression (especially when using Type II sums of squares, as discussed below) is by aiming to model the variation in each trait after accounting for the influence of the other. For example, if we’re interested in the effect of herkogamy on admixture while accounting for the effect of distance2hetero, we can model the residuals from a model of Admixture = f(distance2hetero) as a function of herkogamy (and vice versa).
model_distance2hetoro <- lm(admixture_proportion ~ distance2hetero, data = clarkia)
augment(model_distance2hetoro)%>%
mutate(herkogamy = pull(clarkia, herkogamy)) %>%
ggplot(aes(x = herkogamy, y = .resid))+
geom_point(size= 3, alpha = .7)+
geom_smooth(method = "lm") + theme(axis.text = element_text(size = 12),axis.title = element_text(size = 15))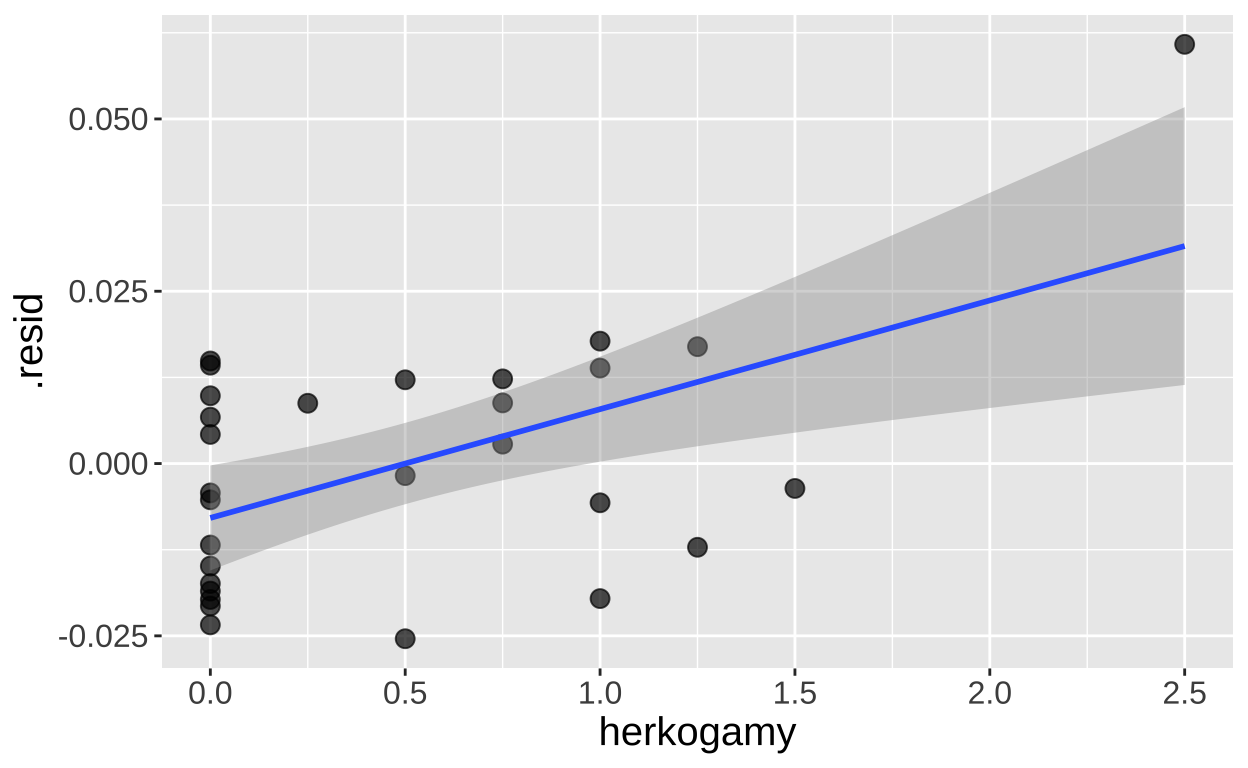
augment(model_distance2hetoro)%>%
mutate(herkogamy = pull(clarkia, herkogamy)) %>%
lm(.resid ~ herkogamy, data = .)%>%
tidy() %>% mutate_at(2:5, round, digits =4) %>% kbl()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -0.0079 | 0.0037 | -2.125 | 0.0429 |
| herkogamy | 0.0158 | 0.0047 | 3.360 | 0.0023 |
model_herkogamy <- lm(admixture_proportion ~ herkogamy, data = clarkia)
augment(model_herkogamy)%>%
mutate(distance2hetero = pull(clarkia,distance2hetero)) %>%
ggplot(aes(x = distance2hetero, y = .resid))+
geom_point(size= 3, alpha = .7)+
geom_smooth(method = "lm") + theme(axis.text = element_text(size = 12),axis.title = element_text(size = 15))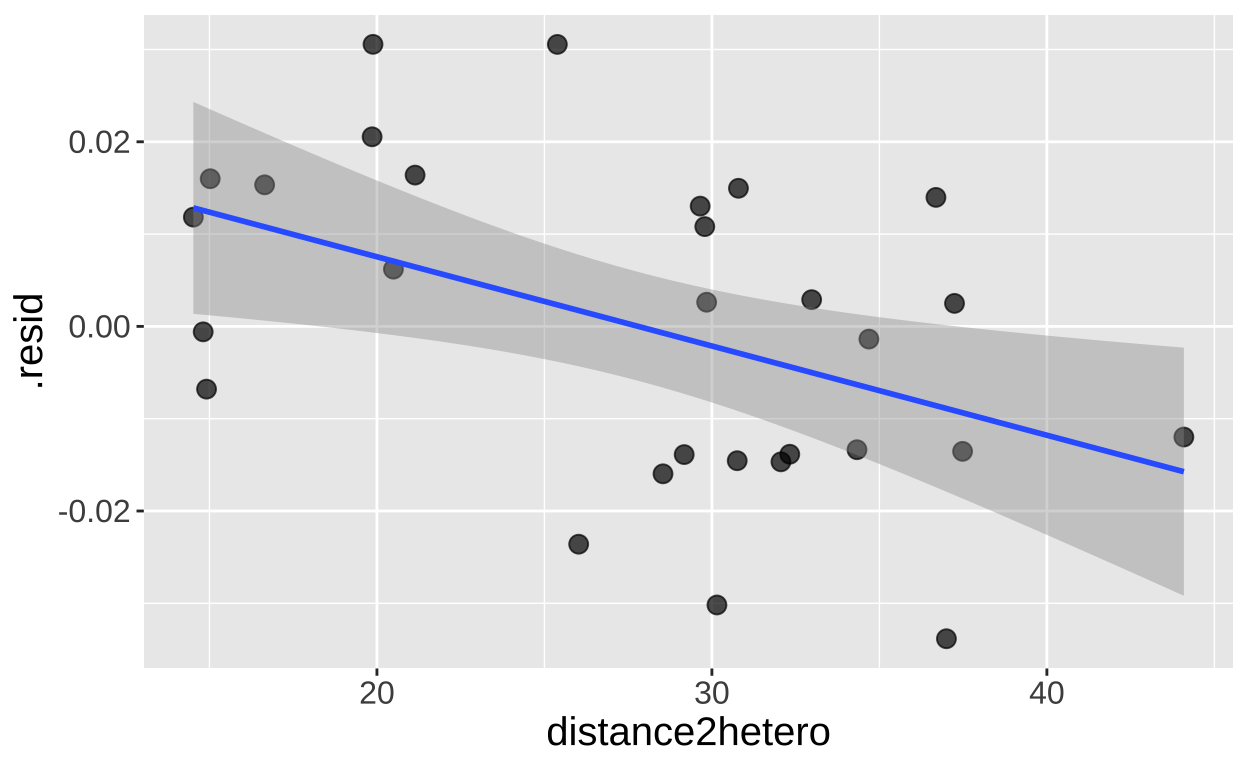
augment(model_herkogamy)%>%
mutate(distance2hetero = pull(clarkia, distance2hetero)) %>%
lm(.resid ~ distance2hetero, data = .)%>%
tidy() %>% mutate_at(2:5, round, digits =4) %>% kbl()| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0269 | 0.0105 | 2.5720 | 0.0159 |
| distance2hetero | -0.0010 | 0.0004 | -2.6752 | 0.0125 |
Building and evaluating our multiple regression model
Rather than modeling these pieces separately, multiple regression allows us to jointly model the influence of two continuous explanatory predictors on a continuous response variable. We can build this in R as we’re accustomed to:
model_dist2_herk <- lm(admixture_proportion ~ distance2hetero + herkogamy, data = clarkia)Evaulating assumptions
Multicolinearity
Let’s first check for multicollinearity. Remember, it’s difficult to interpret a multiple regression model if the explanatory variables are correlated. Fortunately, in this case, they appear to be independent! We have three peices of evidence for this:
- The correlation is weak,
- There is no obvious pattern in the plot
- The variance inflation factor (a measure of multicolinearity) is small (its about, 1 which means theres no correlation). We get a bit worried when its more than 5 and zero worried when its more than 10)!
# A tibble: 1 × 1
cor_herk_dist
<dbl>
1 -0.0448ggplot(clarkia, aes(x = distance2hetero, y = herkogamy))+
geom_point(size= 3, alpha = .7)+
geom_smooth(method = "lm") + theme(axis.text = element_text(size = 12),axis.title = element_text(size = 15))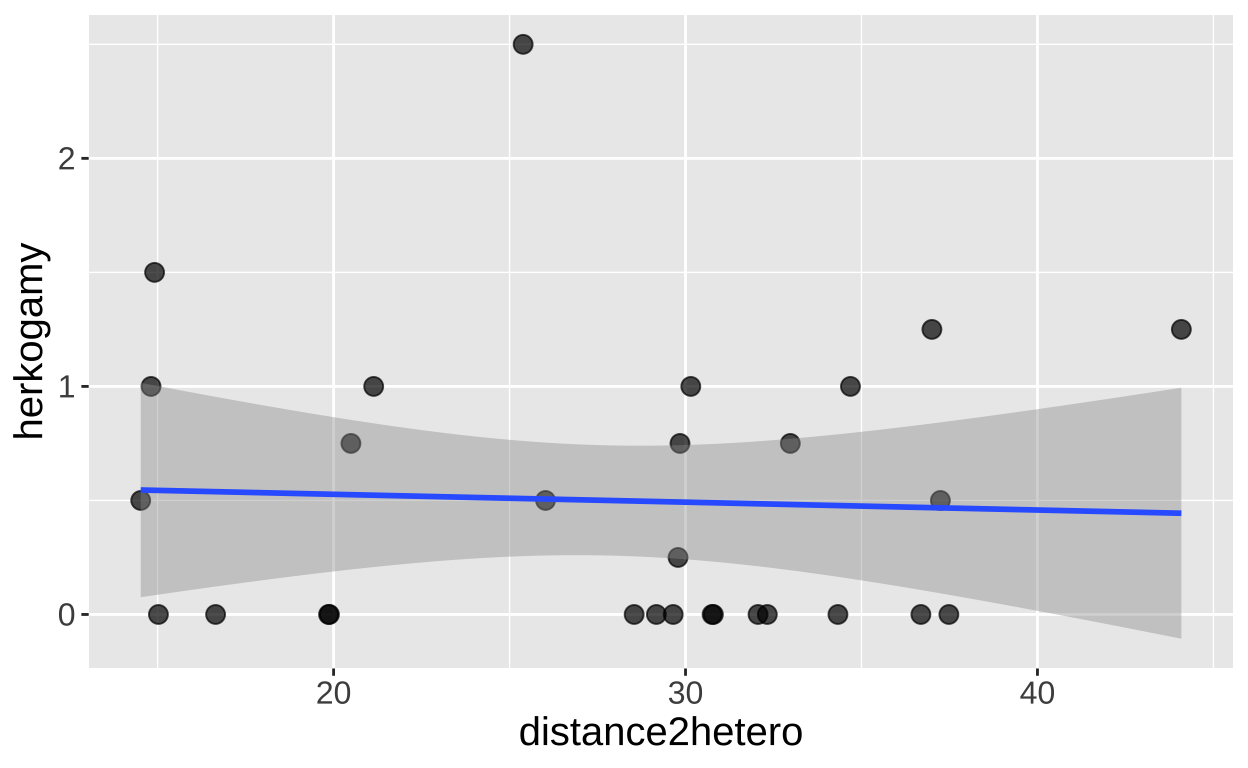
car::vif(model_dist2_herk)distance2hetero herkogamy
1.002007 1.002007 Residual variation
Our model diagnostics look pretty good. Points all largely on the qq line, the value and abosolute value of residuals are largely indpendet of predictors. Lets get to work!
autoplot(model_dist2_herk)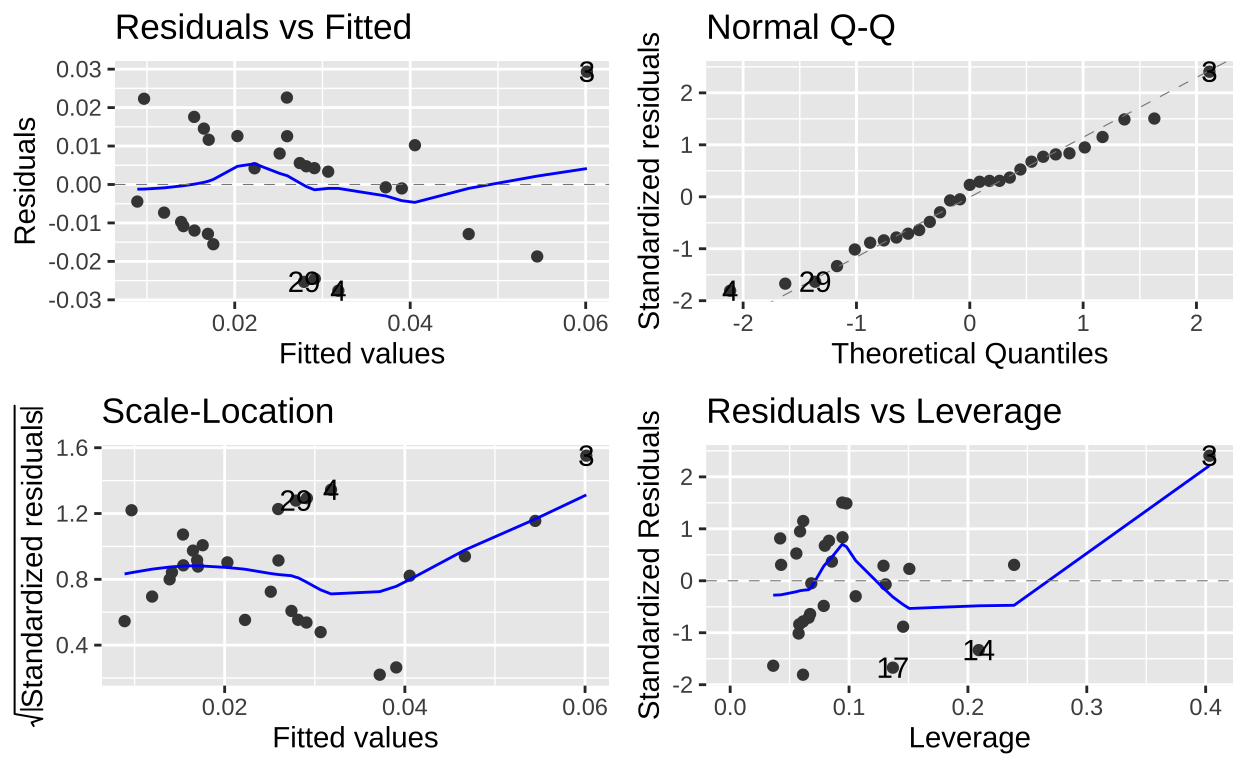
Estimation
emtrends(model_dist2_herk,var = "herkogamy")%>%
summary(infer = c(TRUE, TRUE)) %>% select(herkogamy, lower.CL, upper.CL ) %>% mutate_all(round,digits=5)%>% kbl()| herkogamy | lower.CL | upper.CL |
|---|---|---|
| 0.5 | 0.00597 | 0.02565 |
emtrends(model_dist2_herk,var = "distance2hetero")%>%
summary(infer = c(TRUE, TRUE)) %>% select(distance2hetero.trend, lower.CL, upper.CL ) %>% mutate_all(round,digits=5)%>% kbl()| distance2hetero.trend | lower.CL | upper.CL |
|---|---|---|
| -0.00097 | -0.00173 | -0.00021 |
Types of sums of squares.
By default, the anova() function uses Type I Sums of Squares, which we introduced earlier. Remember, with Type I Sums of Squares, you calculate the sums of squares for the first predictor by fitting a model with only that predictor. Then, to find the sums of squares for the second predictor, you subtract the sums of squares from the first predictor’s model from the sums of squares of a model including both predictors. This means the order in which predictors are entered into the model affects the results. I demonstarted this below
Analysis of Variance Table
Response: admixture_proportion
Df Sum Sq Mean Sq F value Pr(>F)
distance2hetero 1 0.0019218 0.00192177 7.7233 0.009991 **
herkogamy 1 0.0027128 0.00271278 10.9023 0.002796 **
Residuals 26 0.0064695 0.00024883
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analysis of Variance Table
Response: admixture_proportion
Df Sum Sq Mean Sq F value Pr(>F)
herkogamy 1 0.0029154 0.00291536 11.7164 0.002062 **
distance2hetero 1 0.0017192 0.00171919 6.9092 0.014204 *
Residuals 26 0.0064695 0.00024883
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1This ordering is ok if we’re dealing with a covariate we don’t care much about. However, it’s not ideal for testing interesting biological models, as we don’t want our answers to depdne on the order things went into lm().
In contrast, Type II Sums of Squares calculates the sums of squares for each factor after accounting for the other factor. It’s as if both factors are treated as the “second” predictor in a Type I Sums of Squares model. That is, each factor’s effect is measured independently of the order in which they are entered. We can calculate type II sums of squares with the Anova() function in the cars package:
Anova Table (Type II tests)
Response: admixture_proportion
Sum Sq Df F value Pr(>F)
distance2hetero 0.0017192 1 6.9092 0.014204 *
herkogamy 0.0027128 1 10.9023 0.002796 **
Residuals 0.0064695 26
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Note that our entries both look like they did when they were the second thing in a Type I sums of squares model.
Visulaizing multiple regression: Added Variable plots
Visualizing multivariate relationships can be challenging. Above, we explored a few approaches to address this. For example, in our first plot, we placed the response variable (admixture proportion) on the y-axis, one explanatory variable on the x-axis, and represented another explanatory variable using color. However, this approach can be difficult to interpret. To provide a more comprehensive view, we used a ggpairs plot to display all combinations of pairwise relationships, as well as residual plots.
Here, I introduce the added variable plot (AV plot). An AV plot is similar to a residual plot. On the y-axis, it shows the residuals from a model where the response is predicted by all variables except the focal predictor (the explanatory variable of interest). The x-axis displays the residuals of the focal predictor after it has been modeled as a function of all other predictors. This plot allows us to visualize the unique contribution of the focal predictor to the response, independent of the other variables in the model.
a <- tibble(
resid_y = lm(admixture_proportion ~ herkogamy, data = clarkia) %>% augment() %>% pull(.resid),
resid_x = lm(distance2hetero ~ herkogamy, data = clarkia) %>% augment() %>% pull(.resid))%>%
ggplot(aes(x = resid_x, y = resid_y))+
geom_point()+
labs(x = "Distance to hetero | others", y = "Admixture proportion | others")+
geom_smooth(method = "lm")
b <- tibble(
resid_y = lm(admixture_proportion ~ distance2hetero, data = clarkia) %>% augment() %>% pull(.resid),
resid_x = lm(herkogamy ~ distance2hetero, data = clarkia) %>% augment() %>% pull(.resid))%>%
ggplot(aes(x = resid_x, y = resid_y))+
geom_point()+
labs(x = "Herkogamy | others", y = "Admixture proportion | others")+
geom_smooth(method = "lm")
a + b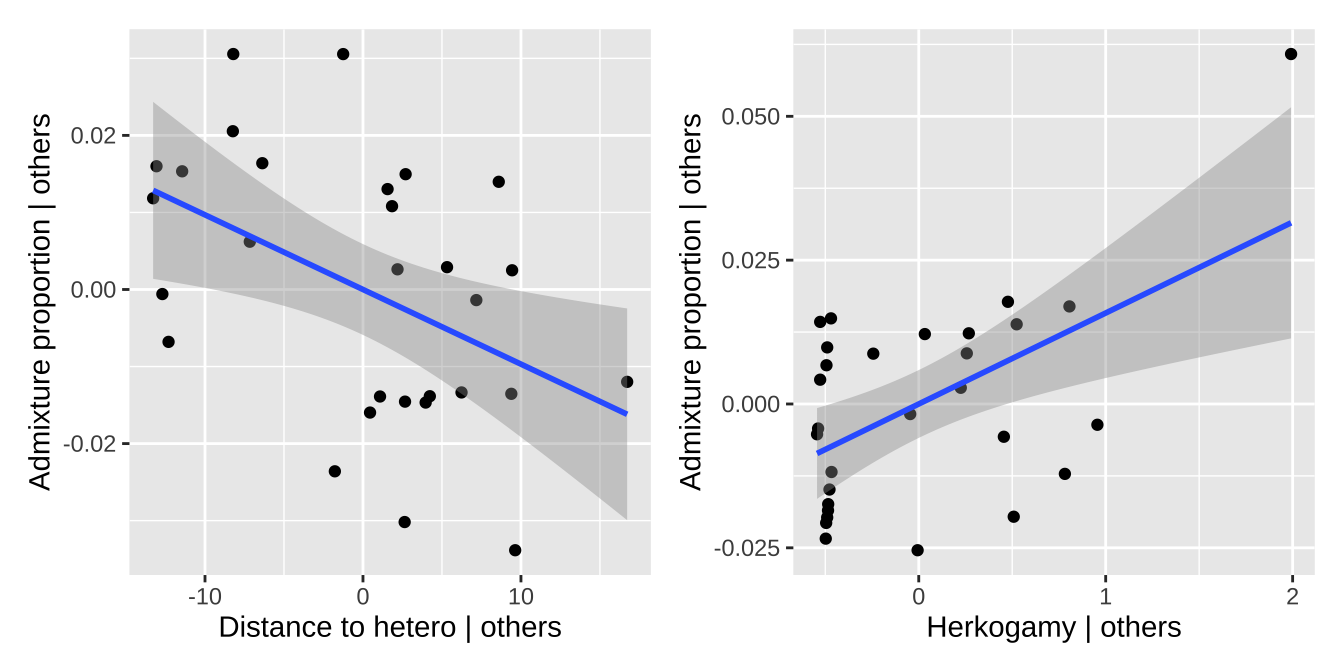
Comparing coefficients.
| variable | lower.CL | estimate | upper.CL |
|---|---|---|---|
| distance2hetero | -0.00173 | -0.00097 | -0.00021 |
| herkogamy | 0.00597 | 0.01581 | 0.02565 |
Looking at our model coefficients, we see that the admixture proportion changes much more rapidly with herkogamy than it does with distance to a heterosubspecific. Does this mean that distance to heterosubspecifics is less important? Not necessarily! These variables have different ranges, variances, etc. A standardized regression coefficient allows for an apples-to-apples comparison. We can find this by z-transforming all x and y variables. You can think of this value as a correlation—in fact, it’s the correlation when there is only one explanatory variable.
Now we see that the effects are quite similar!
# first we write our own function to z-transform
zTransform <- function(X){(X-mean(X,na.rm = TRUE)) / sd(X,na.rm = TRUE) }
clarkia%>%
mutate_all(zTransform) %>%
lm(admixture_proportion ~ herkogamy + distance2hetero, data = .) %>% coef()%>% round(digits=3)%>%kable()| x | |
|---|---|
| (Intercept) | 0.000 |
| herkogamy | 0.495 |
| distance2hetero | -0.394 |
Conclusion
We find more admixture in parvilora plants closer to a hetero-subspecific, and more admixture in these plants that have more distance between their anthers and stigmas. There are numerous potential causal interpretations of these trends.
Dealing with Multicollinearity
What should you do if you’re worried about multicollinearity? Here are a few potential strategies:
Remove or Combine Variables: If two variables are largely redundant, you can remove one or combine them in some way. For example, the
herkogamyvalue in the example above is actually the average herkogamy across a plant’s first two flowers.PCA or Other Ordination Techniques: Principal Component Analysis (PCA) aims to summarize multivariate data into combinations of variables that best explain the variability in the dataset. Principal component regression finds principal components of the predictor variables and uses the first few components as explanatory variables. This approach is effective because principal components are orthogonal. However, presenting and interpreting results form a principal components regression can be challenging.
Run Models with Various Combinations of Parameters: Experiment with leaving out different predictors. How stable are your estimates and p-values as you remove or combine variables? If the results are robust to the inclusion or exclusion of certain variables, we can feel better about our model.
Quiz
Figure 5: Quiz on the multiple regression here