Motivating scenarios: You want to understand the intellectual basis for a foundation challenge in statistics.
Learning goals: By the end of this chapter you should be able to:
- Differentiate between a parameter and and an estimate.
- Describe the different ways sampling can go wrong (sampling bias, nonindependence and sampling error) that make estimates deviate from parameters, and how to spot and protect against them.
- Describe the sampling distribution and why it is useful.
- Use
Rto build a sampling distribution from population data.
- Describe the standard error.
- Understand how sample size influences sample estimates.
Populations have parameters
The palmerpenguins dataset we’ve been looking at consists of 344 penguins of three species. In the sample we have 152 Adelie penguins, 68 Chinstrap penguins, and 124 Gentoo penguins. For now, lets pretend this is a census – i.e. let us pretend this represents all penguins on these three islands. In this census, we see that \(\frac{68}{344} = 19.8%\)of this population is are Chinstrap penguins.
In a real way the calculation above is a population parameter it is the true value of the proportion of penguins in this data set that are chinstrap (although this is not a parameter for the entire world, it is for this example).
In frequentist statistics, population parameters are the TRUTH or the world out there as it really is, either from a population census, or from some process which will generate data with certain characteristics (e.g. flipping a coin, recombining chromosomes, responding to a drug etc…). In our example, the entire census data is presented in the table below (Figure 1).
Figure 1: The entire population of our penguins data set (presented in random order).
Estimate population parameters by sampling
It is usually too much work, costs too much money, takes too much time etc. etc. to characterize an entire population and calculate its parameters.
So we take estimates from a sample of the population. This is relatively easy to do in R if we already have a population, we can use the slice_sample() function, with the arguments being the tibble of interest, n the size of our sample. The sample of size 30 in the table below contains 6 Chinstrap penguins. So 20% of this sample are Chinstrap penguins – a difference of about 0.23% from the true population parameter of 19.8%. Figure ?? compares the census proportion of each species (i.e. the data we have - in lighter colors) to a random sample of thirty penguins from our data (darker colors).
penguins_sample <- slice_sample(penguins, n = 30, replace = FALSE) Figure 2: A sample of size 30 from our larger penguins dataset.
bind_rows(dplyr::mutate(penguins, data = "population (true parameter)"),
dplyr::mutate(penguins_sample, data = "sample (parameter estimate)")) %>%
group_by(data, species) %>%
tally()%>%
mutate(propotion = n/sum(n)) %>%
ggplot(aes(y = data, x = propotion, fill = species, alpha= data))+
geom_col(show.legend = FALSE)+
facet_wrap(~species,ncol=1)+
theme(strip.text = element_text(size = 15),axis.text = element_text(size = 15),axis.title = element_text(size = 15))+
scale_alpha_manual(values = c(.3,1))+
scale_x_continuous(limits = c(0,1), breaks = c(0,.5,1), labels = c("0","1/2","1"))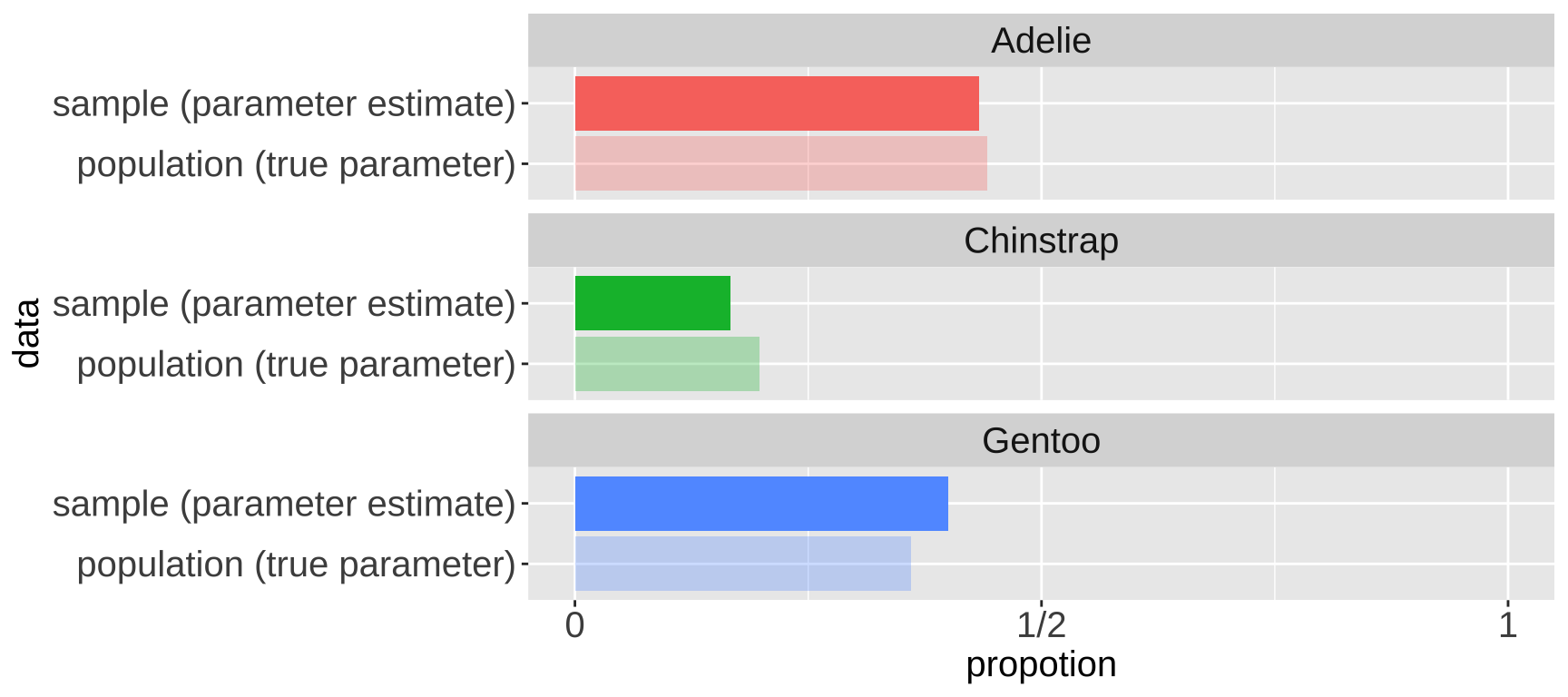
Figure 3: Comparing the proportion of each species in the sample of size 30 (i.e.e the sample estimate) to its actual parameter value in the census (i.e. the true proportion, light colors)
Review of sampling
Of course, if we already had a well characterized population, there would be no need to sample – we would just know actual parameters, and there would be no need to do statistics. But this is rarely feasible or a good idea, and we’re therefore stuck taking samples and doing statistics.
As such, being able to imagine the process of sampling – how we sample, what can go wrong in sampling is perhaps the most important part of being good at statistics. I recommend walking around and imagining sampling in your free time.
(Avoiding) Sampling Bias
. Accompanying text: *fMRI testing showed that subjects who dont agree to participate are much more likely to escape from the machine mid-scan.*](https://imgs.xkcd.com/comics/selection_effect.png)
Figure 4: Example of sampling bias from xkcd. Accompanying text: fMRI testing showed that subjects who dont agree to participate are much more likely to escape from the machine mid-scan.
Say we were interested to know if Chinstrap penguins in our dataset have shorter or longer bills than the other penguin species in our dataset. We could take our 30 individuals from our randomly generated sample above and take estimates for all three species. If all species’ estimates are unbiased, and individuals are sampled independently, we only have to deal with sampling error, discussed below. But maybe we cannot randomly collect penguins - then we have to deal with bias and non-independence in our sampling. This is why polling is so hard.
But it’s often even worse – we don’t have a list of possible subject to pick from at random – so what do we do? Say we want a good poll for the presidential election in order to predict the outcome. Do we build on online survey? Try calling people? Go to the campus cafeteria? You can see that each of these could introduce some deviation between the true population parameters and the sample estimate. This deviation is called sampling bias and it can ruin all of the fancy statistical tricks we use to recognize sampling error.
Top be more specific, our dataset covered three islands. And if we say, just sampled from Drem island, we would estimate that 68 of 124, (aka 55%) of penguins are Chinstrap penguins
# A tibble: 2 × 2
species n
<fct> <int>
1 Adelie 56
2 Chinstrap 68When designing a study, do everything you can to eliminate sampling bias, and when doing any analysis yourself or considering anyone else’s, always consider how sampling bias could mislead us.

(Avoiding) non-independence of Samples
One last important consideration of sampling is the independence of samples.
- Samples are independent if sampling one individual does not change the probability of sampling another.
- Samples are dependent (also called non-independent) if sampling one individual changes the probability of sampling another.
Say we are interested to estimate the proportion of penguins that are Chinstrap. If we go to an (imaginary) island where all species are on average, equally likely to hang out, but individuals of each species tend to be near one another. We then find a place with somepenguins and start counting. In this case our sample will be dependent – once we find our first penguin, others (nearby) are more likelyto be of this species then they would be if we randomly picked another spot to sample.
Near the end of the term, we’ll consider ways of accounting for non-independence. For now, know that dependence changes the process of sampling and requires us to build more complex models.
When designing an experiment, or considering someone else’s, we therefore worry about Pseudo-replication the name for non-independent replication (See Fig. 5).
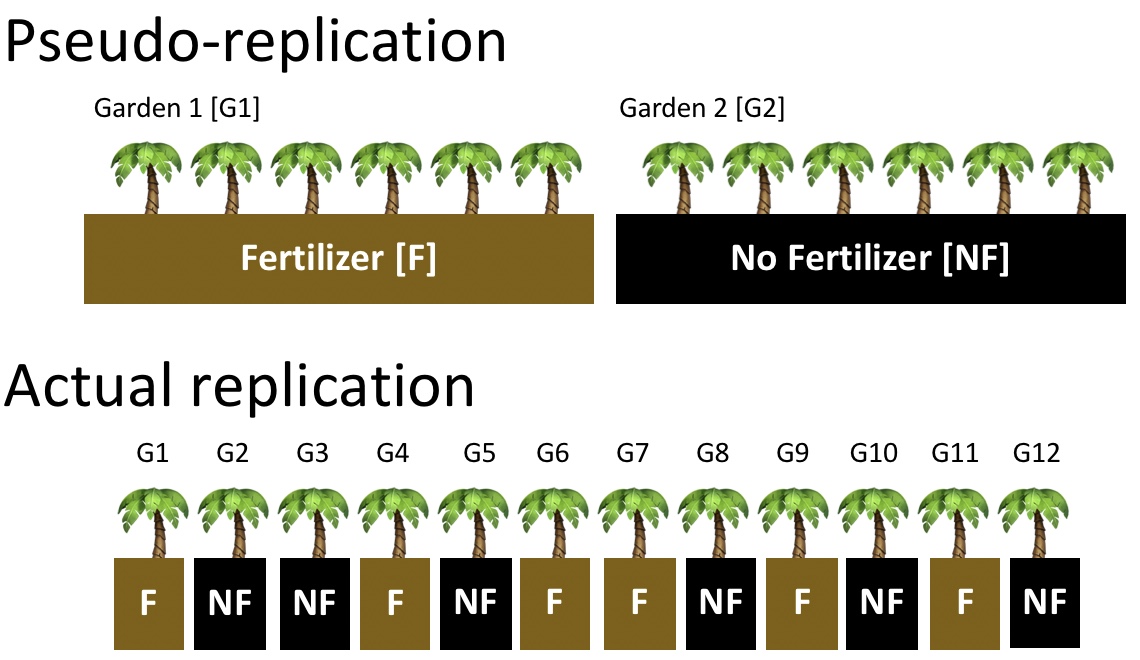
Figure 5: Comparing pseudo-replication (top) to independent replication (bottom). With pseudo-replication the effect of our experimental intervention (in this case fertilizer), is tied up with differences between environments unrelated to treatment (in this case, differences between gardens). Separating treatment and garden, and randomly placing treatments onto garden removes this issue.

There is no avoiding sampling Error
Estimates from samples will differ from population parameters by chance. This is called sampling error (Introduced previously). But make no mistake – sampling error cannot be avoided. We have just seen an example of sampling error when our estimate of the proportion faculty at the College of the Atlantic deviated from the true parameter.
Larger samples and more exacting measures can reduce sampling error, but it will always exist because we take our samples by chance. In fact, I would call it the rule of sampling rather than sampling error.
All of the material in the rest of this chapter – and about a half of the rest of this term – concerns how to deal with the law of sampling error. Sampling error is the obsession of many statistical methods.
The sampling distribution
OK, say you collected data for a very good study, and you’re very excited about it (as well you should be!). 🎉 CONGRATS!🎉 Stand in awe of yourself and your data – data is awesome and it is how we understand the world.
But then get to thinking. We know that the law of sampling error means that estimates from our data will differ from the truth by chance. So, we start to imagine ‘’what could other outcomes have been if the fates blew slightly differently?’’
The sampling distribution is our tool for accessing the alternate realities that could have been. The sampling distribution is a histogram of estimates we would get if we took a random sample of size \(n\) repeatedly. By considering the sampling distribution we recognize the potential spread of our estimate.
I keep saying how important sampling and the sampling distribution is. So, when, why, and how do we use it in statistics??? There are two main ways.
First, when we make an estimate from a sample, we build a sampling distribution around this estimate to describe uncertainty in this estimate (See the coming Section on Uncertainty).
Second, in null hypotheses significance testing (See the coming section on hypothesis testing) we compare our statistics to its sampling distribution under the null, to see how readily it could have been caused by sampling error.
Thus the sampling distribution plays a key role in two of the major goals of statics - estimation and hypothesis testing.
Wrapping your head around the sampling distribution is critical to understanding our goals in this term. It requires imagination and creativity. That is because we almost never have or can make an actual sampling distribution (because we don’t have an actual population). Rather we have to imagine what it would look like under some model given our single sample. That is we recognize that we have only one sample, and will not take another, but we can imagine what other estimates from another go at sampling would look like. Watch the first five minutes of the video below for the best explanation of the sampling distribution I have come across.
Figure 6: Watch the first 5 minutes of this description of the sampling distribution. Burn this into your brain.
Building a sampling distribution
So, imagining a sampling distribution is very useful. But we need something more concrete than our imagination. How do we actually generate a useful sampling distribution???
Building a sampling distribution by repeatedly sampling
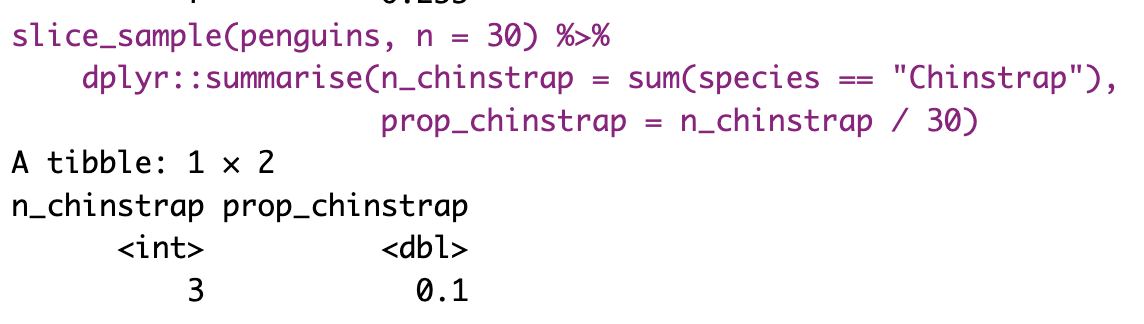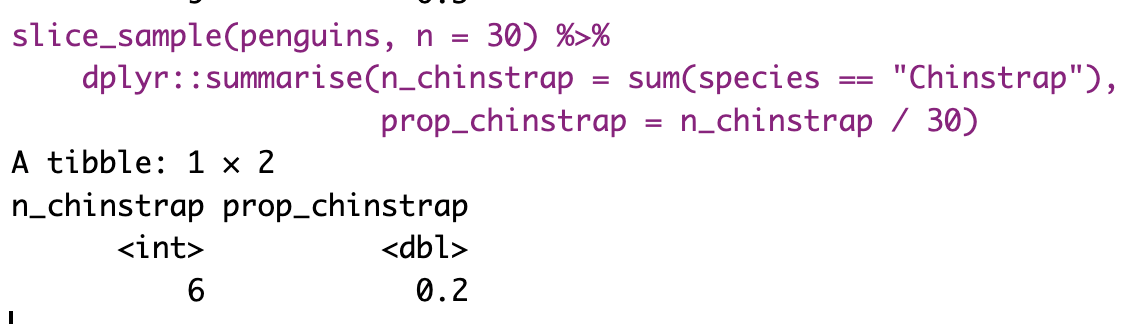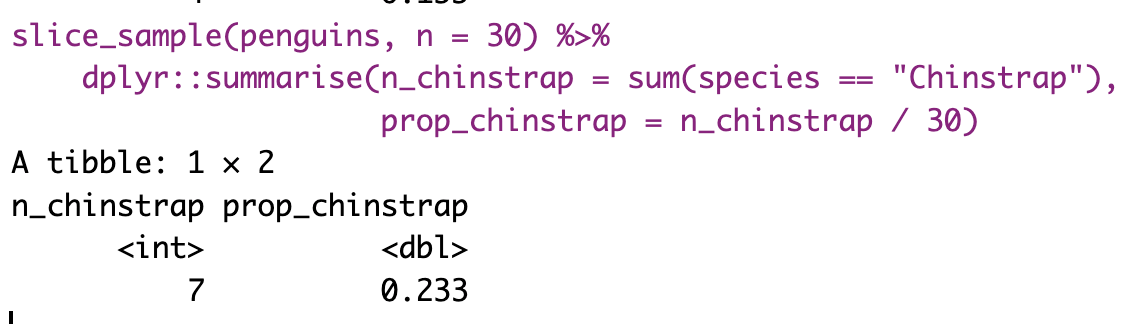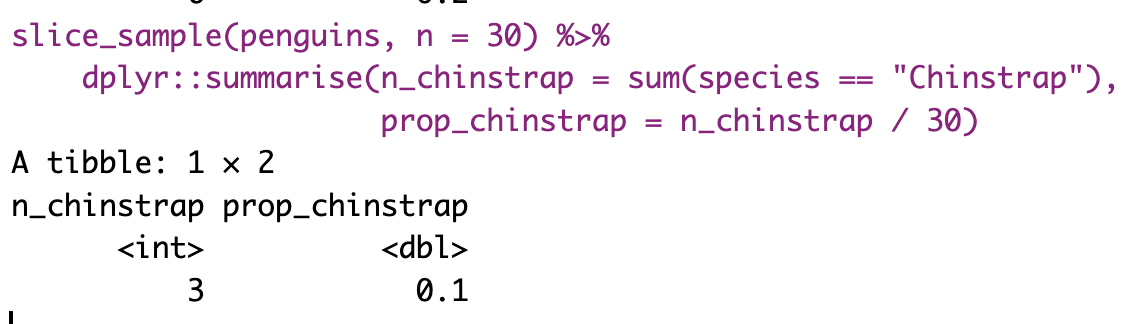
The most conceptually straightforward way to generate a sampling distribution is to take a bunch of random samples from our population of interest. Below, I just kept repeating our code a bunch of time, so you get a sense of what we are doing.
However, that is a pain to save and record etc, so I will show you how to have R do this for us below.
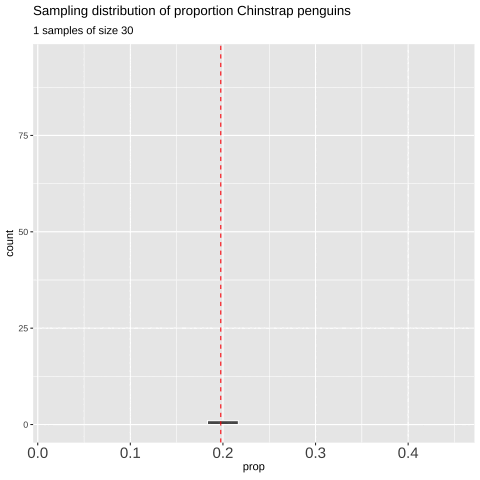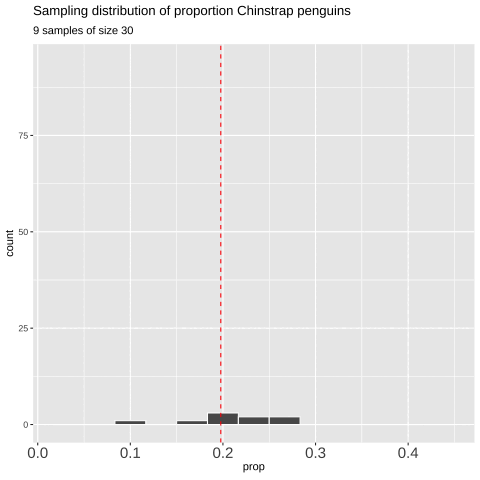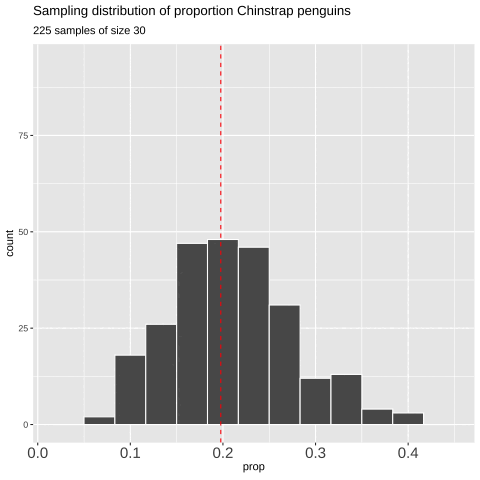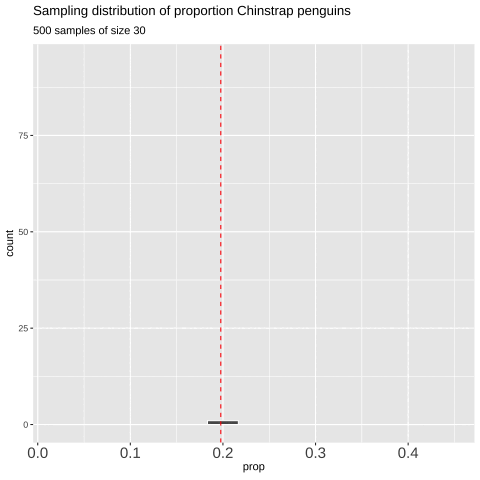
Figure 7: Shows the different estimates of the proportion of Chinstrap penguins with an unbiased an independent sample of size 30 – building a histogram of sample estimates if we were to sample a bunch. This histogram is known as the sampling distribution.
We can make a sampling distribution by resampling from a population by replicating our code a bunch of times with the replicate() function. For mundane formatting reasons, we need to set the argument simplify = TRUE inside of replicate() and pipe this output to the bind_rows() function. The code below shows how we can generate the data for Figure 7.
While this approach is conceptually straightforward it is also silly and not useful in practice – there is no reason to characterize a whole population and then resample from it to make an estimate. More often, we have an estimate from a single sample and need some way to consider the sampling distribution.
Building a sampling distribution by simulation
If we have some sense (or hypothesis) of how our population might behave, we can simulate data from it. Like most programming languages, R allows for incredibly complex simulations (I’ve simulated whole genomes), but for now, let’s simulate the process of sampling with the sample() function.
For example, we can generate a sample from a population in which I hypothesized that one third of the penguins are Chinstrap penguins (i.e. all species are equally common in our dataset).
and then find the proportion that are Chinstrap.
mean(my_sample == "Chinstrap")[1] 0.3We could do this a bunch of times by simulating a bunch of samples (n_samples) each of size sample_size. The R code below provides one way to do this.
n_samples <- 500
sample_size <- 30
simulated_data <- tibble(replicate = rep(1:n_samples, each = sample_size),
# Here we make a bunch of replicate ids numbered
# 1:n.reps, repeating each id sample.size times
species = sample(c("Chinstrap","Other penguin species"),
size = sample_size * n_samples,
prob = c(1/3,2/3),
replace = TRUE) )
# Here, we simulate a bunch (sample_size * n_reps) of observations,
# assigning the first sample.size observations to replicate 1,
# the second sample.size observations to replicate 2 etc. etc... We can then make an estimate from each replicate using the group_by() and summarise() functions we encountered previously.

Building a sampling distribution by math
We can also use math tricks to build a sampling distribution. Historically, simulation was impractical because computers didn’t exist, and then where too expensive, or too slow, so mathematical sampling distributions were how stats was done for a long time. Even now because simulation can take a bunch of computer time, and because it too is influenced by chance, a majority of statistical approaches use mathematical sampling distributions.
We will make use of a few classic sampling distribution over this course, including the \(F\), \(t\), \(\chi^2\), binomial, and \(z\) distributions. For now, recognize that these distributions are simply mathematically derived sampling distributions for different models. They aren’t particularly scary or special.
The Standard Error
The standard error, which equals the standard deviation of the sampling distribution, describes the expected variability due to sampling error of a sample from a population. Recall from our introduction to summarizing the width of data, that the sample standard deviation, \(s\) is the square root of the average squared difference between a value and the mean (\(s = \sqrt{\frac{\Sigma (x_i - \overline{x})^2}{n-1}}\)), where we divide by \(n-1\) instead of \(n\) to get an unbiased estimate. For our calculation here, \(x_i\) represents the estimated mean of the \(i^{th}\) sample, \(\overline{x}\) is the population mean (68/344 for our proportion Chinstrap example), and \(n\) is the number of replicates (n_samples in our code above).
The standard error is a critical description of uncertainty in an estimate (See the next section on uncertainty). If we have a sampling distribution, we can calculate it as follows.
# A tibble: 1 × 1
standard.error
<dbl>
1 0.0728Minimizing sampling error
We cannot eliminate sampling error, but we can do things to decrease it. Here are two ways we can reduce sampling error:
Decrease the standard deviation in a sample. We only have so much control over this, because nature is variable, but more precise measurements, more homogeneous experimental conditions, and the like can decrease the variability in a sample.
Increase the sample size. As the sample size increases, our sample estimate gets closer and closer to the true population parameter. This is known as the law of large numbers. Remember that changing the sample size will not decrease the variability in our sample, it will simply decrease the expected difference between the sample estimate and the population mean.
The webapp (Figure 8) from Whitlock and Schluter (2020) below allows us to simulate a sampling distribution from a normal distribution (we return to a normal distribution later). Use it to explore how sample size (\(n\)) and variability (population standard deviation, \(\sigma\)) influence the extent of sampling error. To do so,
- First click the sample one individual button a few times. When you get used to that,
- Click complete the sample of ten, and then calculate mean. Repeat that a few times until you’re used to it.
- Then click means for many samples and try to interpret the output.
- Next, click show sampling distribution.
- Finally, pick different combinations of \(n\) and \(\sigma\) – increasing and decreasing them one at a time or together and go through steps 1-4 until you get a sense for how they impact the width of the sampling distribution.
Figure 8: Webapp from Whitlock and Schluter (2020) showing the process of sampling and the sampling distribution. Find it on their website.
Be wary of exceptional results from small samples
Because sampling error is most pronounced in a small sample, estimates from small samples can mislead us. Figure 9 compares the sampling distributions for the proportion of Chinstrap penguins in samples of size five, thirty, and one hundred. About one third of samples of size of five have exactly zero Chinstrap penguins. So seeing no Chinstrap penguins in this sample would be unsurprising, but facilitates misinterpretation. Imagine the headlines
“Chinstrap penguins have disappeared, and may be extinct!…”
The very same sampling procedure from that same population (with a sample size of five) could occasionally result in an extreme proportion of cases in with more than half of the penguins are Chinstrap penguins (this occurs in about six percent of samples of size five). A sample like this would yield a quite different headline.
“Chinstrap penguins on the rise – could they be replacing oteher penguin species>”
A sample of size thirty is much less likely to mislead – it will only yield a sample with zero ora majority of Chinstrap penguins about one in one thousand times.
The numbers I gave above are correct and scary. But it gets worse – since unexceptional numbers are hardly worth reporting (illustrated by the light grey coloring of unexceptional values in Figure 9), so we’ll rarely see accurate headlines like this.
“A survey of penguins shows an unremrable proportionof three well-studied penguin species…”
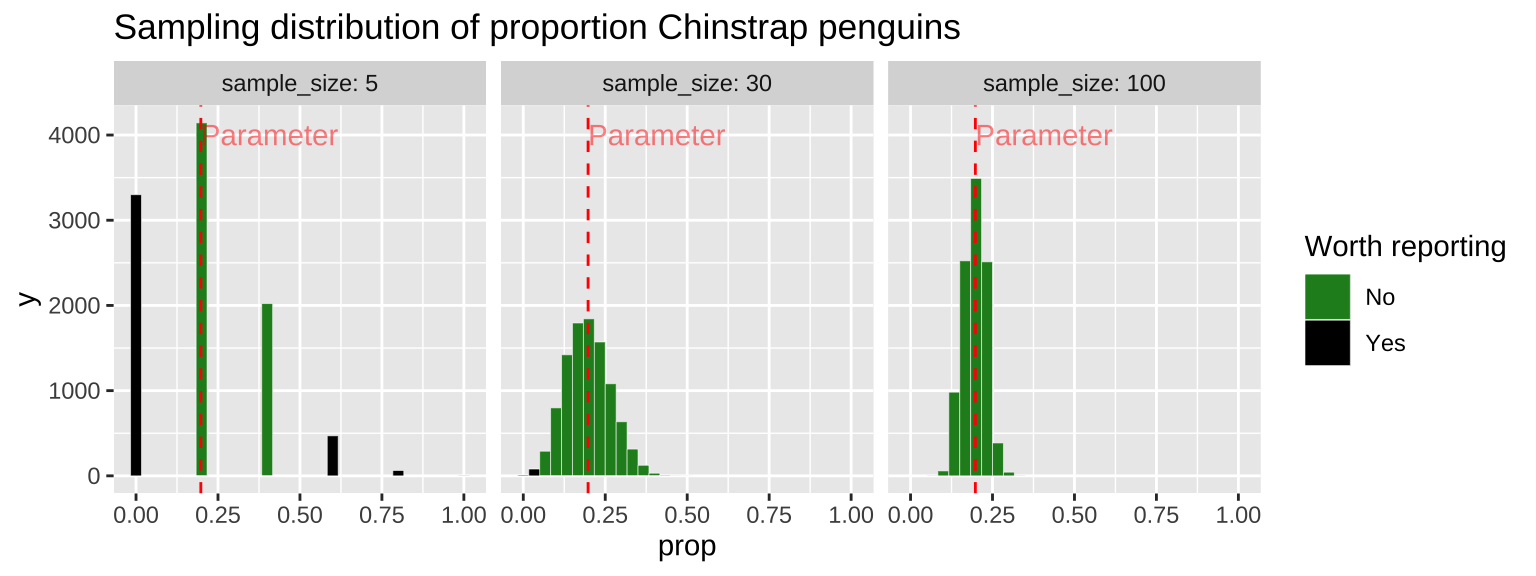
Figure 9: Comparing the sampling distribution of faculty proportion in samples of size five, thirty, and one hundred. The true population proportion is 0.198. Bars are colored by if they are likely to be reported (less than 5% or more than 39%), with unremarkable observations in dark green.
The take home message here is whenever you see some exceptional claim be sure to look into the sample size, and measures of uncertainty, which we discuss in next chapter. For a nice discussion check out this optional reading, The most dangerous equation (Wainer 2007).
Small samples, overestimation, and the file drawer problem
Say you have a new and exciting idea – say a pharmaceutical intervention to cure a deadly cancer. Before you do a huge study, you may want to do a small pilot project with a limited sample size – as this would be necessary before getting a bunch of money and permits and allotting time etc…
What if you found a super cool result?? – the drug worked even better than you initially hoped? You would probably jump up and down and shout it from the rooftops – put out a press release etc…
What if you found something very subtle?? – the drug might have helped, but you can’t really tell. Maybe you’d keep working on it, but more likely you would drop it and move on to a more promising target.
After reading this Section, you know that these two outcomes could happen for two drugs with the exact same effect (see Figure 9). This combination of sampling and human nature has the unfortunate consequence that reported results are often biased towards extreme outcomes. This issue, known as the file drawer problem (because underwhelming results are kept in a drawer somewhere until some mythical day when we have time and energy to share them), means that most published results are overestimated, modest effects are under-reported, and follow up studies tend show weaker effects than early studies. Importantly, this happens even if all experiments themselves are performed without bias, and insisting on statistical significance does not help.
Quiz
Figure 10: The accompanying quiz link
Definitions, Notation, Equations, and Useful functions
Terms
Newly introduced terms
Standard error A measure of how far we expect our estimate to stray from the true population parameter. We quantify this as the standard deviation of the sampling distribution.
Pseudo-replication Analyzing non-independent samples as if they were independent. This results in misleading sample sizes and tarnishes statistical procedures.Review of terms from the introduction to statistics
Many of the concepts discussed in this chapter were first presented in the Introduction to Statistics and have been revisited in greater detail in this chapter.
Sample: A subset of a population – individuals we measure.
Parameter: A true measure of a population.
Estimate: A guess at a parameter that made from a finite sample. Sampling error: A deviation between parameter and estimate attributable to the finite process of sampling.
Sampling bias: A deviation between parameter and estimate attributable to non representative sampling.
Independence: Samples are independent if the probability that one individual is studied is unrelated to the probability that any other individual is studied.
Functions for sampling in R
sample(x = , size = , replace = , prob = ): Generate a sample of size size, from a vector x, with (replace = TRUE) or without (replacement = FALSE) replacement. By default the size is the length of x, sampling occurs without replacement and probabilities are equal. Change these defaults by specifying a value for the argument. For example, to have unequal sampling probabilities, include a vector of length x, in which the \(i^{th}\) entry describes the relative probability of sampling the \(i^{th}\) value in x.
slice_sample(.data, ..., n, prop, weight_by = NULL, replace = FALSE): Generate a sample of size n, from a tibble .data, with (replace = TRUE) or without (replacement = FALSE) replacement. All arguments are the same as in sample() except weight replaces prob, and .data replaces x. slice_sample() is a function in the dplyr package, which is loaded with tidyverse.