13 Transforming data

Anyone regularly working with data is aware that transforming data (aka. “data munging” or “data wrangling”) is an essential pre-requisite for any successful data analysis.

The task of transforming data can be further decomposed into reducing or reshaping data. Our main focus in the current chapter lies on reducing data (by creating chains of functions that allow answering questions about the contents of a dataset). By contrast, the next Chapter 14 will primarily focus on reshaping data (by turning “messy” into “tidy” tables).

The key sections and topics (and corresponding R packages) of this chapter are:

• Section 13.2: The pipe operator from magrittr (Bache & Wickham, 2022)

• Section 13.3: Transforming tables with dplyr (Wickham, François, et al., 2023)

Both these sections and packages are designed for manipulating data structures (mostly vectors or tables) into other data structures (more vectors or tables). Although transforming data can be viewed as a challenge and a task in itself, our primary goal usually consists in gaining insights into the contents of our data.

Preparation

Recommended readings for this chapter include

• Chapter 3: Transforming data of the ds4psy book (Neth, 2023a)

• Chapter 5: Data transformation of the r4ds book (Wickham & Grolemund, 2017)

Preflections

Before reading, please take some time to reflect upon the following questions:

• Assuming we had all the data required for answering our question, which additional obstacles would we face?

• In which data structures are the answers to our data-related questions represented?

• Do answers to our data-related questions always contain the entire data? Or do we typically select and reduce data, so that it becomes impossible to reconstruct the data from our answers?

13.1 Introduction

In Section 1.2.5, we introduced the notion of ecological rationality and quoted Herbert A. Simon:

Solving a problem simply means representing it so as to make the solution transparent.
(Simon, 1981, p. 153)

The deep wisdom expressed by this quote also applies to the efforts of data science in general, and to the task of transforming data in particular. In both cases, we aim and hope for some answer or insight that may be hidden in the data. If we succeed in re-representing the data in a way that makes this solution evident, our original problem disappears.

Transforming data is probably the single most important skill of data scientists. While flashy visualizations or fancy statistical models may be the most obvious fruits of our efforts, our skills for transforming data typically lead a more clandestine and silent life. But just as a group of star actors do not yet make a great movie, any successful data science project depends on solid data transformation skills.

One reason for the lack of attention to data transformation is that tutorials on statistical or visualization functions typically use data that just happens to be in the right format. While this conveniently allows demonstrating the power of those tools, it obscures the need and efforts required for bringing data into this form.

Any student of a foreign language will attest that understanding or repeating a well-formed sentence is easier than producing it. Thus, to become fluent in data science, we must be able to recognize different forms of data and learn how we can transform data into them. Ideally, we will eventually become so proficient in these skills that they will become automatic and invisible again. Thus, expert data scientists often fail to be aware of the difficulty that simple data transformation problems provide to novices. For them, solving a problem of transforming data simply means representing it so as to make the solution transparent.

As we have seen for previous challenges, our skills of transforming data are boosted by mastering a mix of concepts and tools.

13.1.1 Key concepts

In addition to introducing two popular tidyverse packages, this chapter introduces some terminology for talking about data transformations:

• The current section will distinguish between reshaping and reducing data as two types of data transformation;

• Key concepts of Section 13.2 are piping and the use of linear pipes in R (using the pipe operator %>% of the magrittr package or the base R operator |>);

• Section 13.3 introduces functions to filter, select, and mutate variables, and group and summarize data (from the dplyr package). Each function denotes a corresponding concept.

13.1.2 Reshaping vs. reducing data

Data transformations and the corresponding functions can be classified into two general types:

1. Reshaping operations modify the shape or structure of data without changing its contents. A motivation for re-shaping data is that some shapes are more suitable for further analysis than others. Typical examples for reshaping data include transforming the values of a vector into an array or matrix, or re-arranging the rows or columns of a table. (A particular form of tabular data will be described as tidy in Chapter 14 on Tidying data.)

2. Reducing operations are data transformations that typically modify both the shape and content of data. Examples of data reductions include sampling values from a population, describing a set of values by some measure (e.g., its mean or median), or computing some summary measure out of a set of values (e.g., to learn about a test’s sensitivity or positive predictive value).

Importantly, reshaping data is less invasive than reducing data. Whereas reshaping operations can be reversed, reducing data usually goes beyond mere “trans-formation” by being uni-directional: We typically cannot reconstruct the original data from reduced data.

13.1.3 Practice: Reshape or reduce?

Assuming the following vectors v and a:

v <- 1:9
a <- sample(c("A", "B", "C"), 10, replace = TRUE)

do the following operations reshape or reduce these data structures? Why?

Hint: Evaluate the expressions in order to see their results.

matrix(v, nrow = 3)
mean(v)
data.frame(nr = v, freq = v) %>% 
  group_by(nr) %>%
  count()

rev(a)
table(a)
a == "A"

Having distinguished between two types of transforming data, we can ask:

• Which data structures are being transformed?
• Which data structures are they being transformed into?

While both types of data transformations can be demonstrated with vectors, we mostly operate on data tables. Working with a table (as inputs to functions) typically yields new tables (as outputs of functions). This is where the pipe operator %>% from the magrittr package (Bache & Wickham, 2022) or the native pipe |> come into play: Both operators pass (or “pipe”) the result of one operation (i.e., the output of a function) as an input to another operation (i.e., as the first argument of another function).

13.2 The pipe operator

The dplyr R package is awesome.
Pipes from the magrittr R package are awesome.
Put the two together and you have one of the most exciting things to happen to R in a long time.

Sean C. Anderson (2014)

The pipe operator from the magrittr package (Bache & Wickham, 2022) is a simple tool for data manipulation. Essentially, its so-called pipe operator %>% allows chaining commands in which the current result is passed to the next command (from left to right). With such forward pipes, a sequence of simple commands can be chained into a compound command.

The pipe operator will be particularly useful when transforming tables with dplyr (in Section 13.3) and tidyr (in Section 14.2 of Chapter 14). But before diving into the depths data transformation, we show that the pipe is an interesting tool in itself.

13.2.1 Using pipes

Figure 13.1: Ceci est un pipe: %>% (from magrittr). In base R, |> represents a pipe operator.

What is a pipe? While some people see pipes primarily as smoking devices, others may recall representational issues in art history (see Wikipedia: The treachery of images). But a better analogy for the use of pipes in R is more pragmatic and profane: In the applied sub-domain of physics known as plumbing, a pipe is a device for directing fluid and solid substances from one location to another.

In R, the pipe is an operator that allows re-writing a nested call to multiple functions as a chain of individual functions. Historically, the native forward pipe operator |> of base R (introduced in R version 4.1.0, published on 2021-05-18) was preceded by the %>% operator of the magrittr package (Bache & Wickham, 2022). Despite some differences, both pipes allow turning a nested expression of function calls into a linear sequence of simple processing steps. This sequence is easier to understand and avoids the need for saving intermediate results.

An indicator of the pipe’s popularity is the existence of a corresponding keyboard shortcut. When using the the RStudio IDE, typing the key combination Cmd + Shift + M inserts the %>% operator (or the |> operator, when selecting “Select native pipe operator” in the Code section of Global options).

In the following examples, we mostly use the %>% operator of magrittr, but most examples would be the same for the native pipe operator |>.

Basic usage

For our present purposes, it is sufficient to think of the pipe operator %>% as passing whatever is on its left (or left-hand-side, abbreviated as lhs) to the first argument of the function on its right (or right-hand-side, rhs):

# Native pipe (base R):
lhs |>  rhs

# Original pipe (magrittr):
lhs %>% rhs

Here, lhs is an expression (i.e., typically an R function) that yields some output object (e.g., a number, vector, or table), and rhs is an expression that uses this object as an input (i.e., an argument of an R function).

This description of an interaction between R expressions sounds more complicated than it is in practice. Actually, we are quite familiar with R expressions combine multiple steps. But so far, we have been nesting them in arithmetic formulas (with parentheses indicating operator precedence) or in hierarchical function calls, as in:

((x + 1) * 2)
prod(sum(x, 1), 2)

Using the pipe operator %>% of magrittr allows us to re-write the nested function calls into a linear chain of steps:

x %>% sum(1) %>% prod(2)

Thus, given three functions a(), b() and c(), the following pipe would compute the result of the compound expression c(b(a(x))):

# Apply a to x, then b, then c: 
x %>% a() %>% b() %>% c()

As the intermediate steps get longer and more complicated, we typically re-write the same pipe sequence as follows:

x %>% 
  a() %>% 
  b() %>% 
  c()

Assigning pipe results

Importantly, the pipe function of passing values differs from the assignment of a value to a name or variable, as achieved by R’s assignment operator <- (see Section 13.2.2 for details and examples). Thus, to assign the result of a pipe to some object y, we use the assignment operator <- at the (top) left of the pipe:

# Apply a to x, then b, then c 
# & assign the result to y: 
y <- x %>% a() %>% b() %>% c()

# typically written as:
y <- x   %>% 
     a() %>% 
     b() %>% 
     c()

# but the following also works:
x %>% a() %>% b() %>% c() -> y

13.2.2 Example pipes

When transforming data, we mostly use pipes for manipulating tables into other tables. However, the following examples illustrate that pipes can be used for other tasks as well.

Arithmetic pipes

Whereas a description of the pipe operator may sound complicated, the underlying idea is quite simple: We often want to perform several operations in a row or sequence. This is familiar to most of us when computing arithmetic expressions. For instance, consider the following step-by-step instruction:

• Start with a number x (e.g., 3). Then,
  
• multiply it by 4,
• add 20 to the result,
• subtract~7 from the result, and finally
• take the square root of the result.

When translating this sequence of steps into arithmetic notation, we could express its first step as \(x = 3\) and combine the next four steps into an expression \(\sqrt{x \cdot 4 + 20 - 7}\). Beyond knowing basic mathematical facts and operations, understanding this expression requires familiarity with arithmetic conventions and notations that determine the order of operations (e.g., reading from left to right, and rules like multiplying before adding or subtracting). To explicate the order of the elementary computations, we could use parentheses (e.g., \(\sqrt{((x \cdot 4) + 20) - 7}\)).

When translating an arithmetic expression into R code, similar conventions and rules govern the way we need to form our expression. In our example, we can first assign an object x to 3 (i.e., using assignment to create a numeric vector of length 1). The following arithmetic operations can then be invoked by using a mix of functions, arithmetic operators, and precedence rules:

x <- 3
sqrt(x * 4 + 20 - 7)
#> [1] 5

Here, we can immediately spot the sqrt() function, but the arithmetic operators *, + and - also implement arithmetic functions, and the order of their execution is determined by conventions (or explicated by parentheses). Avoiding the infix operators * and +, we can re-write the expression as a nested combination of R functions:

sqrt(sum(prod(x, 4), 20, -7))
#> [1] 5

When combining multiple functions, the order of their evaluation is determined by their level of encapsulation in parentheses. In R expressions, inner functions are evaluated before outer functions (e.g., prod() is evaluated first and sqrt() is evaluated last). As this order of evaluation conflicts with our habit of reading and writing from left to right, expressions containing multiple functions are difficult to parse and understand.

The R pipe operators |> or %>% allow us re-writing the sequence of functions as a chain:

# Arithmetic pipe (using base R):
x |> prod(4) |> sum(20) |> sum(-7) |> sqrt()
#> [1] 5

# OR (using magrittr):
x %>% prod(4) %>% sum(20) %>% sum(-7) %>% sqrt()
#> [1] 5

Note that the pipe notation corresponds closely to the step-by-step instructions above, particularly when we re-format the pipe to span multiple lines:

x |> 
  prod(4) |> 
  sum(20) |> 
  sum(-7) |> 
  sqrt()
#> [1] 5

Thus, the pipe operator aligns the notation of functional expressions more closely with the order of their evaluation. The pipe may only provide a new notation, but allows us express chains of R functions in a way that matches their natural language description. Overall, piped expressions are powerful by aligning how we think with what is being computed in R.

The dot notation (of magrittr)

If we find the lack of an explicit representation of each step’s result on the right hand side of %>% confusing, we can re-write the magrittr pipe as follows:

# Arithmetic pipe (using the dot notation of magrittr):
x %>% prod(., 4) %>% sum(., 20, -7) %>% sqrt(.)
#> [1] 5

Here, the dot . of the magrittr pipe operator is a placeholder for entering the result of the left (lhs) on the right (rhs). Thus, the . represents whatever was passed (or “piped”) from the left to the right (here: the current value of x).

The key benefit of using the dot placeholder notation is that we may occasionally want the result of the left expression to be passed to a non-first argument of the right expression. When using R for statistics, a typical example consists in passing data to a linear model:

# The linear model:
lm(Sepal.Length ~ Petal.Length, data = iris)

# can be re-written as a pipe (with dot notation):
iris %>% 
   lm(Sepal.Length ~ Petal.Length, data = .)

As both of these expressions effectively call the same lm() function, they also yield the same result:

#> 
#> Call:
#> lm(formula = Sepal.Length ~ Petal.Length, data = .)
#> 
#> Coefficients:
#>  (Intercept)  Petal.Length  
#>       4.3066        0.4089

By contrast, the base R pipe operator |> does not support the dot notation:

# ERROR: No dot notation in the base R pipe:
x |> prod(., 4) |> sum(., 20, -7) |> sqrt(.)
#> Error: object '.' not found

iris |>
   lm(Sepal.Length ~ Petal.Length, data = .)
#> Error in eval(mf, parent.frame()): object '.' not found

Another difference between both operators is that the magrittr pipe %>% allows dropping the parentheses when calling a function with no other arguments, whereas the native pipe |> always requires the parentheses. (See Differences between the base R and magrittr pipes (by Hadley Wickham, 2023-04-21) for additional details.)

The pipe vs. assignment

As mentioned above, we must not confuse the pipe with R’s assignment operator <-. Although %>% or |> may look and seem somewhat similar to the assignment operator <- (which also works as = or ->), they are and provide different functions. Importantly, the pipe does not assign new objects, but rather apply a function to an existing object that then may serve as an input of another function. The concrete input object changes every time a function is being applied and eventually results in an output object.

What happens if we tried to use a pipe to assign something to a new object \(y\)? Assuming there is no function y() defined in our current environment, the following code does not assign anything to y, but instead yields an error:

# The pipe does NOT assign objects:

# ERROR with base R pipe:
x |> y

# ERROR with magrittr pipe:
x %>% y
#> Error in y: The pipe operator requires a function call as RHS (<input>:4:6)

Thus, for actually assigning the result of a pipe to an object y, we need to use our standard assignment operator on the left (or at the beginning) of the pipe:

# Pipe and assignment by `<-`:
y <- x %>% 
  prod(4) %>% 
  sum(20, -7) %>% 
  sqrt()

y  # evaluates to:
#> [1] 5

The following also works, but using <- (above) is clearer than using ->:

# Pipe and alternative assignment by `->`:
x %>% 
  prod(4) %>% 
  sum(20, -7) %>% 
  sqrt() -> y

y  # evaluates to:
#> [1] 5

13.2.3 Evaluation

Overall, the effects of the pipe operators %>% and |> are similar to introducing a new mathematical notation: They do not allow us to do anything we could not do before, but allow us re-writing chains of commands in a more natural, sequential fashion. Essentially, embedded or nested calls of functions within functions are untangled into a linear chain of processing steps. This only re-writes R expressions, but in a way that corresponds more closely to how we think about them (i.e., making them easier to parse and understand).

Piped expressions are particularly useful when generating and transforming data objects (e.g., vectors or tables) by a series of functions that all share the same type of inputs and outputs (e.g., vectors or tables). As using the pipe avoids the need for saving intermediate objects, it makes complex sequences of function calls easier to construct, write, and understand.

While using pipes can add convenience and reduce complexity, these benefits also have some costs. From an applied perspective, a key requirement for using the pipe is that we must be aware of the data structures serving as inputs and outputs at each step. More importantly, piping functions implies that we do not need a record of all intermediate results. Whenever the results of intermediate steps are required later, we still have to assign them to corresponding objects. From a programming perspective, enabling piped expressions requires that R functions accept some key input as their first argument (unless we use the . notation of magrittr). Fortunately, most R functions are written in just this way, but it is something to keep in mind when writing our own functions.

13.2.4 Piping color palettes

When using R for data analysis and statistics, piped expressions are primarily used for transforming data tables into other data tables. However, the pipe operator %>% can be used in other contexts as well, provided functions are written in ways that enable their combination into pipes. As a concrete and colorful example, we will illustrate piped expressions in common visualization tasks. For instance, consider the usecol() and seecol() functions of the unikn package (Neth & Gradwohl, 2024):

library(unikn)

Besides defining some custom colors (like Seeblau or Pinky), the unikn package provides two main functions for creating and viewing color palettes:

• The usecol() function uses an input argument pal to define a color palette (e.g., as a vector of color names) and extends this palette to n values. Its output is a color palette (as a vector of color codes).

• The seecol() function shows and provides detail information on a given color palette.

A typical task when selecting colors is to define a new color palette and then visually inspecting them. As the first input argument of seecol() matches the output of usecol(), we can use the pipe operator to chain both commands:

usecol(c(Seeblau, "white", Pinky), n = 7) %>% 
  seecol(main = "My new color palette")

A more traditional (and explicit) version of the same commands would first use usecol() for defining a color palette as an R object (e.g., by assigning it to my_col) and then use this as the first argument of the seecol() function:

my_col <- usecol(c(Seeblau, "white", Pinky), n = 7) 
seecol(pal = my_col, main = "My new color palette")

Note that both of these code snippets call the same functions and thus create identical visualizations. However, using the pipe did not define the color palette my_col as a separate object in our environment. The piped chain solution is more compact and immediate, but only the second solution would allow us to re-use my_col later. Again, we see that the benefits and costs of piped expressions depend on what we want to do with the objects that are being created and manipulated.

13.2.5 Practice pipes

Native pipes

Assume the following objects:

v <- 1:3
x <- v[1]; y <- v[2]; z <- v[3]

and re-write the following magrittr pipes by only using the base R pipe |>:

x %>% c(y) %>% prod(z) 
v %>% rev %>% sum
x %>% c(y, .) %>% sum %>% all.equal(., z)
x %>% sum(y, .) %>% `^`(., z)

Solution

The following assume an R version 4.1.0 (published on 2021-05-18) or newer:

x |> c(y) |> prod(z) 
v |> rev() |> sum()
x |> c(y) |> sum() |> all.equal(z)
(x |> sum(y))^z

Note: As the native R pipe operator |> does not support the . (dot or placeholder) notation, the last expression transformed the function '^'(., z) into the arithmetic infix operator .^z.

Colorful pipes

The grepal() function of unikn searches all R color names (in colors()) for some term (e.g., “gold”, “orange”, or “white”) and returns the corresponding colors.

• Construct some color pipes that finds different versions of key colors and displays the corresponding colors.

• Are there more “black” or more “white” colors in R?

• How many shades of grey are provided by colors()?

Solution

A pipe that shows all “orange” colors (i.e., colors with “orange” in their name) would be:

grepal("orange") %>% 
  seecol(main = "Shades of 'orange' in R")

There is only one “black”, but many different types of “white” in R:

grepal("black") %>% seecol()
grepal("white") %>% seecol()

# Note: 
grepal("grey")  %>% seecol()
grepal("dark")  %>% seecol()
grepal("light") %>% seecol()

Overall, these examples have shown that pipe operators facilitate writing R expressions in arithmetic and visualization contexts. However, the primary use of pipes in R consists in transforming data.

Transforming data with pipes

As we have seen, R pipe operators are a tool for providing data inputs to functions. This functionality is particularly useful when modifying tables of data (i.e., data frames or tibbles) by R functions that are designed to re-shape or reduce data. In the rest of this and in the next chapter, we will be using pipes to illustrate the tools provided by two popular tidyverse packages:

• Section 13.3 of this chapter: Transforming tables with dplyr (Wickham, François, et al., 2023)

• Section 14.2 of Chapter 14: Transforming tables with tidyr (Wickham & Girlich, 2024)

A good question to occasionally ask ourselves is: If both these packages transform data tables, what is the difference between dplyr and tidyr? We will revisit this question after introducing the essential commands of both packages (in Section 14.3.1).

13.3 Transforming tables with dplyr

The dplyr package (Wickham, François, et al., 2023) is a core component of the tidyverse. Like ggplot2, dplyr is widely used by people who otherwise do not reside within the tidyverse. But as dplyr is a package that is both immensely useful and embodies many of the tidyverse principles in paradigmatic form, we can think of it as the primary citizen of the tidyverse.

dplyr provides a set of functions — best thought of as verbs — that allow slicing and dicing rectangular datasets and computing many summary statistics. While each individual function is simple, they can be combined (e.g., by pipes) into a powerful language of data manipulation. In combination with other functions, using dplyr provides us with quick overviews of datasets that amount to what psychologists often call descriptive statistics. Although a descriptive understanding of data is no substitute for statistical testing or scientific insight, it is an important pre-requisite of both.

The following sections merely provide a summary of essential dplyr functions. More extensive resources for this section include:

• Chapter 3: Transforming data of the ds4psy book (Neth, 2023a).

• Chapter 5: Data transformation of the r4ds book (Wickham & Grolemund, 2017).

• The documentation of the dplyr package (Wickham, François, et al., 2023).

13.3.1 The function of pliers

The name of the dplyr package is inspired by the notion of “pliers”:

Figure 13.2: Pliers are tools for pulling out things or twisting their shapes. (Image by Evan-Amos, via Wikimedia Commons.)

Pliers are tools for pulling out parts and tugging, tweaking, or twisting things into different shapes (see Figure 13.2). In our current context, the thing to tweak is a rectangular set of data (as an R data frame or tibble) and the dplyr tool allows manipulating this table into other tables that contain parts, additional or fewer variables, or provide summary information.

dplyr = MS Excel + control

For users that are familiar with basic spreadsheet in MS Excel: The dplyr functions allow similar manipulations of tabular data in R. However, spreadsheet users are typically solving many tasks by clicking interface buttons, entering simple formulas, and many copy-and-paste operations. While this can be simple and engaging, it is terribly error prone. The main problem with spreadsheets is that the process, typically consisting of many small interactive steps, remains transient and is lost, as only the resulting data table is stored. If a sequence of 100 steps included a minor error on step 29, we often need to start from scratch. Thus, it is very easy to make mistakes and almost impossible to recover from them if they are not noticed immediately.

By contrast, dplyr provides a series of functions for solving (sequences of) simple data manipulation tasks (e.g., arranging or selecting rows or columns, categorizing variables into groups, and computing simple summary tables). Rather than incrementally constructing a spreadsheet and many implicit cut-and-paste operations, dplyr uses sequences of simple functions that explicate the entire process. In the spirit of reproducible research (see Section 1.3), this documents precisely what is being done and allows making corrections later.

13.3.2 Essential dplyr functions

The following sections will briefly illustrate essential dplyr functions and their corresponding tasks:

1. arrange() sorts cases (rows);
2. filter() and slice() select cases (rows) by logical conditions;
3. select() selects and reorders variables (columns);
4. mutate() and transmute() compute new variables (columns) out of existing ones;
5. summarise() collapses multiple values of a variable (rows of a column) to a single one;
   
6. group_by() changes the unit of aggregation (in combination with mutate() and summarise()).

Learning dplyr essentially consists in learning and applying these functions as the verbs of a new language. And just as the words of a language are typically combined into longer sequences (e.g., sentences, paragraphs, etc.) dplyr functions are often combined into longer data transformation pipes. Studying a few examples of each function will make it easy and straightforward to combine them into powerful pipes that allow slicing, dicing, and summarizing large data tables.

Example data

Section 3.2: Essential dplyr commands uses the starwars data from the dplyr package:

sw <- dplyr::starwars
dim(sw)
#> [1] 87 14

The starwars data is a tibble containing 87 cases (rows) and 14 variables (columns). See ?dplyr::starwars for a description of the data and its variables.

To provide additional examples, we use the storms data from the dplyr package in this chapter:

st <- dplyr::storms
dim(st)
#> [1] 11859    13

The storms data is a tibble containing 11859 cases (rows) and 13 variables (columns). See ?dplyr::storms for a description of the data and its variables.

A key difference between the storms and the starwars data lies in their units of observations: Each row of starwars corresponds to an individual creature, so that each individual creature appears in exactly one row. By contrast, each row in storms describes a particular observation of a storm, but the same storm can be observed at multiple times (i.e., appears in multiple lines). As a consequence, working with the storms data is slightly more challenging than working with the starwars data.

The following examples use the storms data. If you find any of them difficult to understand, check out Section 3.2: Essential dplyr commands of the ds4psy book (Neth, 2023a), which provide corresponding examples based on the starwars data.

1. Using arrange() to sort cases (rows)

The arrange() function keeps all data, but arranges its cases (rows) by the variable (column) mentioned:

# Re-arrange data:
st %>%
  arrange(month)

#> # A tibble: 11,859 × 13
#>    name   year month   day  hour   lat  long status        categ…¹  wind press…²
#>    <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>         <ord>   <int>   <int>
#>  1 Zeta   2006     1     1     0  25.6 -38.3 tropical sto… 0          50     997
#>  2 Zeta   2006     1     1     6  25.4 -38.4 tropical sto… 0          50     997
#>  3 Zeta   2006     1     1    12  25.2 -38.5 tropical sto… 0          50     997
#>  4 Zeta   2006     1     1    18  25   -38.6 tropical sto… 0          55     994
#>  5 Zeta   2006     1     2     0  24.6 -38.9 tropical sto… 0          55     994
#>  6 Zeta   2006     1     2     6  24.3 -39.7 tropical sto… 0          50     997
#>  7 Zeta   2006     1     2    12  23.8 -40.4 tropical sto… 0          45    1000
#>  8 Zeta   2006     1     2    18  23.6 -40.8 tropical sto… 0          50     997
#>  9 Zeta   2006     1     3     0  23.4 -41   tropical sto… 0          55     994
#> 10 Zeta   2006     1     3     6  23.3 -41.3 tropical sto… 0          55     994
#> # … with 11,849 more rows, 2 more variables:
#> #   tropicalstorm_force_diameter <int>, hurricane_force_diameter <int>, and
#> #   abbreviated variable names ¹​category, ²​pressure

Arranging rows by multiple variables is also possible:

# Re-arrange data (by multiple variables):
st %>%
  arrange(lat, long)

#> # A tibble: 11,859 × 13
#>    name     year month   day  hour   lat  long status      categ…¹  wind press…²
#>    <chr>   <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>       <ord>   <int>   <int>
#>  1 Isidore  1990     9     4     0   7.2 -23.4 tropical d… -1         25    1010
#>  2 Isidore  1990     9     4     6   7.4 -25.1 tropical d… -1         25    1010
#>  3 Kirk     2018     9    22     6   7.7 -21.8 tropical d… -1         30    1007
#>  4 Kirk     2018     9    22    12   8.1 -22.9 tropical s… 0          35    1005
#>  5 Pablo    1995    10     4    18   8.3 -31.4 tropical d… -1         30    1009
#>  6 Pablo    1995    10     5     0   8.4 -32.8 tropical d… -1         30    1009
#>  7 Isidore  1990     9     4    12   8.4 -26.7 tropical d… -1         25    1009
#>  8 Kirk     2018     9    22    18   8.5 -24.1 tropical s… 0          35    1005
#>  9 Isidore  1996     9    24    12   8.6 -23.3 tropical d… -1         25    1008
#> 10 Arthur   1990     7    22     6   8.8 -41.9 tropical d… -1         25    1010
#> # … with 11,849 more rows, 2 more variables:
#> #   tropicalstorm_force_diameter <int>, hurricane_force_diameter <int>, and
#> #   abbreviated variable names ¹​category, ²​pressure

The arrange() function sorts text variables (of type “character”) in alphabetical and numeric variables (of type “integer” or “double”) in ascending order. Use desc() to sort a variable in the opposite order:

# Re-arrange data (in descending order):
st %>%
  arrange(desc(name), desc(lat))

#> # A tibble: 11,859 × 13
#>    name   year month   day  hour   lat  long status        categ…¹  wind press…²
#>    <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>         <ord>   <int>   <int>
#>  1 Zeta   2020    10    29    12  35.3 -83.6 tropical sto… 0          45     990
#>  2 Zeta   2020    10    29     6  32.8 -87.5 tropical sto… 0          60     986
#>  3 Zeta   2020    10    29     0  30.2 -89.9 hurricane     2          85     973
#>  4 Zeta   2020    10    28    21  29.2 -90.6 hurricane     3         100     970
#>  5 Zeta   2020    10    28    18  28   -91.1 hurricane     2          95     973
#>  6 Zeta   2020    10    28    12  26   -91.7 hurricane     1          80     978
#>  7 Zeta   2005    12    31     6  25.7 -37.6 tropical sto… 0          50     997
#>  8 Zeta   2005    12    31    12  25.7 -37.9 tropical sto… 0          50     997
#>  9 Zeta   2005    12    31    18  25.7 -38.1 tropical sto… 0          45    1000
#> 10 Zeta   2005    12    31     0  25.6 -37.3 tropical sto… 0          45    1000
#> # … with 11,849 more rows, 2 more variables:
#> #   tropicalstorm_force_diameter <int>, hurricane_force_diameter <int>, and
#> #   abbreviated variable names ¹​category, ²​pressure

Note that the variable names specified in arrange() — or in other dplyr functions — are not enclosed in quotation marks. This may seem a bit strange at first, but becomes totally intuitive after typing a few commands.

2. Using filter() or slice() to select cases (rows)

Many questions concern only a subset of the cases (rows) of our data. In these instances, a typical first step consists in filtering rows for particular values on one or more variables. For instance, the following command reduces the 11859 rows of the st data quite drastically by only including rows in which the wind speed exceeds 150 knots:

# Select cases (rows) based on a condition:
st %>% 
  filter(wind > 150)

#> # A tibble: 12 × 13
#>    name     year month   day  hour   lat  long status    category  wind pressure
#>    <chr>   <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>     <ord>    <int>    <int>
#>  1 Gilbert  1988     9    14     0  19.7 -83.8 hurricane 5          160      888
#>  2 Gilbert  1988     9    14     6  19.9 -85.3 hurricane 5          155      889
#>  3 Mitch    1998    10    26    18  16.9 -83.1 hurricane 5          155      905
#>  4 Mitch    1998    10    27     0  17.2 -83.8 hurricane 5          155      910
#>  5 Rita     2005     9    22     3  24.7 -87.3 hurricane 5          155      895
#>  6 Rita     2005     9    22     6  24.8 -87.6 hurricane 5          155      897
#>  7 Wilma    2005    10    19    12  17.3 -82.8 hurricane 5          160      882
#>  8 Dorian   2019     9     1    12  26.5 -76.5 hurricane 5          155      927
#>  9 Dorian   2019     9     1    16  26.5 -77   hurricane 5          160      910
#> 10 Dorian   2019     9     1    18  26.5 -77.1 hurricane 5          160      910
#> 11 Dorian   2019     9     2     0  26.6 -77.7 hurricane 5          155      914
#> 12 Dorian   2019     9     2     2  26.6 -77.8 hurricane 5          155      914
#> # … with 2 more variables: tropicalstorm_force_diameter <int>,
#> #   hurricane_force_diameter <int>

As before, filter() can use multiple variables and include numeric and character variables:

# Select cases (rows) based on several conditions:
st %>% 
  filter(year > 2014, month == 9, status == "hurricane")

#> # A tibble: 234 × 13
#>    name     year month   day  hour   lat  long status    category  wind pressure
#>    <chr>   <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>     <ord>    <int>    <int>
#>  1 Fred     2015     9     1     0  17.4 -24.9 hurricane 1           65      991
#>  2 Joaquin  2015     9    30     6  25.4 -71.8 hurricane 1           65      978
#>  3 Joaquin  2015     9    30    12  24.9 -72.2 hurricane 1           70      971
#>  4 Joaquin  2015     9    30    18  24.4 -72.5 hurricane 1           80      961
#>  5 Gaston   2016     9     1     0  35.5 -46.3 hurricane 2           90      969
#>  6 Gaston   2016     9     1     6  36.3 -44.3 hurricane 2           85      973
#>  7 Gaston   2016     9     1    12  37.1 -42   hurricane 1           80      976
#>  8 Gaston   2016     9     1    18  37.8 -39.5 hurricane 1           75      981
#>  9 Gaston   2016     9     2     0  38.2 -37   hurricane 1           70      985
#> 10 Gaston   2016     9     2     6  38.5 -35   hurricane 1           65      988
#> # … with 224 more rows, and 2 more variables:
#> #   tropicalstorm_force_diameter <int>, hurricane_force_diameter <int>

A variant of filter() is slice(), which is used to select particular rows, which are either described by some number or some combination of a property and a number:

# Select cases (rows): 
st %>% slice_head(n = 3)  # select the first 3 cases

#> # A tibble: 3 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 Amy    1975     6    27     0  27.5   -79 tropi… -1         25    1013      NA
#> 2 Amy    1975     6    27     6  28.5   -79 tropi… -1         25    1013      NA
#> 3 Amy    1975     6    27    12  29.5   -79 tropi… -1         25    1013      NA
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

st %>% slice_tail(n = 3)  # select the last 3 cases

#> # A tibble: 3 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 Iota   2020    11    18     0  13.8 -86.7 tropi… 0          40    1000     140
#> 2 Iota   2020    11    18     6  13.8 -87.8 tropi… 0          35    1005     140
#> 3 Iota   2020    11    18    12  13.7 -89   tropi… -1         25    1006       0
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

st %>% slice_max(pressure, n = 3)  # select cases with 3 maximal values 

#> # A tibble: 3 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 AL07…  2003     7    26    12  32.3 -82   tropi… -1         20    1022      NA
#> 2 AL07…  2003     7    26    18  32.8 -82.6 tropi… -1         15    1022      NA
#> 3 AL07…  2003     7    27     0  33   -83   tropi… -1         15    1022      NA
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

st %>% slice_min(pressure, n = 3)  # select cases with 3 minimial values

#> # A tibble: 3 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 Wilma  2005    10    19    12  17.3 -82.8 hurri… 5         160     882     265
#> 2 Gilb…  1988     9    14     0  19.7 -83.8 hurri… 5         160     888      NA
#> 3 Gilb…  1988     9    14     6  19.9 -85.3 hurri… 5         155     889      NA
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

st %>% slice_sample(n = 3)  # select 3 random cases

#> # A tibble: 3 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 Jose…  2008     9     3    18  13.8 -29.2 tropi… 0          55     994     180
#> 2 Bonn…  1992     9    20    12  36.5 -56   hurri… 2          85     974      NA
#> 3 Nico…  2016    10    12     0  27.4 -66.6 hurri… 1          75     976     180
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

Note that filter() and slice() reduced the number of cases (rows), but left the number of variables (columns) intact. The complement is select(), which has the opposite effects.

3. Using select() to select variables (columns)

The select() function provides an easy way of selecting and re-arranging the variables (columns) of tables:

# Select some variables (columns): 
st %>%
  select(name, pressure, wind)

#> # A tibble: 11,859 × 3
#>    name  pressure  wind
#>    <chr>    <int> <int>
#>  1 Amy       1013    25
#>  2 Amy       1013    25
#>  3 Amy       1013    25
#>  4 Amy       1013    25
#>  5 Amy       1012    25
#>  6 Amy       1012    25
#>  7 Amy       1011    25
#>  8 Amy       1006    30
#>  9 Amy       1004    35
#> 10 Amy       1002    40
#> # … with 11,849 more rows

Important assets of select() are its additional features:

• va:vx selects a range of variables (e.g., from va to vx);
• !vy allows negative selections (e.g., selecting all variables except vy);
• & or | selects the intersection or union of two sets of variables;
• starts_with("abc") and ends_with("xyz") selects all variables whose names start or end with some characters (e.g., “abc” or “xyz”);
• everything() selects all variables not selected yet (e.g., to re-order all variables).

Here are some typical examples for corresponding selections (adding slice_sample(n = 3) for showing only three random rows of the resulting table):

# Select a range of variables: 
st %>% select(name, year:day, lat:long) %>% slice_sample(n = 3)  

#> # A tibble: 3 × 6
#>   name    year month   day   lat  long
#>   <chr>  <dbl> <dbl> <int> <dbl> <dbl>
#> 1 Harvey  2005     8     6  33.5 -56.7
#> 2 Debby   1982     9    14  22.4 -71.8
#> 3 Lisa    2010     9    25  22.3 -28.3

# Select an intersection of negated variables:
st %>% select(!status & !ends_with("diameter")) %>% slice_sample(n = 3)  

#> # A tibble: 3 × 10
#>   name     year month   day  hour   lat  long category  wind pressure
#>   <chr>   <dbl> <dbl> <int> <dbl> <dbl> <dbl> <ord>    <int>    <int>
#> 1 Marilyn  1995     9    20     0  34.2 -66.8 1           80      974
#> 2 Harvey   1981     9    15     0  28.4 -62.6 4          115      946
#> 3 Hermine  1980     9    25     0  17.7 -95.5 0           45     1000

# Re-order the columns of a table (selecting everything):
st %>% select(year, name, lat:long, everything()) %>% slice_sample(n = 3)  

#> # A tibble: 3 × 13
#>    year name    lat  long month   day  hour status categ…¹  wind press…² tropi…³
#>   <dbl> <chr> <dbl> <dbl> <dbl> <int> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1  1996 Lili   33.2 -53.8    10    23     6 hurri… 1          65     985      NA
#> 2  2012 Sandy  29.7 -75.6    10    27    18 hurri… 1          70     960     690
#> 3  2018 Lesl…  34.2 -57.6    10     5     0 tropi… 0          55     984     410
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

When using a pipe for quickly answering some descriptive question, it is common practice to first apply some combination of filter() and slice() (for removing non-needed rows), and select() (for removing non-needed columns).

4. Using mutate() for computing new variables

A frequent task in data analysis consists in computing some new variable out of existing ones. Metaphorically, this can be viewed as “mutating” some table’s current information into slightly different form. The mutate() function of dplyr first names a new variable (e.g., var_new =) and then uses existing R expressions (e.g., arithmetic operators, functions, etc.) for computing the values of the new variable.

As an example, let’s combine some variables into a new date variable:

# Compute and add a new variable: 
st %>% 
  select(name, year, month, day) %>%  # select/remove variables
  mutate(date = paste(year, month, day, sep = "-")) %>%
  slice_sample(n = 5)  # show 5 random cases (rows)

#> # A tibble: 5 × 5
#>   name       year month   day date      
#>   <chr>     <dbl> <dbl> <int> <chr>     
#> 1 Danielle   1998     8    30 1998-8-30 
#> 2 Alex       1998     7    28 1998-7-28 
#> 3 Klaus      1984    11    11 1984-11-11
#> 4 Gabrielle  2019     9     8 2019-9-8  
#> 5 Hugo       1989     9    17 1989-9-17

In this example, we used the R function paste() to combine the three variables year, month, and day, into a single character variable. Note that the assignment to a new variable was signaled by the operator =, rather than R’s typical assignment operator <-. To make our example clear, we used the select() function to remove all variables not needed for this illustration. In most real-world settings, we would not remove all other variables, but rather add new variables to the existing ones (and occasionally use select() to re-order them). Note also that, when actually working with dates and times later, we would not transform date values into text objects. Instead, we use R functions for parsing date and time variables into dedicated variables that represent dates or date-times (see Chapter 10: Dates and times).

As with the other dplyr verbs, we can compute several new variables in one mutate() command by separating them by commas. If we wanted to get rid of the old variables, we could immediately remove them from the data by using transmute():

# Compute several new variables (replacing the old ones): 
st %>% 
  transmute(name = paste0(name, " (", status, ")"), 
            date = paste(year, month, day, sep = "-"),
            loc = paste0("(", lat, "; ", long, ")")) %>%
  slice_sample(n = 5)  # show 5 random cases (rows)

#> # A tibble: 5 × 3
#>   name                       date       loc          
#>   <chr>                      <chr>      <chr>        
#> 1 Jeanne (tropical storm)    2004-9-15  (17.1; -64)  
#> 2 Nine (tropical depression) 2015-9-17  (15.6; -45)  
#> 3 Humberto (hurricane)       2007-9-13  (29.5; -94.4)
#> 4 Marco (tropical storm)     1996-11-24 (16; -78)    
#> 5 Ana (tropical depression)  1979-6-23  (14; -61.3)

However, it is usually a bad idea to throw away source data. Especially since any act of computing new variables can be error-prone, we generally do not recommend using transmute(). Instead, a careful data analyst prefers mutate() for creating new variables and immediately checks whether the newly created variables are correct. And keeping all original variables is rarely a problem, as we always can remove unwanted variables (by selecting only the ones needed) later.

As both our examples so far have used mutate() or transmute() to create new character variables, here’s an example on numerical data. If we wanted to add a variable that rounds the values of pressure to the nearest multiple of 10, we could first divide these values by 10, round the result to the nearest integer (using the R function round(x, 0)), before multiplying by 10 again:

# Compute and add a new numeric variable: 
st %>% 
  mutate(press_10 = round(pressure/10, 0) * 10) %>%
  select(name, pressure, press_10) %>% 
  slice_sample(n = 5)  # show 5 random cases (rows)

#> # A tibble: 5 × 3
#>   name      pressure press_10
#>   <chr>        <int>    <dbl>
#> 1 Mitch          923      920
#> 2 AL042000      1011     1010
#> 3 Gabrielle      993      990
#> 4 Floyd          967      970
#> 5 Debby          995     1000

The immense power of mutate() lies in its use of functions for computing new variables out of the existing ones. As any R function can be used, the possibilities for creating new variables are limitless. However, note that the computations of each mutate() command are typically constrained to each individual case (row). This changes with the following two dplyr commands.

5. Using summarise() for aggregating over values of variables

Whereas mutate() computes new variables out of exiting ones for each case (i.e., by row), summarise() (and summarize()) computes summaries for individual variables (i.e., by column). Each summary is assigned to a new variable, using the same var_new = ... syntax as mutate(). The type of summary is indicated by applying a function to one or more variables. Useful functions for potential summaries include:

• Count: n(), n_distinct()

• Logical: any(), all()

• Center: mean(), median()

• Spread: sd(), IQR(), mad()

• Range: min(), max(), quantile()

• Position: first(), last(), nth()

When using summary functions, it is important to choose sensible names for the variables to which their results are being assigned. Here is a bad and a better example for naming summary variables:

# bad names:
st %>%
  summarise(n     = n(),
            name  = n_distinct(name),
            mean  = mean(wind),
            max   = max(wind))

#> # A tibble: 1 × 4
#>       n  name  mean   max
#>   <int> <int> <dbl> <int>
#> 1 11859   214  53.6   160

# better names:
st %>%
  summarise(nr        = n(),
            nr_names  = n_distinct(name),
            mean_wind = mean(wind),
            max_wind  = max(wind))

#> # A tibble: 1 × 4
#>      nr nr_names mean_wind max_wind
#>   <int>    <int>     <dbl>    <int>
#> 1 11859      214      53.6      160

Fortunately, if we fail to provide variable names, dplyr provides sensible default names:

# when not providing names:
st %>%
  summarise(n(),
            n_distinct(name),
            mean(wind),
            max(wind))

#> # A tibble: 1 × 4
#>   `n()` `n_distinct(name)` `mean(wind)` `max(wind)`
#>   <int>              <int>        <dbl>       <int>
#> 1 11859                214         53.6         160

Notice that using summarise() on a data table yields a modified — and typically much smaller — data table (as a tibble). Thus, summarise() is a function primarily used for reducing data.

Interestingly, we can immediately use a computed variable (like mean_wind or sd_wind) in a subsequent computation:

st %>%
  summarise(nr            = n(), 
            mean_wind     = mean(wind),
            sd_wind       = sd(wind),
            mean_minus_sd = mean_wind - sd_wind,
            mean_plus_sd  = mean_wind + sd_wind)
#> # A tibble: 1 × 5
#>      nr mean_wind sd_wind mean_minus_sd mean_plus_sd
#>   <int>     <dbl>   <dbl>         <dbl>        <dbl>
#> 1 11859      53.6    26.2          27.4         79.8

Summaries of columns are certainly nice to have, but nothing for which we needed a new function for. Instead, we could have simply computed the same summaries directly for the vectors of the st data:

nrow(st)
#> [1] 11859
n_distinct(st$name)
#> [1] 214
mean(st$wind)
#> [1] 53.63774
max(st$wind)
#> [1] 160

Thus, the true value of the summarise() function lies in the fact that it aggregates not only over all values of a variable (i.e., entire columns), but also over the levels of grouped variables, or all combinations of grouped variables. To use this feature, we need to precede a summarise() function by a group_by() function.

6. Using group_by() for changing the unit of aggregation

The group_by() function does very little by itself, but becomes immensely powerful in combination with other dplyr commands. To see how this works, let’s select only four variables from our st data and examine the effects of group_by():

st %>% 
  select(name, year, wind, pressure) %>%
  group_by(name)

#> # A tibble: 11,859 × 4
#> # Groups:   name [214]
#>    name   year  wind pressure
#>    <chr> <dbl> <int>    <int>
#>  1 Amy    1975    25     1013
#>  2 Amy    1975    25     1013
#>  3 Amy    1975    25     1013
#>  4 Amy    1975    25     1013
#>  5 Amy    1975    25     1012
#>  6 Amy    1975    25     1012
#>  7 Amy    1975    25     1011
#>  8 Amy    1975    30     1006
#>  9 Amy    1975    35     1004
#> 10 Amy    1975    40     1002
#> # … with 11,849 more rows

The resulting tibble contains all 11859 cases (rows) of st and the four selected variables. So what did the group_by(name) command do? Inspecting the output more closely shows the message: “Groups: name [198]”. This suggests that something has changed, even though we do not see any effects. Interestingly, the number of groups mentioned (i.e., 214) matches the number of distinct storm names that we obtained above by evaluating n_distinct(st$name). Let’s try a second command:

st %>% 
  select(name, year, wind, pressure) %>%
  group_by(name, year)

#> # A tibble: 11,859 × 4
#> # Groups:   name, year [512]
#>    name   year  wind pressure
#>    <chr> <dbl> <int>    <int>
#>  1 Amy    1975    25     1013
#>  2 Amy    1975    25     1013
#>  3 Amy    1975    25     1013
#>  4 Amy    1975    25     1013
#>  5 Amy    1975    25     1012
#>  6 Amy    1975    25     1012
#>  7 Amy    1975    25     1011
#>  8 Amy    1975    30     1006
#>  9 Amy    1975    35     1004
#> 10 Amy    1975    40     1002
#> # … with 11,849 more rows

The resulting tibble seems unaltered, but the message below the tibble dimensions now reads: “Groups: name, year [426]”. As there are 198 different values of name and the range of year values varies from 1975 to 2020, the number of 426 groups is not immediately obvious. As we will see momentarily, it results from the fact that some, but not all instances of name occur in more than one year.

The easiest way to identify the specific groups in both cases is to follow the last two statements by the count() function. This returns the groups (as the rows of a tibble) together with a variable n that counts the number of observations in each group:

# Group st by name and count (n of) observations per group:
st %>% 
  select(name, year, wind, pressure) %>%
  group_by(name) %>%
  count() %>%
  filter(name == "Felix") # show only one group

#> # A tibble: 1 × 2
#> # Groups:   name [1]
#>   name      n
#>   <chr> <int>
#> 1 Felix   178

# Group st by name, year and count (n of) observations per group:
st %>% 
  select(name, year, wind, pressure) %>%
  group_by(name, year) %>%
  count() %>%
  filter(name == "Felix") # show only one group

#> # A tibble: 4 × 3
#> # Groups:   name, year [4]
#>   name   year     n
#>   <chr> <dbl> <int>
#> 1 Felix  1989    57
#> 2 Felix  1995    59
#> 3 Felix  2001    40
#> 4 Felix  2007    22

Rather than returning the entire tibble, we added filter(name == "Felix") at the end to only return lines with this particular name value. When group_by(name), there is only one such group (containing 178 observations). By contrast, when group_by(name, year), there are four such groups (with a sum of 178 observations). Thus, a storm with the name Felix was observed in four distinct years.

ungroup() removes group()

The ungroup() function removes existing grouping factors. This is occasionally necessary for applying additional dplyr commands. For instance, if we first wanted to group storms by name and later draw a random sample of size n = 10 , we would need to add an intermediate ungroup() before applying slice_sample(n = 10) to the tibble of groups:

st %>%
  group_by(name) %>%
  ungroup() %>%
  slice_sample(n = 5)

#> # A tibble: 5 × 13
#>   name   year month   day  hour   lat  long status categ…¹  wind press…² tropi…³
#>   <chr> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <chr>  <ord>   <int>   <int>   <int>
#> 1 Jean…  1980    11    12     0  24.1 -87.4 hurri… 2          85     988      NA
#> 2 Erin   2007     8    16    12  28.1 -97.1 tropi… -1         30    1006       0
#> 3 Patty  2012    10    13     0  25.4 -71.9 tropi… 0          35    1007      30
#> 4 Evel…  1977    10    14     6  30.9 -64.9 tropi… 0          35    1005      NA
#> 5 AL02…  2003     6    11    12   9.7 -44.2 tropi… -1         30    1008      NA
#> # … with 1 more variable: hurricane_force_diameter <int>, and abbreviated
#> #   variable names ¹​category, ²​pressure, ³​tropicalstorm_force_diameter

Why do we want to group() data tables? The benefits of grouping become obvious by combining a group_by() function with a subsequent mutate() or summarise() function. In both cases, the unit of aggregation is changed from all cases to those within each group. The following sections provide examples for both combinations.

Grouped mutates

To illustrate the effects of a sequence of group_by() and mutate(), let’s compute the mean wind speed twice:

• the 1st use of mutate() computes the mean wind speed mn_wind_1 over all cases. The number of cases over which the mean is aggregated can be counted by the n() function (assigned to a variable mn_n_1).

• the 2nd use of mutate() also computes the mean wind speed mn_wind_2 and uses the same n() function (assigned to a variable mn_n_2). The key difference is not in the content of the mutate() function, but the fact that the 2nd mutate() is located after the group_by(name) expression. This changed the unit of aggregation to this particular group.

st %>%
  select(name, year, wind) %>%    # select some variables
  mutate(mn_wind_1 = mean(wind),  # compute mean 1
         mn_n_1 = n()) %>%        # compute nr 1
  group_by(name) %>%              #   group by name
  mutate(mn_wind_2 = mean(wind),  #   compute mean 2
         mn_n_2 = n()) %>%        #   compute n 2
  ungroup() %>%                   # ungroup
  slice_sample(n = 10)

#> # A tibble: 10 × 7
#>    name      year  wind mn_wind_1 mn_n_1 mn_wind_2 mn_n_2
#>    <chr>    <dbl> <int>     <dbl>  <int>     <dbl>  <int>
#>  1 Luis      1995   110      53.6  11859      96.7     52
#>  2 Georges   1998    90      53.6  11859      67.3     92
#>  3 Bonnie    1986    30      53.6  11859      52.4    209
#>  4 Ivan      2004    45      53.6  11859      79.3    141
#>  5 Frederic  1979   115      53.6  11859      52.6     66
#>  6 Lisa      2010    50      53.6  11859      45.0    122
#>  7 Michael   2012    50      53.6  11859      69.8     66
#>  8 Humberto  2001    25      53.6  11859      64.2    132
#>  9 Emily     2005   120      53.6  11859      59.6    217
#> 10 Arthur    2002    50      53.6  11859      39.0    119

To better inspect the resulting tibble, we followed the 2nd mutate() function with ungroup(). This removes any existing grouping operations and allows manipulating the table with the new variables. In this case, we used slice_sample(n = 10) to draw 10 random rows (out of the 11859 rows from st). These 10 rows show the difference in results of both mutate() commands. The first variable mn_wind_1 shows an identical value for all rows (as it computed the means over all 11859 rows). The second variable mn_wind_2 shows a different value for each name, as it was computed over those rows that shared the same name.

Beware that the results of grouped mutate() commands are easily misinterpreted: For instance, the values of mn_wind_2 could be misinterpreted as the mean wind speed of a particular storm. However, mn_wind_2 was only computed over those observations that shared the same name value. As some names occur repeatedly (in different years), the values do not necessarily refer to the same storm. Aggregating by storm would require a unique identifier for each storm (e.g., some combination of its name and date).

Grouped summaries

Perhaps even more frequent than following a group() function by mutate() is following it by summarise(). In this case, we aggregate the specified summaries over each group, rather than all data values.

To illustrate the effects of grouped summaries, compare the following three pipes of dplyr commands: All three contain the same summarise() part, which computes three new variables that report the number of cases in each summary n_cases, the mean wind speed mn_wind, and the maximum wind speed max_wind. The difference between the three versions lies in the group_by() statements prior to the summarise() command:

• the 1st pipe computes the summary for all of st (without grouping):

# Pipe 1:
st %>%
  summarise(n_cases = n(),
            mn_wind = mean(wind), 
            max_wind = max(wind))

#> # A tibble: 1 × 3
#>   n_cases mn_wind max_wind
#>     <int>   <dbl>    <int>
#> 1   11859    53.6      160

• the 2nd pipe computes the summary for each year of st:

# Pipe 2:
st %>%
  group_by(year) %>%
  summarise(n_cases = n(),
            mn_wind = mean(wind), 
            max_wind = max(wind))

#> # A tibble: 46 × 4
#>    year n_cases mn_wind max_wind
#>   <dbl>   <int>   <dbl>    <int>
#> 1  1975      86    50.9      100
#> 2  1976      52    59.9      105
#> 3  1977      53    54.0      150
#> 4  1978      54    40.5       80
#> 5  1979     301    48.7      150
#> 6  1980     161    53.7       90
#> # ℹ 40 more rows

• the 3rd pipe computes the summary for each year and month of st:

# Pipe 3:
st %>%
  group_by(year, month) %>%
  summarise(n_cases = n(),
            mn_wind = mean(wind), 
            max_wind = max(wind))

#> # A tibble: 227 × 5
#> # Groups:   year [46]
#>    year month n_cases mn_wind max_wind
#>   <dbl> <dbl>   <int>   <dbl>    <int>
#> 1  1975     6      16    37.5       60
#> 2  1975     7      14    56.8       60
#> 3  1975     8      40    45        100
#> 4  1975     9      16    73.8       95
#> 5  1976     8      18    68.1      105
#> 6  1976     9      18    56.4       90
#> # ℹ 221 more rows

Note that each pipe results in a tibble, but their dimensions differ considerably.
Whereas the first pipe yielded a compact 1 by 3 data structure, the 2nd one contained 48 rows and 4 columns, and the 3rd one contained 259 rows and 5 columns.

As we can use all kinds of R functions in the mutate() and summarise() parts, preceding them by group_by() allows computing all kinds of new variables and descriptive summary statistics. In the following, we illustrate how we can answer quite interesting questions by appropriate dplyr pipes.

13.3.3 Answering questions by data transformation

Using dplyr pipes to reshape or reduce tables and then either inspecting the resulting tibble or visualizing it with ggplot2 provides powerful combinations for data exploration. As we will address the topic of Exploring data more explicitly in Chapter 15, this section only provides some more advanced examples.

To illustrate the typical workflow, we will continue to work with the dplyr storms data (copied to st). So let’s ask some non-trivial questions and then provide a descriptive answer to it by summary tables and visualizations (i.e., a combination of dplyr and ggplot2 expressions).

Question

• What were the 10 storms with the highest wind speeds?

Answer

We can translate this question into the following one: What was the maximal wind speed that was recorded for each (named) storm?

st <- dplyr::storms  # copy data

st_top10_wind <- st %>%
  group_by(name) %>%
  summarise(max_wind = max(wind)) %>%
  arrange(desc(max_wind)) %>%
  slice(1:10)

st_top10_wind

#> # A tibble: 10 × 2
#>    name    max_wind
#>    <chr>      <int>
#>  1 Dorian       160
#>  2 Gilbert      160
#>  3 Wilma        160
#>  4 Mitch        155
#>  5 Rita         155
#>  6 Andrew       150
#>  7 Anita        150
#>  8 David        150
#>  9 Dean         150
#> 10 Felix        150

Question

• What was the maximal wind speed of each storm?

Answer

We arrange the rows by (descending) wind speed, then group it by the name of storms, and select only the top row of each group:

st_max_wind <- st %>% 
  arrange(desc(wind)) %>%
  group_by(name) %>%
  slice_head(n = 1) 

dim(st_max_wind)

#> [1] 214  13

The resulting table st_max_wind contains only 214 rows. Does this correspond to the number of unique storm names in st? Let’s check:

length(unique(st$name))
#> [1] 214

Note a key difference between the two tables st_top10_wind and st_max_wind: st_top10_wind is only a small summary table that answers our question from above, whereas st_max_wind is a much larger subset of the original data (and includes the same variables as st).

In fact, our summary information of st_top10_wind should be contained within st_max_wind. Let’s check this: Inspecting wind_top10 shows four storms with wind speeds of at least 150 knots. Do we obtain the same storms when filtering the table st_max_wind for these values? The following expressions verify this by re-computing the top-10 storm names from the data in st_max_wind:

top10_2 <- st_max_wind %>%
  filter(wind >= 150) %>%
  select(name, wind) %>%
  arrange(desc(wind))
top10_2

#> # A tibble: 12 × 2
#> # Groups:   name [12]
#>    name     wind
#>    <chr>   <int>
#>  1 Dorian    160
#>  2 Gilbert   160
#>  3 Wilma     160
#>  4 Mitch     155
#>  5 Rita      155
#>  6 Andrew    150
#>  7 Anita     150
#>  8 David     150
#>  9 Dean      150
#> 10 Felix     150
#> 11 Katrina   150
#> 12 Maria     150

all.equal(st_top10_wind$name, top10_2$name)

#> [1] "Lengths (10, 12) differ (string compare on first 10)"

Question

• What was the average wind speed (in knots) and pressure (in millibar) by storm category?

Answer

Using a dplyr pipe to compute a grouped summary table t_w:

t_w <- st %>% 
  group_by(category) %>%
  summarise(n = n(),
            mn_wind = mean(wind))

knitr::kable(t_w, caption = "Mean wind speed of storms (from **dplyr**).")

Table 13.1: Mean wind speed of storms (from dplyr).

category	n	mn_wind
-1	2898	27.49482
0	5347	45.66392
1	1934	70.95140
2	749	89.41923
3	434	104.48157
4	411	122.10462
5	86	145.58140

Using t_w to plot results with ggplot2:

ggplot(t_w, aes(x = category, y = mn_wind)) +
  geom_point(aes(size = n), col = "firebrick") +
  labs(tag = "A", title = "Wind speed by storm category", 
       x = "Storm category", y = "Wind speed (mean)") + 
  ylim(0, 150) + 
  theme_ds4psy()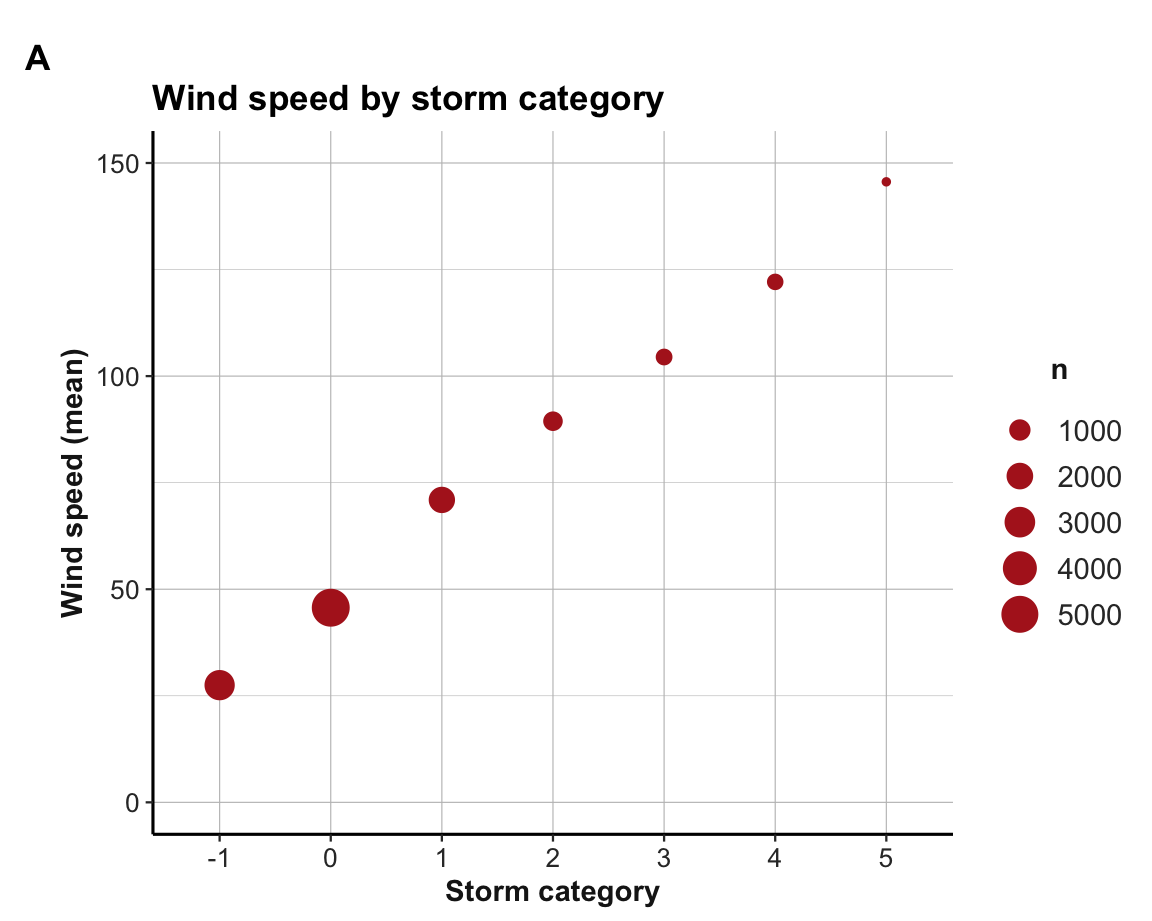

Note that the aesthetic mapping size = n expresses the frequency count as point size (i.e., visualizes a 2nd variable).

13.3.4 Practice: Using dplyr (and ggplot2)

The following exercises can be solved by pipes of dplyr and ggplot2 functions.

Exercise 1: Counting groups and visualizing two variables

Try answering the following questions by creating a dplyr pipe and a visualization that shows the solution:

• What was the average air pressure (in millibar) by storm category?
• How frequent is the corresponding storm category?

Solution

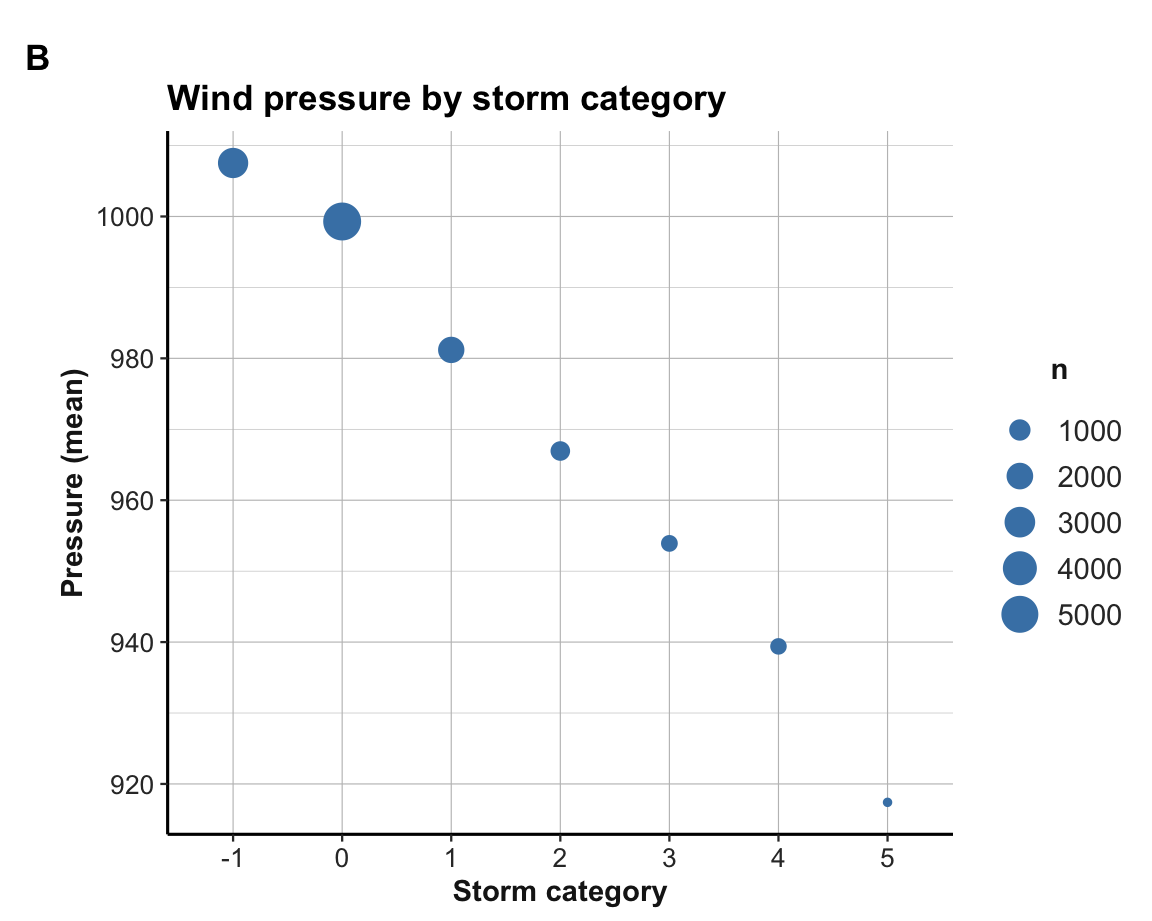
Using a dplyr pipe to compute a summary table t_p:

Table 13.2: Mean air pressure of storms (from dplyr).

category	n	mn_press
-1	2898	1007.5390
0	5347	999.2910
1	1934	981.1887
2	749	966.9359
3	434	953.9124
4	411	939.3942
5	86	917.4070

Using t_p to plot results with ggplot2:

Exercise 2: Plotting storm counts per category and month

Use the data from dplyr::storms to show that there are specific storm seasons throughout the year.

• How many storms of each category were recorded in each month?
• Is there an observable trend of storm observations over the calendar year?

1. To begin addressing these tasks, we could use a dplyr pipe to compute a grouped summary table that shows the number of storms per category and month:

#> # A tibble: 37 × 3
#> # Groups:   month [10]
#>    month category     n
#>    <dbl>    <dbl> <int>
#>  1     1        1     5
#>  2     1       NA    65
#>  3     4       NA    66
#>  4     5       NA   201
#>  5     6        1    18
#>  6     6       NA   791
#>  7     7        1   148
#>  8     7        2    35
#>  9     7        3    19
#> 10     7        4    18
#> # ℹ 27 more rows

2. Try using t_2 to plot results with ggplot2:

The following plot aims to visualize our summary table t_2:

ggplot(t_2, aes(x = factor(month))) +
  geom_bar(aes(fill = factor(category))) +
  labs(title = "Storm counts by category per month", 
       x = "Month", y = "Number of observations") + 
  theme_ds4psy()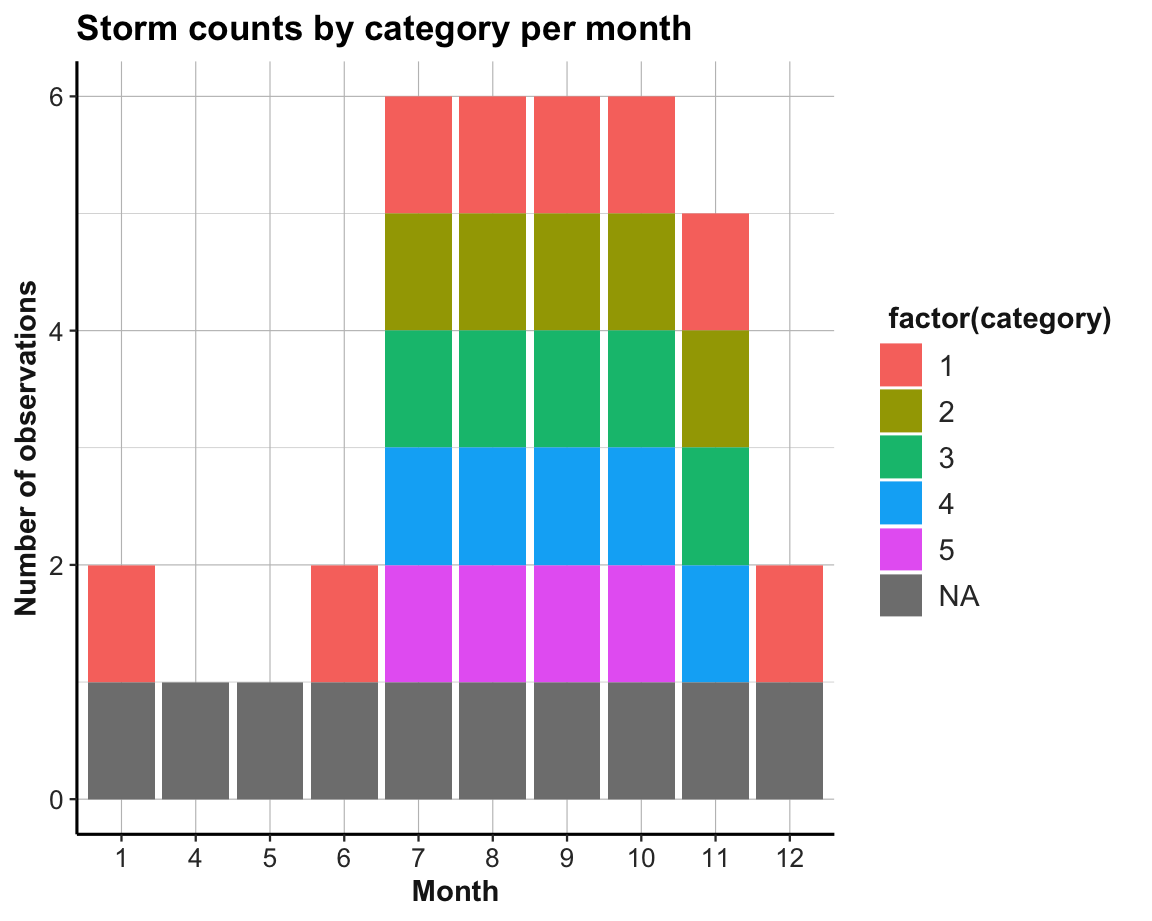

Figure 13.3: A misleading visualization: All storm category counts appear to be 0 or 1.

However, this plot seems wrong and is actually quite misleading.

• What’s the problem with it? How can it be fixed?

Solution

The problem is that the bar plot counted how often each category-month combination occurs in t_2 (with geom_bar() using its default stat = "count"). Thus, the only two possible counts for each combination of storm category and month are 0 (i.e., absence of a cell value) and 1 (i.e., presence of a cell value).

Here are two possible corrections of the misleading visualization:

1. Use the t_2 data, but geom_bar() using y = n and stat = "identity":

ggplot(t_2, aes(x = factor(month))) +
  geom_bar(aes(y = n, fill = category), stat = "identity") +
  labs(title = "Storm counts by category per month", 
       x = "Month", y = "Number of observations") + 
  theme_ds4psy()

2. Use the raw data of st and geom_bar() with default settings (i.e., stat = "count"):

ggplot(st, aes(x = factor(month))) +
  geom_bar(aes(fill = category, group = category)) +
  labs(title = "Storm counts by category per month", 
       x = "Month", y = "Number of observations") + 
  theme_ds4psy()

3. An alternative way to address this task may be to compute a better summary table (showing the counts of storms by category and month). The following solution uses tidyr functions (discussed in Chapter 14) to first re-shape the summary table t_2 from its long to a wider format:

Table 13.3: Number of storm observations per category and month.

month	NA	1	2	3	4	5
1	65	5	0	0	0	0
4	66	0	0	0	0	0
5	201	0	0	0	0	0
6	791	18	0	0	0	0
7	1430	148	35	19	18	1
8	3404	581	198	113	114	32
9	5314	1145	581	359	309	70
10	2335	466	150	86	88	13
11	949	152	29	16	24	0
12	179	33	0	0	0	0

Interpretation

• Both visualizations and the summary table suggest the same trend over the calendar year: The number of storms in all categories (including NA) increase in spring, peak in late summer (September), and rapidly decrease afterwards.

• Curiously, there are zero observations in the data in months 2 and 3 (i.e., February and March).

• A crucial limitation of all these solutions is that we were counting observations (i.e., rows) in our data, rather than storms. As some storms occur more often than others, the number of observations does not correspond to the number of storms per category.

Exercise 3: Names of re-occuring storms

1. Identify all storms in st that were observed in more than one year.

2. There are two ways in which a storm name can appear in more than one year:

• A single storm may occur in multiple years (e.g., from December to January)
• A storm name is used repeatedly (i.e., to name different storms in different years)

Check how often each of these cases occurs.

Solution

ad 1.: Grouping by the name and year variables, we first count the number of times a storm occurs per year. We then group by name to count storms occurring in more than one year.

st %>% 
  select(name, year) %>%
  group_by(name, year) %>%
  count() %>%
  # select(name, year) %>%
  group_by(name) %>%
  count() %>%
  filter(n > 1) %>%
  head() 

#> # A tibble: 6 × 2
#> # Groups:   name [6]
#>   name        n
#>   <chr>   <int>
#> 1 Alberto     7
#> 2 Alex        4
#> 3 Allison     3
#> 4 Ana         7
#> 5 Andrew      2
#> 6 Arthur      7

  # tail()

Verify these results for some storms:

• Does “Alberto” really occur in 6 different years?

st %>% 
  filter(name == "Alberto") %>%
  group_by(name, year) %>%
  count()
#> # A tibble: 7 × 3
#> # Groups:   name, year [7]
#>   name     year     n
#>   <chr>   <dbl> <int>
#> 1 Alberto  1982    17
#> 2 Alberto  1988    11
#> 3 Alberto  1994    32
#> 4 Alberto  2000    79
#> 5 Alberto  2006    18
#> 6 Alberto  2012    13
#> # … with 1 more row
#> # ℹ Use `print(n = ...)` to see more rows

• Does “Ana” really occur in 7 different years?

st %>% 
  filter(name == "Ana") %>%
  group_by(name, year) %>%
  count()
#> # A tibble: 7 × 3
#> # Groups:   name, year [7]
#>   name   year     n
#>   <chr> <dbl> <int>
#> 1 Ana    1979    19
#> 2 Ana    1985    14
#> 3 Ana    1991    12
#> 4 Ana    1997    15
#> 5 Ana    2003    13
#> 6 Ana    2009    15
#> # … with 1 more row
#> # ℹ Use `print(n = ...)` to see more rows

• Does “Zeta” really occur in 3 different years?

st %>% 
  filter(name == "Zeta") %>%
  group_by(name, year) %>%
  count()
#> # A tibble: 3 × 3
#> # Groups:   name, year [3]
#>   name   year     n
#>   <chr> <dbl> <int>
#> 1 Zeta   2005     8
#> 2 Zeta   2006    23
#> 3 Zeta   2020    23

13.3.5 Other dplyr functions

Our introduction of dplyr in this section only focused on a small set of key functions. Although these functions will suffice for the majority of our daily data transformation tasks, some omissions will briefly be mentioned here.

Merging data tables with *join*()

A limitation of the dplyr functions that we have seen so far is that they all referred to one data table. When we need to combine or merge variables (columns) from two distinct data tables, additional two-table functions are required.

Whenever the two tables contain different cases (rows), simply pasting together the columns of two tables (e.g, by using cbind()) is no longer an option. Instead, we need to recruit some concepts from database management to describe which variables in one table correspond to those of the other table and must specify the particular way in which we want to join the pair of tables. Typical notions occurring in this context are “full join” or “left join”, and terms for set operations like “union”, “intersection”, or “set difference”.

Whereas the base R function merge() can handle many such cases, a dedicated set of dplyr functions containing the keyword join provides tailored solutions to many special cases. See the dplyr vignette on Two-table verbs or Chapter 8: Joining data for an overview of these functions.

Re-naming variables with rename()

When we need to change the names of variables (i.e., of the columns of a data frame or tibble), the rename() function is useful. In its basic form, it uses combinations of new_name = old_name to rename variables. For instance, we could change the status variable to a type variable and simplify two long variable names of the st data as follows:

st |>
  # Rename 3 variables (by new_name = old_name pairs):
  rename(type = status,
         trop_diam = tropicalstorm_force_diameter,
         hurr_diam = hurricane_force_diameter) |>
  # Reduce and print table:
  select(name, year, type, trop_diam, hurr_diam) |>
  slice_sample(n = 10) |> 
  knitr::kable()

name	year	type	trop_diam	hurr_diam
Marilyn	1995	tropical storm	NA	NA
Danielle	1998	hurricane	NA	NA
Henri	1979	tropical depression	NA	NA
Leslie	2018	tropical storm	380	0
Humberto	2013	tropical storm	180	0
Sean	2011	tropical storm	250	0
Dean	1995	tropical depression	NA	NA
Chantal	2001	tropical storm	NA	NA
Bonnie	1998	hurricane	NA	NA
Alicia	1983	tropical depression	NA	NA

Note that we would need to re-assign st (to st itself) to permanently drop the old and keep only the new names.

For changing all variable names of a table in the same fashion, the rename_with() function allows directly applying a function to variable names. For instance, to change all uppercase characters in variable names to lowercase characters, we could use:

# Example:
names(iris)  # contains uppercase names
#> [1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width"  "Species"

# Rename variables by applying a function:
iris |>
  # Apply tolower() to all names:
  rename_with(tolower) |>
  # Print only the names:
  names()
#> [1] "sepal.length" "sepal.width"  "petal.length" "petal.width"  "species"

More complicated re-naming scenarios can specify sets of variables in combination with quantifiers (e.g., see the examples of ?rename() using a lookup vector and the any_of() or all_of() modifiers).

13.3.6 Summary and evaluation

This concludes our summary of essential dplyr functions (Wickham, François, et al., 2023). To sum up:

Summary: Key dplyr functions (Wickham, François, et al., 2023) include:

1. arrange() sorts cases (rows);
2. filter() and slice() select cases (rows) by logical conditions;
3. select() selects and reorders variables (columns);
4. mutate() and transmute() compute new variables (columns) out of existing ones;
5. summarise() collapses multiple values of a variable (rows of a column) to a single one;
   
6. group_by() changes the unit of aggregation (in combination with mutate() and summarise()).

Other useful dplyr functions include variants of rename() and the two-table *join*() functions.

In our evaluation of the pipe operators %>% and |> (in Section 13.2.3 above), we compared their effects to introducing a new notation and emphasized that they provide no new functionality. Similarly, all tasks addressed by dplyr functions could also be performed by clever combinations of base R functions (e.g., by indexing, aggregate(), and tapply()). With respect to the enthusiasm expressed in the quote above (in Section 13.2), this raises the question:

• How can two tools that provide nothing new create something awesome?

Just as we saw for the pipe operator, the beauty and power of dplyr functions derives from their ecological rationality (see Section 1.2.5). Being specifically designed to address simple data transformation tasks, they match the way we usually think about data. Thus, rather than requiring us to re-shape our thinking to the logic of base R, dplyr provides a set of handy tools that aim to do what we want with a minimum of fuzz. While many users find the dplyr functions easier and more natural to use than the corresponding base R functions, which tool we prefer is mostly a matter of experience or of familiarity.

Overall, combining dplyr functions into pipes provides very flexible and powerful tools for transforming (i.e., reshaping and reducing) data. Next, we will encounter additional functions for data transformation from the tidyr package (in Chapter 14). Whereas many of the dplyr pipes of this chapter reduced our data (e.g., when filtering, selecting, or summarizing variables), the primary purpose of tidyr functions is to re-shape data tables into “tidy” data.

13.4 Conclusion

13.4.1 Summary

This chapter first distinguished between two ways of transforming data: Whereas reshaping data changes the form of data, reducing data typically changes both form and content.

We then introduced the %>% operator of the magrittr package (Bache & Wickham, 2022) and its base R cousin |>. Both operators allow chaining sequences of function calls into powerful pipes.

The dplyr package (Wickham, François, et al., 2023) provides a set of useful functions for reshaping and reducing data. In combination with ggplot2 and tidyr, dplyr is a key pillar of the tidyverse (Wickham et al., 2019).

Summary: Data transformation reshapes or reduces data.

The magrittr pipe operator %>% and its base R cousin |> turn nested expressions into sequential expressions (Bache & Wickham, 2022).

Key dplyr functions (Wickham, François, et al., 2023) include:

1. arrange() sorts cases (rows);
2. filter() and slice() select cases (rows) by logical conditions;
3. select() selects and reorders variables (columns);
4. mutate() and transmute() compute new variables (columns) out of existing ones;
5. summarise() collapses multiple values of a variable (rows of a column) to a single one;
   
6. group_by() changes the unit of aggregation (in combination with mutate() and summarise()).

Other useful dplyr functions include variants of rename() and the two-table *join*() functions.

13.4.2 Resources

Here are some pointers to related articles, cheatsheets, and additional links:

Different pipes

For details on and the differences between the magrittr pipe operator %>% and R’s native pipe operator |>, see

• New features in R 4.1.0 (by Russ Hyde, 2021-05-17)

• The new R pipe (by Elio Campitelli, 2021-05-25)

• Differences between the base R and magrittr pipes (by Hadley Wickham, 2023-04-21)

Despite their differences, we can regard both pipe operators as interchangeable for most practical purposes.

On dplyr

• See the cheatsheet on transforming data with dplyr from Posit cheatsheets:

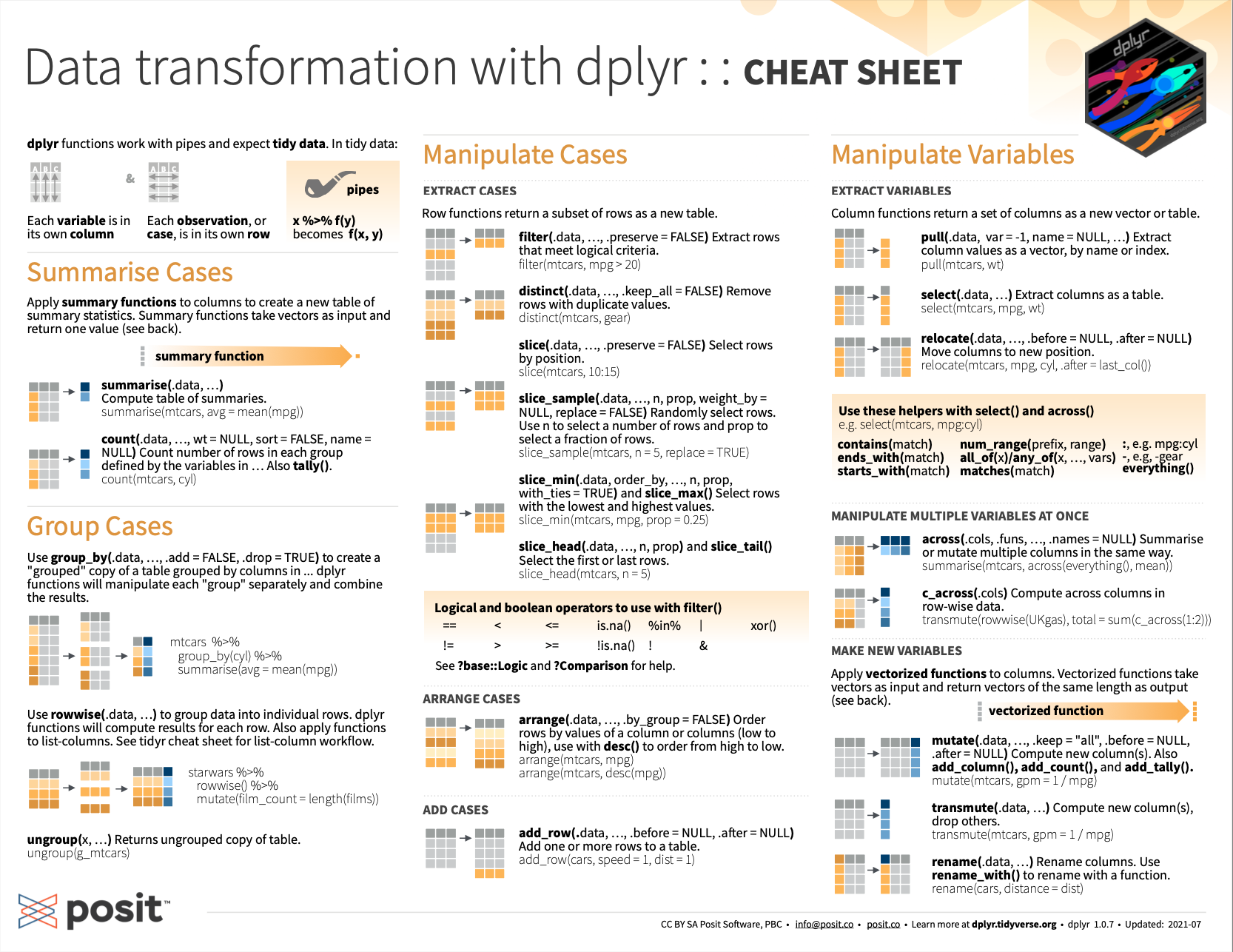
Figure 13.4: Data transformation with dplyr from Posit cheatsheets.

• Introduction on dplyr and pipes: The basics (by Sean C. Anderson, 2014-09-13)

13.4.3 Preview

Having learned how to create data transformation pipes by magrittr and dplyr, the next Chapter 14) on tidying data will expand these skills by adding tools from the tidyr package.

13.5 Exercises

To check our knowledge on dplyr functions and pipes for data transformation, we distinguish between conceptual and practical exercises.

Conceptual exercises

13.5.1 Reshaping vs. reducing data

The essential dplyr functions perform data transformation tasks. Discuss the specific purpose of each function in terms of reshaping or reducing data (as introduced in Section 13.1).

13.5.2 Replacing dplyr functions by base R functionality

Discuss how each of the essential dplyr functions introduced in this chapter could be replaced by using base R functionality.

Hint: As there is no 1:1-correspondence between functions, identify the task performed by each function before thinking about alternative ways of tackling these tasks.

Practical exercises

The following exercises on transforming data with dplyr pipes (Wickham, François, et al., 2023) use a variety of datasets. The links point to corresponding exercises of Chapter 3: Transforming data of the ds4psy book (Neth, 2023a).

13.5.3 Star and R wars

Exercise 2

13.5.4 Sleeping mammals

Exercise 3

13.5.5 Revisiting positive psychology

Exercise 5

13.5.6 Surviving the Titanic

Exercise 6