1.6 Modelos

O comportamento observado do transistor sob as diversas condições de polarização mostradas nas seções anteriores foi modelado ao longo dos anos para retratar as mais diversas características verificadas em laboratório. Não é objetivo aqui detalharmos o histórico e a forma como esses modelos foram construídos. Um dos grupos mais antigos que estudam a modelagem dos MOSFETs é o BSIM (Berkeley Short-channel IGFET Model) (Group 2020) e os modelos listados na Seção 1.1.4 são todos baseados em alguma das versões BSIM.

Os modelos são a forma mais direta de prever o comportamento de um circuito eletrônico antes mesmo que ele seja montado ou fabricado. Foi através da utilização de modelos de simulação que conseguimos tanto projetar novos produtos quanto validá-los preliminarmente antes de sua fabricação. Com isso ganha cedo tempo e economiza-se dinheiro e matérias-primas. A história da evolução dos modelos de dispositivos eletrônicos está intimamente ligada à linguagem Spice que também foi inventada com o mesmo objetivo: facilitar o projeto e teste de circuitos antes de sua fabricação.

Nesse material cobriremos apenas os modelos para pequenos sinais, nas versões mais simples, para dispositivos CMOS: um para baixas frequências e outro para altas frequências, baseados no circuito \(\pi\) simples, também usado para os transistores bipolares.

1.6.1 Baixas Frequências

O modelo de pequenos sinais visa possibilitar o cálculo dos principais parâmetros envolvidos no cálculo das grandezas mensuráveis nos terminais do dispositivo, bem como das principais figuras de mérito envolvendo amplificadores. Vale lembrar que os parâmetros do modelo valem para a linearização feita no ponto de operação em questão. Isto é, qualquer oscilação do ponto de operação poderá mudar substancialmente o valor dos parâmetros de pequenos sinais. Logo, não É vantajoso usar o modelo de pequenos sinais para cálculos manuais e, embora os modelos de simulação sejam mais complexos, é importante que compreendamos a relação dos parâmetros de forma bruta com as grandezas do ponto de operação. Os refinamentos introduzidos pelos modelos de simulação servirão para fazer devidos ajustes ligados a polarização e ao tamanho do dispositivo.

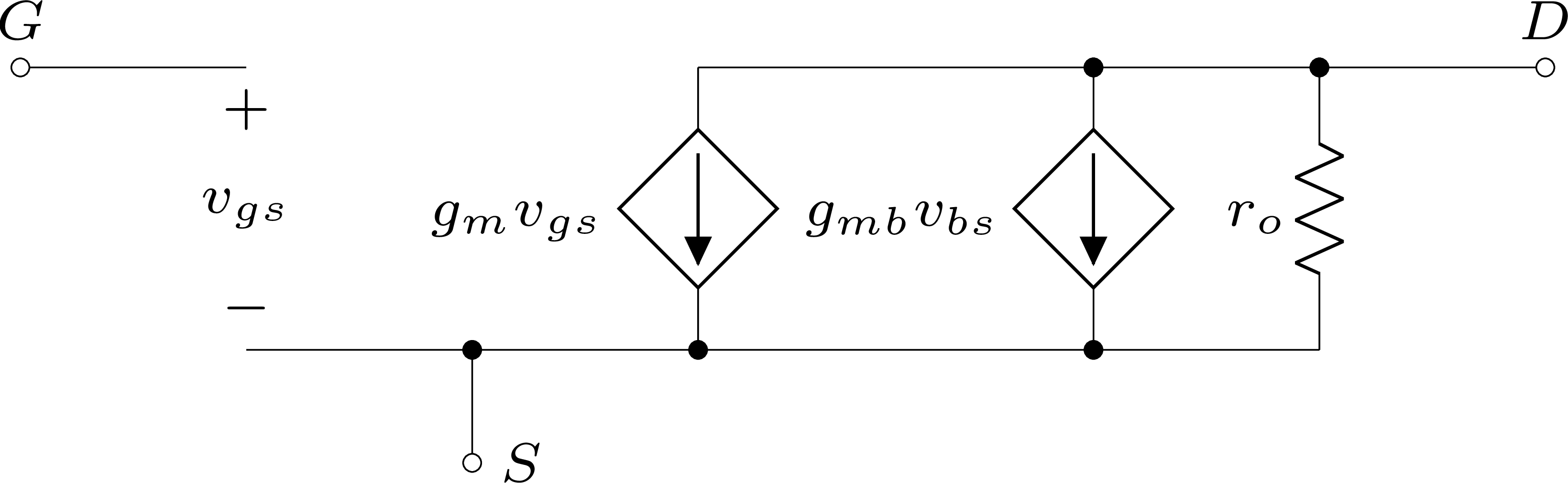
Figura 1.51: Modelo de pequenos sinais de MOSFET para baixas frequências.

A Figura 1.51 contém o modelo de pequenos sinais para baixas frequências contemplando os parâmetros descritos na Seção 1.3. Apenas para lembrar:

• A transcondutância \({g_{m}}\) representa a produção de corrente a partir da tensão de porta, no ponto de operação;

• A transcondutância de corpo \(g_{{m}_{b}}\), idem a \({g_{m}}\), porém para a tensão no terminal de corpo (não representado na figura), relativa ao terminal de fonte, no ponto de operação;

• A resistência de saída \({r_{o}}\) para representar o efeito da modulação do canal com \(V_{DS}\), no ponto de operação;

Esse circuito é válido no ponto de operação (corrente contínua) analisado e todos os seus parâmetros irão variar com esse ponto. Os simuladores de circuitos eletrônicos fazem uso de modelos baseados nesse, conforme dito anteriormente, porém com detalhamento extra, necessário para retratar mudanças que apareceram com a evolução dos processos de microfabricação e o consequente encolhimento dos dispositivos. Os chamados efeitos de canal curto e melhorias que vieram para aumentar a capacidade de integração (de funções), modificaram sobremaneira o funcionamento dos MOSFETs ao longo dos anos de forma que as equações básicas (modelo de segunda ordem) já não conseguem mais retratar um dispositivo real. Contudo, elas são suficientes para que se mostre relações úteis como saber com determinado parâmetro impacta as grandezas mensuráveis e as figuras de mérito de circuitos baseados nesses dispositivos.

1.6.2 Altas Frequências

Quando consideramos o aumento da frequência de trabalho do MOSFET, alguns fenômenos internos começam a aparecer com mais protagonismo, principalmente a própria capacitância de porta. Em resumo, o modelo simplificado que aqui se apresenta terá quatro capacitâncias: uma entre cada dois dos quatro terminais do transistor, como pode ser visto na Figura 1.52. Importante observar que o modelo apresentado na figura contém o modelo de baixas frequências, isto é, o modelo de altas frequências equivale-se ao de baixas frequências se desprezarmos as capacitâncias parasitas.

Figura 1.52: Modelo de pequenos sinais de MOSFET para altas frequências.

Assim, teremos:

• Capacitância porta-fonte, \(C_{gs}\): originalmente representa apenas a capacitância entre o terminal de porta e a fonte do MOSFET. Essa capacitância surge de um dos processos clássicos de microfabricação chamado de “porta autoalinhada” isto é, a posição da porta é quem define as áreas de dreno e fonte. Para garantir que a porta estará sobre o canal, evitando problemas com alinhamento na hora da microfabricação, a dopagem de dreno e fonte é extendida para se encaixar sob o óxido de porta, dando origem à capacitância porta-fonte. Porém, como o terminal de fonte é a referência para que se possa ligar o transistor (\(V_{DS}\) e \(V_{GS}\)), incorpora-se a capacitância porta-corpo \(C_{gb}\) à capacitância porta-fonte. A capacitância porta-corpo é a maior de todas, correspondendo à capacitância do canal. Para a região de saturação de operação, tem-se uma aproximação para o valor dessa capacitância:

\[\begin{equation} C_{gs}= C_{gb}+ C_{gs}' = \dfrac{2}{3}WLC_{ox}+ WL_{ov}C_{ox} \tag{1.4} \end{equation}\]

Em que \(L_{ov}\) é a medida do trespasso (overlap) da porta com dreno e fonte, responsável pela capacitância real porta-fonte: \(C_{gs}'\). O primeiro termo da soma da Equação (1.4) corresponde à capacitância porta-corpo, \(C_{gb}\). Esse trespasso é muito pequeno, chegando a ser menos de 10 % do comprimento do canal. Embora esteja equacionada a capacitância, fica difícil verificar sua validade nos modelos de dispositivos mais complexos. A própria medida \(L_{ov}\) é imprecisa e dependerá muito do processo, da tecnologia e do tamanho ajustado do dispositivo. O importante a se salientar é que a capacitância porta-corpo é a componente principal da entrada do transistor pois é notoriamente maior que a porta-fonte original.

• Capacitância porta-dreno, \(C_{gd}\): formada pelo mencionado trespasso da porta do transistor sobre a região de dreno é tão pequena quanto \(C_{gs}'\). Pensando-se no dispositivo de fato simétrico, a aproximação dessa capacitância é a mesma para \(C_{gs}'\):

\[\begin{equation} C_{gd}= WL_{ov}C_{ox} \tag{1.5} \end{equation}\]

Dessa forma, o polo formado a partir de \(C_{gb}\) será dominante comparado com aquele formado a partir de \(C_{gd}\). Em termos práticos, na região de saturação, \(C_{gb}\) pode ser até mais de duas ordens de graneza maior que \(C_{gd}\).

• Capacitância dreno-corpo, \(C_{db}\): é a capacitância da região de depleção na junção PN formada pelo dreno e o corpo do MOSFET. Dependerá do processo de fabricação (profundidade da junção), do tamanho do dispositivo e da polarização, em especial, da tensão dreno-fonte. Costuma ser na ordem de femto Farads, porém, também dependerá da rótulo da tecnologia. Pode ser ainda menor, dependendo do rótulo: na casa das dezenas de atto Farads.

• Capacitância fonte-corpo, \(C_{sb}\): é a capacitância da região de depleção na junção PN formada pela fonte e o corpo do MOSFET. O seu comportamento e dependências são os mesmos válidos para \(C_{db}\), porém, pelo próprio uso do dispositivo, essa capacitância costuma estar fora de ação em boa parte das utilizações, principalmente porque, mesmo nos circuitos em que há uma difernça entre a tensão de fonte e a tensão de corpo, essa diferença não costuma ser tão significativa.

De qualquer forma, \(C_{db}\) e \(C_{sb}\) são menores até que \(C_{gd}\), sendo muitas vezes desprezadas, já que os seus polos associados são de altíssima frequência, em comparação aos demais.

No próximo capítulo ambos os modelos serão usados para a análise dos amplificadores de estágio simples em baixas e altas frequências.

References

Group, BSIM. 2020. “Berkeley Short-Channel Igfet Model.” University of California, Berkeley. https://bsim.berkeley.edu/.