3.6 Polarização na Fonte

Aqui faremos a junção do amplificador resistivo, visto na Seção 3.3, com a ideia do fonte comum com resistor de fonte, visto na seção anterior. Não usaremos um resistor propriamente dito, mas uma fonte de corrente transistorizada, tal como as já discutidas na Seção 2.2. Para as análises que serão feitas, exacerbou-se a resistência de saída da fonte e sua capacitância equivalente de saída.

Serão elaboradas duas análises: uma para a entrada em modo diferencial e outra para entrada em modo comum. Em cada caso, a operação do circuito será detalhada usando-se como base o circuito exposto na Figura 3.7 a seguir.

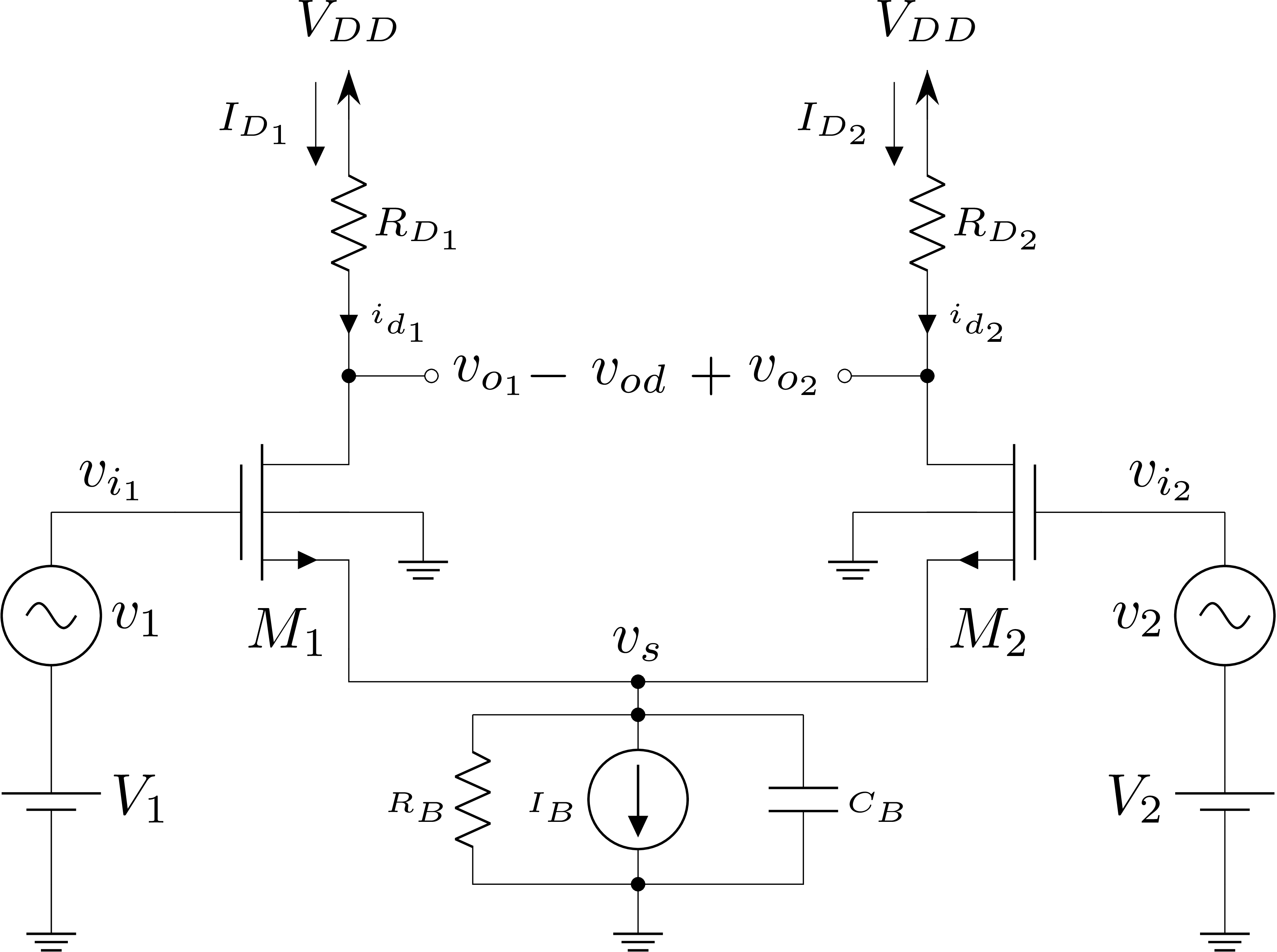
Figura 3.7: Amplificador diferencial com carga passiva - Polarização na fonte.

3.6.1 Entrada em Modo Diferencial

A entrada em modo diferencial prevê que \(v_{i_1}\) e \(v_{i_2}\) são diferentes e portanto gerarão um sinal de entrada \(v_{id}=v_{i_1}-v_{i_2}\), como já apresentado na Seção 3.2.

Os detalhes da operação básica do amplificador diferencial sem a fonte de corrente na fonte já foram discutidos na Seção 3.3. Nos basearemos neles para a análise dessa versão do circuito, que está na Figura ??. Tomando o caso desejado em que ambos os amplificadores fonte comum são idênticos, podemos dizer que a tensão diferencial de entrada \(v_{id}\) será distribuída igualmente entre os dois transistores, levando-nos a considerar que, em termos de pequenos sinais, \(v_{gs_1}=\dfrac{v_{id}}{2}\) e \(v_{gs_2}=-\dfrac{v_{id}}{2}\), para corroborar a expressão de \(v_{id}\).

Com isso em mente e lembrando da equação da corrente de saturação do MOSFET (no modelo de \(2^a\) ordem), podemos dizer que os sentidos das correntes de sinal em \(M_1\) e \(M_2\) serão invertidos:

\[\begin{equation} i_{DS}\ =\ \dfrac{1}{2}\mu C_{ox}\dfrac{W}{L}(v_{gs}-V_{th})^2 \tag{3.19} \end{equation}\]

Sendo as tensões porta-fonte iguais e opostas, então as correntes dreno-fonte também serão iguais e opostas. Ou seja, para o modo de entrada diferencial, a corrente \(i_{d_2}\) na Figura 3.7 estará na verdade indo para \(V_{DD}\) com módulo idêntico ao de \(i_{d_1}\). Esse resultado é muito importante para podermos estalecer que, para a entrada em modo diferencial:

se \(i_{d_1}\) e \(i_{d_2}\) são iguais e com sentidos contrários, ao analisarmos o nó \(v_s\), encontramos que a corrente de sinal que flui entre \(v_s\) e o terra é zero;
logo, não haverá tensão de sinal em \(v_s\);
significando que \(v_s\) será terra de sinal e
o ganho de cada fonte comum será o original da configuração (Equação (3.18).

Em outras palavras, com os amplificadores fonte comum perfeitamente equilibrados, é como se a fonte de corrente de polarização não existisse e nem os seus elementos parasitas. Portanto, não haverá o efeito de redução do ganho para a entrda em modo diferencial.

3.6.2 Entrada em Modo Comum

A entrada em modo comum prevê que \(v_{i_1}\) e \(v_{i_2}\) são iguais entre si ou, numa análise mais genérica, que a sua média aritmética em cada instante seja diferente de zero, conforme as definições traçadas na Seção 3.2.

Sendo as tensões porta-fonte iguais e com mesmo sinal, então as correntes dreno-fonte também serão iguais e com o mesmo sentido. Ou seja, para a entrada em modo comum, a corrente \(i_{d_2}\) na Figura 3.7 estará de fato vindo de \(V_{DD}\) com módulo idêntico ao de \(i_{d_1}\). Isto é, o comportamento do circuito difere da operação em modo diferencial essencialmente por essas correntes. Esse resultado é muito importante para podermos estalecer que, para a entrada em modo comum:

se \(i_{d_1}\) e \(i_{d_2}\) são iguais e com mesmo sentido, ao analisarmos o nó \(v_s\), encontramos que a corrente de sinal que flui entre \(v_s\) e o terra é diferente de zero;
logo, haverá tensão de sinal em \(v_s\);
significando que \(v_s\) não mais será terra de sinal e
o ganho de cada fonte comum será o equivalente ao da versão com resistor de fonte (Equação (3.17).

Em outras palavras, com os amplificadores fonte comum perfeitamente equilibrados, a fonte de corrente de polarização torna-se presente para pequenos sinais, bem como os seus elementos parasitas. Portanto, haverá o efeito de redução do ganho para a entrada em modo comum.

3.6.3 Resumo

Com a introdução da fonte de corrente de polarização da forma exposta na Figura 3.7, conseguimos resolver um dos problemas das topologias sem essa fonte: conseguimos elevar a \(CMRR\) reduzindo o ganho em modo comum frente ao ganho em modo diferencial. Algumas observações importantes sobre o circuito apresentado:

A versão desse mesmo circuito com cargas ativas (como a mostrada na Seção 3.4) poderá apresentar um ganho diferencial ainda maior. Claro que essa elevação de ganho também seria levada ao ganho em modo comum, porém com a possibilidade de se regular a resistência de saída da fonte de corrente para compensar adequadamente essa elevação;
A partir da polarização pode-se controlar as correntes no circuito, modificando \(R_{B}\), \(r_{o_1}\), \(r_{o_2}\) e \(A_{v}\);
A definição do tamanho do transistor de polarização também irá influenciar o tamanho da capacitância equivalente de saída \(C_{B}\), cujo valor influencia a resposta em frequência do circuito (detalhes na Seção 3.7.5);
As dimensões dos transistores também definirão o ponto de flutuação de \(v_s\), \(v_{o_1}\) e \(v_{o_2}\);
O equilíbrio dos fonte comum será importante para definir a influência do efeito de corpo na operação desses amplificadores;
Conseguimos com um único circuito ter ganhos diferentes para os dois tipos de entrada, porém a saída continua sendo diferencial, isto é, precisamos de duas conexões para conseguir o sinal de saída, o que dificulta o acoplamento de estágios simples à saída do diferencial;
E, por fim, sabemos que não é possível que se consiga essa paridade perfeita entre os fonte comum. Dessa forma, poderá haver alguma redução de ganho diferencial, tanto maior quanto maior o desbalanço entre esses amplificadores.