5.3 Malhas Não-Ideias de Realimentação
Nos sistemas analisados anteriormente, a malha de realimentação foi tida como ideal, isto é, não se apresentava como carga nem para a entrada de sinal, na conexão da realimentação, e nem na saída, na medição de sinal. Contudo, é bastante compreensível que, por mais simples que seja a malha de realimentação, não há como ela não drenar nenhuma espécie de corrente para funcionar.
Como exemplo, o clássico circuito do amplificador operacional não-inversor que pode ser visto na Figura 5.13 a seguir.

Figura 5.13: Amplificador Operacional Não-Inversor.
Não é possível imaginar que, quando ligado o circuito, não haja o aparecimento de corrente em \(R_1\) e \(R_2\) até o terra. Certamente irá aparecer corrente e será essa mesma corrente que provocará, em \(R_1\), a tensão de realimentação do circuito. E, a depender do valor das resistências de \(R_1\) e \(R_2\) poderá haver uma corrente não suportada pelo circuito de saída do amplificador operacional. A máxima corrente de saída é um parâmetro presente na folha de dados de qualquer amplificador operacional. Por tudo isso, a escolha da malha de realimentação também define a qualidade da realimentação no que se refere à carga de realimentação introduzida no circuito.
Nessa seção estudaremos como representar malhas não-ideias (reais) de realimentação para facilitar a análise do circuito amplificador realimentado completo, já que não teremos como medir e realimentar de forma ideal.
Pela teoria de circuitos elétricos, qualquer circuito pode ser analisado a partir das suas tensões e correntes, sejam de entrada ou saída. Há como relacionar tensões e/ou correntes num ponto considerado entrada com tensões e/ou correntes em outro ponto considerado como saída. Essa análise pode ser feita com o uso dos quadripolos. Eles são uma forma prática de, não apenas construir essas relações entre as variávies de entrada e de saída, mas também de permitir que separemos as análises: o que é da entrada fica na entrada e o que é da saída, na saída.
Abstraindo-se a análise de circuitos para os amplificadores, eles poderão ser analisados com quaisquer das ferramentas disponíveis. Um amplificador é, antes de tudo, um circuito elétrico. E, como tal, poderá ser analisado de qualquer forma e, portanto, podem ser vistos como quaisquer um dos quatro tipos: tensão, corrente, transimpedância e transadmitância. Aplicando-se esse pensamento ao amplificador operacional não-inversor, podemos analisá-lo para encontrar os quatro tipos de ganho em malha fechada. Só dependerá de definirmos qual é a variável de entrada e qual a de saída.
O circuito da Figura 5.13, quando estudado nos cursos de circuitos elétricos é apresentado com essas condições:
A impedância de entrada do amplificador operacional é ideal para amplificar tensão, ou seja, infinita.
O que leva à consideração de que: não há corrente sendo drenada pelas entradas do amplificador operacional.
Há um “curto-circuito virtual” entre as entradas inversora e não-inversora, o que nos diz que o ganho em malha aberta é infinito.
Para qualquer sinal de entrada, a malha de realimentação não apresenta carga para o amplificador operacional, independente da(s) frequência(s) de trabalho.
Necessariamente é um amplificador de tensão.
Notoriamente, há uma limitação de horizontes para apresentação do circuito e sua consequente análise. É prática para mostrar o amplificador operacional como um elemento de circuito importante e que nos permite fazer muita coisa, contudo, torna-o “mágico” e misterioso. Mas, podemos substituir o amplificador operacional por um circuito equivalente, mesmo que ele conserve as idealidades já relatadas. E, com esse circuito equivalente poderíamos analisar o circuito como qualquer um dos quatro tipos de amplificador.
Para circuitos simples, fica fácil fazer a análise completa do circuito. Para a análise de circuitos mais complexos, essa análise já não é tão simples e aí introduzimos a representação da malha de realimentação por um quadripolo. O quadripolo para representar a realimentação deverá ser escolhido para melhor representar a função da malha de realimentação.
Isto é: como o sinal de realimentação será levado de volta ao circuito e como o sinal de saída será medido na saída.
Assim, cabe repassarmos os quatro tipos de quadripolos e para qual amplificador cada um deles se adequa.
5.3.1 Quadripolo H (Tensão)
A Figura 5.14 mostra uma possível versão desse quadripolo20.
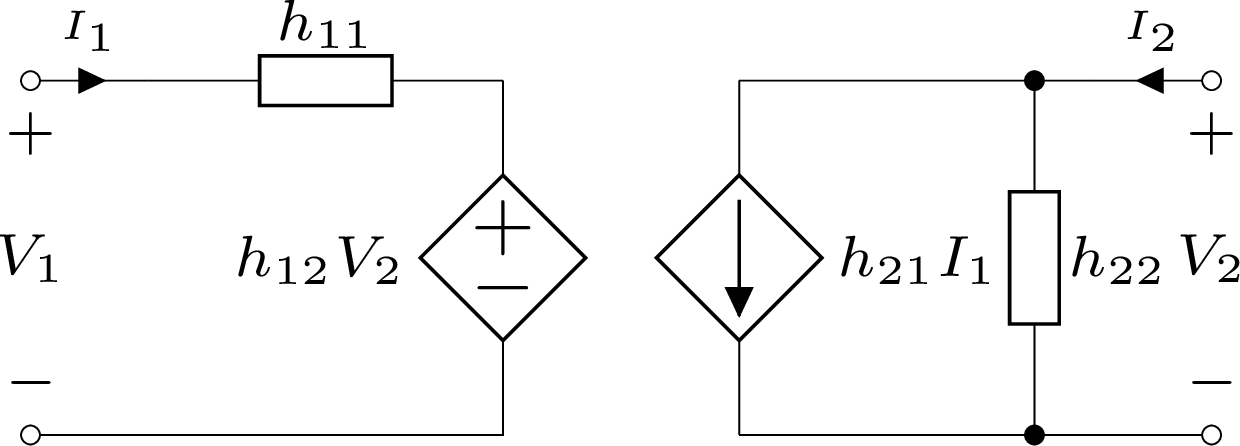
Figura 5.14: Quadripolo H (amplificador de tensão).
Para analisar como esse quadripolo pode representar uma malha de realimentação, vamos começar definindo para quais tipos de sinais ele se adequa e as premissas necessárias para análise.
As premissas que usaremos para esse e demais quadripolos são as seguintes:
A entrada da malha de realimentação está ligada à saída do amplificador;
A saída da malha de realimentação está ligado à entrada do amplificador construindo a realimentação;
Isso nos leva a dizer que \(I_{2}\) e \(V_{2}\) são, respectivamente, corrente e tensão ligados à saída do amplificador e, portanto, relacionadas à medição do sinal de saída. E \(I_{1}\) e \(V_{1}\) são, respectivamente, corrente e tensão ligados à entrada do amplificador, relacionadas à realimentação de sinal.
O parâmetro \(h_{12}\) é responsável por conectar a saída do amplificador de volta à entrada. E \(h_{21}\), por conectar a entrada do amplificador de volta à saída.
A malha \(\beta\) mostrada na Figura 5.8 será substituída tal como vista pelo quadripolo H, tal como visto aqui. Falta explicar por que o quadripolo H é o mais adequado para se analisar amplificadores de tensão. O sinal realimentado precisa ser de tensão o que restringe as opções de quadripolo: H e Z. Isso se deve ao fato notório que não há como subtrair corrente de tensão e vice-versa. Para finalizarmos a análise precisamos considerar a forma de medição do sinal de saída, como já mencionado na Seção 5.2. Para medir tensão, precisamos de um ramo em paralelo, tal como a conexão de um voltímetro. Mede-se tensão com o voltímetro conectado em paralelo ao circuito. Isso nos leva ao quadripolo H que é aquele que tem como variável 1 (saída do quadripolo, no nosso caso) a tensão; e variável 2 (entrada do quadripolo) a corrente.
De forma mais simplificada, estamos usando um quadripolo para modelar o efeito de carga da realimentação no amplificador em malha aberta. O efeito de carga de uma fonte de tensão é dado pela impedância série de saída. O efeito de carga de um voltímetro, ou medidor de tensão, é a sua impedância finita, que estará em paralelo com a saída. Quem modela essa carga da realimentação na medição é o parâmetro \(y_{22}\), em paralelo com a tensão medida. Isso não seria possível no quadripolo Z.
As equações originais do quadripolo H são:
\[\begin{align} h_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{V_{2}=0} \tag{5.18}\\ h_{12}&= \dfrac{V_{1}}{V_{2}}\Bigg|_{I_{1}=0} \tag{5.19}\\ h_{21}&= \dfrac{I_{2}}{I_{1}}\Bigg|_{V_{2}=0}\tag{5.20}\\ h_{22}&= \dfrac{I_{2}}{V_{2}}\Bigg|_{I_{1}=0}\tag{5.21} \end{align}\]
Para as análises que faremos, simplificaremos o uso dos quadripolos da seguinte maneira:
Usaremos os parâmetros do quadripolos tal como se fossem todos impedâncias (ou resistências). Embora não seja estritamente correto da parte de utilização do quadripolo, é prático.
A transmissão direta de sinal da entrada para a saída, proporcionada pelo parâmetro \(x_{21}\) (em que \(x\) pode ser \(h\), \(g\), \(y\) ou \(z\)) será considerada desprezível em comparação com a contribuição da malha aberta. Isto é, dado que a maior parte (quase totatlidade) do sinal de saída é proporcionada pelo amplificador em malha aberta, especialmente nos casos em que seu ganho é muito elevado e a malha de realimentação é formada por elementos passivos.
A primeira simplificação visa apenas a facilitar as análises, principalmente pelo fato de que a maior parte dos usos de malhas de realimentação é para modular o ganho em malha fechada, em que são formadas primariamente por resistores. A última simplificação não poderá ser aplicada a sistemas com uma malha de realimentação ativa que possua ganho acima da unidade e/ou para amplificadores com ganho de malha aberta muito baixo (\(\leq 10\), por exemplo). Decorre da última simplificação que as fontes dependentes associadas à entrada da malha de realimentação serão neutralizadas: as de tensão se tornarão curto-circuitos e as de corrente, circuitos abertos.
Cabe enfatizar também que a simplificação relativa aos parâmetros \(x_{21}\) é apenas na aplicação do circuito para análise e não para o cálculo dos parâmetros do quadripolo.
A partir da primeira simplificação podemos reescrever as equações do quadripolo H como feito a seguir. Atenção especial para \(h_{22}\) que passa a ser uma impedância e não admitância. Também atenção especial que usamos a condição \(I_{1}=0\) para calculá-lo, retirando a influência da fonte dependente do circuito.
\[\begin{align} h_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{V_{2}=0} \tag{5.22}\\ h_{12}&= \dfrac{V_{1}}{V_{2}}\Bigg|_{I_{1}=0} \tag{5.23}\\ h_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{I_{1}=0}\tag{5.24} \end{align}\]
Com essas simplificações, o quadripolo H resume-se ao circuito abaixo, quando aplicado ao circuito do amplificador de tensão:
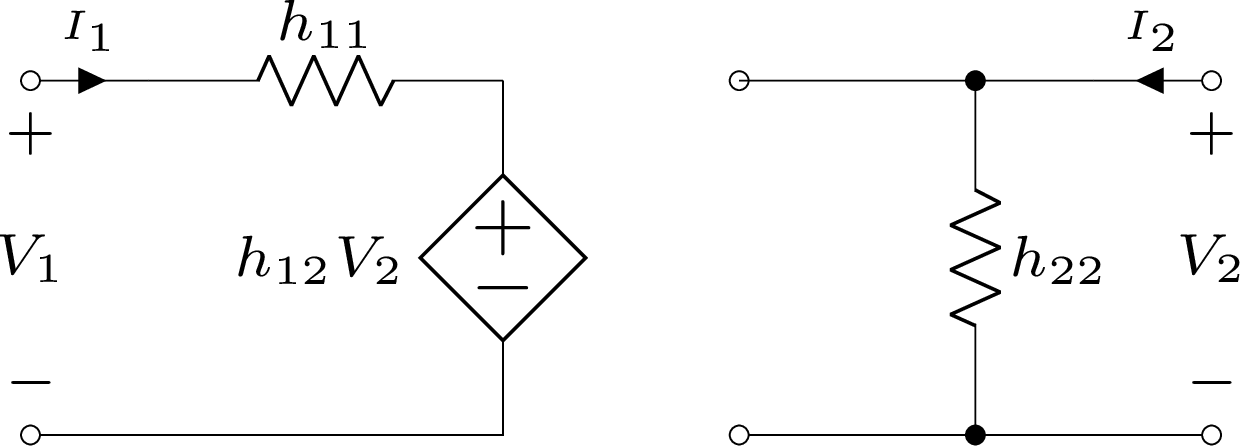
Figura 5.15: Quadripolo H simplificado (amplificador de tensão).
5.3.1.1 Exemplo de uso do quadripolo H
Como forma de entender o uso do quadripolo H, usaremos a mesma malha de realimentação do amplificador operacional não-inversor da Figura 5.13. De forma geral a malha de realimentação será vista como na Figura 5.16 a seguir.
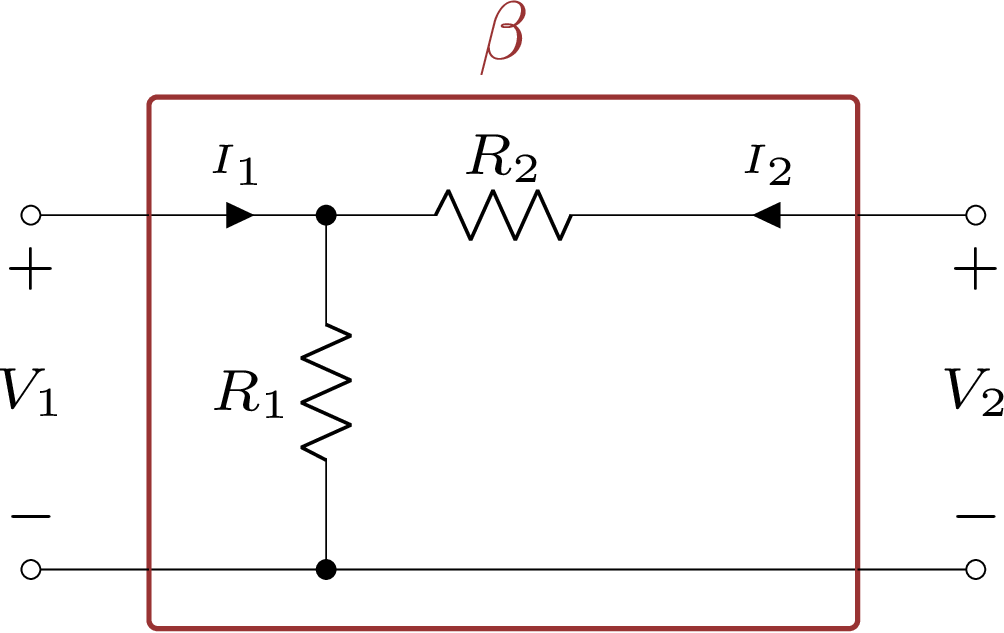
Figura 5.16: Malha de realimentação do Amp. Op. não-inversor.
De acordo com as equações acima, para o cálculo de \(h_{11}\) precisaremos de \(V_{2}=0\) o que leva ao circuito abaixo:
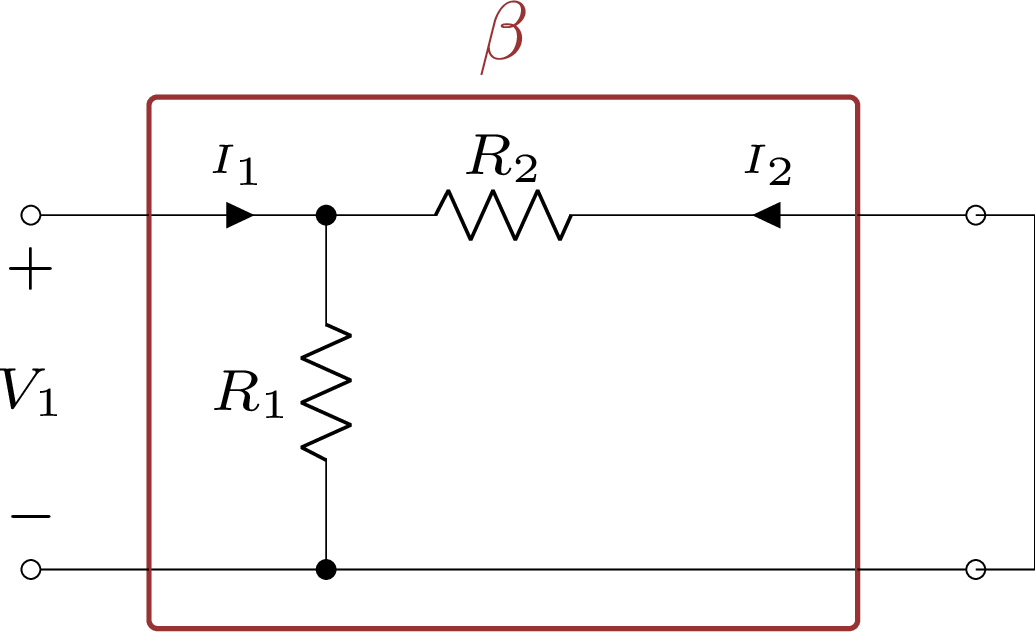
Figura 5.17: Cálculo de \(h_{11}\) para o Amp. Op. não-inversor.
Com o qual calculamos:
\[\begin{equation} h_{11}\ =\ \dfrac{V_{1}}{I_{1}}\ =\ R_1|| R_2 \tag{5.25} \end{equation}\]
Pelo circuito da Figura 5.16, podemos encontrar a relação entre \(V_{1}\) e \(V_{2}\) que é o ganho de realimentação \(\beta\):
\[\begin{equation} h_{12}\ =\ \dfrac{V_{1}}{V_{2}}\ =\ \beta\ =\ \dfrac{R_1}{R_1+ R_2} \tag{5.26} \end{equation}\]
E, também pelo mesmo circuito, finalizamos o cálculo do quadripolo H simplificado para essa malha de realimentação.
\[\begin{equation} h_{22}\ =\ \dfrac{V_{2}}{I_{2}}\ =\ R_1+ R_2 \tag{5.27} \end{equation}\]
Com o circuito calculado, pode-se prosseguir com a análise do amplificador realimentado.
5.3.2 Quadripolo G (Corrente)
O circuito completo do quadripolo G pode ser visto na Figura 5.18 a seguir.
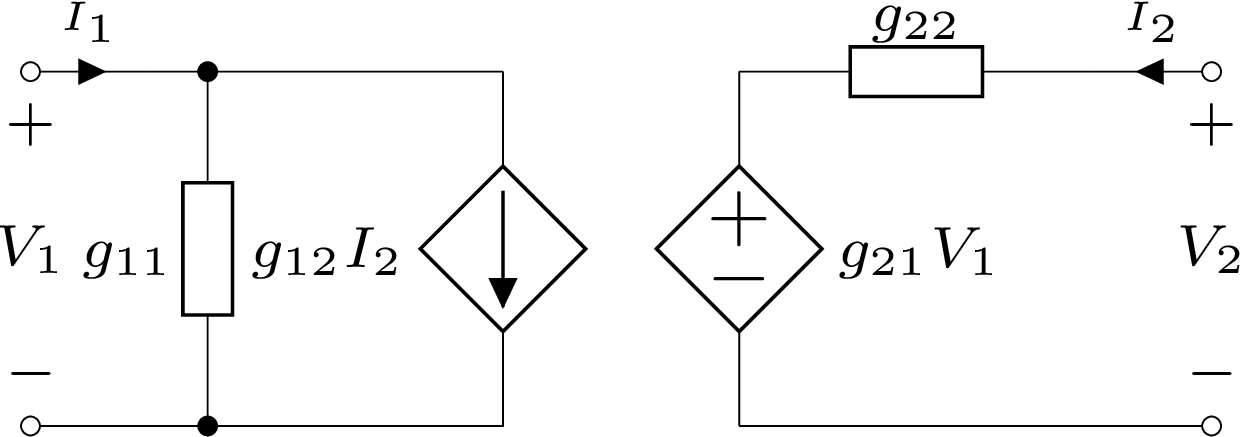
Figura 5.18: Quadripolo G (amplificador de corrente).
E as suas equações originais são:
\[\begin{align} g_{11}&= \dfrac{I_{1}}{V_{1}}\Bigg|_{I_{2}=0} \tag{5.28}\\ g_{12}&= \dfrac{I_{1}}{I_{2}}\Bigg|_{V_{1}=0} \tag{5.29}\\ g_{21}&= \dfrac{V_{2}}{V_{1}}\Bigg|_{I_{2}=0}\tag{5.30}\\ g_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{V_{1}=0}\tag{5.31} \end{align}\]
Percebe-se a sua adequação para o amplificador de corrente pelo fato de que a fonte de saída da realimentação, dada por \(g_{12}I_{2}\), é uma fonte de corrente dependente. O que o difere do quadripolo Y, que também tem uma fonte de corrente na saída da realimentação, é o fato de que o quadripolo G apresenta carga de medição em série, compatível com a medição real de corrente. Como precisamos medir corrente e realimentar corrente, o quadripolo G é o escolhido para a função de modelar a malha de corrente para esse caso.
Aplicando-se as simplificações descritas na subseção anterior, as suas equações serão reescritas dessa forma:
\[\begin{align} g_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{I_{2}=0} \tag{5.32}\\ g_{12}&= \dfrac{I_{1}}{I_{2}}\Bigg|_{V_{1}=0} \tag{5.33}\\ g_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{V_{1}=0}\tag{5.34} \end{align}\]
E o circuito simplificado será:
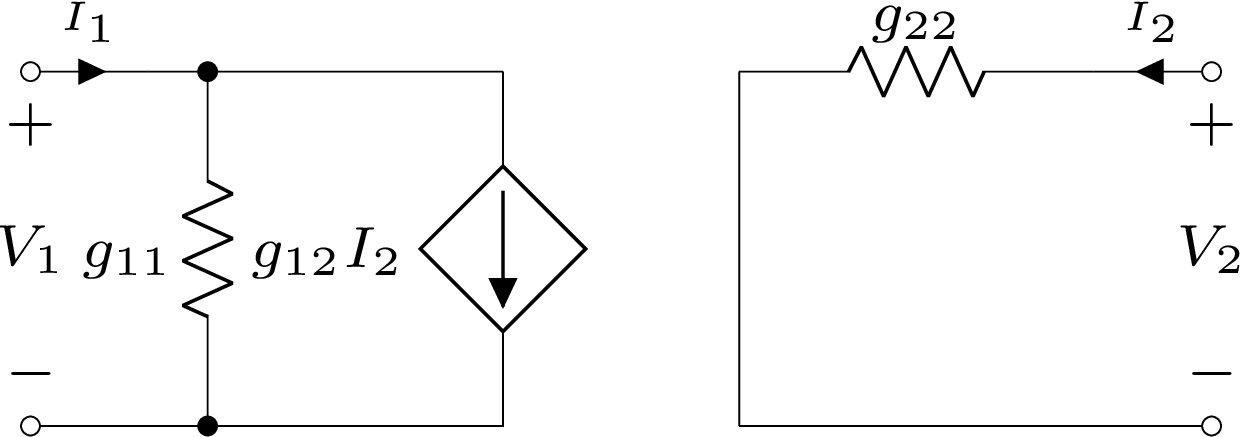
Figura 5.19: Quadripolo G simplificado (amplificador de corrente).
5.3.2.1 Exemplo de uso do quadripolo G
De forma análoga à do quadripolo H, usaremos a mesma malha de realimentação do amplificador operacional não-inversor da Figura 5.13. Usando a malha vista na Figura 5.16 calculamos o parâmetro \(g_{11}\):
\[\begin{equation} g_{11}\ =\ \dfrac{V_{1}}{I_{1}}\ =\ R_1 \tag{5.35} \end{equation}\]
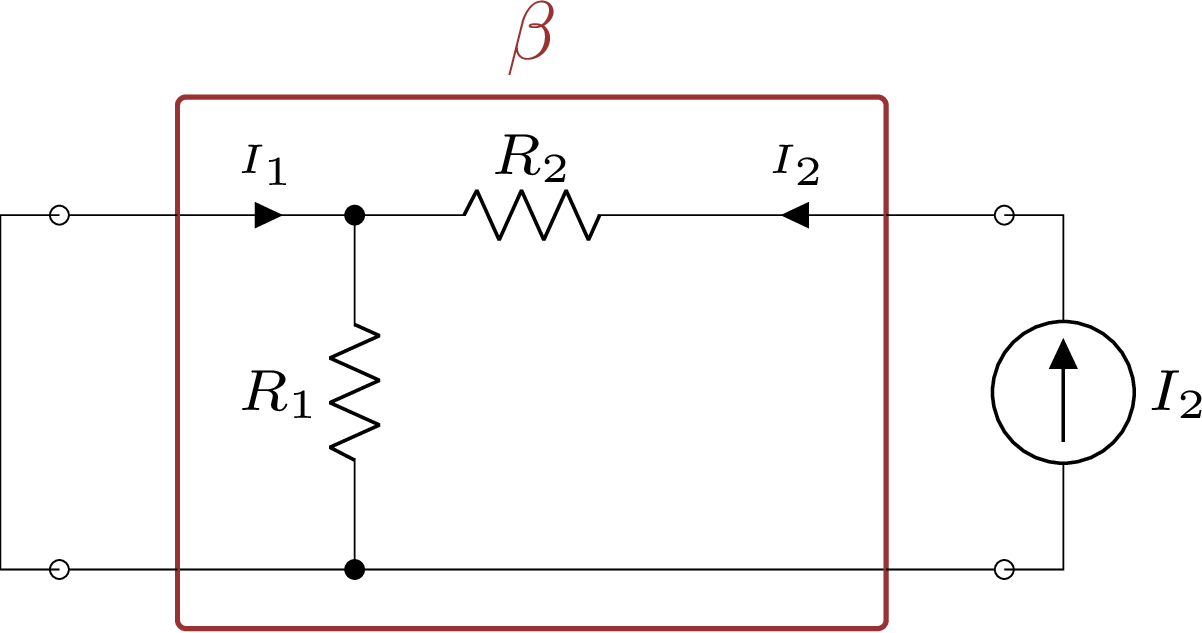
Figura 5.20: Cálculo de \(g_{12}\) para o Amp. Op. não-inversor.
Para o cálculo de \(g_{12}\) forçamos uma corrente na porta 2, tal como na Figura 5.20, e calculamos a relação entre a corrente \(I_{1}\) e a corrente \(I_{2}\):
\[\begin{equation} g_{12}\ =\ \dfrac{I_{1}}{I_{2}}\ =\ \beta\ =\ -1 \tag{5.36} \end{equation}\]
Finalmente, para o cálculo de \(g_{22}\) precisaremos de \(V_{1}=0\) o que leva ao circuito abaixo:
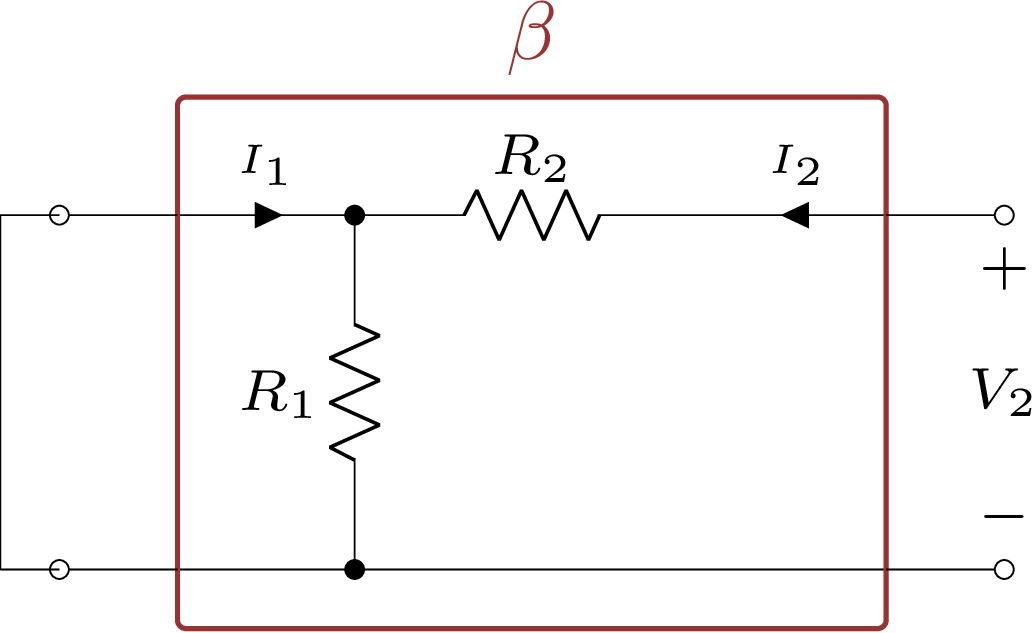
Figura 5.21: Cálculo de \(g_{22}\) para o Amp. Op. não-inversor.
Com o qual calculamos:
\[\begin{equation} g_{22}\ =\ \dfrac{V_{2}}{I_{2}}\ =\ R_2 \tag{5.37} \end{equation}\]
E, dessa forma, finalizamos o cálculo do quadripolo G para a continuidade da análise do amplificador realimentado.
5.3.3 Quadripolo Y (Transimpedância)
Pela Figura 5.22 percebe-se a adequação do quadripolo Y para os amplificadores de transimpedância realimentados pois o ramo paralelo na entrada da realimentação servirá para medir a tensão de saída e realimentá-la na forma de corrente na entrada de sinal.
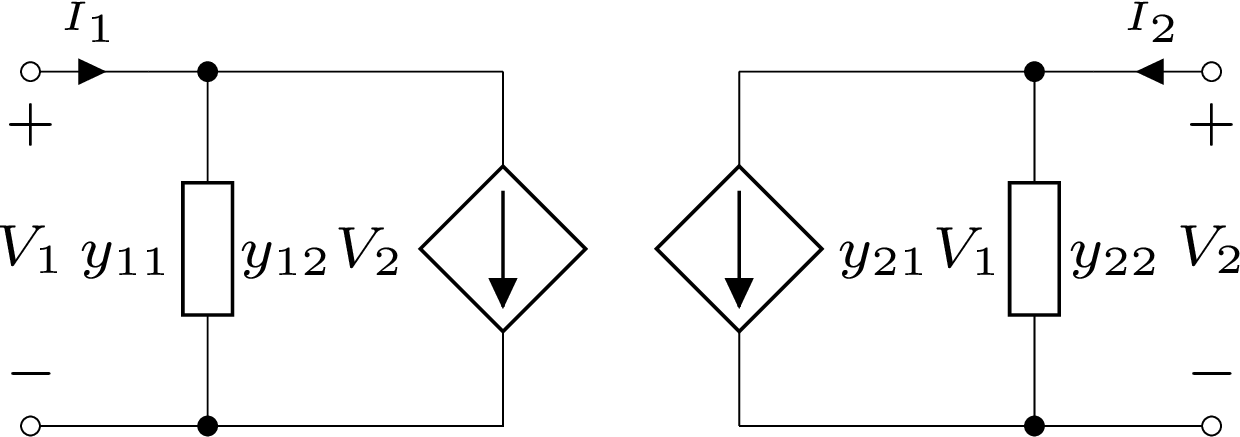
Figura 5.22: Quadripolo Y (amplificador de transimpedância).
As suas equações originais são:
\[\begin{align} y_{11}&= \dfrac{I_{1}}{V_{1}}\Bigg|_{V_{2}=0} \tag{5.38}\\ y_{12}&= \dfrac{I_{1}}{V_{2}}\Bigg|_{V_{1}=0} \tag{5.39}\\ y_{21}&= \dfrac{I_{2}}{V_{1}}\Bigg|_{V_{2}=0}\tag{5.40}\\ y_{22}&= \dfrac{I_{2}}{V_{2}}\Bigg|_{V_{1}=0}\tag{5.41} \end{align}\]
Que, após a aplicação da primeira simplificação tornam-se:
\[\begin{align} y_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{V_{2}=0} \tag{5.42}\\ y_{12}&= \dfrac{I_{1}}{V_{2}}\Bigg|_{V_{1}=0} \tag{5.43}\\ y_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{V_{1}=0}\tag{5.44} \end{align}\]
E o circuito final, após as simplificações será:
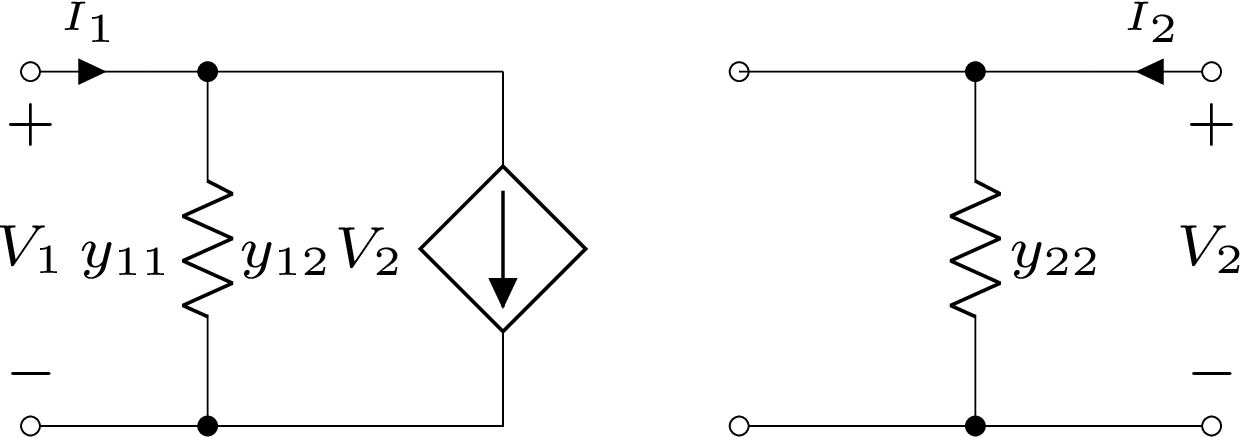
Figura 5.23: Quadripolo Y simplificado (amplificador de transimpedância).
5.3.3.1 Exemplo de uso do quadripolo Y
Para o cálculo do parâmetro \(y_{11}\) usamos um circuito análogo ao de \(y_{11}\), em que \(V_{2}=0\). Por simplicidade, a figura foi reproduzida aqui e a o cálculo de \(y_{11}\) realizado logo em seguida.

Figura 5.24: Cálculo de \(y_{11}\) para o Amp. Op. não-inversor.
\[\begin{equation} y_{11}\ =\ \dfrac{V_{1}}{I_{1}}\ =\ R_1|| R_2 \tag{5.45} \end{equation}\]

Figura 5.25: Cálculo de \(y_{12}\) e \(y_{22}\) para o Amp. Op. não-inversor.
Com base na malha de realimentação vista na Figura 5.25 calculamos o parâmetro \(y_{12}\), com \(V_{1}=0\). O que nos leva a:
\[\begin{equation} y_{12}\ =\ \dfrac{I_{1}}{V_{2}}\ =\ \beta\ =\ -\dfrac{1}{R_2} \tag{5.46} \end{equation}\]
E, com a mesma malha, finalizamos o cálculo dos parâmetros do quadripolo Y ao calcularmos \(y_{22}\):
\[\begin{equation} y_{22}\ =\ \dfrac{V_{2}}{I_{2}}\ =\ R_2 \tag{5.47} \end{equation}\]
E, com o circuito calculado, pode-se prosseguir com a análise do amplificador realimentado.
5.3.4 Quadripolo Z (Transadmitância)
O último quadripolo pode ser visto na Figura 5.26:
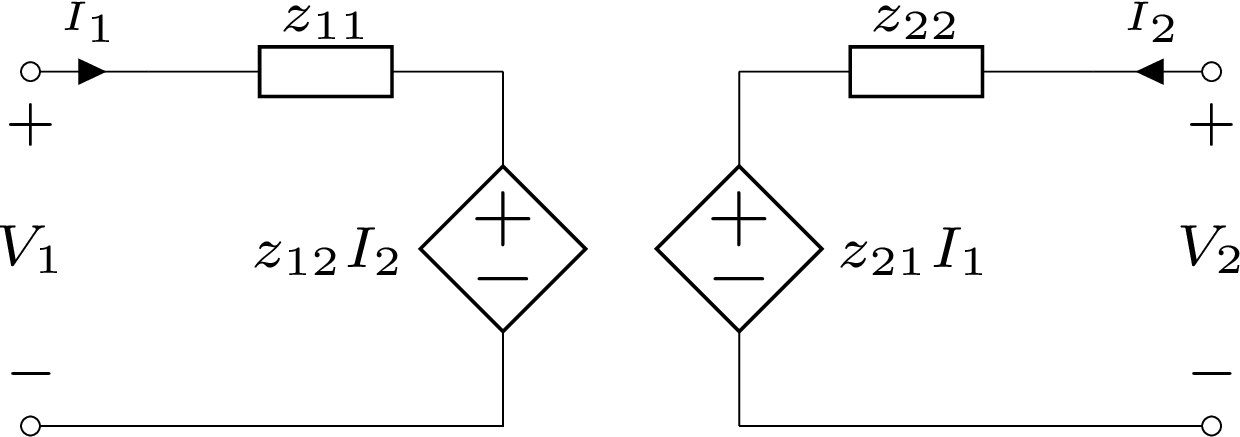
Figura 5.26: Quadripolo Z (amplificador de transadmitância).
Seguindo a lógica usada até então, adequação aos amplificadores de transadmitância realimentados pelo fato de que o ramo série na entrada da realimentação modela a carga da medição em série da corrente de saída do amplificador. E, na outra ponta, na saída da malha de realimentação tem-se uma fonte de tensão dependente dessa mesma corrente medida e que será retornada ao circuito para fechar a malha.
As suas equações originais são:
\[\begin{align} z_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{I_{2}=0} \tag{5.48}\\ z_{12}&= \dfrac{V_{1}}{I_{2}}\Bigg|_{I_{1}=0} \tag{5.49}\\ z_{21}&= \dfrac{V_{2}}{I_{1}}\Bigg|_{I_{2}=0}\tag{5.50}\\ z_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{I_{1}=0}\tag{5.51} \end{align}\]
Que, após a aplicação da primeira simplificação tornam-se:
\[\begin{align} z_{11}&= \dfrac{V_{1}}{I_{1}}\Bigg|_{I_{2}=0} \tag{5.52}\\ z_{12}&= \dfrac{V_{1}}{I_{2}}\Bigg|_{I_{1}=0} \tag{5.53}\\ z_{22}&= \dfrac{V_{2}}{I_{2}}\Bigg|_{I_{1}=0}\tag{5.54} \end{align}\]
Isto é, não há mudanças significativas, ainda que estejamos desprezando a transmissão direta por \(z_{21}\). E o circuito final, após as simplificações será:
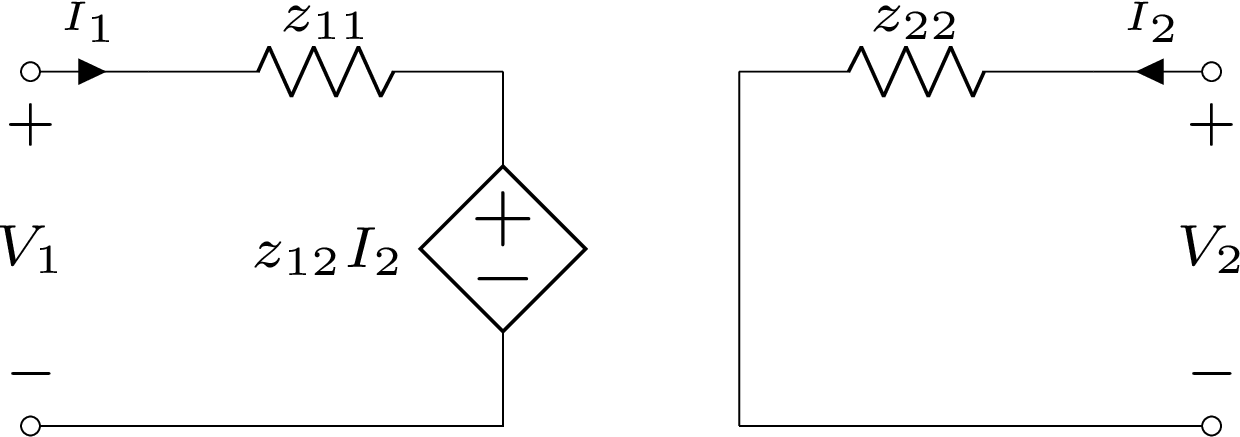
Figura 5.27: Quadripolo Z simplificado (amplificador de transimpedância).
5.3.4.1 Exemplo de uso do quadripolo Z
Para o cálculo do parâmetro \(z_{11}\) usamos o circuito da Figura 5.28. Por simplicidade, a figura foi reproduzida aqui e a o cálculo de \(z_{11}\) realizado logo em seguida.

Figura 5.28: Malha de realimentação do Amp. Op. não-inversor.
\[\begin{equation} z_{11}\ =\ \dfrac{V_{1}}{I_{1}}\ =\ R_1 \tag{5.55} \end{equation}\]
Para o cálculo de \(z_{12}\) forçamos uma corrente na porta 2, tal como na Figura 5.29, e calculamos a relação entre a corrente \(I_{1}\) e a corrente \(I_{2}\):
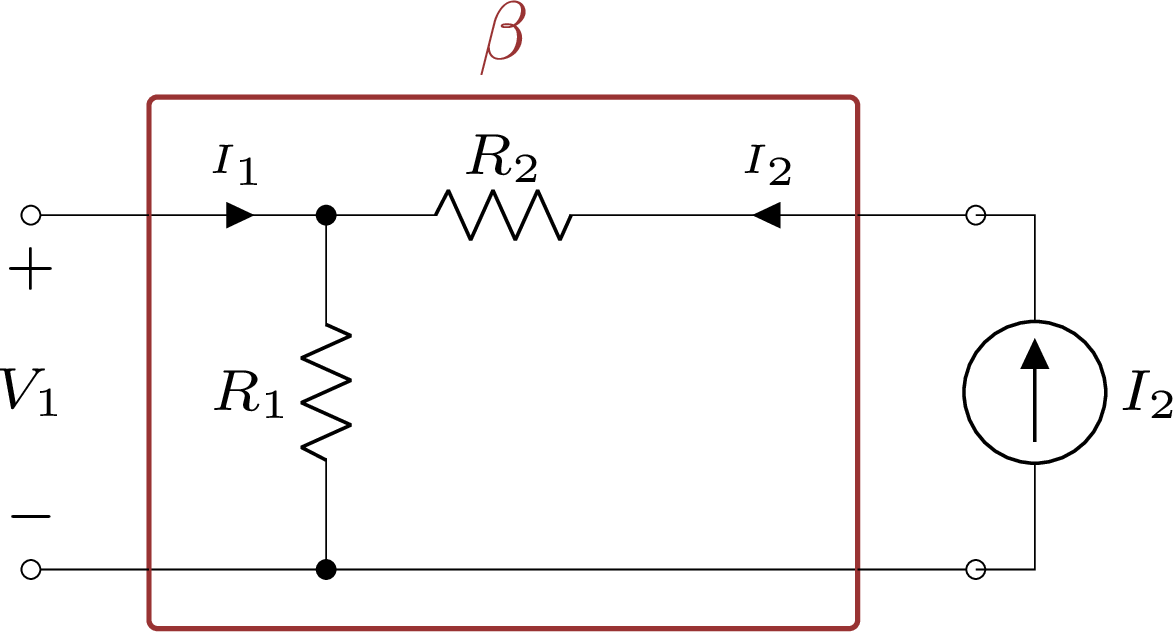
Figura 5.29: Cálculo de \(z_{12}\) para o Amp. Op. não-inversor.
E calculamos:
\[\begin{equation} z_{12}\ =\ \dfrac{V_{1}}{I_{2}}\ =\ \beta\ =\ R_1 \tag{5.56} \end{equation}\]
E, por fim calculamos o parâmetro \(z_{22}\):
\[\begin{equation} z_{22}\ =\ \dfrac{V_{2}}{I_{2}}\ =\ R_1+ R_2 \tag{5.57} \end{equation}\]
E, com o circuito calculado, pode-se prosseguir com a análise do amplificador realimentado.
5.3.5 Observações finais sobre o uso de quadripolos
Em qualquer dos casos estudados anteriormente, o uso dos quadripolos facilita a análise pois separa claramente o circuito de saída do amplificador do circuito de entrada, porém mantendo a análise ampla o suficiente para dar conta dos efeitos da realimentação, tanto os desejados quanto os não desejados.
Foi dito que qualquer circuito amplificador pode ser analisado de qualquer das quatro perspectivas. Contudo, quando usamos os quadripolos estamos forçando um tipo de análise e, nem todas as malhas de realimentação se enquadrarão perfeitamente no estudo. Essa análise sob qualquer perspectiva só será possível se considerarmos o circuito completo. Como será visto nas próximas seções, poderá haver casos em que o uso do quadripolo inviabilisa a análise de um amplificador em mais de um tipo.
Antes de prosseguirmos com essa análise, vamos olhar para a Tabela 5.3.
| Parâmetro | Amp. Tensão (H) | Amp. Corrente (G) | Amp. Transimpedância (Y) | Amp. Transadmitância (Z) |
|---|---|---|---|---|
| \(x_{11}\) | \(R_1|| R_2\) | \(R_1\) | \(R_1|| R_2\) | \(R_1\) |
| \(x_{12}\) | \(\dfrac{R_1}{R_1+ R_2}\) | \(-1\) | \(-\dfrac{1}{R_2}\) | \(R_1\) |
| \(x_{22}\) | \(R_1+ R_2\) | \(R_2\) | \(R_2\) | \(R_1|| R_2\) |
É possível perceber, pela tabela resumo dos exemplos de uso dos quadripolos, que o quadripolo G não é adequado para se analisar o amplificador operacional não-inversor. Isso se deve ao fato de que \(g_{12}=-1\), um valor constante, que não faz sentido para análise de qualquer amplificador realimentado. Como já se conhece da teoria básica de circuitos, alterar os valores de \(R_1\) e \(R_2\) irá provocar alterações na malha de realimentação e, portanto, no ganho em malha fechada. Um ganho de realimentação igual a \(-1\), fixo, certamente não traduz isso. As variações nos valores de \(R_1\) e/ou \(R_2\) precisam aparecer no ganho de realimentação, tal como acontece com os demais parâmetros: \(h_{12}\), \(y_{12}\) e \(z_{12}\).
Por fim, vê-se que a mesma malha de realimentação irá apresentar uma forma de carregamento diferente, tanto na entrada quanto na saída do amplificador, dependendo de que sinais foram escolhidos para análise.
Há diversas formas de se representar as tensões e correntes, tanto nas polaridades e sentidos quanto nos nomes utilizados para representá-los.↩︎