2.3 Fonte Comum

A primeira configuração de amplificador simples que veremos é a fonte comum. Como o próprio nome da configuração diz o terminal de fonte é o ponto comum entre a entrada na porta e a saída no dreno. Nas Figuras 2.21 e 2.22 pode-se ver as versões com carga resistiva do fonte comum com NMOS e PMOS como amplificador, respectivamente.

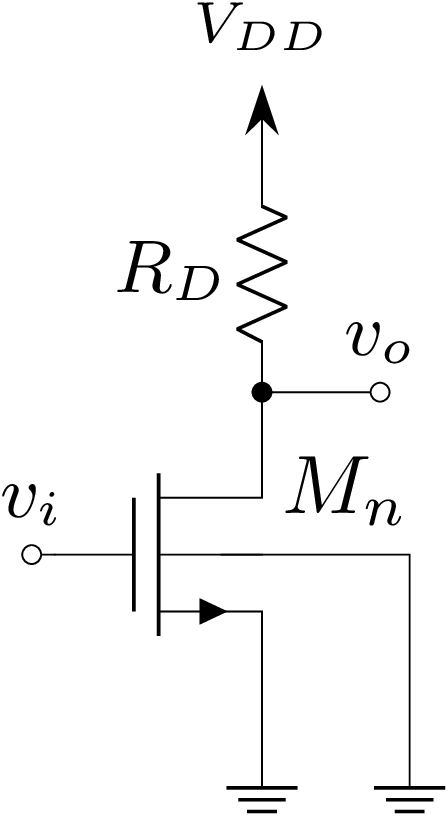
Figura 2.21: Fonte comum NMOS com carga resistiva.

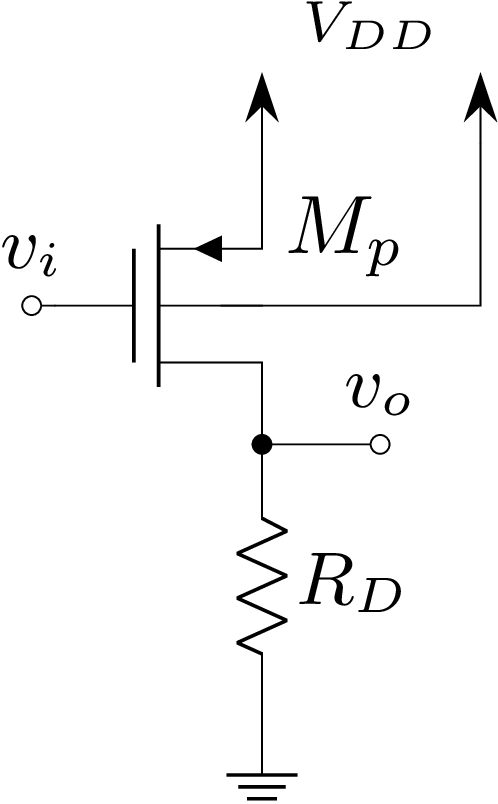
Figura 2.22: Fonte comum PMOS com carga resistiva.

Embora já tenhamos visto que a carga resistiva não será mais usada, começaremos com a versão mais simples para que se entenda a versão final, com carga ativa provida por espelho de corrente. Para iniciarmos a análise dos circuitos acima vamos lembrar primeiro ou circuito equivalente de pequenos sinais de um MOSFET, para baixas frequências, que pode ser encontrado na Figura 2.23. Lembre-se que o circuito equivalente serve para ambas as polaridades. Os parâmetros mostrados na figura podem ser relembrados na Seção 1.3. Embora o terminal de corpo não esteja evidenciado na figura, nela podemos notar o seu efeito através da transcondutancia de corpo \(g_{{m}_{b}}\).

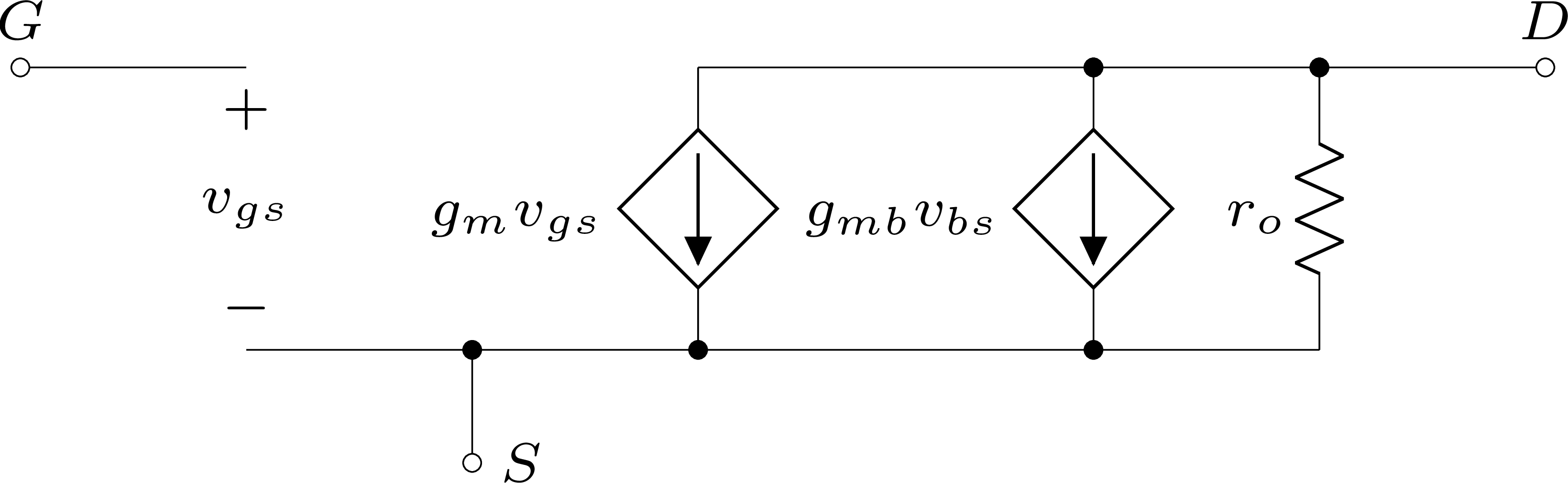
Figura 2.23: Modelo de pequenos sinais de um MOSFET para baixas frequências.

É preciso lembrar também que modelo de pequenos sinais se refere a um único ponto de operação, isto é, o transistor encontra-se devidamente polarizado (\(V_{GS}\)) e conduzindo uma corrente constante (\(I_{DS}\). Nesse ponto de operação fácil uma linearização da resposta corrente de saída vs. tensão de entrada, em que os parâmetros de pequenos sinais são obtidos. Com esse modelo de pequenos sinais em mente e adicionando o resistor de carga, podemos chegar ao circuito equivalente de pequenos sinais para o amplificador fonte comum. E ele pode ser visto na Figura 2.24. No circuito a carga \(R_{D}\) está representada pelo resistor \(R_{A}\) e os motivos para isso serão explicados adiante.

Figura 2.24: Modelo de pequenos sinais de um fonte comum para baixas frequências.

Como essa é a primeira análise o modelo de pequenos sinais apresentados foi mantido na Figura 2.24 a fonte independente relativa a transcondutancia de corpo. Analisando-se as Figuras 2.21 e 2.22 fica evidente que atenção corpo fonte (\(v_{bs}\)) é zero, anulando o efeito dessa fonte para esse circuito. Vale recordar também que na análise de pequenos sinais todas as fontes contínuas não contribuem para a formação de sinal: as fontes de tensão contínua serão curto-circuitadas e as de corrente serão abertas. Por isso o resistor \(R_{A}\) está ligado entre o dreno e o terra. Como corpo e fonte estão no terra de sinal, isso significa que \(R_{A}\) e \({r_{o}}\) estão em paralelo, o que foi evidenciado no circuito da Figura 2.25.

Figura 2.25: Modelo de pequenos sinais de um fonte comum para baixas frequências: rearranjo das cargas.

Substituindo os dois resistores em paralelo por \({R_{o}}\) e levando em conta que \(v_{bs}\) é zero, chegamos ao circuito final do fonte comum para pequenos sinais em baixas frequências:

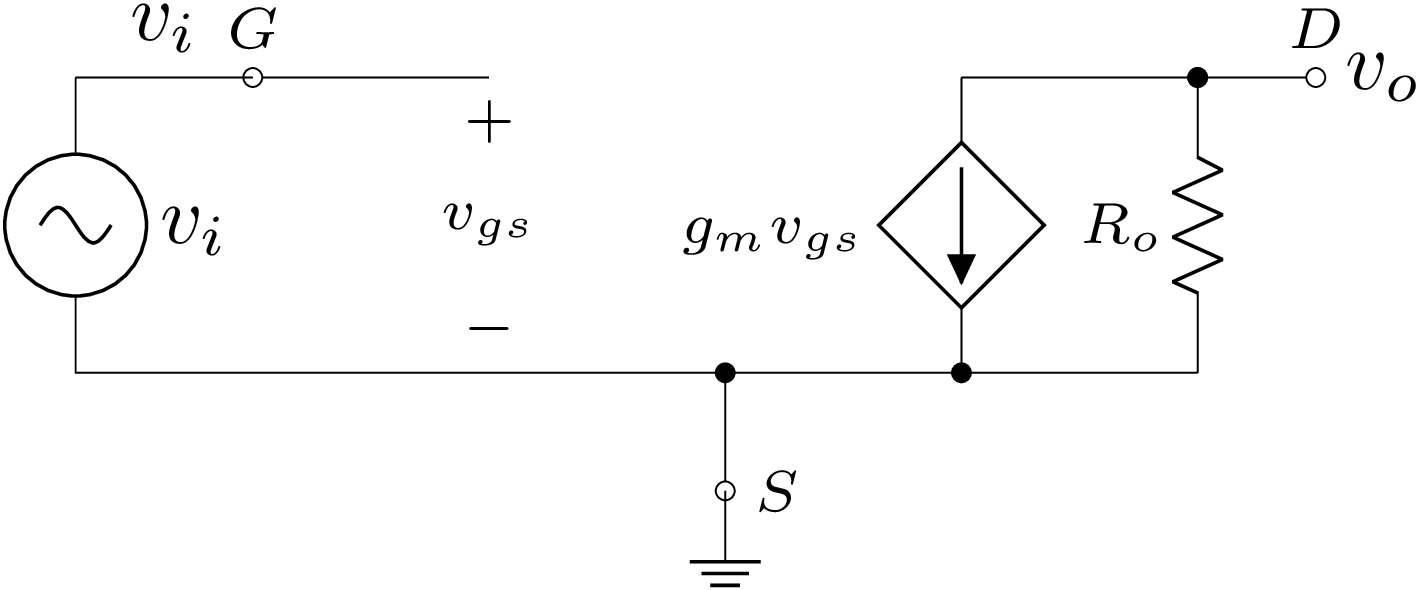
Figura 2.26: Modelo de pequenos sinais de um fonte comum para baixas frequências: circuito final.

Analisando-se o circuito da Figura 2.26 podemos chegar ao ganho de tensão do fonte comum:

\[\begin{align} v_{o}&= -{g_{m}}v_{gs}{R_{o}}\\ v_{o}&= -{g_{m}}v_{i}{R_{o}}\\ \dfrac{v_{o}}{v_{i}} &= A_{v}= -{g_{m}}{R_{o}}\\ A_{v}\ &= -{g_{m}}({r_{o}}|| R_{A}) \\ \tag{2.5} \end{align}\]

Se considerarmos a carga do circuito \(R_{D}\), então a Equação (2.5) torna-se idêntica à Equação (2.1), que foi mostrada na Seção 2.1 para compararmos o amplificador com carga resistiva coom aquele com carga ativa.

Dessa equação já tiramos duas conclusões importantes sobre esse amplificador: ele inverte a fase do sinal de tensão sendo amplificado e, a depender da polarização ajustada, pode ter ganhos elevados. Elevado para versões CMOS significa que pode chegar até a \(300\ V/V\) ou até um pouco mais, dependendo das dimensões do transistor. Para transistores bipolares, consegue-se chegar acima dos \(700\ V/V\).

2.3.1 Carga Ativa

Como já visto na Seção 2.1 a versão do fonte comum com a carga ativa apresenta um transistor operando como fonte de corrente. A forma simplificada desse amplificador pode ser vista nas Figuras 2.27 e 2.28 tendo um NMOS e um PMOS como amplificador, respectivamente.

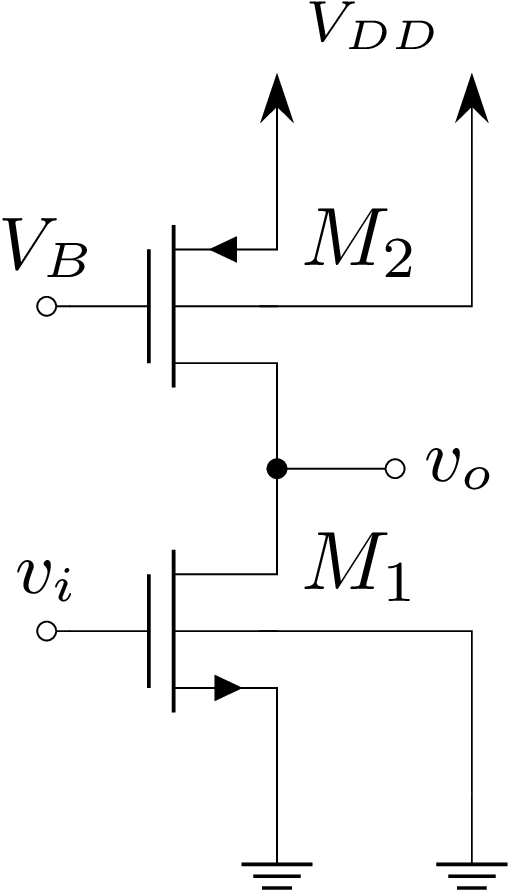
Figura 2.27: Fonte comum NMOS com carga ativa - versão simplificada.

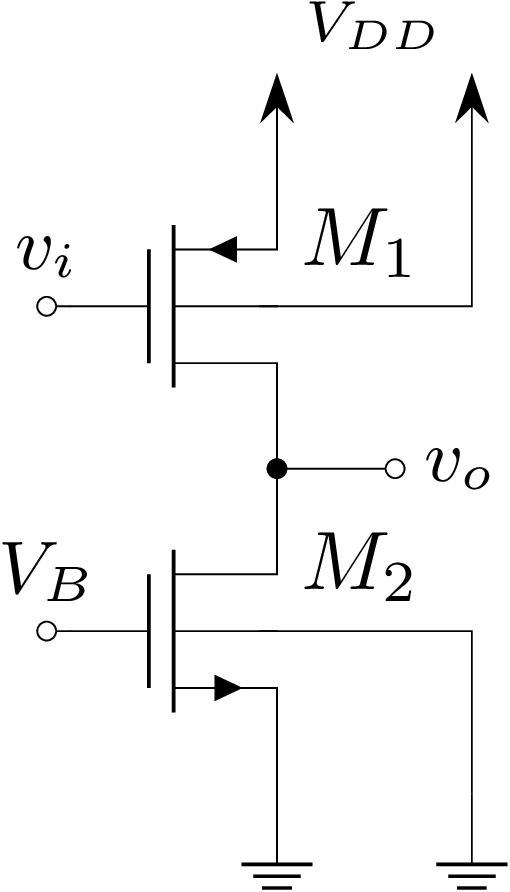
Figura 2.28: Fonte comum PMOS com carga ativa - versão simplificada.

Também naquela sessão foi discutido que é necessário o ajuste da tensão \(V_{B}\) para que o transistor de carga comporte-se na maneira desejada. O que faremos agora é analisá-lo do ponto de vista dos pequenos sinais, tendo como base a Figura 2.23 aplicado ao transistor \(M_{2}\) das figuras anteriores. Os terminais de fonte e corpo estão no mesmo potencial, logo a fonte de corrente dependente de \(g_{{m}_{b}}\) não está ativa no circuito. Como \(V_{DD}\) é uma tensão contínua então fonte de curto estarão no terra de sinal. O terminal de porta recebe uma tensão contínua (\(V_{B}\)) e, portanto, em termos de pequenos sinais a porta de \(M_{2}\) também estará aterrada, o que neutraliza a outra fonte de corrente dependente. Assim, o que sobra do modelo de pequenos sinais para o transistor de carga ativa é tão somente a resistência de saída \({r_{o_2}}\), que estará conectada entre o dreno e fonte, que é terra de sinal. Isso significa que o circuito equivalente do fonte comum com carga ativa é o mesmo da versão com carga resistiva, trocando-se apenas qual é o resistor de carga.

Uma outra forma de ver isso é substituir nas Figuras 2.21 e 2.22 a carga resistiva pelo equivalente funcional do transistor das Figuras 2.27 e 2.28. Isso resultaria nos circuitos das Figuras 2.29 e 2.30 logo a seguir.

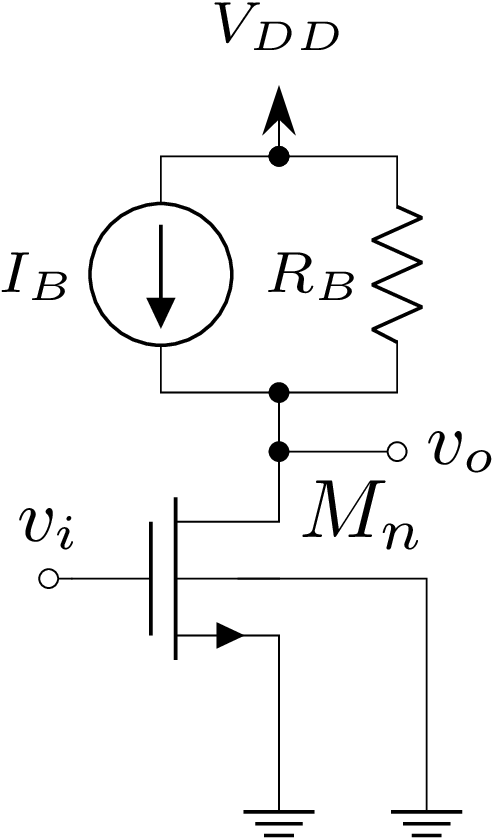
Figura 2.29: Fonte comum NMOS com carga ativa - versão com fonte de corrente.

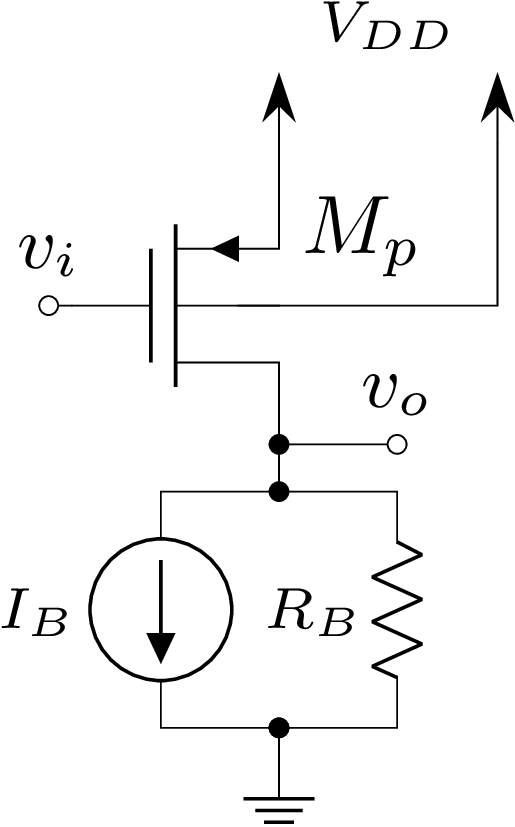
Figura 2.30: Fonte comum PMOS com carga ativa - versão com fonte de corrente.

Se formos analisar esses circuitos com as regras para pequenos sinais, a fonte de corrente será aberta e restará no circuito apenas a sua resistência de saída que, nesse caso, é a resistência de saída do transistor de carga ativa, como visto na Seção 2.2. E chegaríamos ao mesmo circuito equivalente de pequenos sinais também por esse caminho.

Conclusão: as principais diferenças, em termos de comportamento em pequenos sinais, entre a carga ativa e a carga passiva são:

• o valor da resistência de carga: uma é do resistor \(R_{D}\) e a no outro caso, será relativa ao transistor de carga ativa;

• o valor da transcondutância, que pode ser até mais elevado na versão ativa que na versão passiva.

A expressão de ganho da Equação (2.5) permanece a mesma e a carga genérica \(R_{A}\) do circuito da Figura 2.24 será agora \({r_{o_2}}\).

Por fim, podemos pensar na fonte corrente das Figuras 2.29 e 2.30 sendo implementadas com os espelhos de corrente vistos na Seção 2.2, mais precisamente nas Figuras 2.17 e 2.16, respectivamente. Se fizermos a devida substituição chegamos ao circuito completo do amplificador fonte comum com carga ativa nas versões NMOS, Figura 2.31, e PMOS, Figura 2.32.

Figura 2.31: Fonte comum NMOS com carga ativa - circuito completo.

Figura 2.32: Fonte comum PMOS com carga ativa - circuito completo.

As ligações do terminal de corpo dos transistores foram omitidas por simplicidade. O circuito é dito um amplificador simples pois há apenas um transistor amplificador (\(M_{1}\)). O transistor \(M_{2}\) é a carga do amplificador \(M_{1}\) e o transistor \(M_{R}\) está no circuito para fornecer a tensão de referência para a porta de \(M_{2}\), ou ainda, a corrente de referência para um amplificador já que \(M_{2}\) é espelho da corrente de referência.

2.3.2 Resistências de Entrada e de Saída

Para fecharmos as análises sobre um amplificador fonte comum faltam as resistências de entrada e saída. Começamos com a mais simples de analisar que é a resistência de entrada, a qual consideraremos como infinita. Mesmo que haja uma corrente de porta não zero, ela é muito pequena e será desprezada, o que faz com que \(R_{in}=\infty\).

Análise de resistência de saída é feita da seguinte forma:

• a entrada do circuito deve ser nula para que não interfira na análise e

• aplica-se uma fonte de teste \(V_{X}\) no terminal de saída do amplificador, sendo a resistência de saída a resultante da expressão:

\[\begin{equation} R_{out}\ =\ \dfrac{V_{X}}{I_{X}} \tag{2.6} \end{equation}\]

Para calcularmos a resistência de saída do fonte comum tomaremos por base o circuito da Figura 2.26. Ao anularmos a fonte de tensão de entrada, automaticamente anulamos a fonte de corrente dependente, restando no circuito apenas \({R_{o}}\), que é o paralelo de \({r_{o}}\) e \(R_{A}\). Assim, se aplicarmos a fonte de tensão de teste no terminal de saída, a resistência vista por essa fonte é \({R_{o}}={r_{o}}||R_{A}\). E, pelo que foi analisado anteriormente para o ganho, é uma impedância de saída alta (\(> 100\ k\Omega\)), principalmente para a versão do amplificador com carga ativa.

2.3.3 Modelo para Altas Frequências

O conceito de alta frequência obviamente é relativo. Uma frequência será considerada alta quando as reatâncias capacitivas associadas àquelas que compõem o modelo do MOSFET para altas frequências (Seção 1.6.2) tornam-se significativas em relação às resistências de entrada e de saída do amplificador para baixas frequências. Ou ainda, de maneira mais completa, quando o valor das impedâncias de entrada e saída do amplificador começa a ser alterado devido ao aumento da frequência. O modelo mais completo é o de altas frequências, de forma que a análise das impedâncias de entrada e saída (próxima seção), também ajudam a definir a “alta frequência” de cada amplificador. A variação no ganho do amplificador com a frequência é consequência direta dessa variação das impedâncias de acoplamento. Isso irá modificar a operação amplificador e analizar as modificações na operação é o objetivo dessa seção. É extremamente importante salientar o quanto a polarização do amplificador influencia toda a análise que será feita aqui e para as impedâncias.

A análise em altas frequências será aqui detalhada apenas para a versão com carga ativa do amplificador fonte comum, uma vez que ela é mais complexa que a análise da versão com carga resistiva. Para a análise do amplificador em altas frequências, faremos uso do modelo de pequenos sinais descrito na Seção 1.6.2. Contudo, antes de aplicarmos o modelo de pequenos sinais é importante que identifiquemos quais das quatro capacitâncias de cada transistor envolvido no circuito estará de fato ativa quando do aumento de frequência.

Para tanto, uma versão simplificada do circuito do amplificador foi elaborada para mostrar essas capacitâncias e ela pode ser conferida nas Figuras 2.33 e 2.34 para o NMOS e PMOS, respectivamente.

Figura 2.33: Fonte comum NMOS com carga ativa - versão simplificada - altas frequências.

Figura 2.34: Fonte comum PMOS com carga ativa - versão simplificada - altas frequências.

Como o transistor amplificador tem os terminais de fonte e corpo no mesmo potencial, a capacitância \(C_{sb_1}\) não estará ativa e, portanto, não faz parte do circuito. Essa é a mesma justificativa para que \(C_{gs_2}\) e \(C_{sb_2}\) também não estejam no circuito. Lembrando que \(V_{B}\) é terra de sinal da mesma forma que \(V_{DD}\). A parte do amplificador responsável pela geração da corrente de referência não foi adicionada pelo mesmo fato que também não foi levada em consideração para baixas frequências: não contribui para a formação de sinal, logo, esse fato não se altera pela variação de frequência.

Para a análise de resposta em frequência do circuito, iremos fazer uma fusão do circuito de pequenos sinais para baixas frequências da Figura 2.26 e acrescentaremos as capacitâncias mostradas nas Figuras 2.33 e 2.34. O resultado pode ser conferido na Figura 2.35 a seguir:

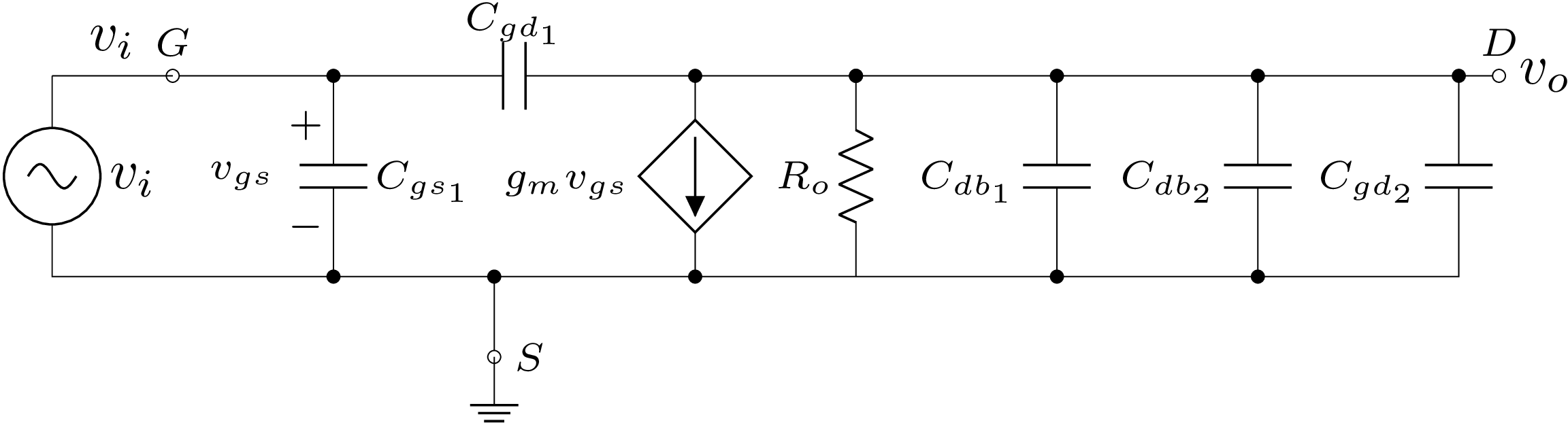
Figura 2.35: Modelo de pequenos sinais do fonte comum para altas frequências.

Cabe simplificar o circuito anterior admitindo as capacitâncias acopladas à saída como uma só, que chamaremos \(C_{o}=\). Dessa forma:

\[C_{o}\ =\ C_{db_1}||C_{db_2}||C_{gd_2}\ =\ C_{db_1}+C_{db_2}+C_{gd_2}\] Com a essa simplificação podemos chegar ao circuito final para análise, que é o da Figura 2.36:

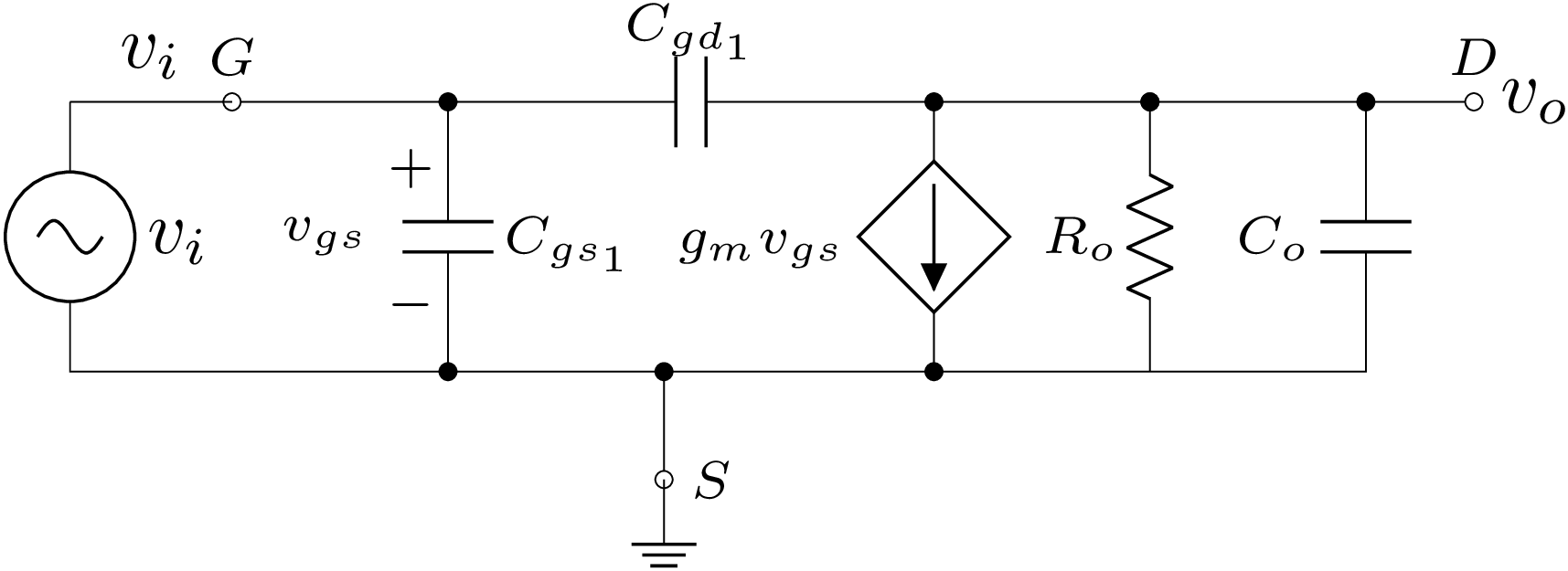
Figura 2.36: Modelo final de pequenos sinais do fonte comum para altas frequências.

Baseando-se nesse circuito, podemos escrever a equação para a Lei de Kirchhoff para as correntes no nó \(v_{o}\), usando-se as simplificações introduzidas pela variável s da transformada de Laplace:

\[\begin{equation} C_{gd_1}s(V_{i}-V_{o}) =\ {g_{m}}V_{i}+ \dfrac{V_{o}}{Z_{o}} \tag{2.7} \end{equation}\]

Em que \(Z_{o}={R_{o}}||\dfrac{1}{sC_{o}}=\dfrac{{R_{o}}}{s{R_{o}}C_{o}+ 1}\). Nessa equação e nas próximas em que usamos a variável de Laplace, as tensões e correntes aparecerão em letras miúsculas, indicando que trata-se de uma versão abreviada dessas grandezas no domínio da frequência. Isto é, está implicito que \(V_{i}=V_{i}(s)\) e \(V_{o}=V_{o}(s)\), por exemplo. Desenvolvendo a equação anterior:

\[\begin{align} C_{gd_1}sV_{o}+ \dfrac{V_{o}}{Z_{o}} &= C_{gd_1}sV_{i}- {g_{m}}V_{i}\\ V_{o}\left(C_{gd_1}s + \dfrac{1}{Z_{o}}\right) &= V_{i}\left(C_{gd_1}s - {g_{m}}\right) \\ V_{o}\left(\dfrac{Z_{o}C_{gd_1}s + 1}{Z_{o}}\right) &= V_{i}\left(C_{gd_1}s - {g_{m}}\right) \\ \dfrac{V_{o}}{V_{i}} = A_{v}(s)&= \dfrac{Z_{o}(C_{gd_1}s - {g_{m}})}{Z_{o}C_{gd_1}s + 1} \\ A_{v}(s)&= \dfrac{{R_{o}}(C_{gd_1}s - {g_{m}})}{{R_{o}}C_{gd_1}s + {R_{o}}C_{o}s + 1}\\ A_{v}(s)&= \dfrac{{R_{o}}(C_{gd_1}s - {g_{m}})}{{R_{o}}(C_{gd_1}+ C_{o})s + 1} \tag{2.8} \end{align}\]

Embora já seja algum avanço na análise, vê-se que a capacitância de porta \(C_{gs_1}\) não entra na expressão anterior, o que precede de uma simplificação feita até então: o sinal de entrada está aplicado diretamente à porta do transistor amplificador. Sabemos que não é plausível que essa impedância de porta não seja influente no circuito. Sabemos também que não é possível esse tipo de acoplamento: sempre haverá uma impedância de acoplamento entre a fonte de sinal e o amplificador. Contudo, muitas vezes é interessante que se separe o que é do amplificador com o que pertence à fonte de sinal e à carga. Carga essa que foi considerada ideal para tensão: infinita. O que também sabemos não ser possível.

Uma diferenciação importante, que se faz aqui nesse texto, com relação à grande maioria dos demais livros de Eletrônica é essa separação. Principalmente para a análise de impedâncias de entrada e saída. Considera-se aqui não fazer sentido a inclusão das impedâncias de fonte e carga ao amplificador na análise completa uma vez que essa análise fica amarrada à fonte e à carga incluídas na análise. Para que se mude a fonte e/ou a carga, será preciso recalcular o circuito. Por isso, até então, não foi feito isso para a análise do ganho e das impedâncias em baixas frequências.

Contudo, ao se utilizar o amplificador de forma prática sempre haverá as referidas impedâncias: acoplamento da fonte e de carga, ainda que essa seja a ponta de prova do instrumento de medição do sinal. Assim, faremos a inclusão da resistência de fonte na análise do amplificador em altas frequências. Ela será a responsável por compor o divisor de tensão para o MOSFET em altas frequências. Sem ela, a entrada será aplicada diretamente a \(C_{gs_1}\) o que diferencia o acoplamento apenas em corrente, mas não em tensão. E, em termos de circuito, não seria possível determinar a corrente da fonte \(v_{i}\), pelo menos não com o que foi feito até agora.

O circuito equivalente não será redesenhado para incluirmos uma resistência \(R_{sig}\) entre a fonte de sinal \(v_{sig}\) e o amplificador. Com a inclusão dessa resistência, poderemos escrever duas equações para a Lei de Kirchhoff das correntes: uma no nó de entrada (porta) e outra para o nó de saída, que já está pronta na Equação (2.7). Para o nó de entrada, teremos:

\[\begin{equation} \dfrac{V_{sig}-V_{i}}{R_{sig}} = C_{gd_1}s(V_{i}-V_{o}) + C_{gs_1}sV_{i} \tag{2.9} \end{equation}\]

Na obtenção da Equação (2.8) tem-se a relação pura entre \(V_{i}\) e \(V_{o}\). Ao substituirmos \(V_{i}\) na Equação (2.9) a partir dessa relação com \(V_{o}\) vinda da Equação (2.8), chegamos à função de transferência do fonte comum, quando há uma resistência de acoplamento entre a fonte de sinal e o amplificador:

\[\begin{equation} A_v \ = \ \dfrac{V_{o}}{V_{sig}}\ =\ \dfrac{-{g_{m}}{R_{o}}\left(1-\dfrac{C_{gd_1}}{{g_{m}}}s\right)}{as^2+bs+1} \tag{2.10} \end{equation}\]

Em que:

• \(a = {R_{o}}R_{sig}[C_{o}(C_{gd_1}+C_{gs_1})+C_{gs_1}C_{gd_1}]\)

• \(b = R_{sig}[C_{gd_1}(1+{g_{m}}{R_{o}})+C_{gs_1}]+{R_{o}}(C_{gd_1}+C_{o})\)

Percebe-se agora o efeito de \(C_{gs_1}\) e o impacto direto de \(R_{sig}\) na faixa de passagem do amplificador. Em quaisquer dos casos, com ou sem a \(R_{sig}\) no circuito, é perceptível também o efeito da polarização e do tamanho do dispositivo na faixa de passagem do amplificador.

Importante notar que o fonte comum tem um zero no semi-plano direito, \(\omega _z = \dfrac{{g_{m}}}{C_{gd_1}}\), o que leva o sistema a se comportar como um sistema de fase não-mínima. Esse tipo de sistema não é instável, por si, mas pode levar à instabilidade quando em malha fechada. Para maiores detalhes sobre sistemas de fase não-mínima, pode-se consultar esse vídeo ou esse artigo. Uma outra forma de perceber isso é que o referido zero contribuirá da mesma forma que um zero negativo para a magnitude da resposta do sistema, mas oferecerá um atraso extra de fase perto de sua frequência, o que pode reduzir a margem de fase, principalmente se esse zero estiver em frequências próximas dos polos. Isso pode ocorrer com dispositivos grandes operando com baixa transcondutância, por exemplo.

Outro ponto importante para se observar é que não foi tratado o efeito de uma carga qualquer externa ao amplificador. Isso por que seu efeito se dará na mudança de \({R_{o}}\) que passaria a contar com essa impedância em paralelo.

Por fim, mas não menos importante, é possível verificar que o ganho em corrente-contínua (baixas frequências ou \(s=0\)) é idêntico ao calculado anteriormente (Equação (2.5)).

2.3.4 Impedâncias de Entrada e de Saída

Agora que já passamos pela análise para altas frequências do amplificador, temos como avançar o modelo completo para aumentarmos a previsibilidade das análises, mesmo que não se tenha uma impedância de acoplamento da fonte de sinal (\(R_{sig}\)) considerável (não desprezível). Para analisarmos as impedâncias de entrada e saída, usaremos as mesmas regras já expostas na Seção 2.3.2. Para as análises das impedâncias usaremos o circuito final da análise em altas frequências exposto na Figura 2.36. Para a impedância de entrada \(Z_{in}\) tomaremos a fonte de teste \(V_{X}\) acoplada diretamente ao nó \(v_{i}\). Na entrada teremos:

\[\begin{equation} I_{X}= C_{gs_1}V_{X}s + C_{gd_1}(V_{X}-V_{o})s \tag{2.11} \end{equation}\]

E, no nó de saída:

\[\begin{equation} C_{gd_1}(V_{X}-V_{o})s = {g_{m}}V_{X}+ \dfrac{V_{o}}{Z_{o}} \tag{2.12} \end{equation}\]

No processo de análise, pode-se desevolver a Equação (2.12) para que possamos escrever \(V_{o}\) em função de \(V_{X}\). Ao fazê-lo chegamos a:

\[\begin{equation} V_{o}= \dfrac{Z_{o}(sC_{gd_1}-{g_{m}})}{Z_{o}C_{gd_1}s+1}V_{X} \tag{2.13} \end{equation}\]

Substituindo-se a Equação (2.13) e a expressão para \(Z_{o}\) na Equação (2.12) e fazendo-se os devidos arranjos, chega-se a:

\[\begin{equation} Z_{in}(s) = \dfrac{{R_{o}}(C_{gd_1}+C_{o})s+1}{{R_{o}}[C_{o}(C_{gs_1}+C_{gd_1})+C_{gs_1}C_{gd_1}]s^2+({g_{m}}{R_{o}}C_{gd_1}+C_{gs_1}+C_{gd_1})s} \tag{2.14} \end{equation}\]

Em termos práticos, para baixas frequências (\(s=0\)) teremos:

\[\begin{equation} \lim_{s \to 0} Z_{in}(s) = \infty \tag{2.15} \end{equation}\]

E, para altas frequências (\(s \to \infty\)) teremos:

\[\begin{equation} \lim_{s \to \infty} Z_{in}(s) = 0 \tag{2.16} \end{equation}\]

Os resultados das Equações (2.15) e (2.16) são compatíveis com o que já se esperava da observação do circuito. Para baixas frequências consideramos a entrada como sendo perfeitamente isolada. E, ao observarmos o circuito para altas frequências (Figura 2.36), em altas frequências a reatância de \(C_{gs_1}\) tenderá a um curto-circuito, de forma que impedância de entrada realmente irá a zero.

Para a impedância de saída, com base no mesmo circuito, lembrando que a entrada deve ser anulada, podemos escrever a equação no nó de saída:

\[\begin{equation} I_{X}= C_{gd_1}V_{X}s + \dfrac{V_{X}}{Z_{o}} \tag{2.17} \end{equation}\]

Resolvendo essa equação podemos chegar a:

\[\begin{equation} Z_{out}(s) = \dfrac{{R_{o}}}{{R_{o}}(C_{gd_1}+C_{o})s+1} \tag{2.18} \end{equation}\]

Em termos práticos, para baixas frequências (\(s=0\)) teremos:

\[\begin{equation} \lim_{s \to 0} Z_{out}(s) = {R_{o}} \tag{2.19} \end{equation}\]

E, para altas frequências (\(s \to \infty\)) teremos:

\[\begin{equation} \lim_{s \to \infty} Z_{out}(s) = 0 \tag{2.20} \end{equation}\]

Esses resultados também estão de acordo com as análises realizadas anteriormente.

2.3.5 Operação em Altas Frequências: Cálculo vs Simulação

Na seção 2.3.3 foi detalhado o comportamento do amplificador fonte comum sob altas frequências. Nessa seção usaremos o simulador e as funções de transferência para verificar o resultado obtido com um e outro na análise dos amplificadores. O amplificador é o mesmo usado na comparação entre a carga passiva e a ativa feita na Seção 2.1. A comparação será feita da seguinte forma:

1. Realização da simulação com análise na frequência no ponto de operação usado como referência;
2. Extração dos parâmetros de pequenos sinais dos transistores, amplificador e de carga ativa;
3. Utilização dos parâmetros da simulação para cálculo das funções de transferência obtidas na Seção 2.3.3;
4. Tabelamento dos parâmetros de interesse obtidos da simulação e do cálculo:
   1. Ganho em corrente contínua;
   2. Frequência de corte;
   3. Frequência de ganho unitário;
   4. Polos e zeros do sistema.

Os códigos de simulação no NGSpice estão detalhados na próxima seção, bem como os códigos do Octave¹⁰, software usado para traçar o diagrama de Bode a partir das funções de transferência calculadas.

A Figura 2.37 contém a saída da simulação do NGSpice para o amplificador sem \(R_{sig}\). O módulo da função de transferência pode ser visto na Figura 2.38 e a fase, na Figura 2.39.

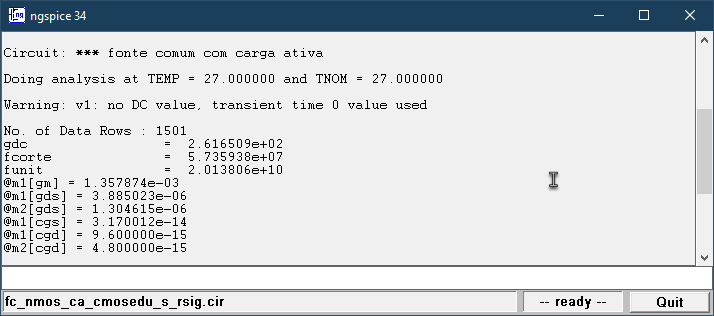
Figura 2.37: Fonte comum: log do NGSpice com resultados da simulação AC. Sem \(R_{sig}\).

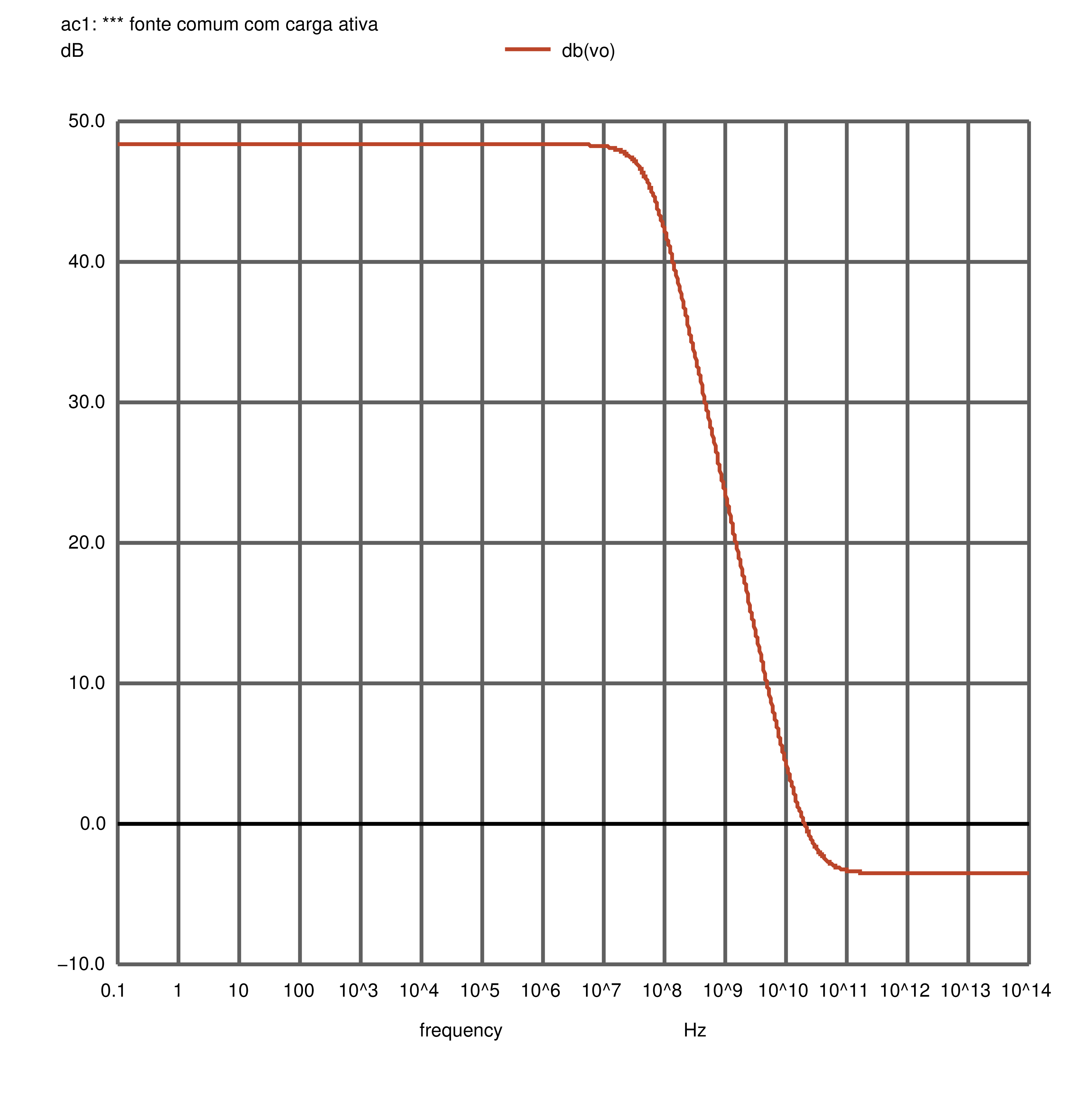
Figura 2.38: Fonte comum: módulo da resposta em frequência, resultado da simulação AC. Sem \(R_{sig}\).

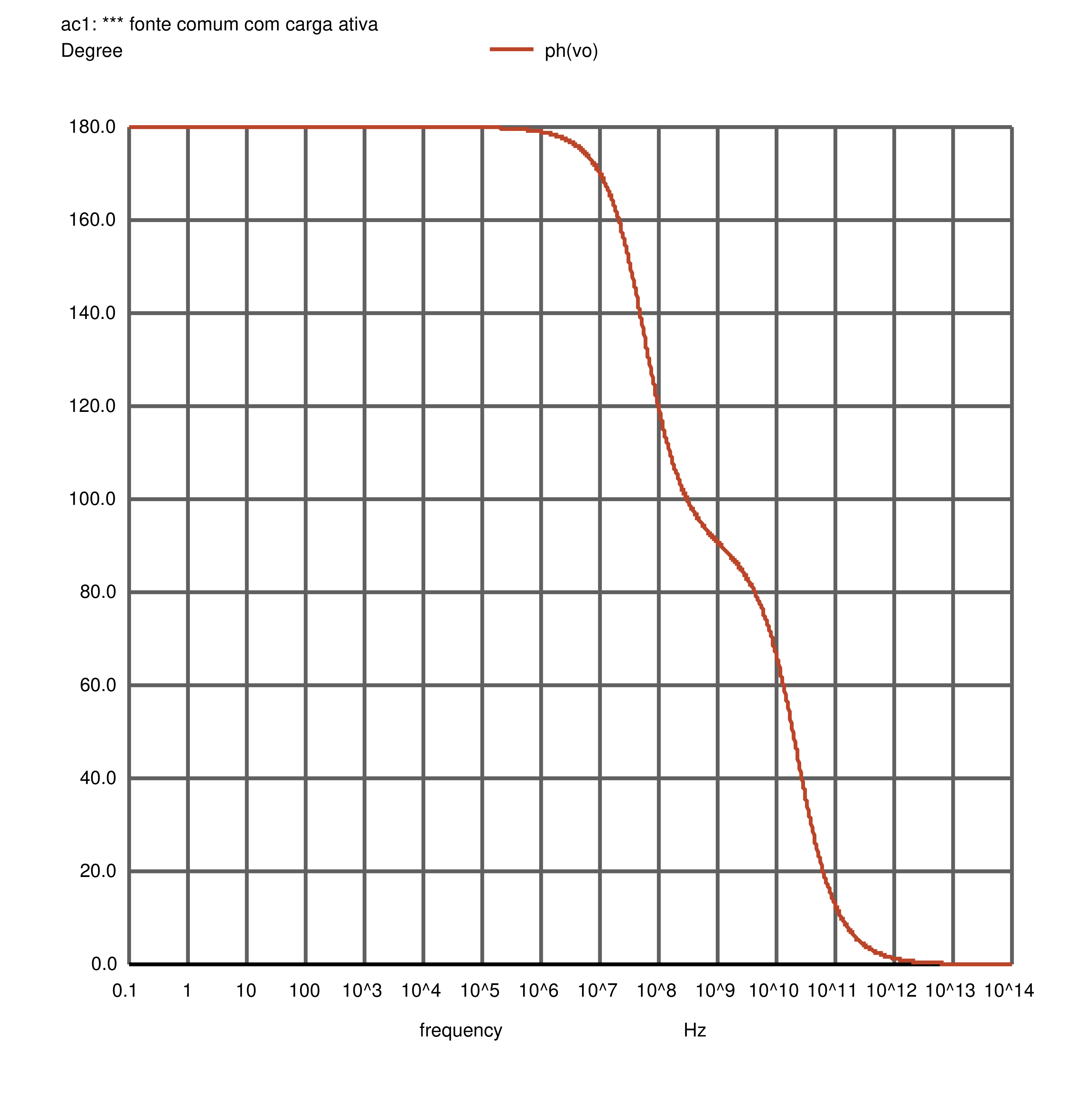
Figura 2.39: Fonte comum: fase da resposta em frequência, resultado da simulação AC. Sem \(R_{sig}\).

Os parâmetros exibidos na Figura 2.37 foram usados para calcular a função de transferência da Equação (2.8) através do Octave e o diagrama de Bode foi traçado, cujo resultado pode ser visto na Figura 2.40.

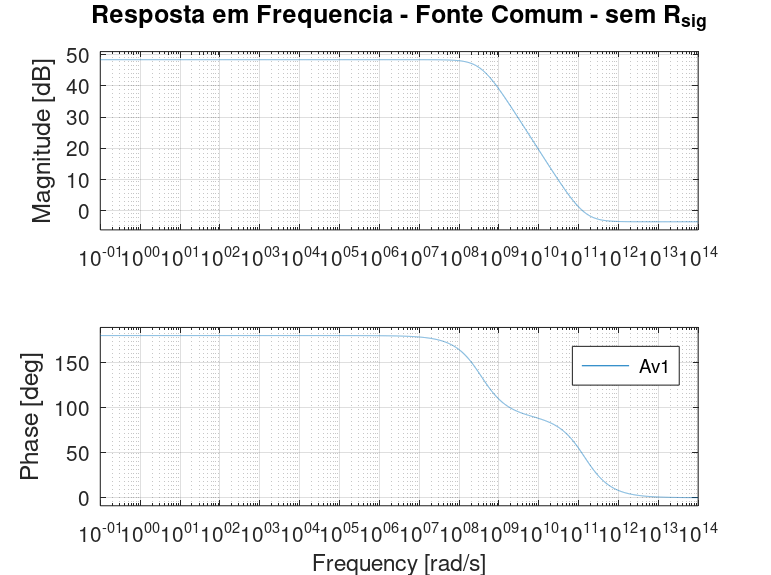
Figura 2.40: Fonte comum: diagrama de Bode calculado no Octave. Sem \(R_{sig}\).

Pode-se reparar como os resultados são visualmente muito parecidos. Para não ficar numa conferência visual, tanto o código NGSpice, quanto o código Octave trazem os cálculos dos parâmetros de interesse já listados. A Tabela 2.1 contém o resumo da comparação entre a simulação e o cálculo manual através da função de transferência. A coluna “Diferença” foi calculada tomando-se o valor da simulação como referência, uma vez que o simulador consegue pegar todas as não linearidades inerentes ao modelo original de simulação do transistor. Importante lembrar que as equações estabelecidas pelo modelo refletem dispositivos reais fabricados numa determinada tecnologia.

Tabela 2.1: Fonte Comum - NGSpice vs Octave - Sem \(R_{sig}\).

Parâmetro	NGSpice	Octave	Diferença (%)
Ganho CC	2.616509e+02	2.616510e+02	-0.00004
Ganho CC (dB)	4.835444e+01	4.835445e+01	-0.00001
\(f_{c}\) (Hz)	5.735938e+07	5.698111e+07	0.65947
\(f_u\) (Hz)	2.013806e+10	2.010205e+10	0.17880
Polo 1 (rad/s)	-3.603920e+08	-3.603915e+08	0.00013
Polo 2 (rad/s)	NA	NA	NA
Zero (rad/s)	1.414452e+11	1.414452e+11	0.00000

Percebe-se o quanto o modelo de pequenos sinais é uma boa aproximação para o comportamento do circuito. Contudo, também percebe-se que é difícil proceder com o cálculo da função de transferência sem que se conheça os valores dos parâmetros de pequenos sinais, que foram obtidos pela simulação, em cuja fidelidade estamos apostando. Logo, ainda que haja a dificuldade do cálculo para obtermos valores mais fidedignos de polos e zeros, por exemplo, podemos usar a função de transferência para entendermos qual a influência de cada parâmetro na resposta em frequência final do circuito. Em conjunto com a influência de cada parâmetro, podemos também estabelecer como a polarização irá afetar a resposta em frequência do circuito. Visto que boa parte das variáveis da função de transferência depdende da polarização e que essa interfere diferentemente em cada uma dessas variáveis, o efeito final pode também ser difícil de ser estudado. Nesse caso, uma análise de sensibilidade é um estudo complementar muito bom, mas não nos ateremos a ele aqui.

Para o caso da existência da resistência de fonte \(R_{sig}\), que é o caso real de todos os amplificadores, podemos ver a saída da simulação do NGSpice para o amplificador na Figura 2.41. O módulo da função de transferência pode ser visto na Figura 2.42 e a fase, na Figura 2.43.

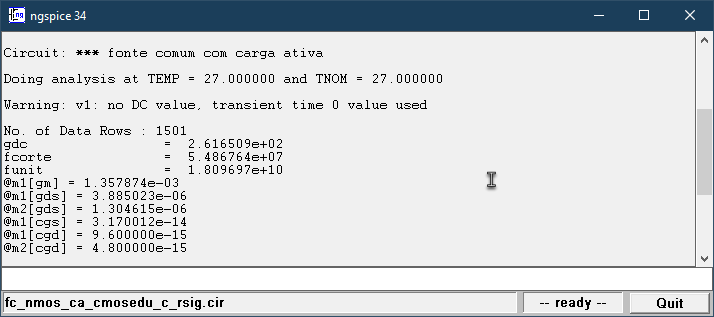
Figura 2.41: Fonte comum: log do NGSpice com resultados da simulação AC. Com \(R_{sig}\).

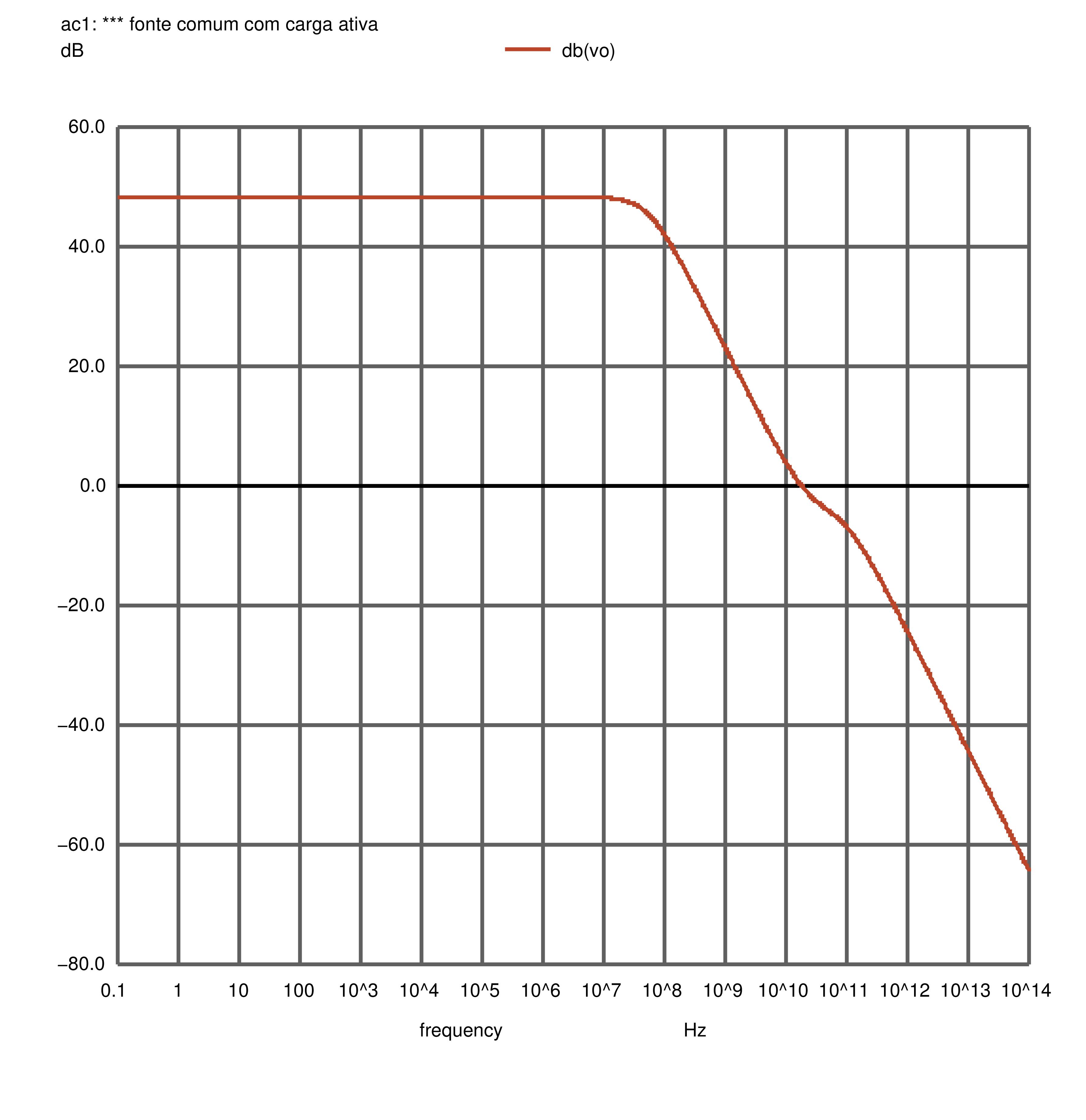
Figura 2.42: Fonte comum: módulo da resposta em frequência, resultado da simulação AC. Com \(R_{sig}\).

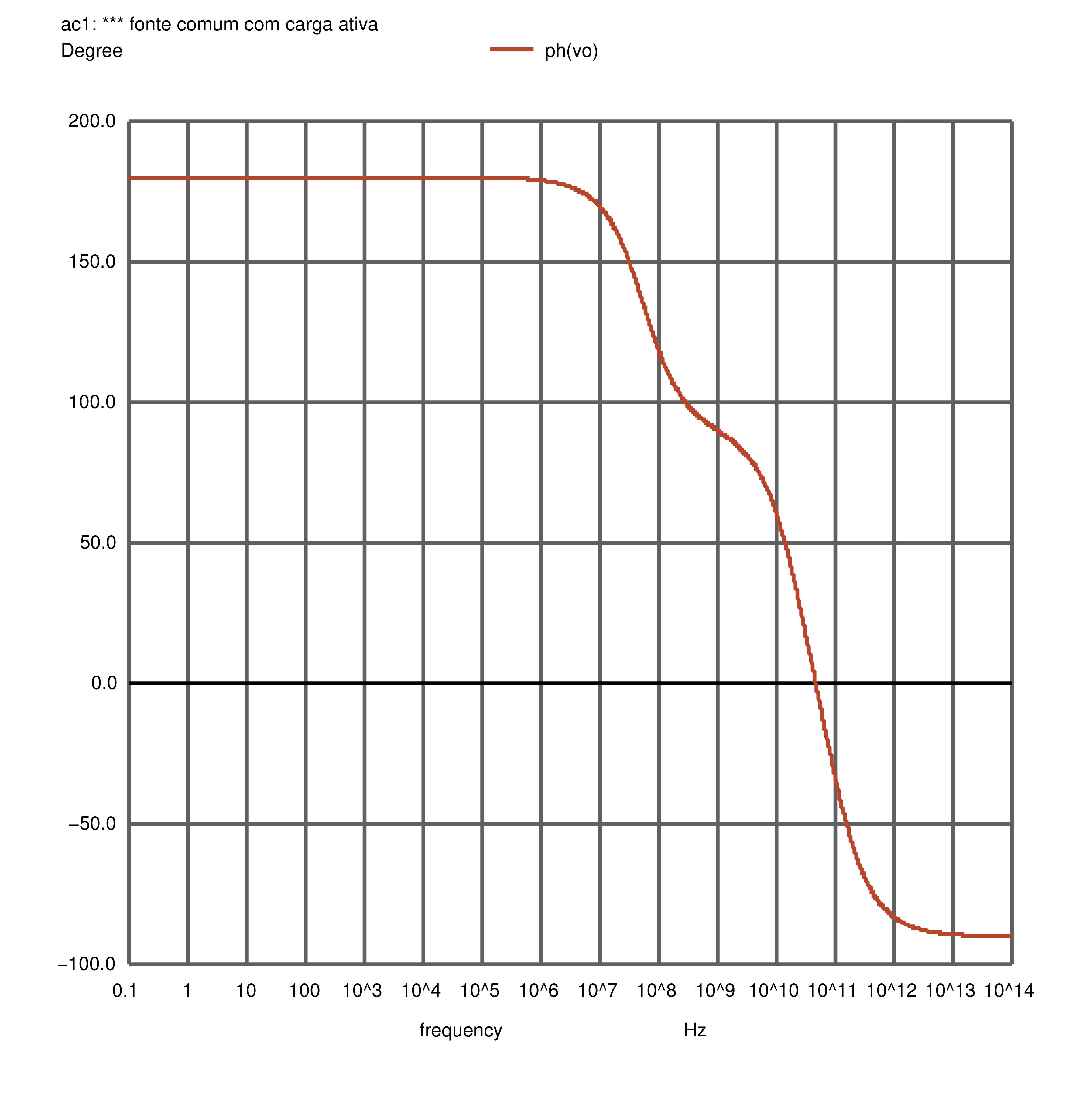
Figura 2.43: Fonte comum: fase da resposta em frequência, resultado da simulação AC. Com \(R_{sig}\).

Os parâmetros exibidos na Figura 2.37 foram usados para calcular a função de transferência da equação (2.10) através do Octave e o diagrama de Bode foi traçado, cujo resultado pode ser visto na Figura 2.44.

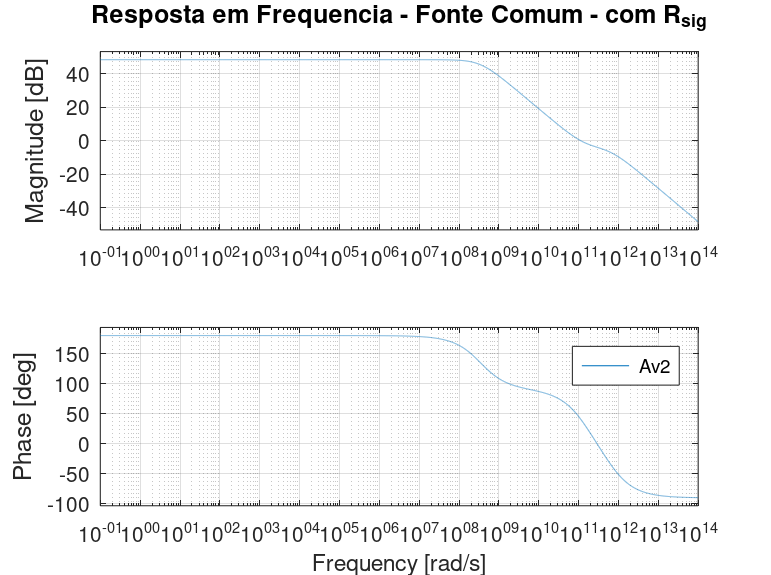
Figura 2.44: Fonte comum: diagrama de Bode calculado no Octave. Com \(R_{sig}\).

Tal como foi para o amplificador sem \(R_{sig}\), visualmente as respostas parecem iguais e, também como antes, uma comparação numérica se faz necessária. A Tabela 2.2 contém o resumo da comparação entre a simulação e o cálculo manual através da função de transferência.

Tabela 2.2: Fonte Comum - NGSpice vs Octave - Com \(R_{sig}\).

Parâmetro	NGSpice	Octave	Diferença (%)
Ganho CC	2.616509e+02	2.616510e+02	-0.00004
Ganho CC (dB)	4.835444e+01	4.835445e+01	-0.00001
\(f_{c}\) (Hz)	5.486764e+07	5.466726e+07	0.36520
\(f_u\) (Hz)	1.809697e+10	1.799827e+10	0.54538
Polo 1 (rad/s)	-3.447390e+08	-3.447386e+08	0.00011
Polo 2 (rad/s)	-5.983980e+11	-5.990840e+11	-0.11463
Zero (rad/s)	1.414452e+11	1.414452e+11	0.00000

Assim como antes, o comportamento do amplificador foi caracterizado da mesma forma por ambos os caminhos, sendo, contudo, necessária uma simulação do circuito no Spice para que se obtivesse os parâmetros de pequenos sinais. A confirmação do zero positivo foi feita, bem como o efeito de \(R_{sig}\) na influência clara de \(C_{gs_1}\) no acoplamento interno de entrada, gerado o segundo polo do amplificador.

A seguir tem-se os códigos para conferência. Você pode copiá-los, refazer as simulações e verificar o que aqui foi demonstrado, tendo a possiblidade de mudar detalhes, tal como o ponto de operação CC ou a temperatura do circuito, por exemplo.

2.3.6 Códigos para análise na frequência

Código de simulação (NGSpice) para o fonte comum, sem \(R_{sig}\)

*** Fonte Comum com carga ativa
*** Estudo da resposta em frequencia
*** Sem resistor de fonte
.global gnd vdd vss
.options savecurrents
.options filetype=ascii
.options wnflag=1
.options numdgt=14
.options measdgt=14

*** Circuito completo do Amplificador
** Transistor amplificador: nome dreno porta fonte corpo modelo L= W=
M1 vo vin gnd gnd N_1u L=0.6u W=48u
** Transistor de carga ativa
M2 vo vb vdd vdd P_1u L=2.4u W=24u ;L=1.0u W=12u

*** Definicao de parametros e inclusao de arquivos
.include "..\..\..\modelos\cmosedu_models.txt" ; precisa ser modificado para o seu computador
.param offset=0.794 ; flutuacao continua da senoide de entrada
.param amp=1m ; define a amplitude da senoide de entrada
.param vd=5 ;valor de Vdd
.param vb=3.444 ; polarizacao da carga ativa para ganho maximo

*** Definicao das fontes do circuito
** Fonte CC de alimentacao do circuito
vdd vdd gnd dc {vd}
** Fonte de sinal aplicada a entrada
v1 vin gnd sine ({offset} {amp} 10k) AC 1
** Fonte CC para polarizacao da carga ativa
vb vb gnd dc {vb}
.end

.control
set color0=white ; cor de fundo dos graficos = branco
set color1=black ; cor da grade dos graficos = preto
set units=degrees

*** Analise da resposta em frequencia do circuito
ac dec 100 0.1 100t
** Medicoes de interesse a partir a analise AC
meas ac gdc find vm(vo) at=0.1 ; mede o ganho em corrente continua
let gco = gdc/sqrt(2) ; mede o ganho na frequencia de corte: - 3dB
meas ac fcorte when vm(vo)=gco ; mede a frequencia de corte
meas ac funit when vm(vo)=1 ; mede a frequencia de ganho unitario

*** Impressao dos parametros de pequenos sinaisprint @m1[gm]
print @m1[gds]
print @m2[gds]
print @m1[cgs]
print @m1[cgd]
print @m2[cgd]

*** Visualizacao dos graficos de magnitude e fase
plot db(vo)
plot ph(vo)

*** Exportar os graficos para arquivo
set hcopypscolor=1 ; ajusta fundo branco para figuras salvas
* Salva em formato EPS os graficos gerados
* observe que apos nome do arquivo a chamada e identica
* a chamada anterior com o comando 'plot'
* O formato pode ser alterado para PostScript (.ps)
hardcopy fc_nmos_ca_resp_freq_s_rsig_mag.eps db(vo)
hardcopy fc_nmos_ca_resp_freq_s_rsig_fase.eps ph(vo)

*** Analise de polos e zeros vistos na transferencia entre
** saida (vo) e entrada (vi)
pz vin 0 vo 0 vol pz
** salva os resultados num arquivo .txt
print all > polos_zeros_s_rsig.txt

.endc

Código de simulação (NGSpice) para o fonte comum, com \(R_{sig}\)

*** Fonte Comum com carga ativa
*** Estudo da resposta em frequencia
*** Com resistor de fonte
.global gnd vdd vss
.options savecurrents
.options filetype=ascii
.options wnflag=1
.options numdgt=14
.options measdgt=14

*** Circuito completo do Amplificador
** Transistor amplificador: nome dreno porta fonte corpo modelo L= W=
M1 vo vin gnd gnd N_1u L=0.6u W=48u
** Transistor de carga ativa
M2 vo vb vdd vdd P_1u L=2.4u W=24u ;L=1.0u W=12u

*** Definicao de parametros e inclusao de arquivos
.include "..\..\..\modelos\cmosedu_models.txt" ; precisa ser modificado para o seu computador
.param offset=0.794 ; flutuacao continua da senoide de entrada
.param amp=1m ; define a amplitude da senoide de entrada
.param vd=5 ;valor de Vdd
.param vb=3.444 ; polarizacao da carga ativa para ganho maximo

*** Definicao das fontes do circuito
** Fonte CC de alimentacao do circuito
vdd vdd gnd dc {vd}
** Fonte de sinal aplicada a entrada com Rsig
v1 vi gnd sine ({offset} {amp} 10k) AC 1
r1 vi vin 50
** Fonte CC para polarizacao da carga ativa
vb vb gnd dc {vb}
.end

.control
set color0=white ; cor de fundo dos graficos = branco
set color1=black ; cor da grade dos graficos = preto
set units=degrees

*** Analise da resposta em frequencia do circuito
ac dec 100 0.1 100t
** Medicoes de interesse a partir a analise AC
meas ac gdc find vm(vo) at=0.1 ; mede o ganho em corrente continua
let gco = gdc/sqrt(2) ; mede o ganho na frequencia de corte: - 3dB
meas ac fcorte when vm(vo)=gco ; mede a frequencia de corte
meas ac funit when vm(vo)=1 ; mede a frequencia de ganho unitario

*** Impressao dos parametros de pequenos sinais
print @m1[gm]
print @m1[gds]
print @m2[gds]
print @m1[cgs]
print @m1[cgd]
print @m2[cgd]

*** Visualizacao dos graficos de magnitude e fase
plot db(vo)
plot ph(vo)

*** Exportar os graficos para arquivo
set hcopypscolor=1 ; ajusta fundo branco para figuras salvas
* Salva em formato EPS os graficos gerados
* observe que apos nome do arquivo a chamada e identica
* a chamada anterior com o comando 'plot'
* O formato pode ser alterado para PostScript (.ps)
hardcopy fc_nmos_ca_resp_freq_c_rsig_mag.eps db(vo)
hardcopy fc_nmos_ca_resp_freq_c_rsig_fase.eps ph(vo)

*** Analise de polos e zeros vistos na transferencia entre
** saida (vo) e entrada (vi)
pz vi 0 vo 0 vol pz
** salva os resultados num arquivo .txt
print all > polos_zeros_c_rsig.txt

.endc

Código de cálculo (Octave) para o fonte comum, sem \(R_{sig}\)

%%% Fonte Comum
%%% Calculo da funcao de transferencia - Sem Rsig
clear all
close all
clc
pkg load control
pkg load signal

%%% Definicao das variaveis vindas da simulacao
% resistencia da fonte de sinal
Rsig=50;
% transcondutancia
gm=1.357874e-03;
% resistencia de saida M1
ro1=1/3.885023e-06;
% resistencia de saida M2
ro2=1/1.304615e-06;
% resistencia de saida 
Ro=ro1*ro2/(ro1+ro2);
%% Capacitancias dos transistores
Cgs1=3.170012e-14;
Cgd1=9.600000e-15;
Cgd2=4.800000e-15;
Co=Cgd2;

%%% Funcao de transferencia sem Rsig
w = logspace(-1,14,5000);
num1 = [Ro*Cgd1 -gm*Ro];
den1 = [Ro*(Cgd1+Co) 1];
Av1 = tf(num1,den1);

%%% Calculo, Plotagem e Exportacao de resultados
figure(1);
bode(Av1,w); % calcula o bode do sistema e plota
[m1,f1]=bode(Av1,w); % calcula o bode e armazena os resulados
gcc=m1(1) % ganho em corrente continua
gccdb=20*log10(gcc)
gco=m1(1)/sqrt(2); % ganho na frequencia de corte
i_fc=lookup(m1,gco); % indice da frequencia de corte
wc=w(i_fc) % frequencia de corte, angular
fc=wc/2/pi % frequencia de corte, linear
i_fu=lookup(m1,1);
wu=w(i_fu) % frequencia de ganho unitario, angular
fu=wu/2/pi % frequencia de ganho unitario, linear
[z,p,k]=tf2zp(num1,den1)
h1=gcf; % armazena info da figura
ax = findall(h1,'type','axes'); % armazena os handles dos eixos 
title(ax(3), 'Resposta em Frequencia - Fonte Comum - sem R_{sig}'); % muda o titulo da figura
title_handle = get(ax(3),'title'); % armazena o handle do titulo do grafico
set(title_handle,'fontsize', 12); % ajusta a fonte do titulo
y1 = get(ax(3),'ylabel'); % armazena o handle do eixo de magnitude
set(y1,'fontsize', 12); % ajusta a fonte do eixo de magnitude
y2 = get(ax(2),'ylabel'); % armazena o handle do eixo de fase
set(y2,'fontsize', 12); % ajusta a fonte do eixo de fase
print -depsc fc_ca_verificacao_resp_freq_s_rsig.eps
print('color','fc_ca_verificacao_resp_freq_s_rsig.png'); % salva um PNG com o bode ajustado

Código de cálculo (Octave) para o fonte comum, com \(R_{sig}\)

%%% Fonte Comum
%%% Calculo da funcao de transferencia - Com Rsig
clear all
close all
clc
pkg load control
pkg load signal

%%% Definicao das variaveis vindas da simulacao
% resistencia da fonte de sinal
Rsig=50;
% transcondutancia
gm=1.357874e-03;
% resistencia de saida M1
ro1=1/3.885023e-06;
% resistencia de saida M2
ro2=1/1.304615e-06;
% resistencia de saida 
Ro=ro1*ro2/(ro1+ro2);
%% Capacitancias dos transistores
Cgs1=3.170012e-14;
Cgd1=9.600000e-15;
Cgd2=4.800000e-15;
Co=Cgd2;


%%% Funcao de transferencia com Rsig
w = logspace(-1,14,5000);
a = Ro*Rsig*(Cgd1*Cgs1+Cgd1*Co+Cgs1*Co);
b = Rsig*(Cgd1*(1+gm*Ro)+Cgs1)+Ro*(Cgd1+Co);
num2 = [Ro*Cgd1 -gm*Ro];
den2 = [a b 1];
Av2 = tf(num2,den2);

%%% Calculo, Plotagem e Exportacao de resultados
figure(1);
bode(Av2,w); % calcula o bode do sistema e plota
[m2,f2]=bode(Av2,w); % calcula o bode e armazena os resulados
gcc=m2(1) % ganho em corrente continua
gccdb=20*log10(gcc)
gco=m2(1)/sqrt(2); % ganho na frequencia de corte
i_fc=lookup(m2,gco); % indice da frequencia de corte
wc=w(i_fc) % frequencia de corte, angular
fc=wc/2/pi % frequencia de corte, linear
i_fu=lookup(m2,1);
wu=w(i_fu) % frequencia de ganho unitario, angular
fu=wu/2/pi % frequencia de ganho unitario, linear
[z,p,k]=tf2zp(num2,den2)
h1=gcf; % armazena info da figura
ax = findall(h1,'type','axes'); % armazena os handles dos eixos 
title(ax(3), 'Resposta em Frequencia - Fonte Comum - com R_{sig}'); % muda o titulo da figura
title_handle = get(ax(3),'title'); % armazena o handle do titulo do grafico
set(title_handle,'fontsize', 12); % ajusta a fonte do titulo
y1 = get(ax(3),'ylabel'); % armazena o handle do eixo de magnitude
set(y1,'fontsize', 12); % ajusta a fonte do eixo de magnitude
y2 = get(ax(2),'ylabel'); % armazena o handle do eixo de fase
set(y2,'fontsize', 12); % ajusta a fonte do eixo de fase
print -depsc fc_ca_verificacao_resp_freq_c_rsig.eps
print('color','fc_ca_verificacao_resp_freq_c_rsig.png'); % salva um PNG com o bode ajustado

2.3.7 Resumo do Fonte Comum

A Tabela 2.3 contém os principais resultados para o fonte comum que foram analisados ao longo dessa seção. Importante notar que as linhas Ganho, \(R_{in}\) ideal e \(R_{out}\) ideal contêm dois valores, cada uma. A de ganho refere-se ao ganho em tensão | corrente. As outras são para entrada e saía em: tensão | corrente, respectivamente. Essas linhas foram colocadas para facilitar a comparação do amplificador em estudo com as características ideais para entrada em tensão ou corrente.

É notório que a impedância de entrada infinita não favorece a utilização do fonte comum como um amplificador com entrada em corrente, já descartando-o para utilização como amplificador de corrente e de transimpedância. Contudo, está adequada para a entrada em tensão, ficando os amplificadores de tensão e de transadmitância favorecidos.

Por fim, percebe-se que a resistência de saída pode ser muito alta o que não favorece sua utilização como amplificador de tensão. Nesse caso um dos lados (entrada) está garantido, mas o outro não, de forma que essa configuração poderá ser usado como amplificador de tensão, apenas não será um excelente amplificador de tensão. Restando claro que, pela própria operação do transistor, o fonte comum é um excelente amplifcador de transadmitância.

Tabela 2.3: Tabela resumo do Fonte Comum.

Parâmetro	Fonte Comum
Ganho	\(-{g_{m}}({r_{o}}|| R_{A})\) (↑) | -
Fase	\(180^o\)
\(R_{in}\) ideal	\(\infty\) | \(0\)
\(R_{{in}}\)	\(\infty\)
\(R_{out}\) ideal	\(0\) | \(\infty\)
\(R_{{out}}\)	\({r_{o}}|| R_{A}\) (↑)

---

10. Página oficial do GNU Octave↩︎